2017河北中考数学3.3一次函数的实际应用教材知识梳理
文档属性
| 名称 | 2017河北中考数学3.3一次函数的实际应用教材知识梳理 |
|
|
| 格式 | zip | ||
| 文件大小 | 148.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-01-01 00:00:00 | ||
图片预览

文档简介
第三节 一次函数的实际应用
河北8年中考命题规律)
年份
题号
考查点
考查内容
分值
总分
2016
24
一次函数实际应用
以某商店玩具降价促销为素材考查一次函数的建模和应用,并与平均数相结合考查
10
10
2014
26探究(1)
一次函数实际应用
以某景区1号、2号两游览车的行驶路线为背景,探究(1)求一次函数的关系式,并求两车相距400
m时的时间
3
3
2012
24(1)
一次函数实际应用
以薄板为背景,(1)求出厂价与边长之间满足的一次函数关系式
2
2
2011
24(1)(2)
一次函数实际应用
以经销商每天用汽车和火车运货为背景,结合折线统计图,(1)求汽车和火车的速度;(2)求一次函数的关系式
5
5
2010
26(1)(4)
一次函数实际应用
以销售新型节能产品为背景:(1)由已知函数解析式求值;(4)求利润最大时的方案
6
6
2009
25
一次函数实际应用
以装修需要的板材为背景,(1)求表格中字母的值;(2)求满足关系的一次函数解析式;(3)求满足关系的一次函数解析式及不等式组的应用求最小值
12
12
命题规律
一次函数的实际应用在中考中一般设置一道题,分值为2—12分,均在解答题中考查,综合性较强,常考查型有:(1)一次函数解析式的实际应用,考查5次;(2)一次函数图象的实际应用,考查1次.
命题预测
预计2017年中考,一次函数的实际应用仍然为中考重点内容,题型多为解答题,主要训练掌握从实际问题中寻找等量关系的方法.
,河北8年中考真题及模拟)
INCLUDEPICTURE"命点.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/命点.TIF"
\
MERGEFORMAT
一次函数的实际应用(5次)
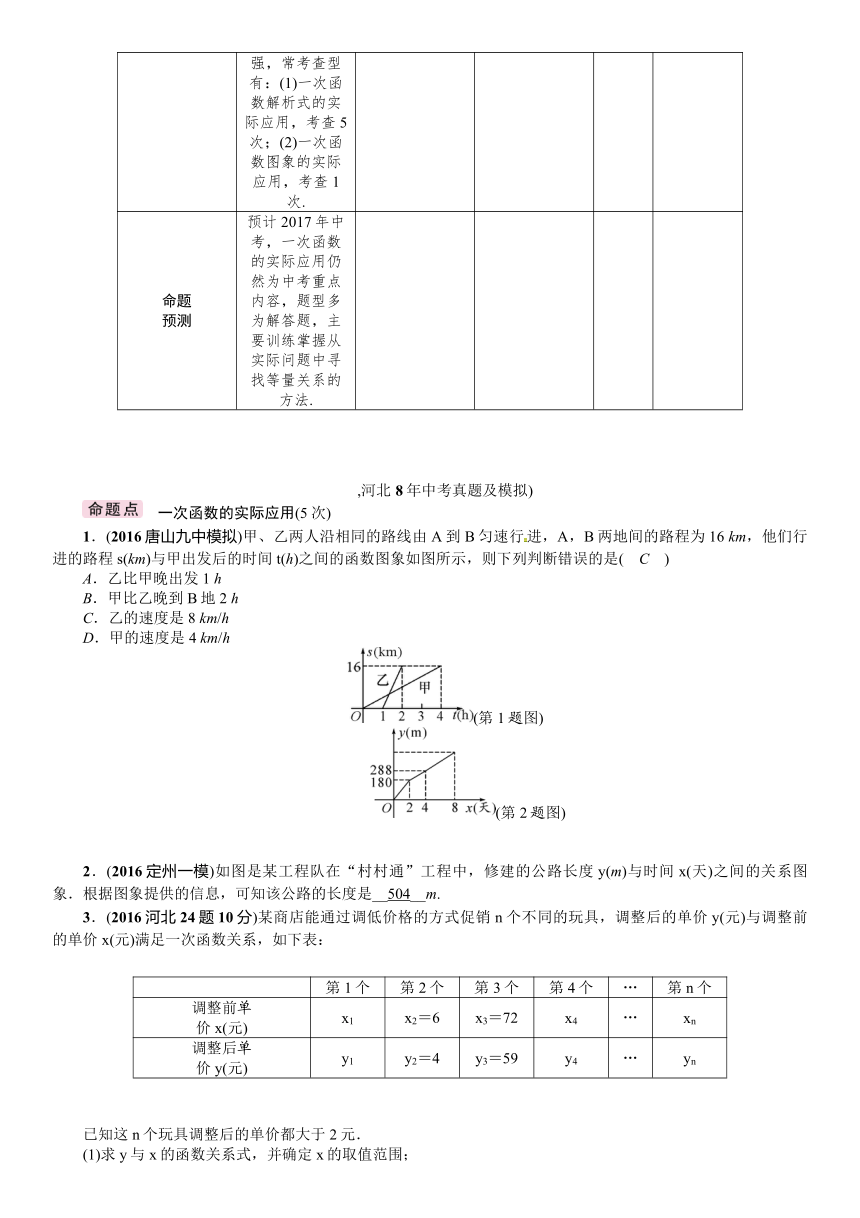
1.(2016唐山九中模拟)甲、乙两人沿相同的路线由A到B匀速行进,A,B两地间的路程为16
km,他们行进的路程s(km)与甲出发后的时间t(h)之间的函数图象如图所示,则下列判断错误的是( C )
A.乙比甲晚出发1
h
B.甲比乙晚到B地2
h
C.乙的速度是8
km/h
D.甲的速度是4
km/h
(第1题图)
(第2题图)
2.(2016定州一模)如图是某工程队在“村村通”工程中,修建的公路长度y(m)与时间x(天)之间的关系图象.根据图象提供的信息,可知该公路的长度是__504__m.
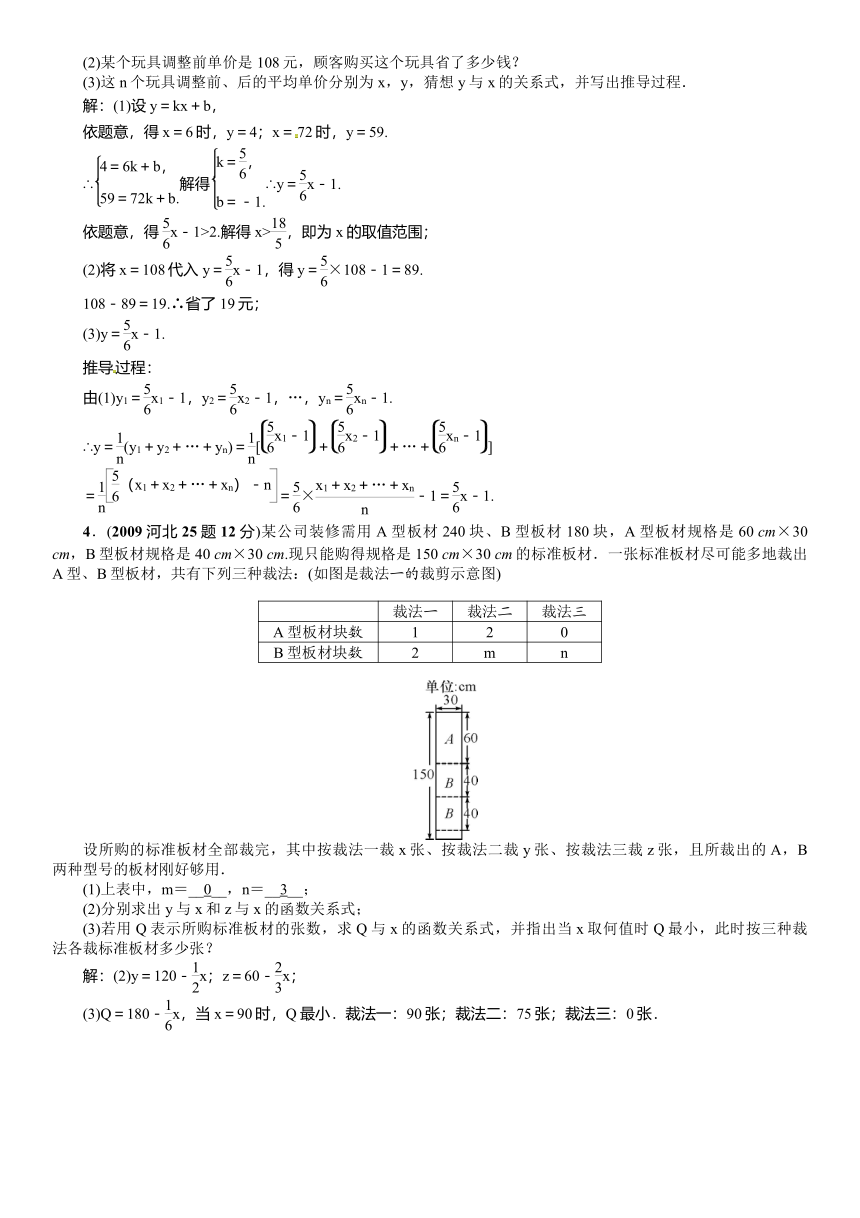
3.(2016河北24题10分)某商店能通过调低价格的方式促销n个不同的玩具,调整后的单价y(元)与调整前的单价x(元)满足一次函数关系,如下表:
第1个
第2个
第3个
第4个
…
第n个
调整前单价x(元)
x1
x2=6
x3=72
x4
…
xn
调整后单价y(元)
y1
y2=4
y3=59
y4
…
yn
已知这n个玩具调整后的单价都大于2元.
(1)求y与x的函数关系式,并确定x的取值范围;
(2)某个玩具调整前单价是108元,顾客购买这个玩具省了多少钱?
(3)这n个玩具调整前、后的平均单价分别为x,y,猜想y与x的关系式,并写出推导过程.
解:(1)设y=kx+b,
依题意,得x=6时,y=4;x=72时,y=59.
∴解得∴y=x-1.
依题意,得x-1>2.解得x>,即为x的取值范围;
(2)将x=108代入y=x-1,得y=×108-1=89.
108-89=19.∴省了19元;
(3)y=x-1.
推导过程:
由(1)y1=x1-1,y2=x2-1,…,yn=xn-1.
∴y=(y1+y2+…+yn)=[++…+]
==×-1=x-1.
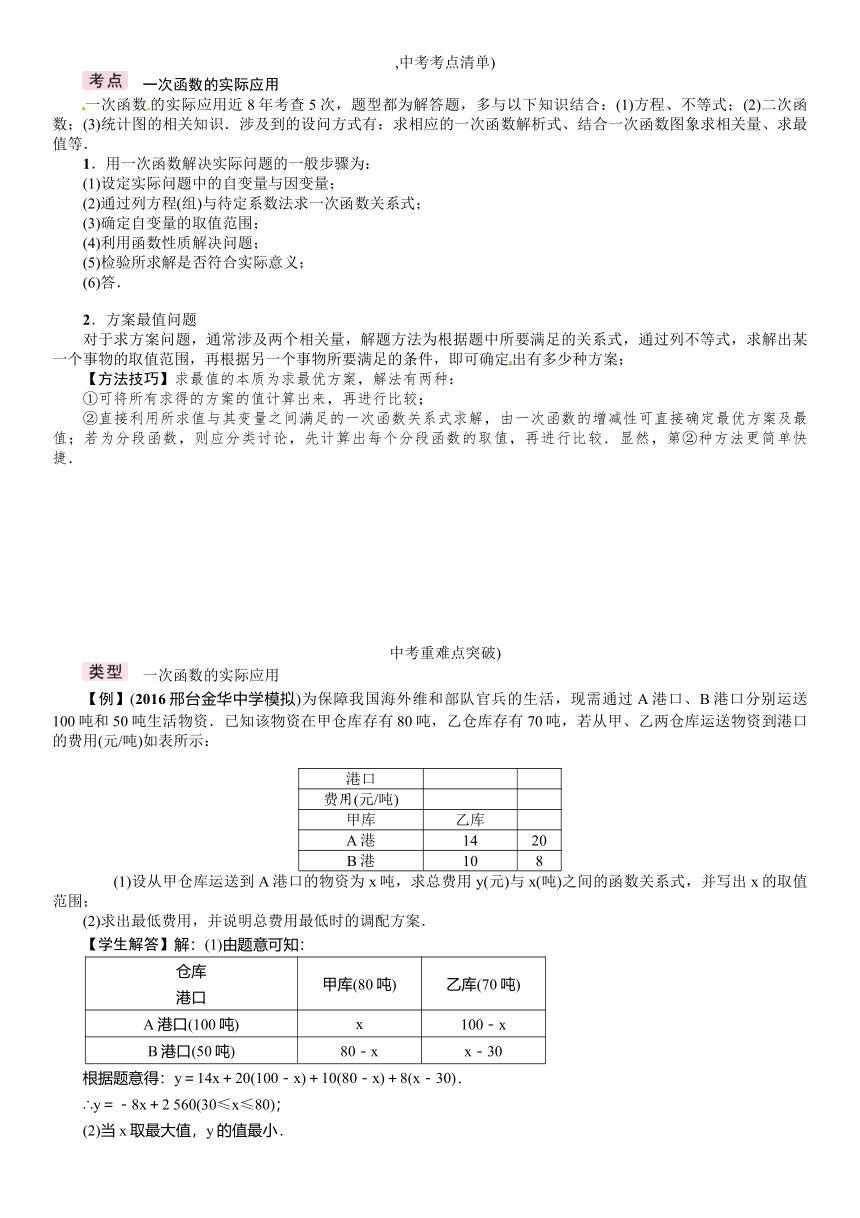
4.(2009河北25题12分)某公司装修需用A型板材240块、B型板材180块,A型板材规格是60
cm×30
cm,B型板材规格是40
cm×30
cm.现只能购得规格是150
cm×30
cm的标准板材.一张标准板材尽可能多地裁出A型、B型板材,共有下列三种裁法:(如图是裁法一的裁剪示意图)
裁法一
裁法二
裁法三
A型板材块数
1
2
0
B型板材块数
2
m
n
设所购的标准板材全部裁完,其中按裁法一裁x张、按裁法二裁y张、按裁法三裁z张,且所裁出的A,B两种型号的板材刚好够用.
(1)上表中,m=__0__,n=__3__;
(2)分别求出y与x和z与x的函数关系式;
(3)若用Q表示所购标准板材的张数,求Q与x的函数关系式,并指出当x取何值时Q最小,此时按三种裁法各裁标准板材多少张?
解:(2)y=120-x;z=60-x;
(3)Q=180-x,当x=90时,Q最小.裁法一:90张;裁法二:75张;裁法三:0张.
,中考考点清单)
INCLUDEPICTURE"考点.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/考点.TIF"
\
MERGEFORMAT
一次函数的实际应用
一次函数的实际应用近8年考查5次,题型都为解答题,多与以下知识结合:(1)方程、不等式;(2)二次函数;(3)统计图的相关知识.涉及到的设问方式有:求相应的一次函数解析式、结合一次函数图象求相关量、求最值等.
1.用一次函数解决实际问题的一般步骤为:
(1)设定实际问题中的自变量与因变量;
(2)通过列方程(组)与待定系数法求一次函数关系式;
(3)确定自变量的取值范围;
(4)利用函数性质解决问题;
(5)检验所求解是否符合实际意义;
(6)答.
2.方案最值问题
对于求方案问题,通常涉及两个相关量,解题方法为根据题中所要满足的关系式,通过列不等式,求解出某一个事物的取值范围,再根据另一个事物所要满足的条件,即可确定出有多少种方案;
【方法技巧】求最值的本质为求最优方案,解法有两种:
①可将所有求得的方案的值计算出来,再进行比较;
②直接利用所求值与其变量之间满足的一次函数关系式求解,由一次函数的增减性可直接确定最优方案及最值;若为分段函数,则应分类讨论,先计算出每个分段函数的取值,再进行比较.显然,第②种方法更简单快捷.
中考重难点突破)
INCLUDEPICTURE"类型.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/类型.TIF"
\
MERGEFORMAT
一次函数的实际应用
【例】(2016邢台金华中学模拟)为保障我国海外维和部队官兵的生活,现需通过A港口、B港口分别运送100吨和50吨生活物资.已知该物资在甲仓库存有80吨,乙仓库存有70吨,若从甲、乙两仓库运送物资到港口的费用(元/吨)如表所示:
港口
费用(元/吨)
甲库
乙库
A港
14
20
B港
10
8
(1)设从甲仓库运送到A港口的物资为x吨,求总费用y(元)与x(吨)之间的函数关系式,并写出x的取值范围;
(2)求出最低费用,并说明总费用最低时的调配方案.
【学生解答】解:(1)由题意可知:
仓库港口
甲库(80吨)
乙库(70吨)
A港口(100吨)
x
100-x
B港口(50吨)
80-x
x-30
根据题意得:y=14x+20(100-x)+10(80-x)+8(x-30).
∴y=-8x+2
560(30≤x≤80);
(2)当x取最大值,y的值最小.
∴当x=80时,y=-8×80+2
560=1
920.
∴从甲仓库运80吨物资到A港口;乙仓库运20吨物资到A港口,运50吨物资到B港口时,总费用最低.
INCLUDEPICTURE"针对.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/针对.TIF"
\
MERGEFORMAT
1.(2016孝感中考)孝感市在创建国家级园林城市中,绿化档次不断提升.某校计划购进A,B两种树木共100棵进行校园绿化升级.经市场调查:购买A种树木2棵,B种树木5棵,共需600元;购买A种树木3棵,B种树木1棵,共需380元.
(1)求A种,B种树木每棵各多少元?
(2)因布局需要,购买A种树木的数量不少于B种树木数量的3倍.学校与中标公司签订的合同中规定:在市场价格不变的情况下(不考虑其他因素),实际付款总金额按市场价九折优惠.请设计一种购买树木的方案,使实际所花费用最省,并求出最省的费用.
解:(1)A种,B种树木每棵分别为100元,80元;
(2)设购买A种树木为x棵,则购买B种树木为(100-x)棵,
则x≥3(100-x),∴x≥75.
设实际付款总金额为y元,则y=0.9[100x+80(100-x)],
y=18x+7
200.
∵18>0,y随x的增大而增大,∴x=75时,y最小.
即x=75,y最小值=18×75+7
200=8
550(元).
∴当购买A种树木75棵,B种树木25棵时,所需费用最少,最少费用为8
550元.
2.(2016原创)张家口市某学校开展“青少年科技创新比赛”活动,“喜洋洋”代表队设计了一个遥控车沿直线轨道AC做匀速直线运动的模型.甲、乙两车同时分别从A,B出发,沿轨道到达C处,B在AC上,甲的速度是乙的速度的1.5倍,设t
min后甲、乙两遥控车与B处的距离分别为d1,d2,则d1,d2与t的函数关系如图,试根据图象解决下列问题:
(1)填空:乙的速度v2=__40__m/min;
(2)写出d1与t的函数关系式;
(3)若甲、乙两遥控车的距离超过10
m时信号不会产生相互干扰,试探求什么时间两遥控车的信号不会产生相互干扰?
解:(2)d1=;(3)0≤t<时,两遥控车的信号不会产生相互干扰.
,中考备考方略)
INCLUDEPICTURE"基础训练.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/基础训练.TIF"
\
MERGEFORMAT
1.(2016临沂中考)甲、乙两辆摩托车同时从相距20
km的A,B两地出发,相向而行.图中l1,l2分别表示甲、乙两辆摩托车到A地的距离s(km)与行驶时间t(h)的函数关系,则下列说法错误的是( C )
A.乙摩托车的速度较快
B.经过0.3
h甲摩托车行驶到A,B两地的中点
C.经过0.25
h两摩托车相遇
D.当乙摩托车到达A地时,甲摩托车距离A地
km
2.(2016湖州中考)放学后,小明骑车回家,他经过的路程s(km)与所用时间t(min)的函数关系如图所示,则小明的骑车速度是__0.2__km/min.
(第2题图)
(第3题图)
3.(2016绍兴中考)根据卫生防疫部门要求,游泳池必须定期换水、清洗.某游泳池周五早上8:00打开排水孔开始排水,排水孔的排水速度保持不变,期间因清洗游泳池需要暂停排水,游泳池的水在11:30全部排完.游泳池内的水量Q(m3)和开始排水后的时间t(h)之间的函数图象如图所示,根据图象解答下列问题:
(1)暂停排水需要多少时间?排水孔的排水速度是多少?
(2)当2≤t≤3.5时,求Q关于t的函数解析式.
解:(1)暂停排水时间为30
min(半小时);
排水孔的排水速度为300
m3/h;
(2)设当2≤t≤3.5时,Q关于t的函数解析式为Q=kt+b,把(2,450),(3.5,0)代入得解得
∴函数解析式为Q=-300t+1
050.
4.(2016天津中考)公司有330台机器需要一次性运送到某地,计划租用甲、乙两种货车共8辆.已知每辆甲种货车一次最多运送机器45台、租车费用为400元,每辆乙种货车一次最多运送机器30台、租车费用为280元.
(1)设租用甲种货车x辆(x为非负整数),试填写下表.
表一:
租用甲种货车的数量/辆
3
7
x
租用的甲种货车最多运送机器的数量/台
135
租用的乙种货车最多运送机器的数量/台
150
表二:
租用甲种货车的数量/辆
3
7
x
租用甲种货车的费用/元
2
800
租用乙种货车的费用/元
280
(2)给出能完成此项运动任务的最节省费用的租车方案,并说明理由.
解:(1)表一:315,45x,30,-30x+240;
表二:1
200,400x,1
400,-280x+2
240;
(2)租用甲种货车x辆时,两种货车的总费用为y=400x+(-280x+2
240)=120x+2
240,
其中45x+(-30x+240)≥330,解得x≥6.
∵120>0,∴y随x的增大而增大.
∴当x=6时,y取得最小值.
答:能完成此项运送任务的最节省费用的租车方案为甲种货车6辆,乙种货车2辆.
INCLUDEPICTURE"能力提升.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/能力提升.TIF"
\
MERGEFORMAT
5.(2016济宁中考)小明到服装店参加社会实践活动,服装店经理让小明帮助解决以下问题:
服装店准备购进甲乙两种服装,甲种每件进价80元,售价120元;乙种每件进价60元,售价90元,计划购进两种服装共100件,其中甲种服装不少于65件.
(1)若购进这100件服装的费用不得超过7
500,则甲种服装最多购进多少件?
(2)在(1)条件下,该服装店在6月21日父亲节当天对甲种服装以每件优惠a(0解:(1)设购进甲种服装x件,由题意得80x+60(100-x)≤7
500.解得x≤75.
答:甲种服装最多购进75件;
(2)设总利润为w元,因为甲种服装不少于65件,所以65≤x≤75.
则w=(40-a)x+30(100-x)=(10-a)x+3
000.
当00,w随x的增大而增大,
所以当x=75时,w有最大值,则购进甲种服装75件,乙种服装25件;
当a=10时,所有方案获利相同,所以按哪种方案进货都可以(甲种服装进货量在65~75件之间);
当10所以当x=65时,w有最大值,则购进甲种服装65件,乙种服装35件.
6.(2016丽水中考)2016年3月27日“丽水半程马拉松竞赛”在莲都举行,某运动员从起点万地广场西门出发,途径紫金大桥,沿比赛路线跑回终点万地广场西门.设该运动员离开起点的路程s(km)与跑步时间t(min)之间的函数关系如图所示.其中从起点到紫金大桥的平均速度是0.3
km/min.用时35
min,根据图象提供的信息,解答下列问题:
(1)求图中a的值;
(2)组委会在距离起点2.1
km处设立一个拍摄点C,该运动员从第一次过点C到第二次过点C所用的时间为68
min.
①求AB所在直线的函数解析式;
②该运动员跑完赛程用时多少分钟?
解:(1)∵从起点到紫金大桥的平均速度是0.3
km/min,用时35
min.
∴a=0.3×35=10.5(km);
(2)①∵线段OA经过点O(0,0),A(35,10.5),∴OA的函数解析式是s=0.3t(0≤t≤35).
∴当s=2.1时,0.3t=2.1,解得t=7.
∴该运动员从第一次过C点到第二次过C点所用的时间为68
min.
∴该运动员从起点到第二次过C点共用的时间是7+68=75(min).
∴AB经过(35,10.5),(75,2.1)两点.
设AB所在直线的函数解析式是s=kt+b.
∴解得
∴AB所在直线的函数解析式是s=-0.21t+17.85;
②∵该运动员跑完赛程所用的时间即为直线AB与x轴交点横坐标的值.
∴当s=0时,-0.21t+17.85=0,解得t=85.
∴该运动员跑完赛程用时85
min.
7.(2016包头中考)我市某养殖场计划购买甲、乙两种鱼苗共700尾,甲种鱼苗每尾3元,乙种鱼苗每尾5元,相关资料表明:甲、乙两种鱼苗的成活率分别为85%和90%.
(1)若购买这两种鱼苗共用去2
500元,则甲、乙两种鱼苗各购买多少尾?
(2)若要使这批鱼苗的总成活率不低于88%,则甲种鱼苗至多购买多少尾?
(3)在(2)的条件下,应如何选购鱼苗,使购买鱼苗的费用最低?并求出最低费用.
解:(1)设购买甲种鱼苗x尾,乙种鱼苗y尾,根据题意可得:解得
答:购买甲种鱼苗500尾,乙种鱼苗200尾;
(2)设购买甲种鱼苗z尾,乙种鱼苗(700-z)尾,列不等式得:85%z+90%(700-z)≥700×88%,解得z≤280.
答:甲种鱼苗至多购买280尾;
(3)设甲种鱼苗购买m尾,购买鱼苗的费用为w元,则w=3m+5(700-m)=-2m+3
500,
∵-2<0,∴w随m的增大而减小.
∵0500-2×280=2
940(元).
∴700-m=420.
答:当选购甲种鱼苗280尾,乙种鱼苗420尾时,总费用最低,最低费用为2
940元.
河北8年中考命题规律)
年份
题号
考查点
考查内容
分值
总分
2016
24
一次函数实际应用
以某商店玩具降价促销为素材考查一次函数的建模和应用,并与平均数相结合考查
10
10
2014
26探究(1)
一次函数实际应用
以某景区1号、2号两游览车的行驶路线为背景,探究(1)求一次函数的关系式,并求两车相距400
m时的时间
3
3
2012
24(1)
一次函数实际应用
以薄板为背景,(1)求出厂价与边长之间满足的一次函数关系式
2
2
2011
24(1)(2)
一次函数实际应用
以经销商每天用汽车和火车运货为背景,结合折线统计图,(1)求汽车和火车的速度;(2)求一次函数的关系式
5
5
2010
26(1)(4)
一次函数实际应用
以销售新型节能产品为背景:(1)由已知函数解析式求值;(4)求利润最大时的方案
6
6
2009
25
一次函数实际应用
以装修需要的板材为背景,(1)求表格中字母的值;(2)求满足关系的一次函数解析式;(3)求满足关系的一次函数解析式及不等式组的应用求最小值
12
12
命题规律
一次函数的实际应用在中考中一般设置一道题,分值为2—12分,均在解答题中考查,综合性较强,常考查型有:(1)一次函数解析式的实际应用,考查5次;(2)一次函数图象的实际应用,考查1次.
命题预测
预计2017年中考,一次函数的实际应用仍然为中考重点内容,题型多为解答题,主要训练掌握从实际问题中寻找等量关系的方法.
,河北8年中考真题及模拟)
INCLUDEPICTURE"命点.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/命点.TIF"
\
MERGEFORMAT
一次函数的实际应用(5次)
1.(2016唐山九中模拟)甲、乙两人沿相同的路线由A到B匀速行进,A,B两地间的路程为16
km,他们行进的路程s(km)与甲出发后的时间t(h)之间的函数图象如图所示,则下列判断错误的是( C )
A.乙比甲晚出发1
h
B.甲比乙晚到B地2
h
C.乙的速度是8
km/h
D.甲的速度是4
km/h
(第1题图)
(第2题图)
2.(2016定州一模)如图是某工程队在“村村通”工程中,修建的公路长度y(m)与时间x(天)之间的关系图象.根据图象提供的信息,可知该公路的长度是__504__m.
3.(2016河北24题10分)某商店能通过调低价格的方式促销n个不同的玩具,调整后的单价y(元)与调整前的单价x(元)满足一次函数关系,如下表:
第1个
第2个
第3个
第4个
…
第n个
调整前单价x(元)
x1
x2=6
x3=72
x4
…
xn
调整后单价y(元)
y1
y2=4
y3=59
y4
…
yn
已知这n个玩具调整后的单价都大于2元.
(1)求y与x的函数关系式,并确定x的取值范围;
(2)某个玩具调整前单价是108元,顾客购买这个玩具省了多少钱?
(3)这n个玩具调整前、后的平均单价分别为x,y,猜想y与x的关系式,并写出推导过程.
解:(1)设y=kx+b,
依题意,得x=6时,y=4;x=72时,y=59.
∴解得∴y=x-1.
依题意,得x-1>2.解得x>,即为x的取值范围;
(2)将x=108代入y=x-1,得y=×108-1=89.
108-89=19.∴省了19元;
(3)y=x-1.
推导过程:
由(1)y1=x1-1,y2=x2-1,…,yn=xn-1.
∴y=(y1+y2+…+yn)=[++…+]
==×-1=x-1.
4.(2009河北25题12分)某公司装修需用A型板材240块、B型板材180块,A型板材规格是60
cm×30
cm,B型板材规格是40
cm×30
cm.现只能购得规格是150
cm×30
cm的标准板材.一张标准板材尽可能多地裁出A型、B型板材,共有下列三种裁法:(如图是裁法一的裁剪示意图)
裁法一
裁法二
裁法三
A型板材块数
1
2
0
B型板材块数
2
m
n
设所购的标准板材全部裁完,其中按裁法一裁x张、按裁法二裁y张、按裁法三裁z张,且所裁出的A,B两种型号的板材刚好够用.
(1)上表中,m=__0__,n=__3__;
(2)分别求出y与x和z与x的函数关系式;
(3)若用Q表示所购标准板材的张数,求Q与x的函数关系式,并指出当x取何值时Q最小,此时按三种裁法各裁标准板材多少张?
解:(2)y=120-x;z=60-x;
(3)Q=180-x,当x=90时,Q最小.裁法一:90张;裁法二:75张;裁法三:0张.
,中考考点清单)
INCLUDEPICTURE"考点.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/考点.TIF"
\
MERGEFORMAT
一次函数的实际应用
一次函数的实际应用近8年考查5次,题型都为解答题,多与以下知识结合:(1)方程、不等式;(2)二次函数;(3)统计图的相关知识.涉及到的设问方式有:求相应的一次函数解析式、结合一次函数图象求相关量、求最值等.
1.用一次函数解决实际问题的一般步骤为:
(1)设定实际问题中的自变量与因变量;
(2)通过列方程(组)与待定系数法求一次函数关系式;
(3)确定自变量的取值范围;
(4)利用函数性质解决问题;
(5)检验所求解是否符合实际意义;
(6)答.
2.方案最值问题
对于求方案问题,通常涉及两个相关量,解题方法为根据题中所要满足的关系式,通过列不等式,求解出某一个事物的取值范围,再根据另一个事物所要满足的条件,即可确定出有多少种方案;
【方法技巧】求最值的本质为求最优方案,解法有两种:
①可将所有求得的方案的值计算出来,再进行比较;
②直接利用所求值与其变量之间满足的一次函数关系式求解,由一次函数的增减性可直接确定最优方案及最值;若为分段函数,则应分类讨论,先计算出每个分段函数的取值,再进行比较.显然,第②种方法更简单快捷.
中考重难点突破)
INCLUDEPICTURE"类型.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/类型.TIF"
\
MERGEFORMAT
一次函数的实际应用
【例】(2016邢台金华中学模拟)为保障我国海外维和部队官兵的生活,现需通过A港口、B港口分别运送100吨和50吨生活物资.已知该物资在甲仓库存有80吨,乙仓库存有70吨,若从甲、乙两仓库运送物资到港口的费用(元/吨)如表所示:
港口
费用(元/吨)
甲库
乙库
A港
14
20
B港
10
8
(1)设从甲仓库运送到A港口的物资为x吨,求总费用y(元)与x(吨)之间的函数关系式,并写出x的取值范围;
(2)求出最低费用,并说明总费用最低时的调配方案.
【学生解答】解:(1)由题意可知:
仓库港口
甲库(80吨)
乙库(70吨)
A港口(100吨)
x
100-x
B港口(50吨)
80-x
x-30
根据题意得:y=14x+20(100-x)+10(80-x)+8(x-30).
∴y=-8x+2
560(30≤x≤80);
(2)当x取最大值,y的值最小.
∴当x=80时,y=-8×80+2
560=1
920.
∴从甲仓库运80吨物资到A港口;乙仓库运20吨物资到A港口,运50吨物资到B港口时,总费用最低.
INCLUDEPICTURE"针对.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/针对.TIF"
\
MERGEFORMAT
1.(2016孝感中考)孝感市在创建国家级园林城市中,绿化档次不断提升.某校计划购进A,B两种树木共100棵进行校园绿化升级.经市场调查:购买A种树木2棵,B种树木5棵,共需600元;购买A种树木3棵,B种树木1棵,共需380元.
(1)求A种,B种树木每棵各多少元?
(2)因布局需要,购买A种树木的数量不少于B种树木数量的3倍.学校与中标公司签订的合同中规定:在市场价格不变的情况下(不考虑其他因素),实际付款总金额按市场价九折优惠.请设计一种购买树木的方案,使实际所花费用最省,并求出最省的费用.
解:(1)A种,B种树木每棵分别为100元,80元;
(2)设购买A种树木为x棵,则购买B种树木为(100-x)棵,
则x≥3(100-x),∴x≥75.
设实际付款总金额为y元,则y=0.9[100x+80(100-x)],
y=18x+7
200.
∵18>0,y随x的增大而增大,∴x=75时,y最小.
即x=75,y最小值=18×75+7
200=8
550(元).
∴当购买A种树木75棵,B种树木25棵时,所需费用最少,最少费用为8
550元.
2.(2016原创)张家口市某学校开展“青少年科技创新比赛”活动,“喜洋洋”代表队设计了一个遥控车沿直线轨道AC做匀速直线运动的模型.甲、乙两车同时分别从A,B出发,沿轨道到达C处,B在AC上,甲的速度是乙的速度的1.5倍,设t
min后甲、乙两遥控车与B处的距离分别为d1,d2,则d1,d2与t的函数关系如图,试根据图象解决下列问题:
(1)填空:乙的速度v2=__40__m/min;
(2)写出d1与t的函数关系式;
(3)若甲、乙两遥控车的距离超过10
m时信号不会产生相互干扰,试探求什么时间两遥控车的信号不会产生相互干扰?
解:(2)d1=;(3)0≤t<时,两遥控车的信号不会产生相互干扰.
,中考备考方略)
INCLUDEPICTURE"基础训练.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/基础训练.TIF"
\
MERGEFORMAT
1.(2016临沂中考)甲、乙两辆摩托车同时从相距20
km的A,B两地出发,相向而行.图中l1,l2分别表示甲、乙两辆摩托车到A地的距离s(km)与行驶时间t(h)的函数关系,则下列说法错误的是( C )
A.乙摩托车的速度较快
B.经过0.3
h甲摩托车行驶到A,B两地的中点
C.经过0.25
h两摩托车相遇
D.当乙摩托车到达A地时,甲摩托车距离A地
km
2.(2016湖州中考)放学后,小明骑车回家,他经过的路程s(km)与所用时间t(min)的函数关系如图所示,则小明的骑车速度是__0.2__km/min.
(第2题图)
(第3题图)
3.(2016绍兴中考)根据卫生防疫部门要求,游泳池必须定期换水、清洗.某游泳池周五早上8:00打开排水孔开始排水,排水孔的排水速度保持不变,期间因清洗游泳池需要暂停排水,游泳池的水在11:30全部排完.游泳池内的水量Q(m3)和开始排水后的时间t(h)之间的函数图象如图所示,根据图象解答下列问题:
(1)暂停排水需要多少时间?排水孔的排水速度是多少?
(2)当2≤t≤3.5时,求Q关于t的函数解析式.
解:(1)暂停排水时间为30
min(半小时);
排水孔的排水速度为300
m3/h;
(2)设当2≤t≤3.5时,Q关于t的函数解析式为Q=kt+b,把(2,450),(3.5,0)代入得解得
∴函数解析式为Q=-300t+1
050.
4.(2016天津中考)公司有330台机器需要一次性运送到某地,计划租用甲、乙两种货车共8辆.已知每辆甲种货车一次最多运送机器45台、租车费用为400元,每辆乙种货车一次最多运送机器30台、租车费用为280元.
(1)设租用甲种货车x辆(x为非负整数),试填写下表.
表一:
租用甲种货车的数量/辆
3
7
x
租用的甲种货车最多运送机器的数量/台
135
租用的乙种货车最多运送机器的数量/台
150
表二:
租用甲种货车的数量/辆
3
7
x
租用甲种货车的费用/元
2
800
租用乙种货车的费用/元
280
(2)给出能完成此项运动任务的最节省费用的租车方案,并说明理由.
解:(1)表一:315,45x,30,-30x+240;
表二:1
200,400x,1
400,-280x+2
240;
(2)租用甲种货车x辆时,两种货车的总费用为y=400x+(-280x+2
240)=120x+2
240,
其中45x+(-30x+240)≥330,解得x≥6.
∵120>0,∴y随x的增大而增大.
∴当x=6时,y取得最小值.
答:能完成此项运送任务的最节省费用的租车方案为甲种货车6辆,乙种货车2辆.
INCLUDEPICTURE"能力提升.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/能力提升.TIF"
\
MERGEFORMAT
5.(2016济宁中考)小明到服装店参加社会实践活动,服装店经理让小明帮助解决以下问题:
服装店准备购进甲乙两种服装,甲种每件进价80元,售价120元;乙种每件进价60元,售价90元,计划购进两种服装共100件,其中甲种服装不少于65件.
(1)若购进这100件服装的费用不得超过7
500,则甲种服装最多购进多少件?
(2)在(1)条件下,该服装店在6月21日父亲节当天对甲种服装以每件优惠a(0
500.解得x≤75.
答:甲种服装最多购进75件;
(2)设总利润为w元,因为甲种服装不少于65件,所以65≤x≤75.
则w=(40-a)x+30(100-x)=(10-a)x+3
000.
当0
所以当x=75时,w有最大值,则购进甲种服装75件,乙种服装25件;
当a=10时,所有方案获利相同,所以按哪种方案进货都可以(甲种服装进货量在65~75件之间);
当10
6.(2016丽水中考)2016年3月27日“丽水半程马拉松竞赛”在莲都举行,某运动员从起点万地广场西门出发,途径紫金大桥,沿比赛路线跑回终点万地广场西门.设该运动员离开起点的路程s(km)与跑步时间t(min)之间的函数关系如图所示.其中从起点到紫金大桥的平均速度是0.3
km/min.用时35
min,根据图象提供的信息,解答下列问题:
(1)求图中a的值;
(2)组委会在距离起点2.1
km处设立一个拍摄点C,该运动员从第一次过点C到第二次过点C所用的时间为68
min.
①求AB所在直线的函数解析式;
②该运动员跑完赛程用时多少分钟?
解:(1)∵从起点到紫金大桥的平均速度是0.3
km/min,用时35
min.
∴a=0.3×35=10.5(km);
(2)①∵线段OA经过点O(0,0),A(35,10.5),∴OA的函数解析式是s=0.3t(0≤t≤35).
∴当s=2.1时,0.3t=2.1,解得t=7.
∴该运动员从第一次过C点到第二次过C点所用的时间为68
min.
∴该运动员从起点到第二次过C点共用的时间是7+68=75(min).
∴AB经过(35,10.5),(75,2.1)两点.
设AB所在直线的函数解析式是s=kt+b.
∴解得
∴AB所在直线的函数解析式是s=-0.21t+17.85;
②∵该运动员跑完赛程所用的时间即为直线AB与x轴交点横坐标的值.
∴当s=0时,-0.21t+17.85=0,解得t=85.
∴该运动员跑完赛程用时85
min.
7.(2016包头中考)我市某养殖场计划购买甲、乙两种鱼苗共700尾,甲种鱼苗每尾3元,乙种鱼苗每尾5元,相关资料表明:甲、乙两种鱼苗的成活率分别为85%和90%.
(1)若购买这两种鱼苗共用去2
500元,则甲、乙两种鱼苗各购买多少尾?
(2)若要使这批鱼苗的总成活率不低于88%,则甲种鱼苗至多购买多少尾?
(3)在(2)的条件下,应如何选购鱼苗,使购买鱼苗的费用最低?并求出最低费用.
解:(1)设购买甲种鱼苗x尾,乙种鱼苗y尾,根据题意可得:解得
答:购买甲种鱼苗500尾,乙种鱼苗200尾;
(2)设购买甲种鱼苗z尾,乙种鱼苗(700-z)尾,列不等式得:85%z+90%(700-z)≥700×88%,解得z≤280.
答:甲种鱼苗至多购买280尾;
(3)设甲种鱼苗购买m尾,购买鱼苗的费用为w元,则w=3m+5(700-m)=-2m+3
500,
∵-2<0,∴w随m的增大而减小.
∵0
940(元).
∴700-m=420.
答:当选购甲种鱼苗280尾,乙种鱼苗420尾时,总费用最低,最低费用为2
940元.
同课章节目录
