2017河北中考数学2.1一次方程与方程组及应用教材知识梳理
文档属性
| 名称 | 2017河北中考数学2.1一次方程与方程组及应用教材知识梳理 |
|
|
| 格式 | zip | ||
| 文件大小 | 173.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-01-01 00:00:00 | ||
图片预览




文档简介
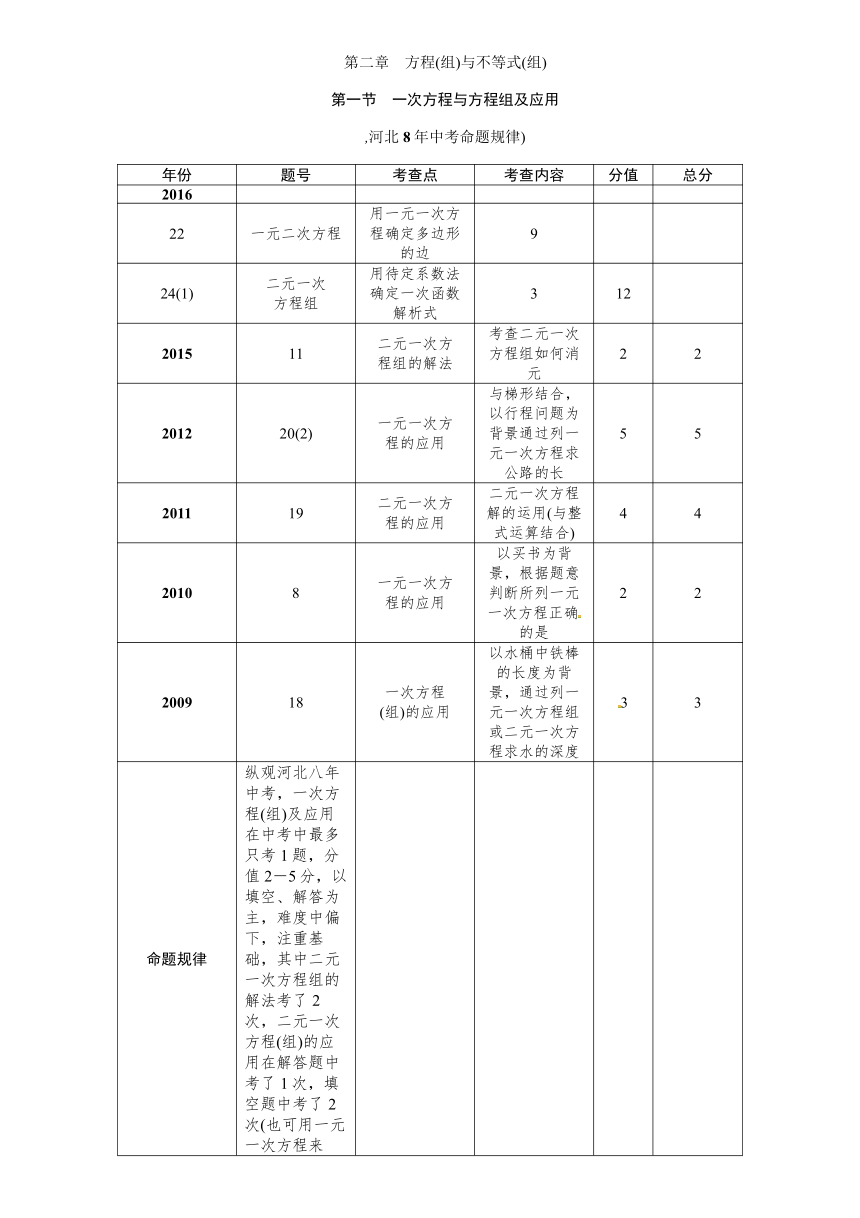
第二章 方程(组)与不等式(组)
第一节 一次方程与方程组及应用
,河北8年中考命题规律)
年份
题号
考查点
考查内容
分值
总分
2016
22
一元二次方程
用一元一次方程确定多边形的边
9
24(1)
二元一次方程组
用待定系数法确定一次函数解析式
3
12
2015
11
二元一次方程组的解法
考查二元一次方程组如何消元
2
2
2012
20(2)
一元一次方程的应用
与梯形结合,以行程问题为背景通过列一元一次方程求公路的长
5
5
2011
19
二元一次方程的应用
二元一次方程解的运用(与整式运算结合)
4
4
2010
8
一元一次方程的应用
以买书为背景,根据题意判断所列一元一次方程正确的是
2
2
2009
18
一次方程(组)的应用
以水桶中铁棒的长度为背景,通过列一元一次方程组或二元一次方程求水的深度
3
3
命题规律
纵观河北八年中考,一次方程(组)及应用在中考中最多只考1题,分值2-5分,以填空、解答为主,难度中偏下,注重基础,其中二元一次方程组的解法考了2次,二元一次方程(组)的应用在解答题中考了1次,填空题中考了2次(也可用一元一次方程来解),一元一次方程在解答、选择题中各考了1次.2016年还专门考查了一元一次方程解决实际问题中整数解的问题.
命题预测
预计2017年,本考点仍为重点考查内容,难度中下等,故平时应分类强化训练.
,河北8年中考真题及模拟)
INCLUDEPICTURE"命点.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/命点.TIF"
\
MERGEFORMAT
一次方程(组)的应用(7次)
1.(2015河北11题2分)利用加减消元法解方程组,下列做法正确的是( D )
A.要消去y,可以将①×5+②×2
B.要消去x,可以将①×3+②×(-5)
C.要消去y,可以将①×5+②×3
D.要消去x,可以将①×(-5)+②×2
2.(2010河北8题2分)小悦买书需用48元钱,付款时恰好用了1元和5元的纸币共12张,设所用的1元纸币为x张,根据题意,下面所列方程正确的是( A )
A.x+5(12-x)=48
B.x+5(x-12)=48
C.x+12(x-5)=48
D.5x+(12-x)=48
3.(2009河北18题3分)如图,两根铁棒直立于桶底水平的木桶中,在桶中加入水后,一根露出水面的长度是它的,另一根露出水面的长度是它的,两根铁棒长度之和为55
cm,此时木桶中水的深度是__20__cm.
4.(2016河北22题9分)已知n边形的内角和θ=(n-2)×180°.
(1)甲同学说,θ能取360°;而乙同学说,θ也能取630°.甲、乙的说法对吗?若对,求出边数n.若不对,说明理由;
(2)若n边形变为(n+x)边形,发现内角和增加了360°,用列方程的方法确定x.
解:(1)甲对,乙不对.
∵θ=360°,∴(n-2)×180=360.解得n=4.
∵θ=630°,∴(n-2)×180=630,解得n=.
∵n为整数,∴θ不能取630°;
(2)依题意,得(n-2)×180+360=(n+x-2)×180.解得x=2.
5.[2012河北20(2)题5分]如图,某市A,B两地之间有两条公路,一条是市区公路AB,另一条是外环公路AD-DC-CB.这两条公路围成等腰梯形ABCD,其中DC∥AB,AB∶AD∶DC=10∶5∶2.
(1)求外环公路总长和市区公路长的比;
(2)某人驾车从A地出发,沿市区公路去B地,平均速度是40
km/h.返回时沿外环公路行驶,平均速度是80
km/h,结果比去时少用了
h.求市区公路的长.
解:(1)设AB=10x
km,则AD=5x
km,CD=2x
km.∵四边形ABCD是等腰梯形,∴BC=AD=5x
km.∴AD+CD+CB=12x(km).∴外环公路的总长和市区公路长的比为12x∶10x=6∶5;(2)由(1)可知,市区公路的长为10x
km,外环公路的总长为12x
km,由题意得=+,解得x=1,∴10x=10.
答:市区公路的长为10
km.
6.(2016石家庄新华区模拟)若是关于x、y的二元一次方程ax-3y=1的解,则a的值为( A )
A.7
B.2
C.-1
D.-5
7.(2016唐山路南区三模)小明在解关于x、y的二元一次方程组时,解得则△和 代表的数分别是( B )
A.△=1, =5
B.△=5, =1
C.△=-1, =3
D.△=3, =-1
8.(2016石家庄二模)希望中学九年级1班共有学生49人,当该班少一名男生时,男生的人数恰好为女生人数的一半.设该班有男生x人,则下列方程中,正确的是( A )
A.2(x-1)+x=49
B.2(x+1)+x=49
C.x-1+2x=49
D.x+1+2x=49
9.(2016原创)已知关于x,y的二元一次方程ax+by=10(ab≠0)的两个解分别为和求1-a2+4b2的值.
解:将x=-1,y=2代入方程ax+by=10中得:-a+2b=10,将x=-2,y=-4同样代入方程得:-a-2b=5,∴(-a+2b)(-a-2b)=50,∴-a2+4b2=-50,∴1-a2+4b2=1-50=-49.
,中考考点清单)
INCLUDEPICTURE"考点1.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/考点1.TIF"
\
MERGEFORMAT
方程、方程的解与解方程
1.含有未知数的__等式__叫方程.
2.使方程左右两边相等的__未知数__的值叫方程的解.
3.求方程__解__的过程叫解方程.
INCLUDEPICTURE"考点2.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/考点2.TIF"
\
MERGEFORMAT
等式的基本性质
4.
性质1
等式两边同时加上(或减去)同一个数或同一个式子,所得的结果仍①__相等__.如果a=b,那么a±c②__=__b±c.
续表
性质2
等式两边同时乘以(或除以)同一个数(除数不为0),所得结果仍③__相等__.如果a=b,那么ac=bc(c≠0),=(c≠0).
INCLUDEPICTURE"考点3.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/考点3.TIF"
\
MERGEFORMAT
一次方程(组)
5.
概念
解法
一元一次方程
含有①__一个__未知数且未知数的次数是②__1__,这样的方程叫做一元一次方程.
解一元一次方程的一般步骤:(1)去分母;(2)去括号;(3)移项;(4)合并同类项;(5)系数化为1.
续表
二元一次方程
含有两个③__未知数__,并且含有未知数的项的④__次数__都是1的方程叫做二元一次方程.
一般需找出满足方程的整数解即可.
二元一次方程组
两个⑤__二元一次方程__所组成的一组方程,叫做二元一次方程组.
解二元一次方程组的基本思路是⑥__消元__.基本解法有:⑦__代入__消元法和⑧__加减__消元法.
【易错提示】(1)解一元一次方程去分母时常数项不要漏乘,移项一定要变号;(2)二元一次方程组的解应写成的形式.
INCLUDEPICTURE"考点4.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/考点4.TIF"
\
MERGEFORMAT
列方程(组)解应用题的一般步骤
6.
(1)审
审清题意,分清题中的已知量、未知量;
(2)设
设①__未知数__,设其中某个量为未知数,并注意单位,对含有两个未知数的问题,需设两个未知数;
续表
(3)列
弄清题意,找出②__相等关系__;根据③__相等关系__,列方程(组);
(4)解
解方程(组);
(5)验
检验结果是否符合题意;
(6)答
答题(包括单位).
【方法点拨】一次方程(组)用到的思想方法:
(1)消元思想:将二元一次方程组通过消元使其变成一元一次方程.
(2)整体思想:在解方程时结合方程的结构特点,灵活采取整体思想,使整个过程简捷.
(3)转化思想:解一元一次方程最终要转化成ax=b;解二元一次方程组先转化成一元一次方程.
(4)数形结合思想:利用图形的性质建立方程模型解决几何图形中的问题.
(5)方程思想:利用其他知识构造方程解决问题.
,中考重难点突破)
INCLUDEPICTURE"类型1.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/类型1.TIF"
\
MERGEFORMAT
一元一次方程及解法
【例1】(1)(2015娄底中考)已知关于x的方程2x+a-5=0的解是x=2,则a的值为________;
(2)解方程:-x=-.
【学生解答】(1)1;(2)原方程可化为:-x=-,解得x=-5.
【点拨】(1)把x=2代入即可;(2)先“化零为整”,再按去分母→去括号→移项→合并同类项→系数化为1来解.
INCLUDEPICTURE"针对.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/针对.TIF"
\
MERGEFORMAT
1.(2016厦门中考)方程x+5=(x+3)的解是__x=-7__.
2.(2016滨州中考)解方程2-=.
解:去分母得:12-2(2x+1)=3(1+x),去括号得:12-4x-2=3+3x,解得x=1.
INCLUDEPICTURE"类型2.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/类型2.TIF"
\
MERGEFORMAT
二元一次方程组及解法
【例2】(2016无锡中考)解方程组:
【学生解答】由②得2x-2y=1③.
①-③,得y=4.
把y=4代入①,得x=.
∴原方程组的解为
【点拨】解二元一次方程组的两种方法(代入法和加减法)用到的都是“消元”的思想,具体解题时两种方法可根据方程组中未知数系数的特点灵活运用.
INCLUDEPICTURE"针对.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/针对.TIF"
\
MERGEFORMAT
3.(2016杭州中考)设实数x,y满足方程组则x+y=__8__.
4.解方程组:
解:由①,得x-2y=-2.
由②,得3x-4y=2.
①×2-②,得x=6.把x=6代入①得y=4,
所以原方程组的解为
INCLUDEPICTURE"类型3.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/类型3.TIF"
\
MERGEFORMAT
一次方程(组)的应用
【例3】某公园的门票价格如下表:
购票人数
1~50
51~100
100以上
票价(元/人)
10
8
5
某校九年级甲、乙两个班共有100多人去该公园举行毕业联欢活动,其中甲班有50多人,乙班不足50人.如果以班为单位分别买门票,两个班一共应付920元;如果两个班联合起来作为一个团体购票,一共只要515元.问:甲、乙两班分别有多少人?
【解析】由两班单独购票时甲班票价8元/人,乙班票价10元/人,两个班共付920元及购团体票时票价5元/人,共付款515元,可列方程组求解.
【学生解答】设甲、乙两班分别有x人和y人,得
解得
答:甲班55人,乙班48人.
【方法归纳】综合表格中的信息与文字叙述,理解题意是解决本题的关键.
INCLUDEPICTURE"针对.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/针对.TIF"
\
MERGEFORMAT
5.(2016江西中考)小锦和小丽购买了价格分别相同的中性笔和笔芯.小锦买了20支笔和2盒笔芯,用了56元;小丽买了2支笔和3盒笔芯,仅用了28元.求每支中性笔和每盒笔芯的价格.
解:设每支中性笔x元,每盒笔芯y元,根据题意得
解得
答:每支中性笔2元,每盒笔芯8元.
6.(2016资阳改编)学校需要购买一批篮球和足球,已知一个篮球比一个足球的进价高30元,买两个篮球和三个足球一共需要510元.求篮球和足球的单价.
解:设一个篮球x元,则一个足球(x-30)元,由题意得2x+3(x-30)=510.解得x=120.
答:一个篮球120元,一个足球90元.
,中考备考方略)
INCLUDEPICTURE"基础训练.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/基础训练.TIF"
\
MERGEFORMAT
1.(2015重庆中考)已知关于x的方程2x+m-8=0的解是x=3,则m的值为( A )
A.2
B.3
C.4
D.5
2.(2016邯郸十一中模拟)若2a=3b,则下列各式中不成立的是( D )
A.4a=6b
B.2a+5=3b+5
C.=
D.a=3b
3.(2016株洲中考)在解方程+x=时,方程两边同时乘以6,去分母后,正确的是( B )
A.2x-1+6x=3(3x+1)
B.2(x-1)+6x=3(3x+1)
C.2(x-1)+x=3(3x+1)
D.(x-1)+x=3(x+1)
4.(2016广州中考)已知a,b满足方程组则a+b的值为( B )
A.-4
B.4
C.-2
D.2
5.(2016廊坊二模)已知是二元一次方程组的解,则m-n的值是( D )
A.1
B.2
C.3
D.4
6.(2016杭州中考)已知甲煤场有煤518吨,乙煤场有煤106吨,为了使甲煤场存煤是乙煤场的2倍,需要从甲煤场运煤到乙煤场,设从甲煤场运煤x吨到乙煤场,则可列方程为( C )
A.518=2(106+x)
B.518-x=2×106
C.518-x=2(106+x)
D.518+x=2(106-x)
7.(2016聊城中考)在如图的2016年6月份的月历表中,任意框出表中竖列上三个相邻的数,这三个数的和不可能是( D )
日
一
二
三
四
五
六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
A.27
B.51
C.69
D.72
8.(2016台湾中考)若二元一次联立方程式的解为x=a,y=b,则a+b的值为( D )
A.
B.
C.7
D.13
9.(2016温州中考)已知甲、乙两数的和是7,甲数是乙数的2倍.设甲数为x,乙数为y,根据题意,列方程组正确的是( A )
A.
B.
C.
D.
10.(2016临沂中考)为了绿化校园,30名学生共种78棵树苗.其中男生每人种3棵,女生每人种2棵,该班男生有x人,女生有y人.根据题意,所列方程组正确的是( D )
A.
B.
C.
D.
11.(2016深圳中考)某商品的标价为200元,8折销售仍赚40元,则商品进价为________元( B )
A.140
B.120
C.160
D.100
12.(1)(2016永州中考)方程组的解是____ ,;)
(2)(2016温州中考)方程组的解是____ ,.)
13.(2016扬州中考)以方程组的解为坐标的点(x,y)在第__二__象限.
14.(2016原创)已知是方程组的解,则代数式(a+b)(a-b)的值为__-8__.
15.(2016石家庄四十二中一模改编)若关于x,y的二元一次方程组的解也是二元一次方程2x+3y=6的解,求k的值.
解:解方程组得
代入2x+3y=6中得k=.
16.(2016福州中考)某班去看演出,甲种票每张24元,乙种票每张18元.如果35名学生购票恰好用去750元,那么甲、乙两种票各买了多少张?
解:设甲种票买了x张,则乙种票买了(35-x)张,由题意得24x+18(35-x)=750,解得x=20,∴35-x=15.
答:甲种票买了20张,乙种票买了15张.
INCLUDEPICTURE"能力提升.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/能力提升.TIF"
\
MERGEFORMAT
17.(2016原创)按如图的运算程序,能使输出结果为3的x,y的值是( D )
A.x=5,y=-2
B.x=3,y=-3
C.x=-4,y=2
D.x=-3,y=-9
18.(2016原创)小亮解二元一次方程组
的解为由于不小心滴上了两滴墨水,刚好遮住了两个数●和★,则●+★=__6__.
19.(2016盐城中考)李师傅加工1个甲种零件和1个乙种零件的时间分别是固定的,现知道李师傅加工3个甲种零件和5个乙种零件共需55
min;加工4个甲种零件和9个乙种零件共需85
min,则李师傅加工2个甲种零件和4个乙种零件共需__40__min.
20.(2016石家庄41中一模)定义一种新运算“ ”:a b=a-2b,比如:2 (-3)=2-2×(-3)=2+6=8.
(1)求(-3) 2的值;
(2)若(x-3) (x+1)=1,求x的值.
解:(1)(-3) 2=(-3)-2×2=-3-4=-7;
(2)∵(x-3) (x+1)=1,∴(x-3)-2(x+1)=1.∴x=-6.
21.(2016石家庄四十一中模拟)用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成,硬纸板以如图两种方法裁剪(裁剪后边角不再利用).
A方法:剪6个侧面;
B方法:剪4个侧面和5个底面.
现有19张硬纸板,裁剪时x张用A方法,其余用B方法.
(1)用x的代数式分别表示裁剪出的侧面和底面个数;
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
解:(1)裁剪出的侧面个数为6x+4(19-x)=(2x+76)个,裁剪出的底面个数为5(19-x)=(-5x+95)个;
(2)由题意得=,解得x=7.
当x=7时,=30.
答:能做30个盒子.
22.(2016沧州八中模拟)P表示n边形的对角线的交点个数(指落在其内部的交点),如果这些交点都不重合,那么P与n的关系式是:P=·(n2-an+b)(其中a,b是常数,n≥4).
(1)填空:通过画图可得:
四边形时,P=__1__(填数字),五边形时,P=__5__(填数字);
(2)请根据四边形和五边形对角线交点的个数,结合关系式,求a,b的值.(注:本题的多边形均指凸多边形)
解:将上述值代入公式可得
化简得
解得
23.(2016连云港中考)某数学兴趣小组研究我国古代《算法统宗》里这样一首诗:我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.诗中后两句的意思是:如果每一间客房住7人,那么有7人无房可住;如果每一间客房住9人,那么就空出一间房.
(1)求该店有客房多少间?房客多少人?
(2)假设店主李三公将客房进行改造后,房间数大大增加.每间客房收费20钱,且每间客房最多入住4人,一次性订客房18间以上(含18间),房费按8折优惠.若诗中“众客”再次一起入住,他们如何订房更合算?
解:(1)设该店有客房x间,有房客y人,
根据题意得:
解得
答:该店有客房8间,房客63人;
(2)若每间客房住4人,则63名客人至少需客房16间,需付费20×16=320钱;若一次性订客房18间,则需付费20×18×0.8=288钱<320钱;
答:诗中“众客”再次一起入住,他们应选择一次性订房18间更合算.
第一节 一次方程与方程组及应用
,河北8年中考命题规律)
年份
题号
考查点
考查内容
分值
总分
2016
22
一元二次方程
用一元一次方程确定多边形的边
9
24(1)
二元一次方程组
用待定系数法确定一次函数解析式
3
12
2015
11
二元一次方程组的解法
考查二元一次方程组如何消元
2
2
2012
20(2)
一元一次方程的应用
与梯形结合,以行程问题为背景通过列一元一次方程求公路的长
5
5
2011
19
二元一次方程的应用
二元一次方程解的运用(与整式运算结合)
4
4
2010
8
一元一次方程的应用
以买书为背景,根据题意判断所列一元一次方程正确的是
2
2
2009
18
一次方程(组)的应用
以水桶中铁棒的长度为背景,通过列一元一次方程组或二元一次方程求水的深度
3
3
命题规律
纵观河北八年中考,一次方程(组)及应用在中考中最多只考1题,分值2-5分,以填空、解答为主,难度中偏下,注重基础,其中二元一次方程组的解法考了2次,二元一次方程(组)的应用在解答题中考了1次,填空题中考了2次(也可用一元一次方程来解),一元一次方程在解答、选择题中各考了1次.2016年还专门考查了一元一次方程解决实际问题中整数解的问题.
命题预测
预计2017年,本考点仍为重点考查内容,难度中下等,故平时应分类强化训练.
,河北8年中考真题及模拟)
INCLUDEPICTURE"命点.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/命点.TIF"
\
MERGEFORMAT
一次方程(组)的应用(7次)
1.(2015河北11题2分)利用加减消元法解方程组,下列做法正确的是( D )
A.要消去y,可以将①×5+②×2
B.要消去x,可以将①×3+②×(-5)
C.要消去y,可以将①×5+②×3
D.要消去x,可以将①×(-5)+②×2
2.(2010河北8题2分)小悦买书需用48元钱,付款时恰好用了1元和5元的纸币共12张,设所用的1元纸币为x张,根据题意,下面所列方程正确的是( A )
A.x+5(12-x)=48
B.x+5(x-12)=48
C.x+12(x-5)=48
D.5x+(12-x)=48
3.(2009河北18题3分)如图,两根铁棒直立于桶底水平的木桶中,在桶中加入水后,一根露出水面的长度是它的,另一根露出水面的长度是它的,两根铁棒长度之和为55
cm,此时木桶中水的深度是__20__cm.
4.(2016河北22题9分)已知n边形的内角和θ=(n-2)×180°.
(1)甲同学说,θ能取360°;而乙同学说,θ也能取630°.甲、乙的说法对吗?若对,求出边数n.若不对,说明理由;
(2)若n边形变为(n+x)边形,发现内角和增加了360°,用列方程的方法确定x.
解:(1)甲对,乙不对.
∵θ=360°,∴(n-2)×180=360.解得n=4.
∵θ=630°,∴(n-2)×180=630,解得n=.
∵n为整数,∴θ不能取630°;
(2)依题意,得(n-2)×180+360=(n+x-2)×180.解得x=2.
5.[2012河北20(2)题5分]如图,某市A,B两地之间有两条公路,一条是市区公路AB,另一条是外环公路AD-DC-CB.这两条公路围成等腰梯形ABCD,其中DC∥AB,AB∶AD∶DC=10∶5∶2.
(1)求外环公路总长和市区公路长的比;
(2)某人驾车从A地出发,沿市区公路去B地,平均速度是40
km/h.返回时沿外环公路行驶,平均速度是80
km/h,结果比去时少用了
h.求市区公路的长.
解:(1)设AB=10x
km,则AD=5x
km,CD=2x
km.∵四边形ABCD是等腰梯形,∴BC=AD=5x
km.∴AD+CD+CB=12x(km).∴外环公路的总长和市区公路长的比为12x∶10x=6∶5;(2)由(1)可知,市区公路的长为10x
km,外环公路的总长为12x
km,由题意得=+,解得x=1,∴10x=10.
答:市区公路的长为10
km.
6.(2016石家庄新华区模拟)若是关于x、y的二元一次方程ax-3y=1的解,则a的值为( A )
A.7
B.2
C.-1
D.-5
7.(2016唐山路南区三模)小明在解关于x、y的二元一次方程组时,解得则△和 代表的数分别是( B )
A.△=1, =5
B.△=5, =1
C.△=-1, =3
D.△=3, =-1
8.(2016石家庄二模)希望中学九年级1班共有学生49人,当该班少一名男生时,男生的人数恰好为女生人数的一半.设该班有男生x人,则下列方程中,正确的是( A )
A.2(x-1)+x=49
B.2(x+1)+x=49
C.x-1+2x=49
D.x+1+2x=49
9.(2016原创)已知关于x,y的二元一次方程ax+by=10(ab≠0)的两个解分别为和求1-a2+4b2的值.
解:将x=-1,y=2代入方程ax+by=10中得:-a+2b=10,将x=-2,y=-4同样代入方程得:-a-2b=5,∴(-a+2b)(-a-2b)=50,∴-a2+4b2=-50,∴1-a2+4b2=1-50=-49.
,中考考点清单)
INCLUDEPICTURE"考点1.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/考点1.TIF"
\
MERGEFORMAT
方程、方程的解与解方程
1.含有未知数的__等式__叫方程.
2.使方程左右两边相等的__未知数__的值叫方程的解.
3.求方程__解__的过程叫解方程.
INCLUDEPICTURE"考点2.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/考点2.TIF"
\
MERGEFORMAT
等式的基本性质
4.
性质1
等式两边同时加上(或减去)同一个数或同一个式子,所得的结果仍①__相等__.如果a=b,那么a±c②__=__b±c.
续表
性质2
等式两边同时乘以(或除以)同一个数(除数不为0),所得结果仍③__相等__.如果a=b,那么ac=bc(c≠0),=(c≠0).
INCLUDEPICTURE"考点3.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/考点3.TIF"
\
MERGEFORMAT
一次方程(组)
5.
概念
解法
一元一次方程
含有①__一个__未知数且未知数的次数是②__1__,这样的方程叫做一元一次方程.
解一元一次方程的一般步骤:(1)去分母;(2)去括号;(3)移项;(4)合并同类项;(5)系数化为1.
续表
二元一次方程
含有两个③__未知数__,并且含有未知数的项的④__次数__都是1的方程叫做二元一次方程.
一般需找出满足方程的整数解即可.
二元一次方程组
两个⑤__二元一次方程__所组成的一组方程,叫做二元一次方程组.
解二元一次方程组的基本思路是⑥__消元__.基本解法有:⑦__代入__消元法和⑧__加减__消元法.
【易错提示】(1)解一元一次方程去分母时常数项不要漏乘,移项一定要变号;(2)二元一次方程组的解应写成的形式.
INCLUDEPICTURE"考点4.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/考点4.TIF"
\
MERGEFORMAT
列方程(组)解应用题的一般步骤
6.
(1)审
审清题意,分清题中的已知量、未知量;
(2)设
设①__未知数__,设其中某个量为未知数,并注意单位,对含有两个未知数的问题,需设两个未知数;
续表
(3)列
弄清题意,找出②__相等关系__;根据③__相等关系__,列方程(组);
(4)解
解方程(组);
(5)验
检验结果是否符合题意;
(6)答
答题(包括单位).
【方法点拨】一次方程(组)用到的思想方法:
(1)消元思想:将二元一次方程组通过消元使其变成一元一次方程.
(2)整体思想:在解方程时结合方程的结构特点,灵活采取整体思想,使整个过程简捷.
(3)转化思想:解一元一次方程最终要转化成ax=b;解二元一次方程组先转化成一元一次方程.
(4)数形结合思想:利用图形的性质建立方程模型解决几何图形中的问题.
(5)方程思想:利用其他知识构造方程解决问题.
,中考重难点突破)
INCLUDEPICTURE"类型1.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/类型1.TIF"
\
MERGEFORMAT
一元一次方程及解法
【例1】(1)(2015娄底中考)已知关于x的方程2x+a-5=0的解是x=2,则a的值为________;
(2)解方程:-x=-.
【学生解答】(1)1;(2)原方程可化为:-x=-,解得x=-5.
【点拨】(1)把x=2代入即可;(2)先“化零为整”,再按去分母→去括号→移项→合并同类项→系数化为1来解.
INCLUDEPICTURE"针对.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/针对.TIF"
\
MERGEFORMAT
1.(2016厦门中考)方程x+5=(x+3)的解是__x=-7__.
2.(2016滨州中考)解方程2-=.
解:去分母得:12-2(2x+1)=3(1+x),去括号得:12-4x-2=3+3x,解得x=1.
INCLUDEPICTURE"类型2.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/类型2.TIF"
\
MERGEFORMAT
二元一次方程组及解法
【例2】(2016无锡中考)解方程组:
【学生解答】由②得2x-2y=1③.
①-③,得y=4.
把y=4代入①,得x=.
∴原方程组的解为
【点拨】解二元一次方程组的两种方法(代入法和加减法)用到的都是“消元”的思想,具体解题时两种方法可根据方程组中未知数系数的特点灵活运用.
INCLUDEPICTURE"针对.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/针对.TIF"
\
MERGEFORMAT
3.(2016杭州中考)设实数x,y满足方程组则x+y=__8__.
4.解方程组:
解:由①,得x-2y=-2.
由②,得3x-4y=2.
①×2-②,得x=6.把x=6代入①得y=4,
所以原方程组的解为
INCLUDEPICTURE"类型3.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/类型3.TIF"
\
MERGEFORMAT
一次方程(组)的应用
【例3】某公园的门票价格如下表:
购票人数
1~50
51~100
100以上
票价(元/人)
10
8
5
某校九年级甲、乙两个班共有100多人去该公园举行毕业联欢活动,其中甲班有50多人,乙班不足50人.如果以班为单位分别买门票,两个班一共应付920元;如果两个班联合起来作为一个团体购票,一共只要515元.问:甲、乙两班分别有多少人?
【解析】由两班单独购票时甲班票价8元/人,乙班票价10元/人,两个班共付920元及购团体票时票价5元/人,共付款515元,可列方程组求解.
【学生解答】设甲、乙两班分别有x人和y人,得
解得
答:甲班55人,乙班48人.
【方法归纳】综合表格中的信息与文字叙述,理解题意是解决本题的关键.
INCLUDEPICTURE"针对.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/针对.TIF"
\
MERGEFORMAT
5.(2016江西中考)小锦和小丽购买了价格分别相同的中性笔和笔芯.小锦买了20支笔和2盒笔芯,用了56元;小丽买了2支笔和3盒笔芯,仅用了28元.求每支中性笔和每盒笔芯的价格.
解:设每支中性笔x元,每盒笔芯y元,根据题意得
解得
答:每支中性笔2元,每盒笔芯8元.
6.(2016资阳改编)学校需要购买一批篮球和足球,已知一个篮球比一个足球的进价高30元,买两个篮球和三个足球一共需要510元.求篮球和足球的单价.
解:设一个篮球x元,则一个足球(x-30)元,由题意得2x+3(x-30)=510.解得x=120.
答:一个篮球120元,一个足球90元.
,中考备考方略)
INCLUDEPICTURE"基础训练.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/基础训练.TIF"
\
MERGEFORMAT
1.(2015重庆中考)已知关于x的方程2x+m-8=0的解是x=3,则m的值为( A )
A.2
B.3
C.4
D.5
2.(2016邯郸十一中模拟)若2a=3b,则下列各式中不成立的是( D )
A.4a=6b
B.2a+5=3b+5
C.=
D.a=3b
3.(2016株洲中考)在解方程+x=时,方程两边同时乘以6,去分母后,正确的是( B )
A.2x-1+6x=3(3x+1)
B.2(x-1)+6x=3(3x+1)
C.2(x-1)+x=3(3x+1)
D.(x-1)+x=3(x+1)
4.(2016广州中考)已知a,b满足方程组则a+b的值为( B )
A.-4
B.4
C.-2
D.2
5.(2016廊坊二模)已知是二元一次方程组的解,则m-n的值是( D )
A.1
B.2
C.3
D.4
6.(2016杭州中考)已知甲煤场有煤518吨,乙煤场有煤106吨,为了使甲煤场存煤是乙煤场的2倍,需要从甲煤场运煤到乙煤场,设从甲煤场运煤x吨到乙煤场,则可列方程为( C )
A.518=2(106+x)
B.518-x=2×106
C.518-x=2(106+x)
D.518+x=2(106-x)
7.(2016聊城中考)在如图的2016年6月份的月历表中,任意框出表中竖列上三个相邻的数,这三个数的和不可能是( D )
日
一
二
三
四
五
六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
A.27
B.51
C.69
D.72
8.(2016台湾中考)若二元一次联立方程式的解为x=a,y=b,则a+b的值为( D )
A.
B.
C.7
D.13
9.(2016温州中考)已知甲、乙两数的和是7,甲数是乙数的2倍.设甲数为x,乙数为y,根据题意,列方程组正确的是( A )
A.
B.
C.
D.
10.(2016临沂中考)为了绿化校园,30名学生共种78棵树苗.其中男生每人种3棵,女生每人种2棵,该班男生有x人,女生有y人.根据题意,所列方程组正确的是( D )
A.
B.
C.
D.
11.(2016深圳中考)某商品的标价为200元,8折销售仍赚40元,则商品进价为________元( B )
A.140
B.120
C.160
D.100
12.(1)(2016永州中考)方程组的解是____ ,;)
(2)(2016温州中考)方程组的解是____ ,.)
13.(2016扬州中考)以方程组的解为坐标的点(x,y)在第__二__象限.
14.(2016原创)已知是方程组的解,则代数式(a+b)(a-b)的值为__-8__.
15.(2016石家庄四十二中一模改编)若关于x,y的二元一次方程组的解也是二元一次方程2x+3y=6的解,求k的值.
解:解方程组得
代入2x+3y=6中得k=.
16.(2016福州中考)某班去看演出,甲种票每张24元,乙种票每张18元.如果35名学生购票恰好用去750元,那么甲、乙两种票各买了多少张?
解:设甲种票买了x张,则乙种票买了(35-x)张,由题意得24x+18(35-x)=750,解得x=20,∴35-x=15.
答:甲种票买了20张,乙种票买了15张.
INCLUDEPICTURE"能力提升.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/能力提升.TIF"
\
MERGEFORMAT
17.(2016原创)按如图的运算程序,能使输出结果为3的x,y的值是( D )
A.x=5,y=-2
B.x=3,y=-3
C.x=-4,y=2
D.x=-3,y=-9
18.(2016原创)小亮解二元一次方程组
的解为由于不小心滴上了两滴墨水,刚好遮住了两个数●和★,则●+★=__6__.
19.(2016盐城中考)李师傅加工1个甲种零件和1个乙种零件的时间分别是固定的,现知道李师傅加工3个甲种零件和5个乙种零件共需55
min;加工4个甲种零件和9个乙种零件共需85
min,则李师傅加工2个甲种零件和4个乙种零件共需__40__min.
20.(2016石家庄41中一模)定义一种新运算“ ”:a b=a-2b,比如:2 (-3)=2-2×(-3)=2+6=8.
(1)求(-3) 2的值;
(2)若(x-3) (x+1)=1,求x的值.
解:(1)(-3) 2=(-3)-2×2=-3-4=-7;
(2)∵(x-3) (x+1)=1,∴(x-3)-2(x+1)=1.∴x=-6.
21.(2016石家庄四十一中模拟)用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成,硬纸板以如图两种方法裁剪(裁剪后边角不再利用).
A方法:剪6个侧面;
B方法:剪4个侧面和5个底面.
现有19张硬纸板,裁剪时x张用A方法,其余用B方法.
(1)用x的代数式分别表示裁剪出的侧面和底面个数;
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
解:(1)裁剪出的侧面个数为6x+4(19-x)=(2x+76)个,裁剪出的底面个数为5(19-x)=(-5x+95)个;
(2)由题意得=,解得x=7.
当x=7时,=30.
答:能做30个盒子.
22.(2016沧州八中模拟)P表示n边形的对角线的交点个数(指落在其内部的交点),如果这些交点都不重合,那么P与n的关系式是:P=·(n2-an+b)(其中a,b是常数,n≥4).
(1)填空:通过画图可得:
四边形时,P=__1__(填数字),五边形时,P=__5__(填数字);
(2)请根据四边形和五边形对角线交点的个数,结合关系式,求a,b的值.(注:本题的多边形均指凸多边形)
解:将上述值代入公式可得
化简得
解得
23.(2016连云港中考)某数学兴趣小组研究我国古代《算法统宗》里这样一首诗:我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.诗中后两句的意思是:如果每一间客房住7人,那么有7人无房可住;如果每一间客房住9人,那么就空出一间房.
(1)求该店有客房多少间?房客多少人?
(2)假设店主李三公将客房进行改造后,房间数大大增加.每间客房收费20钱,且每间客房最多入住4人,一次性订客房18间以上(含18间),房费按8折优惠.若诗中“众客”再次一起入住,他们如何订房更合算?
解:(1)设该店有客房x间,有房客y人,
根据题意得:
解得
答:该店有客房8间,房客63人;
(2)若每间客房住4人,则63名客人至少需客房16间,需付费20×16=320钱;若一次性订客房18间,则需付费20×18×0.8=288钱<320钱;
答:诗中“众客”再次一起入住,他们应选择一次性订房18间更合算.
同课章节目录
