23.2.1解直角三角形及其应用(1)课件(共12张)
文档属性
| 名称 | 23.2.1解直角三角形及其应用(1)课件(共12张) |

|
|
| 格式 | zip | ||
| 文件大小 | 513.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-01-03 09:58:35 | ||
图片预览



文档简介
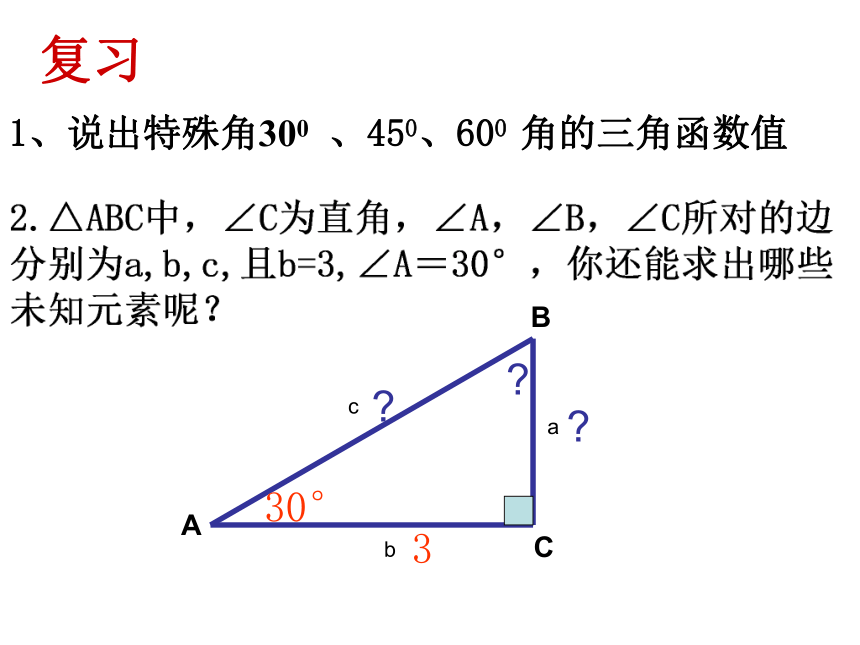
课件12张PPT。23.2 解直角三角形(1)ABCabc330°???1、说出特殊角300 、450、600 角的三角函数值ABCabc330°???复习学习目标:
1、了解解直角三角形的概念
2、能运用直角三角形的角与角(两锐角互余),边与边(勾股定理),边与角之间的关系解直角三角形自学提纲:
阅读书本上第124~125页内容,解决以下问题
1、如图,在Rt△ABC中,共有六个元素(三个边,三个角),其中C=900,填空:
(1)三边之间的关系:a2 +b2 =( )
(2)锐角之间的关系:∠A+∠B=( )
(3)边角之间的关系:sinA=( ),cosA=( ),tanA=( )
2、什么叫解直角三角形?
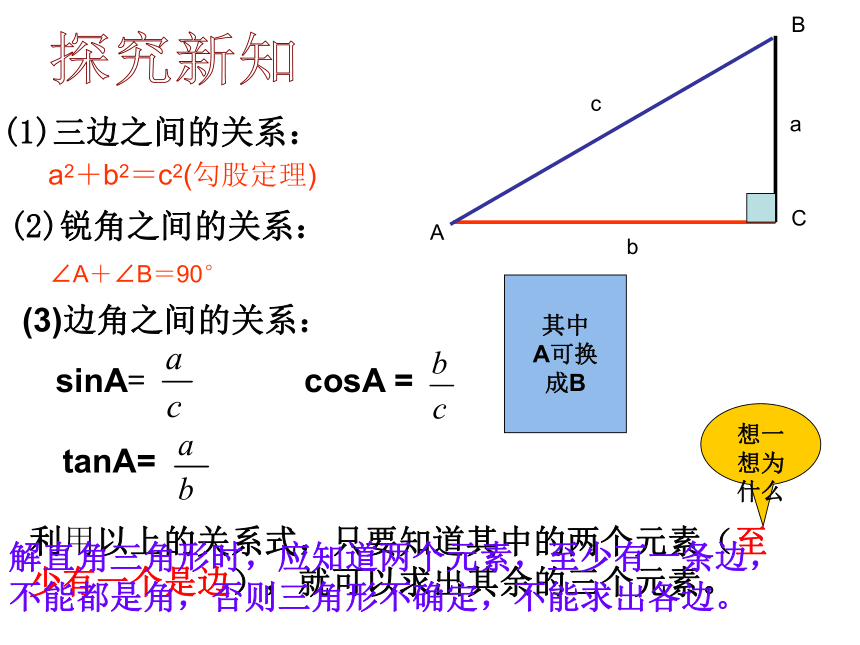
3,看懂书本上例1和例2BCabcA??? (1)三边之间的关系:
???????BCabcA(2)锐角之间的关系: ? a2+b2=c2(勾股定理) ∠A+∠B=90° (3)边角之间的关系: sinA=cosA =tanA=其中
A可换
成B利用以上的关系式,只要知道其中的两个元素(至少有一个是边),就可以求出其余的三个元素。想一想为什么解直角三角形时,应知道两个元素,至少有一条边,
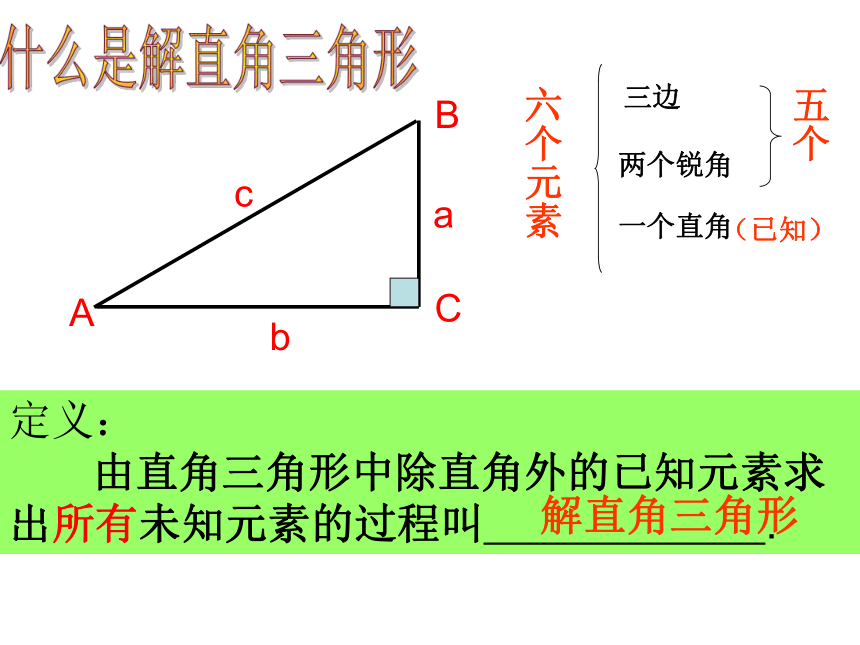
不能都是角,否则三角形不确定,不能求出各边。探究新知六个元素三边两个锐角一个直角(已知)五个定义:
??? 由直角三角形中除直角外的已知元素求出所有未知元素的过程叫 . 解直角三角形什么是解直角三角形例1:在Rt△ABC中,∠C=900 ,∠B=420 6/ ,
c=287.4,解这个直角三角形(精确到0.1) 由cosB = , 得
a=c ? cosB=287.4X0.7420=213.3 由sinB= , 得
b=c ? sinB=287.4x0.6704=192.7解: ∠A=90O- 42O6/=47O54/例2:在△ABC中,∠ A=550,b=20cm,c=30cm ,求三角形的面积 S△ABC(精确到0.1cm2)cABDbc1. 本题得出一个结论:
S△ABC= bcsinA
: S△ABC = absinC, S△ABC= acsinB
是否成立?思考知识拓展2.由此我们可以得到一个重要结论:
三角形的面积等于两边之长及其夹角正弦值之积的一半,即:
S△ABC = bcsinA = absinC= acsinB
1. 本题得出一个结论:
S△ABC= bcsinA
: S△ABC = absinC, S△ABC= acsinB
是否成立?思考
课本125页,练习1,
2(1)、(2)。清点一下你的收获:
1.什么是解直角三角形?
由直角三角形中除直角外的已知元素求出所有未知元素的过程叫解直角三角形
2.解直角三角形的依据是什么???? (1)三边之间的关系:
???????(2)锐角之间的关系: ? a2+b2=c2(勾股定理) ∠A+∠B=90° (3)边角之间的关系: sinA=cosA =tanA=小结作业如图,在△ABC中,已知AC=6,∠C=75°,
∠B=45°,求△ABC的面积。75°ABC┓D⌒450⌒⌒60°6
必做:课本125页:第2(3)(4)、
3题。
选做: 预习:课本126页例3
1、了解解直角三角形的概念
2、能运用直角三角形的角与角(两锐角互余),边与边(勾股定理),边与角之间的关系解直角三角形自学提纲:
阅读书本上第124~125页内容,解决以下问题
1、如图,在Rt△ABC中,共有六个元素(三个边,三个角),其中C=900,填空:
(1)三边之间的关系:a2 +b2 =( )
(2)锐角之间的关系:∠A+∠B=( )
(3)边角之间的关系:sinA=( ),cosA=( ),tanA=( )
2、什么叫解直角三角形?
3,看懂书本上例1和例2BCabcA??? (1)三边之间的关系:
???????BCabcA(2)锐角之间的关系: ? a2+b2=c2(勾股定理) ∠A+∠B=90° (3)边角之间的关系: sinA=cosA =tanA=其中
A可换
成B利用以上的关系式,只要知道其中的两个元素(至少有一个是边),就可以求出其余的三个元素。想一想为什么解直角三角形时,应知道两个元素,至少有一条边,
不能都是角,否则三角形不确定,不能求出各边。探究新知六个元素三边两个锐角一个直角(已知)五个定义:
??? 由直角三角形中除直角外的已知元素求出所有未知元素的过程叫 . 解直角三角形什么是解直角三角形例1:在Rt△ABC中,∠C=900 ,∠B=420 6/ ,
c=287.4,解这个直角三角形(精确到0.1) 由cosB = , 得
a=c ? cosB=287.4X0.7420=213.3 由sinB= , 得
b=c ? sinB=287.4x0.6704=192.7解: ∠A=90O- 42O6/=47O54/例2:在△ABC中,∠ A=550,b=20cm,c=30cm ,求三角形的面积 S△ABC(精确到0.1cm2)cABDbc1. 本题得出一个结论:
S△ABC= bcsinA
: S△ABC = absinC, S△ABC= acsinB
是否成立?思考知识拓展2.由此我们可以得到一个重要结论:
三角形的面积等于两边之长及其夹角正弦值之积的一半,即:
S△ABC = bcsinA = absinC= acsinB
1. 本题得出一个结论:
S△ABC= bcsinA
: S△ABC = absinC, S△ABC= acsinB
是否成立?思考
课本125页,练习1,
2(1)、(2)。清点一下你的收获:
1.什么是解直角三角形?
由直角三角形中除直角外的已知元素求出所有未知元素的过程叫解直角三角形
2.解直角三角形的依据是什么???? (1)三边之间的关系:
???????(2)锐角之间的关系: ? a2+b2=c2(勾股定理) ∠A+∠B=90° (3)边角之间的关系: sinA=cosA =tanA=小结作业如图,在△ABC中,已知AC=6,∠C=75°,
∠B=45°,求△ABC的面积。75°ABC┓D⌒450⌒⌒60°6
必做:课本125页:第2(3)(4)、
3题。
选做: 预习:课本126页例3
