沪科版九年级数学上23.2解直角三角形的应用(2)--仰角俯角课件(共13张)
文档属性
| 名称 | 沪科版九年级数学上23.2解直角三角形的应用(2)--仰角俯角课件(共13张) |

|
|
| 格式 | zip | ||
| 文件大小 | 155.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-01-03 10:01:44 | ||
图片预览



文档简介
课件13张PPT。23.2解直角三角形的应用(2)在直角三角形中,除直角外,由已知元素
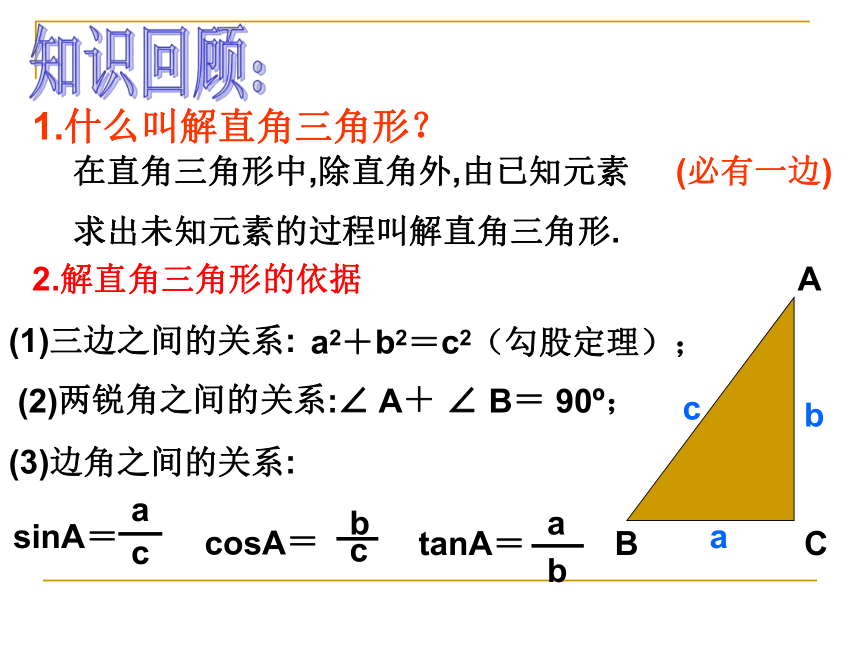
求出未知元素的过程叫解直角三角形.1.什么叫解直角三角形?(1)三边之间的关系:a2+b2=c2(勾股定理);2.解直角三角形的依据(2)两锐角之间的关系:∠ A+ ∠ B= 90o;(3)边角之间的关系:sinA=知识回顾:(必有一边)caBbAC1.了解仰角、俯角的概念,利用解直角三角形的知识解决实际问题。
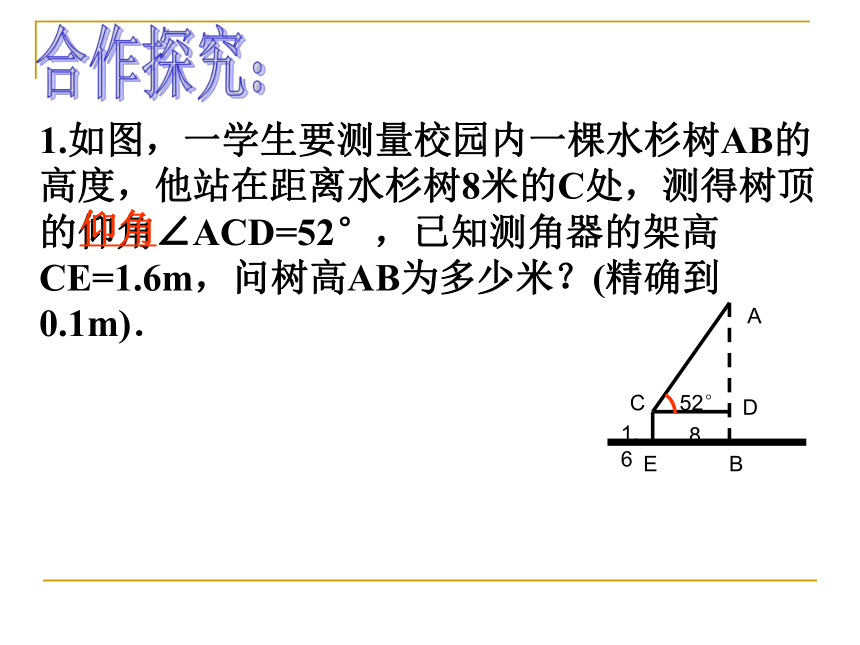
2.将某些实际问题中的数量关系,归结为直角三角形中元素之间的关系,从而解决问题。学习目标:自学提纲:1.如图,一学生要测量校园内一棵水杉树AB的高度,他站在距离水杉树8米的C处,测得树顶的仰角∠ACB=52°,已知测角器的架高CE=1.6m,问树高AB为多少米?(精确到0.1m).3.利用解直角三角形的知识解决实际问题的一般过程是什么?2.仰角和俯角是如何定义的?1.如图,一学生要测量校园内一棵水杉树AB的高度,他站在距离水杉树8米的C处,测得树顶的仰角∠ACD=52°,已知测角器的架高CE=1.6m,问树高AB为多少米?(精确到0.1m).
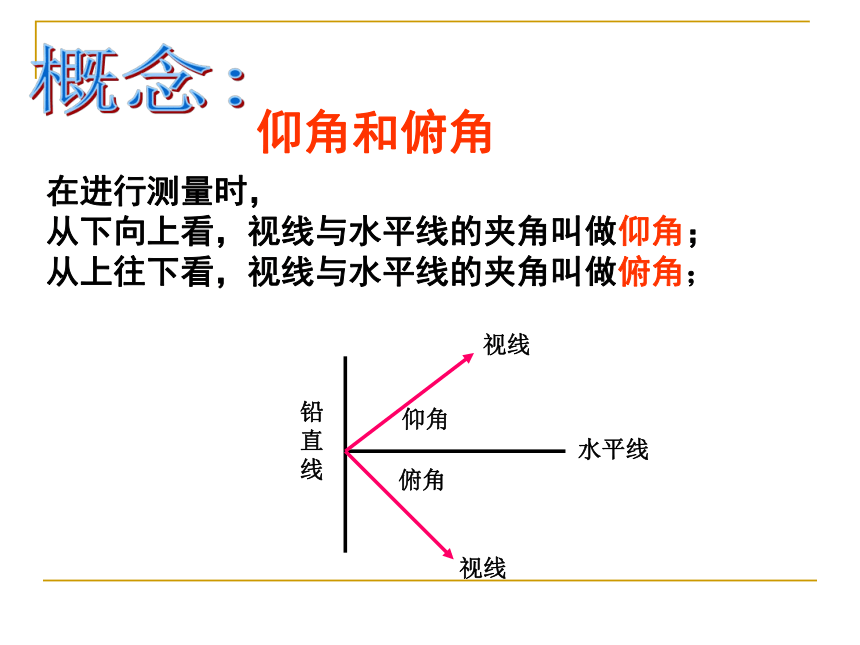
合作探究:仰角仰角和俯角铅直线水平线视线视线仰角俯角在进行测量时,
从下向上看,视线与水平线的夹角叫做仰角;
从上往下看,视线与水平线的夹角叫做俯角;
概念:如图,一学生要测量校园内一棵水杉树的高度,他站在距离水杉树8米的E处,测得树顶的仰角∠ACD=60°,已知测角仪的架高CE= 1.6米,
求树高AB.1.68CABDE变式题1: 如图,一学生要测量校园内一棵水杉树的高度,在C、D两处测得树顶A的仰角分别为30°和45°,若CD=100米,测角器高1米。
求树高AB。30°45°100米变式题2:AEFCBDG1、如图,小芸在自家楼房的窗户A处,测量楼前的一棵树CD的高,现测得树顶C处的俯角为45°,树底D处的俯角为60°,楼底到大树的距离BD为20米,请你帮助小芸计算树的高度。理解应用:2.热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30°,看这栋高楼底部的俯角为60°,热气球与高楼的水平距离为120m,这栋高楼有多高?α=30°β=60°120ABCD1.在解直角三角形应用时经常接触到的一些概念(仰角,俯角;) 小结:2.利用解直角三角形的知识解决实际问题的一般过程是:1).将实际问题抽象为数学问题; (画出平面图形,转化为解直角三角形的问题))2).根据条件的特点,适当选用锐角三角函数等去解直角三角形;3).得到数学问题的答案;4).得到实际问题的答案.课堂作业:
必做题:课本126页 练习1,
选做题:课本126页 练习2
课外作业:同步基训 布置作业: 如图,山顶上有一棵水杉树,在树顶A处测得地面上一点A的俯角α=60°,在树底B处测得C的俯角β=45°,已知树高AB=10米,求山高BD。βα10米DCBA
求出未知元素的过程叫解直角三角形.1.什么叫解直角三角形?(1)三边之间的关系:a2+b2=c2(勾股定理);2.解直角三角形的依据(2)两锐角之间的关系:∠ A+ ∠ B= 90o;(3)边角之间的关系:sinA=知识回顾:(必有一边)caBbAC1.了解仰角、俯角的概念,利用解直角三角形的知识解决实际问题。
2.将某些实际问题中的数量关系,归结为直角三角形中元素之间的关系,从而解决问题。学习目标:自学提纲:1.如图,一学生要测量校园内一棵水杉树AB的高度,他站在距离水杉树8米的C处,测得树顶的仰角∠ACB=52°,已知测角器的架高CE=1.6m,问树高AB为多少米?(精确到0.1m).3.利用解直角三角形的知识解决实际问题的一般过程是什么?2.仰角和俯角是如何定义的?1.如图,一学生要测量校园内一棵水杉树AB的高度,他站在距离水杉树8米的C处,测得树顶的仰角∠ACD=52°,已知测角器的架高CE=1.6m,问树高AB为多少米?(精确到0.1m).
合作探究:仰角仰角和俯角铅直线水平线视线视线仰角俯角在进行测量时,
从下向上看,视线与水平线的夹角叫做仰角;
从上往下看,视线与水平线的夹角叫做俯角;
概念:如图,一学生要测量校园内一棵水杉树的高度,他站在距离水杉树8米的E处,测得树顶的仰角∠ACD=60°,已知测角仪的架高CE= 1.6米,
求树高AB.1.68CABDE变式题1: 如图,一学生要测量校园内一棵水杉树的高度,在C、D两处测得树顶A的仰角分别为30°和45°,若CD=100米,测角器高1米。
求树高AB。30°45°100米变式题2:AEFCBDG1、如图,小芸在自家楼房的窗户A处,测量楼前的一棵树CD的高,现测得树顶C处的俯角为45°,树底D处的俯角为60°,楼底到大树的距离BD为20米,请你帮助小芸计算树的高度。理解应用:2.热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30°,看这栋高楼底部的俯角为60°,热气球与高楼的水平距离为120m,这栋高楼有多高?α=30°β=60°120ABCD1.在解直角三角形应用时经常接触到的一些概念(仰角,俯角;) 小结:2.利用解直角三角形的知识解决实际问题的一般过程是:1).将实际问题抽象为数学问题; (画出平面图形,转化为解直角三角形的问题))2).根据条件的特点,适当选用锐角三角函数等去解直角三角形;3).得到数学问题的答案;4).得到实际问题的答案.课堂作业:
必做题:课本126页 练习1,
选做题:课本126页 练习2
课外作业:同步基训 布置作业: 如图,山顶上有一棵水杉树,在树顶A处测得地面上一点A的俯角α=60°,在树底B处测得C的俯角β=45°,已知树高AB=10米,求山高BD。βα10米DCBA
