23.2解直角三角形的应用(3)--方位角课件(共12张)
文档属性
| 名称 | 23.2解直角三角形的应用(3)--方位角课件(共12张) |  | |
| 格式 | zip | ||
| 文件大小 | 59.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-01-03 10:06:35 | ||
图片预览


文档简介
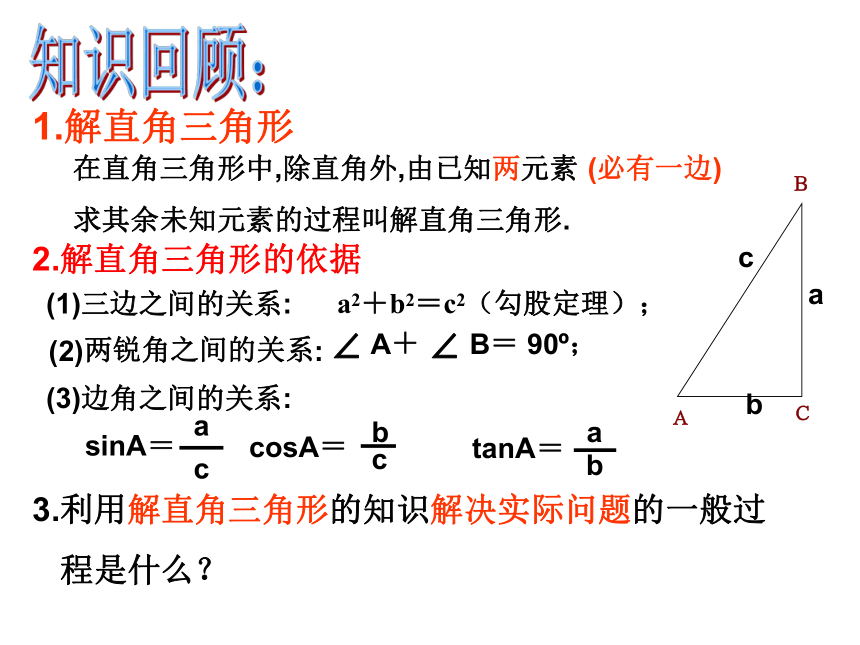
课件12张PPT。23.2解直角三角形的应用(3)在直角三角形中,除直角外,由已知两元素
求其余未知元素的过程叫解直角三角形.1.解直角三角形(1)三边之间的关系:a2+b2=c2(勾股定理);2.解直角三角形的依据(2)两锐角之间的关系:∠ A+ ∠ B= 90o;(3)边角之间的关系:sinA=知识回顾:(必有一边)3.利用解直角三角形的知识解决实际问题的一般过
程是什么?1.了解方位角的概念,利用解直角三角形的知识解决实际问题。
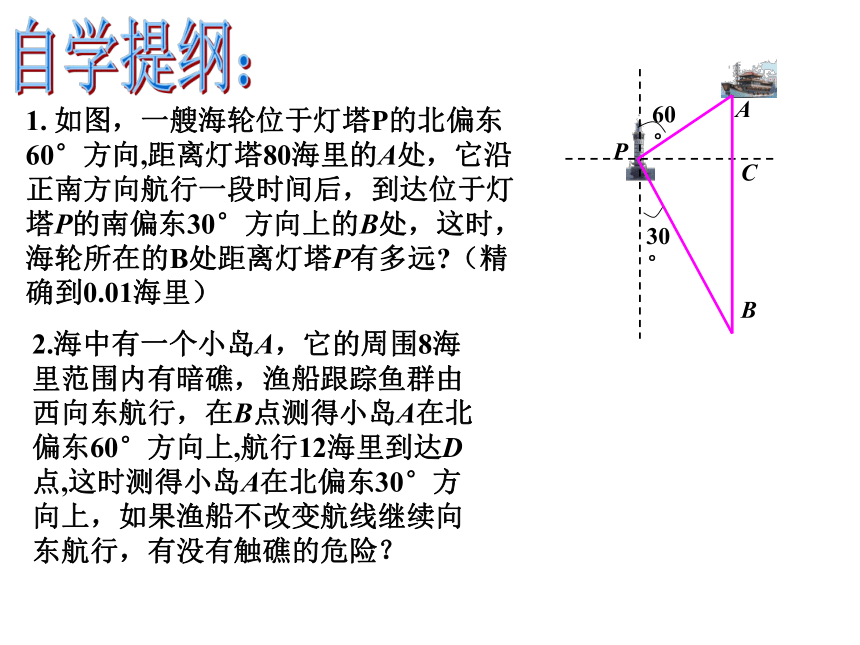
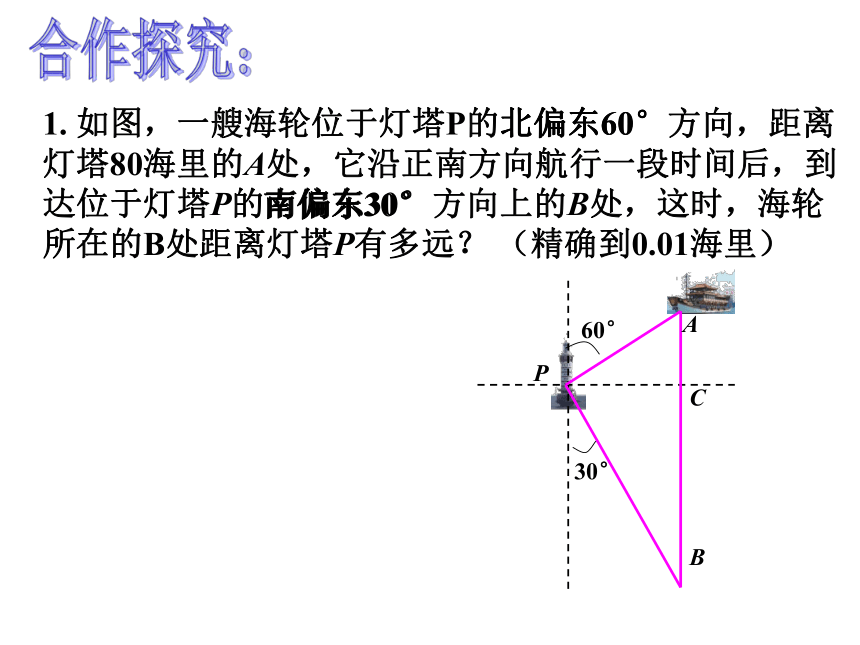
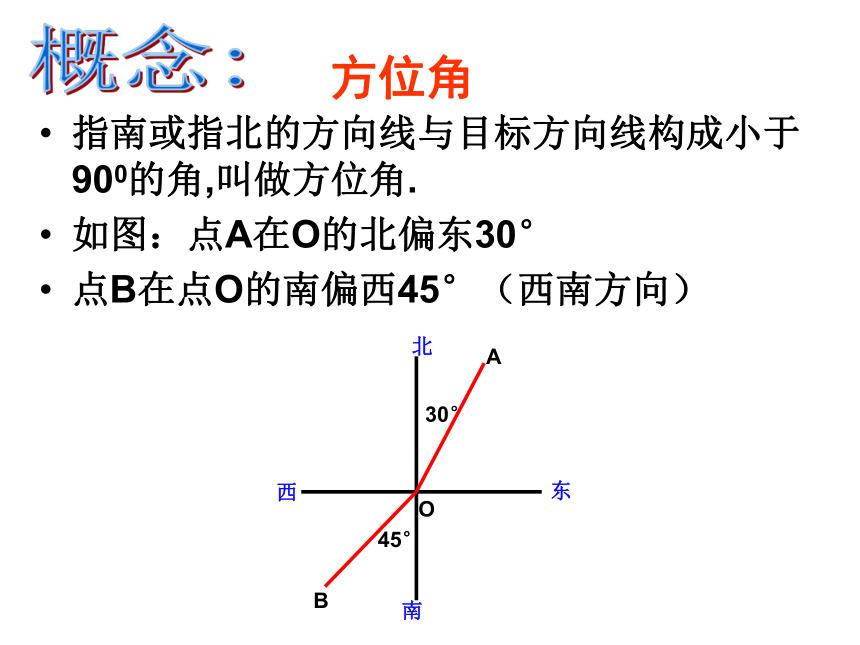
2.将某些实际问题中的数量关系,归结为直角三角形中元素之间的关系,从而解决问题。学习目标:自学提纲:1. 如图,一艘海轮位于灯塔P的北偏东60°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,这时,海轮所在的B处距离灯塔P有多远?(精确到0.01海里)2.海中有一个小岛A,它的周围8海里范围内有暗礁,渔船跟踪鱼群由西向东航行,在B点测得小岛A在北偏东60°方向上,航行12海里到达D点,这时测得小岛A在北偏东30°方向上,如果渔船不改变航线继续向东航行,有没有触礁的危险?1. 如图,一艘海轮位于灯塔P的北偏东60°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,这时,海轮所在的B处距离灯塔P有多远? (精确到0.01海里)合作探究:北偏东60°南偏东30°指南或指北的方向线与目标方向线构成小于900的角,叫做方位角.
如图:点A在O的北偏东30°
点B在点O的南偏西45°(西南方向)
方位角概念:例1. 如图,一艘海轮位于灯塔P的北偏东60°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,这时,海轮所在的B处距离灯塔P有多远? (精确到0.01海里)60°30°PBCA80合作探究:2.海中有一个小岛A,它的周围8海里范围内有暗礁,渔船跟踪鱼群由西向东航行,在B点测得小岛A在北偏东60°方向上,航行12海里到达D点,这时测得小岛A在北偏东30°方向上,如果渔船不改变航线继续向东航行,有没有触礁的危险?BAD60°1230° 某船向正东航行,在A处望见灯塔C在东北方向,前进到B处望见灯塔C在北偏西30°方向,又航行了半小时到达D处,望见灯塔C恰在西北方向,若船速为20海里/时,求A、B两点间的距离。(结果保留根号) C45°45°30°BDA理解应用: 1.在解直角三角形及应用时经常接触到的一些概念(方位角)
2.实际问题向数学模型的转化(解直角三角形)
知识小结: 1、凡是求线段的长的问题往往可以借助解直角三角形来解决,如果没有直角三角形可以设法去构造。
2、对于一些较复杂的问题,如果解一个直角三角形还不能使问题得以解决,可考虑解两个直角三角形。
3、如果不能直接通过解直角三角形处理问题, 可以去寻找已知与未知之间的等量关系,借助解直角三角形建立方程(组),从而使问题得以解决。
归纳:课堂作业:
必做题:课本128页 练习1,2。
选做题:课本131页 3
课外作业:基础训练 布置作业: 甲、乙两只渔船同时从O港出海捕鱼,甲船以15√2 km/h的速度沿北偏西60°方向前进,乙船以15km/h的速度沿东北方向前进,甲船航行2小时到达A处,此时甲船发现渔具丢在乙船上,于是甲船快速 (匀速)沿北偏东75°方向追赶,结果两船在B处相遇,甲船从A处追赶乙船用了多少时间?追赶速度是多少? C思考题:
求其余未知元素的过程叫解直角三角形.1.解直角三角形(1)三边之间的关系:a2+b2=c2(勾股定理);2.解直角三角形的依据(2)两锐角之间的关系:∠ A+ ∠ B= 90o;(3)边角之间的关系:sinA=知识回顾:(必有一边)3.利用解直角三角形的知识解决实际问题的一般过
程是什么?1.了解方位角的概念,利用解直角三角形的知识解决实际问题。
2.将某些实际问题中的数量关系,归结为直角三角形中元素之间的关系,从而解决问题。学习目标:自学提纲:1. 如图,一艘海轮位于灯塔P的北偏东60°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,这时,海轮所在的B处距离灯塔P有多远?(精确到0.01海里)2.海中有一个小岛A,它的周围8海里范围内有暗礁,渔船跟踪鱼群由西向东航行,在B点测得小岛A在北偏东60°方向上,航行12海里到达D点,这时测得小岛A在北偏东30°方向上,如果渔船不改变航线继续向东航行,有没有触礁的危险?1. 如图,一艘海轮位于灯塔P的北偏东60°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,这时,海轮所在的B处距离灯塔P有多远? (精确到0.01海里)合作探究:北偏东60°南偏东30°指南或指北的方向线与目标方向线构成小于900的角,叫做方位角.
如图:点A在O的北偏东30°
点B在点O的南偏西45°(西南方向)
方位角概念:例1. 如图,一艘海轮位于灯塔P的北偏东60°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,这时,海轮所在的B处距离灯塔P有多远? (精确到0.01海里)60°30°PBCA80合作探究:2.海中有一个小岛A,它的周围8海里范围内有暗礁,渔船跟踪鱼群由西向东航行,在B点测得小岛A在北偏东60°方向上,航行12海里到达D点,这时测得小岛A在北偏东30°方向上,如果渔船不改变航线继续向东航行,有没有触礁的危险?BAD60°1230° 某船向正东航行,在A处望见灯塔C在东北方向,前进到B处望见灯塔C在北偏西30°方向,又航行了半小时到达D处,望见灯塔C恰在西北方向,若船速为20海里/时,求A、B两点间的距离。(结果保留根号) C45°45°30°BDA理解应用: 1.在解直角三角形及应用时经常接触到的一些概念(方位角)
2.实际问题向数学模型的转化(解直角三角形)
知识小结: 1、凡是求线段的长的问题往往可以借助解直角三角形来解决,如果没有直角三角形可以设法去构造。
2、对于一些较复杂的问题,如果解一个直角三角形还不能使问题得以解决,可考虑解两个直角三角形。
3、如果不能直接通过解直角三角形处理问题, 可以去寻找已知与未知之间的等量关系,借助解直角三角形建立方程(组),从而使问题得以解决。
归纳:课堂作业:
必做题:课本128页 练习1,2。
选做题:课本131页 3
课外作业:基础训练 布置作业: 甲、乙两只渔船同时从O港出海捕鱼,甲船以15√2 km/h的速度沿北偏西60°方向前进,乙船以15km/h的速度沿东北方向前进,甲船航行2小时到达A处,此时甲船发现渔具丢在乙船上,于是甲船快速 (匀速)沿北偏东75°方向追赶,结果两船在B处相遇,甲船从A处追赶乙船用了多少时间?追赶速度是多少? C思考题:
