沪科版九年级数学上23.2解直角三角形的应用(4)--坡度课件(共15张PPT)
文档属性
| 名称 | 沪科版九年级数学上23.2解直角三角形的应用(4)--坡度课件(共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 762.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-01-03 10:07:49 | ||
图片预览



文档简介
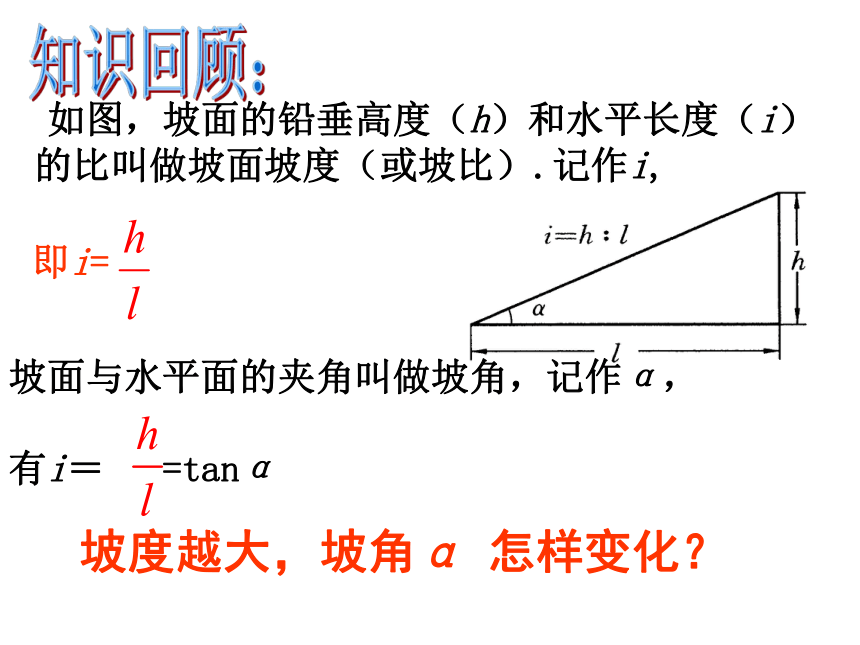
课件15张PPT。23.2解直角三角形的应用(4) 如图,坡面的铅垂高度(h)和水平长度(i)的比叫做坡面坡度(或坡比).记作i,
坡面与水平面的夹角叫做坡角,记作α,
有i= =tanα坡度越大,坡角α 怎样变化?即i=知识回顾:1.了解测量中坡度、坡角的概念,掌握坡度与坡角的关系,能利用解直角三角形的知识解决实际问题。
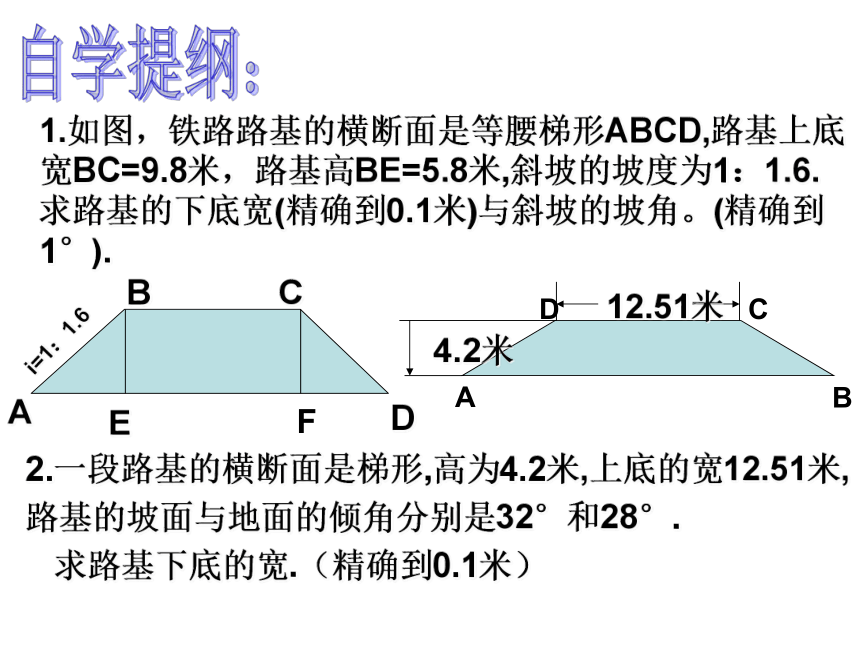
2.将某些实际问题中的数量关系,归结为直角三角形中元素之间的关系,从而解决问题。学习目标:自学提纲:1.如图,铁路路基的横断面是等腰梯形ABCD,路基上底宽BC=9.8米,路基高BE=5.8米,斜坡的坡度为1:1.6. 求路基的下底宽(精确到0.1米)与斜坡的坡角。(精确到1°). ?2.一段路基的横断面是梯形,高为4.2米,上底的宽12.51米,
路基的坡面与地面的倾角分别是32°和28°.
求路基下底的宽.(精确到0.1米) ?
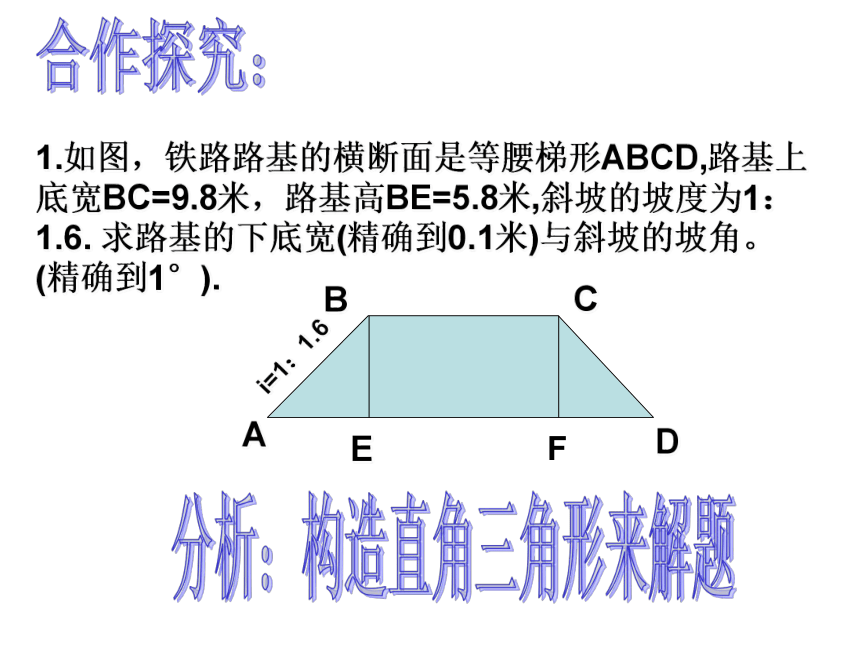
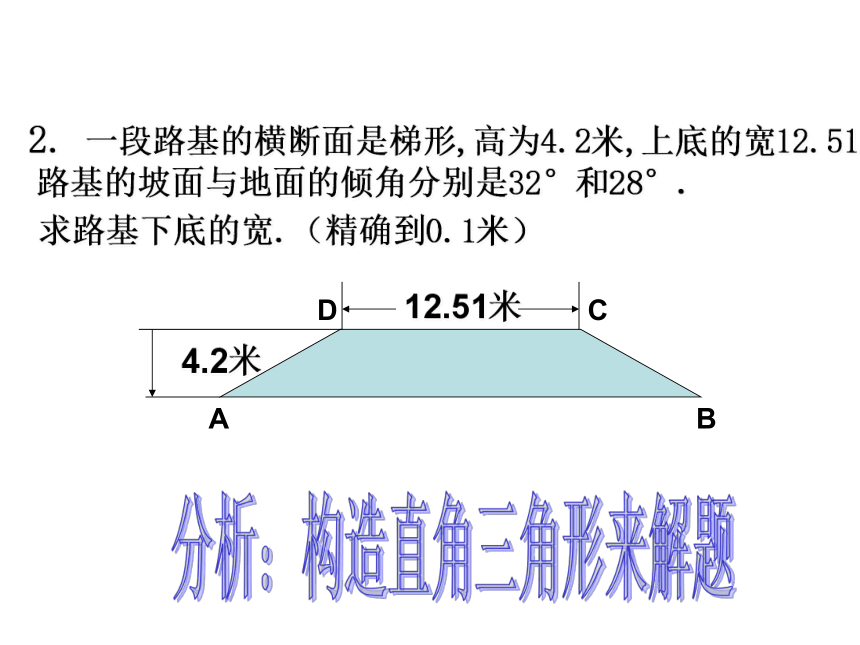
F1.如图,铁路路基的横断面是等腰梯形ABCD,路基上底宽BC=9.8米,路基高BE=5.8米,斜坡的坡度为1:1.6. 求路基的下底宽(精确到0.1米)与斜坡的坡角。(精确到1°). ?BCDAEi=1:1.6分析:构造直角三角形来解题合作探究:F 2. 一段路基的横断面是梯形,高为4.2米,上底的宽12.51米,路基的坡面与地面的倾角分别是32°和28°.
求路基下底的宽.(精确到0.1米) ?
分析:构造直角三角形来解题解 作DE⊥AB,CF⊥AB,垂足分别为E、F.由题意可知
DE=CF=4.2(米),
CD=EF=12.51(米).
在Rt△ADE中,因为
所以
在Rt△BCF中,同理可得
因此AB=AE+EF+BF ≈6.72+12.51+7.90≈27.13(米).
答: 路基下底的宽约为27.13米.
?1.一水库大坝的横断面为梯形ABCD,坝顶宽6米,坝高23米,斜坡AB的坡度i1=1∶3,斜坡CD的
坡度i2=1∶2.5.求:
(1)斜坡AB与坝底AD的长度;(精确到0.1米)
(2)斜坡CD的坡角α.(精确到1°)i1=1:3i2=1:2.5知识应用:2.如图,燕尾槽的横断面是等腰梯形。其中燕尾角∠B=55°,外口宽AD=180mm,燕尾槽的深度AE=70mm.求它的里口宽BC .(精确到1mm).3.一段河坝的断面为梯形ABCD,试根据图中数据,求出坡角α和坝底宽AD.
(单位米,结果保留根号)
?1.在解直角三角形及应用时经常接触到的一些概念(坡角、坡度) 知识小结:2.利用解直角三角形的知识解决实际问题的一般过程是:(1).将实际问题抽象为数学问题; (画出平面图形,转化为解直角三角形的问题)(2).根据条件的特点,适当选用锐角三角函数等去解直角三角形;(3).得到数学问题的答案;(4).得到实际问题的答案.课堂作业:
必做题:课本131页习题23.2 第5题
选做题:课本138页B组复习题 第6题
课外作业:基础训练
预习作业:本章小节与评价
填写第134至135主要知识回顾
A组复习题 1至8
B组复习题 1至3布置作业:See you 一个公共房屋门前的台阶共高出地面1.2米.台阶被拆除后,换成供轮椅行走的斜坡.根据这个城市的规定,轮椅行走斜坡的倾斜角不得超过9°.从斜坡的起点至楼门的最短的水平距离该是多少?(精确到0.1米)
知识应用:延伸拓展 某居民生活区有一块等腰梯形空地,经过测量得知,梯形上底与腰相等,下底是上底的2倍,现计划把这块空地分成形状和面积完全相同的四个部分,种上不同颜色的花草来美化环境,请你帮助设计出草图。
坡面与水平面的夹角叫做坡角,记作α,
有i= =tanα坡度越大,坡角α 怎样变化?即i=知识回顾:1.了解测量中坡度、坡角的概念,掌握坡度与坡角的关系,能利用解直角三角形的知识解决实际问题。
2.将某些实际问题中的数量关系,归结为直角三角形中元素之间的关系,从而解决问题。学习目标:自学提纲:1.如图,铁路路基的横断面是等腰梯形ABCD,路基上底宽BC=9.8米,路基高BE=5.8米,斜坡的坡度为1:1.6. 求路基的下底宽(精确到0.1米)与斜坡的坡角。(精确到1°). ?2.一段路基的横断面是梯形,高为4.2米,上底的宽12.51米,
路基的坡面与地面的倾角分别是32°和28°.
求路基下底的宽.(精确到0.1米) ?
F1.如图,铁路路基的横断面是等腰梯形ABCD,路基上底宽BC=9.8米,路基高BE=5.8米,斜坡的坡度为1:1.6. 求路基的下底宽(精确到0.1米)与斜坡的坡角。(精确到1°). ?BCDAEi=1:1.6分析:构造直角三角形来解题合作探究:F 2. 一段路基的横断面是梯形,高为4.2米,上底的宽12.51米,路基的坡面与地面的倾角分别是32°和28°.
求路基下底的宽.(精确到0.1米) ?
分析:构造直角三角形来解题解 作DE⊥AB,CF⊥AB,垂足分别为E、F.由题意可知
DE=CF=4.2(米),
CD=EF=12.51(米).
在Rt△ADE中,因为
所以
在Rt△BCF中,同理可得
因此AB=AE+EF+BF ≈6.72+12.51+7.90≈27.13(米).
答: 路基下底的宽约为27.13米.
?1.一水库大坝的横断面为梯形ABCD,坝顶宽6米,坝高23米,斜坡AB的坡度i1=1∶3,斜坡CD的
坡度i2=1∶2.5.求:
(1)斜坡AB与坝底AD的长度;(精确到0.1米)
(2)斜坡CD的坡角α.(精确到1°)i1=1:3i2=1:2.5知识应用:2.如图,燕尾槽的横断面是等腰梯形。其中燕尾角∠B=55°,外口宽AD=180mm,燕尾槽的深度AE=70mm.求它的里口宽BC .(精确到1mm).3.一段河坝的断面为梯形ABCD,试根据图中数据,求出坡角α和坝底宽AD.
(单位米,结果保留根号)
?1.在解直角三角形及应用时经常接触到的一些概念(坡角、坡度) 知识小结:2.利用解直角三角形的知识解决实际问题的一般过程是:(1).将实际问题抽象为数学问题; (画出平面图形,转化为解直角三角形的问题)(2).根据条件的特点,适当选用锐角三角函数等去解直角三角形;(3).得到数学问题的答案;(4).得到实际问题的答案.课堂作业:
必做题:课本131页习题23.2 第5题
选做题:课本138页B组复习题 第6题
课外作业:基础训练
预习作业:本章小节与评价
填写第134至135主要知识回顾
A组复习题 1至8
B组复习题 1至3布置作业:See you 一个公共房屋门前的台阶共高出地面1.2米.台阶被拆除后,换成供轮椅行走的斜坡.根据这个城市的规定,轮椅行走斜坡的倾斜角不得超过9°.从斜坡的起点至楼门的最短的水平距离该是多少?(精确到0.1米)
知识应用:延伸拓展 某居民生活区有一块等腰梯形空地,经过测量得知,梯形上底与腰相等,下底是上底的2倍,现计划把这块空地分成形状和面积完全相同的四个部分,种上不同颜色的花草来美化环境,请你帮助设计出草图。
