沪科版七年级上第四章直线与角期末复习课件(共77张)
文档属性
| 名称 | 沪科版七年级上第四章直线与角期末复习课件(共77张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-01-03 00:00:00 | ||
图片预览


文档简介
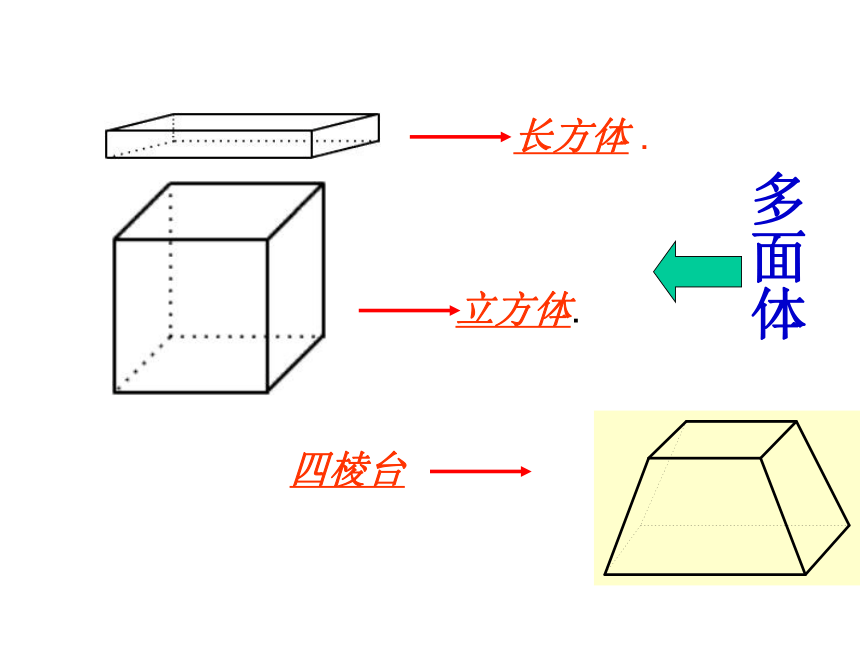
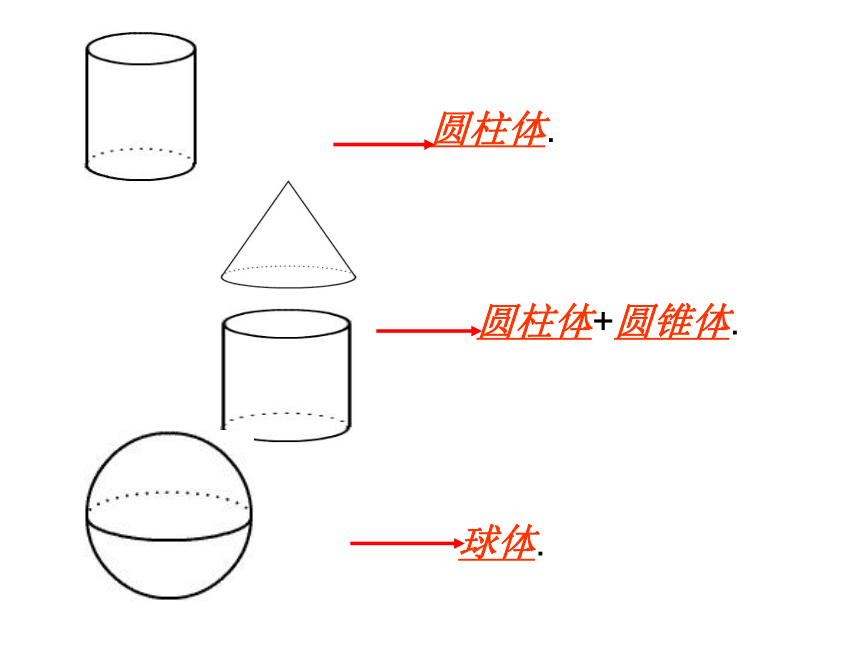
课件77张PPT。几何图形只考虑物体的
形状、大小、位置,
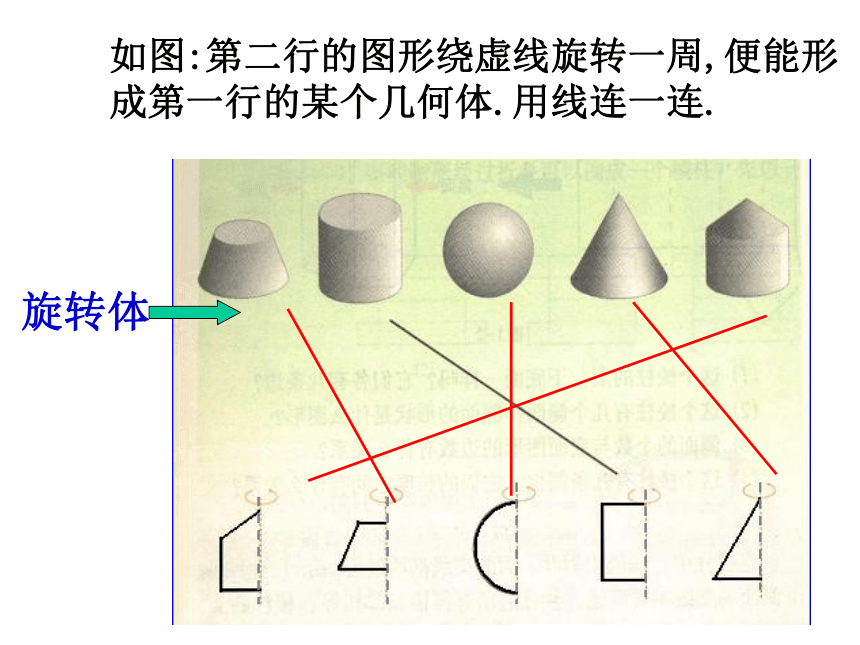
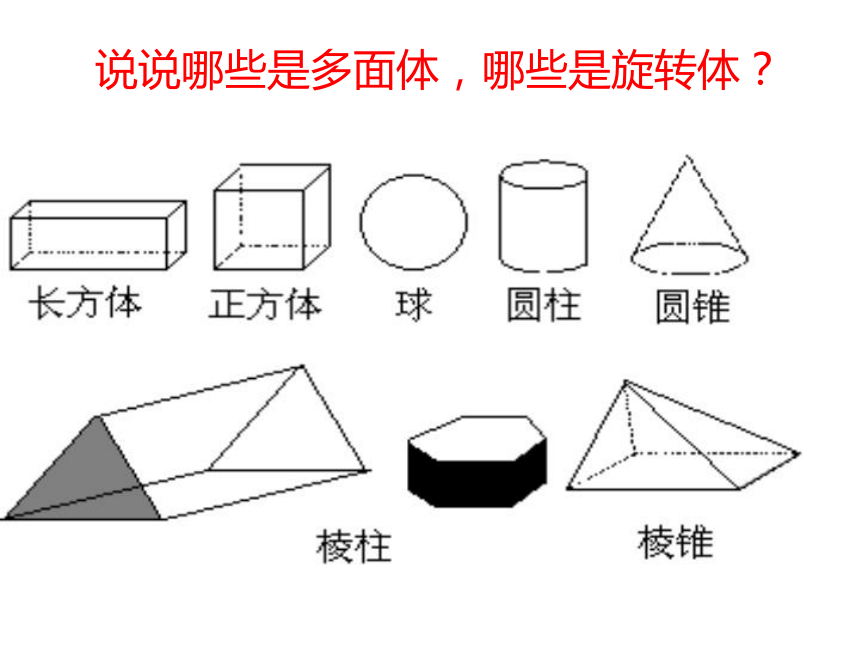
不考虑颜色、重量、材料四棱台如图:第二行的图形绕虚线旋转一周,便能形成第一行的某个几何体.用线连一连. 说说哪些是多面体,哪些是旋转体? 几何图形:
(点,线,面,体) 体由面围成,
面与面相交成线,线与线相交成点.
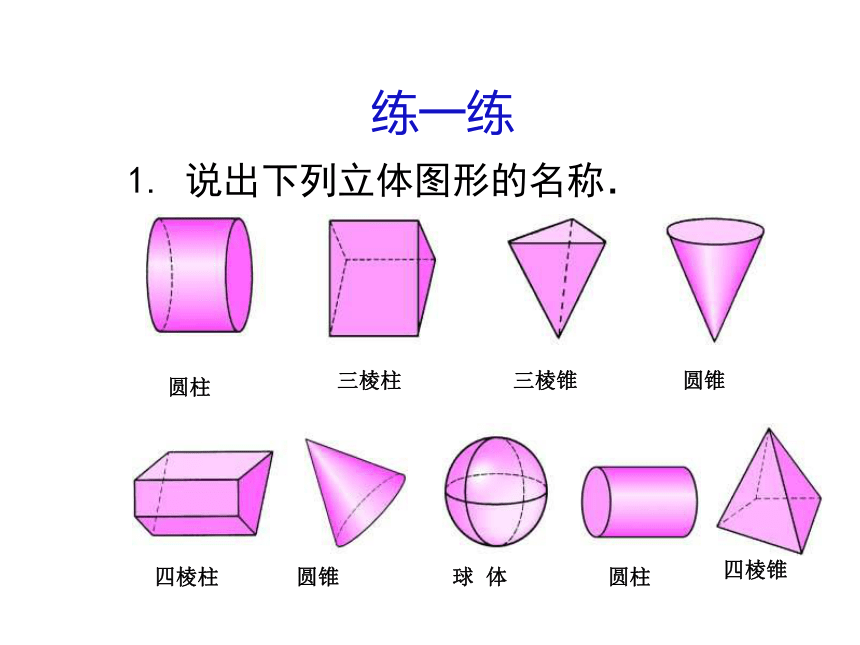
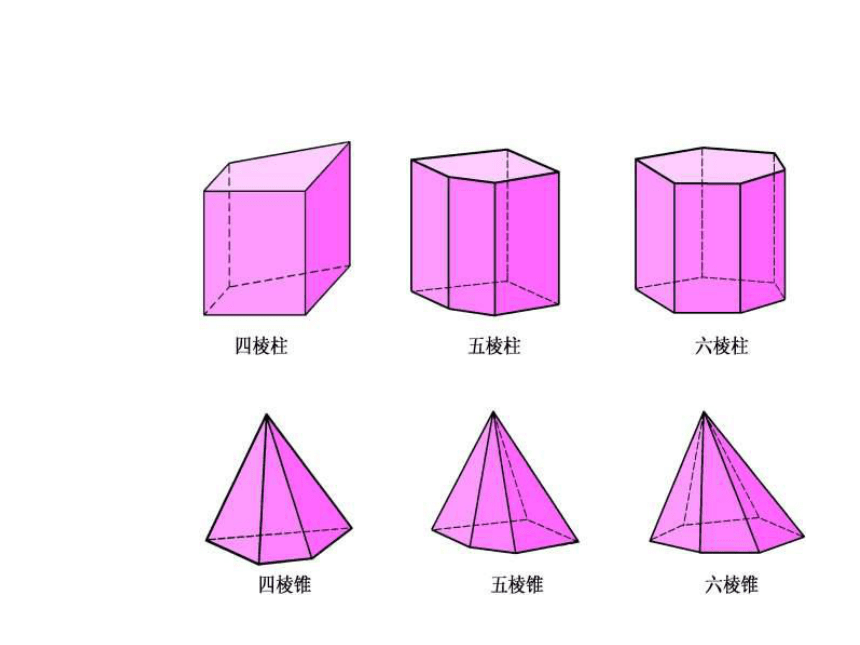
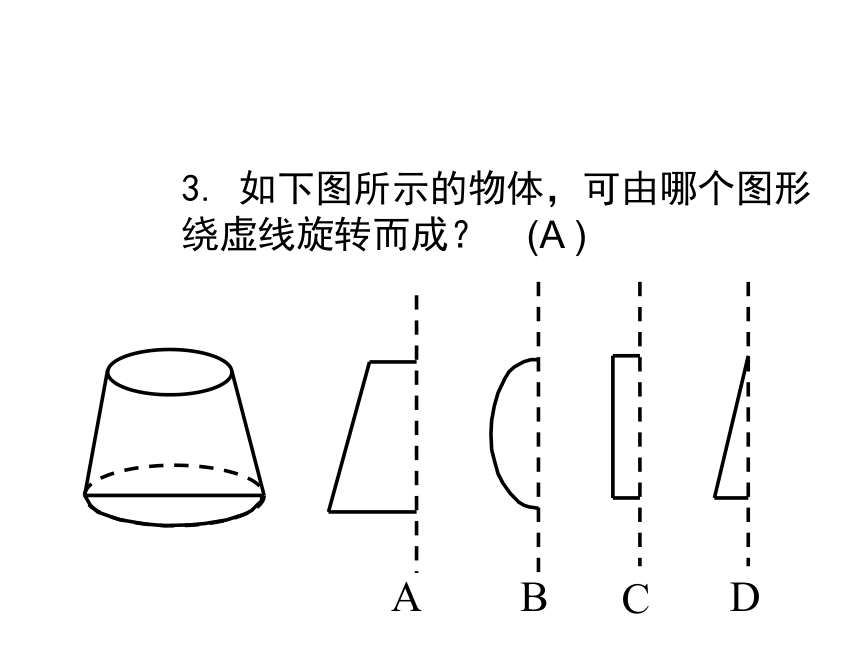
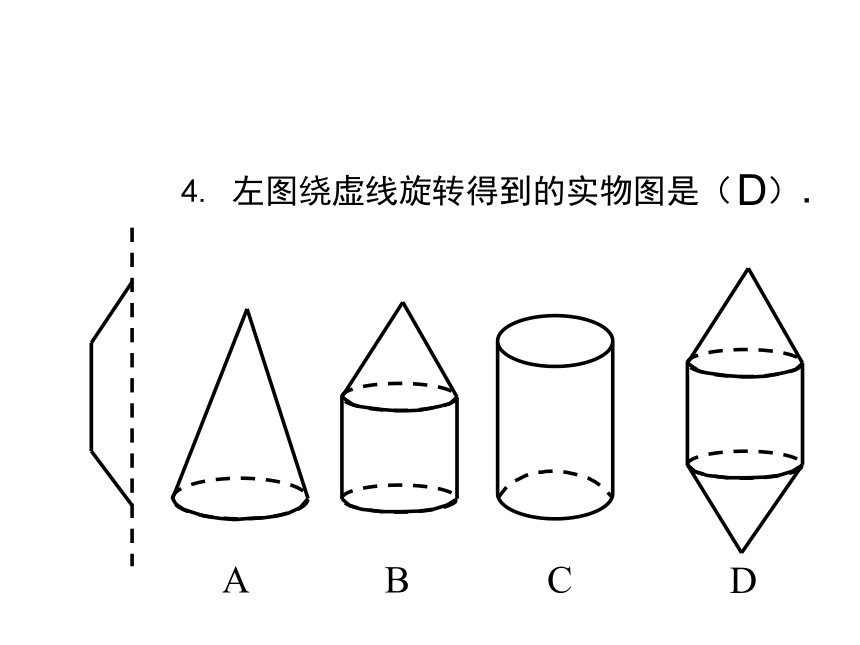
点运动成线,线运动成面,面运动成体。1. 说出下列立体图形的名称. 练一练圆柱三棱柱三棱锥圆锥四棱柱圆锥球 体圆柱四棱锥3. 如下图所示的物体,可由哪个图形绕虚线旋转而成?ABCD(A )4. 左图绕虚线旋转得到的实物图是( ).ABCDD圆柱长方体棱柱圆锥练习:立方体的平面展开图 下面六个正方形连在一起的图形,经折叠后能围成正方体的图形有哪几个?(动手试试)G试一试从不同方向看物体 竖琴中紧绷的琴弦,马路上人行横道都可以近似的看做线段。★ 线段有两个端点 由手电筒射出的光,流星划过天空留下的痕迹,导弹发射后留下的白烟,我们可以把它看作一条一端无限延伸的线。★ 射线有一个端点将线段向一个方向无限延长形成了射线
笔直的铁轨向两个方向无限延长★ 直线没有端点将线段向两个方向无限延长形成了直线(1)线段:
(2) 射线:(3) 直线: l 想一想 线段、射线、直线的联系和区别?联系:都是直的,线段向一个方向延长可以得
到射线, 线段向两个方向延长可以得到
直线。由此可知, 射线、线段都是直线
的一部分。线段是射线的一部分。区别:直线可以向两个方向无限延伸,射线可
以向一个方向延伸,线段本身不能延伸。
直线没有端点,射线有一个端点,线段
有两个端点。想一想(1) 过一点 A 可以画几条直线?●A(2) 过两点A、B可以画几条直线?●●AB(3) 如果你想将一根细木条固定在墙上,
至少需要几个钉子?经过两点有且只有一条直线(2) 手电筒射出的的光线是 ,其特点是 。填一填:(1) 长方形的棱 , 其特点是 。(3) 笔直的,并向两个方向无限延伸的铁轨可以看成 。
其特点是 。线段 有两个端点 射线只有一个端点直线没有端点无数一判断:
1.一条线段上有两个点。( )
2.射线BA和射线AB是同一条射线。( )
3.在直线上取一点可以形成两条射线。( )
4.直线的一部分是线段。( )
5.在射线上取一点可以得到两条射线(包括原来的射线)和一条线段。( )
6.连结两点间的线段,叫做两点的距离。( )
7.射线是直线的一半。( )
8.延长直线AB。( )
9.在直线l上依次取A、B、C三点,则以A为端点的射线有两条,即射线AB和射线AC。( )
10.在直线上依次取A、B、C、D四,B为AC中点,C为AD中点,则AB=1/2CD( )
11.如果线段AB=5cm,BC=3cm,则A,C两点的距离是8㎝或2㎝。( )
12.两点确定一条直线,三点确定三条直线。( )
13.三条直线两两相交有三个交点。( )
14. A、B是直线上任意两点,P是直线外一点,连结PA、PB,则PA+PB>AB。 ( )
15.如果线段MN=7厘米,MP=4厘米,NP=3厘米,那么M,P,N在同一条直线上。( )
如图从A村到B村,有三条路径可选择你愿意选第几条路径?说出你的理由。 你会选吗1、线段公理:两点之间的所有连线中,线段最短。即两点之间线段最短 2、两点间的距离:连接两点的线段的长度,叫这两点间的距离。(2)如图:这是A、B两地之间的公路,在公路工程改造计划时,为使A、B两地行程最短,应如何设计线路?在图中画出。你的理由是
_______________________________练一练长度两点之间线段最短(1)判断:两点之间的距离是指两点之间的线段 的 ( ) l 3、线段的中点 ?你如何确定一条线段的中点 如图:点M把线段AB分成相等的两条线段AM与BM,点M叫做线段AB的
中点。这时AM=BM= AB或AB=2AM=2BM4、线段的比较大小:
想一想:如何比较两条线段的大小叠合法度量法AB﹥CDAB=CDAB﹤CD第一步:先用直尺画一条射线AB第二步:用圆规量出已知线段的长度第三步:在射线AB上A以为圆心,截
取AC=a结论:线段AC就是所求的线段5、线段的和差及画法(1)如图,AD=AB—____=AC+ _____BDCD试一试(2)如图 AB=6cm,点C是AB的中点,点D是CB的中点,则AD=____cm(3)如图,下列说法 ,不能判断点C是线段AB的中点的是( )
A、AC=CB B、AB=2AC
C、AC+CB=AB D、CB= AB C4.5回顾要点:1.线段的基本性质:两点之间线段最短。2.两点之间的距离:两点之间线段的长度。3.线段的两种比较方法:叠合法和度量法。4.线段的中点的概念及表示方法。
四、角 的 度 量 和 表 示
ABC...Back有公共端点的两条射线组成的图形.两条射线的公共端点是这个角的顶点.两条射线是这个角的两条边.1、角的概念:1、说出下列各图中角的顶点和角的两边.(1)(3)(2)1.用三个大写字母及符号“∠”来表示.2、角的表示方法:
2.用一个数字及符号“∠”来表示
∠ABC∠1或∠αα 3.用一个希腊字母及符号“∠” 来表示.
4.用顶点字母及符号“∠”来表示.
或∠B
试一试:⑴⑵用适当方法分别表示下图中的每个角∠BAC 或 ∠A∠BAC , ∠CAD ,∠BAD方位角:用来确定方向
一般是南北偏东西1.如图,下列说法错误的是( )
(A)?? D点在O点的东南方向
(B)?? C点在O点的正南方向
(C)?? B点在O点的西偏北30°
(D) A点在O点的北偏东60°
2.点A在点B的正北方,则点B在点
A的 ,点C在点D的北偏西300,
则点B在点A的 .
例:计算
(1) 1.45°等于多少分?等于多少秒?
(2) 2400″等于多少分?等于多少度?
(3) 3.58°+ 7°24′30″1度=60分
1分=60秒
1秒= 分
1秒= 度
角的度量:量角器度、分、秒
1度=60分,1分=60秒
(1/12)°=( )′=( )″
48″=( )′=( )°
(3) 82.13°= 度 分 秒. 角的分类:
锐角、直角、钝角、平角、周角
1平角= 直角= 度,1/2周角= 直角= 度 五、角的比较你选择从哪一面上山呢?成功永远属于肯攀高峰的人∠ABC>∠DCB锐角:900>α>00钝角:1800> α>900 周角>平角>钝角>直角>锐角1平角=18001直角=9001周角=3600(一). 用量角器测量角的度数方法 :1、对“中”—角的顶点对量角器的中心3、读数—读出角的另一边所对的度数2、重合—角的一边与量角器的零线重合BCA700300∠ABC > ∠DEF1. 将两个角的顶点及一边重合2. 两个角的另一边落在重合一边的同侧3.由两个角的另一边的位置确定两个角的大小(二). 叠合法∠ECD>∠AOB∠ECD<∠AOB∠ECD=∠AOB∠2= ∠1+∠3∠3= ∠2- ∠1∠1= ∠2-∠3(三). 角的和差3⌒一条射线把一个角分成两个相等的角,则这条射线叫这个角的角平分线。⌒⌒31OACB符号语言∵∠1=∠3 (或∠AOB= 2∠1 , ∠AOB= 2∠3)
∴射线OC平分∠AOB∵射线OC平分∠AOB
∴∠1=∠3 问题:(1)在放大镜下,一个角的度数变大了吗?(2)角的两边的长短与角的大小有关吗?如图∠ AOC = ( ) + ( )
= ( ) - ( )∠ BOC=( ) - ( )
= ( ) -( )∠ AOB∠ BOC∠ AOD∠ COD∠ COD∠ BOD∠ AOC∠ AOB 如图∠ AOB= ∠ COD=900, ∠ AOD=1460, ∠ BOC= ; 340思考:
当∠BOA= 2∠1时,
∠1、∠3是什么关系? 2、按图填空: (1)∠ABC= ∠ABD+(2)∠ADB= ∠ADC-3、BD是∠ABC的平分线,那么(1)∠ABD= ∠(2)∠ = 2∠DBCDBCABC∠DBC∠BDCDABC已知: ∠ AOB=760,OC为∠ AOB的角平分线,
那么∠ AOC= , ∠ AOC= ∠ AOB,
∠ AOB= ∠ COB3802 下面的式子中,能表示“OC是
∠ AOB的平分线”的等式是( )A、2 ∠ AOC= ∠ BOCB、∠ AOC= ∠ AOBC、∠ AOB=2 ∠ BOCD、∠ AOC= ∠ BOC给出你的选择:D 图中∠1= ∠2, 试判断∠BAD和
∠EAC的大小, 并说明理由.冲击1、作一条线段等于已知线段已知:线段a.
求作:线段AB,使AB=a.作法:以a的长为半径画弧, AB 就是所求作的线段。这种只用没有刻度的直尺和圆规作图的方法叫尺规作图已知: ∠AOB.作一个角等于已知角求作: ∠DEF 使∠DEF=∠AOB.(1) 以点O为圆心,任意长为半径交OA于点P, (3) 以点E为圆心,画弧, PQ同样长(OP) 为半径画弧, D(4) 以点D为圆心,PQ长为半径画弧, F(5) 作射线EF.∠DEF就是所求作的角.(2) 作射线EG;已知: ∠AOB。求作: ∠A’O’B’ ,使∠A’O’B’=2∠AOB。作法一:∠A’O’B’为所求.∠A’O’B’为所求.
形状、大小、位置,
不考虑颜色、重量、材料四棱台如图:第二行的图形绕虚线旋转一周,便能形成第一行的某个几何体.用线连一连. 说说哪些是多面体,哪些是旋转体? 几何图形:
(点,线,面,体) 体由面围成,
面与面相交成线,线与线相交成点.
点运动成线,线运动成面,面运动成体。1. 说出下列立体图形的名称. 练一练圆柱三棱柱三棱锥圆锥四棱柱圆锥球 体圆柱四棱锥3. 如下图所示的物体,可由哪个图形绕虚线旋转而成?ABCD(A )4. 左图绕虚线旋转得到的实物图是( ).ABCDD圆柱长方体棱柱圆锥练习:立方体的平面展开图 下面六个正方形连在一起的图形,经折叠后能围成正方体的图形有哪几个?(动手试试)G试一试从不同方向看物体 竖琴中紧绷的琴弦,马路上人行横道都可以近似的看做线段。★ 线段有两个端点 由手电筒射出的光,流星划过天空留下的痕迹,导弹发射后留下的白烟,我们可以把它看作一条一端无限延伸的线。★ 射线有一个端点将线段向一个方向无限延长形成了射线
笔直的铁轨向两个方向无限延长★ 直线没有端点将线段向两个方向无限延长形成了直线(1)线段:
(2) 射线:(3) 直线: l 想一想 线段、射线、直线的联系和区别?联系:都是直的,线段向一个方向延长可以得
到射线, 线段向两个方向延长可以得到
直线。由此可知, 射线、线段都是直线
的一部分。线段是射线的一部分。区别:直线可以向两个方向无限延伸,射线可
以向一个方向延伸,线段本身不能延伸。
直线没有端点,射线有一个端点,线段
有两个端点。想一想(1) 过一点 A 可以画几条直线?●A(2) 过两点A、B可以画几条直线?●●AB(3) 如果你想将一根细木条固定在墙上,
至少需要几个钉子?经过两点有且只有一条直线(2) 手电筒射出的的光线是 ,其特点是 。填一填:(1) 长方形的棱 , 其特点是 。(3) 笔直的,并向两个方向无限延伸的铁轨可以看成 。
其特点是 。线段 有两个端点 射线只有一个端点直线没有端点无数一判断:
1.一条线段上有两个点。( )
2.射线BA和射线AB是同一条射线。( )
3.在直线上取一点可以形成两条射线。( )
4.直线的一部分是线段。( )
5.在射线上取一点可以得到两条射线(包括原来的射线)和一条线段。( )
6.连结两点间的线段,叫做两点的距离。( )
7.射线是直线的一半。( )
8.延长直线AB。( )
9.在直线l上依次取A、B、C三点,则以A为端点的射线有两条,即射线AB和射线AC。( )
10.在直线上依次取A、B、C、D四,B为AC中点,C为AD中点,则AB=1/2CD( )
11.如果线段AB=5cm,BC=3cm,则A,C两点的距离是8㎝或2㎝。( )
12.两点确定一条直线,三点确定三条直线。( )
13.三条直线两两相交有三个交点。( )
14. A、B是直线上任意两点,P是直线外一点,连结PA、PB,则PA+PB>AB。 ( )
15.如果线段MN=7厘米,MP=4厘米,NP=3厘米,那么M,P,N在同一条直线上。( )
如图从A村到B村,有三条路径可选择你愿意选第几条路径?说出你的理由。 你会选吗1、线段公理:两点之间的所有连线中,线段最短。即两点之间线段最短 2、两点间的距离:连接两点的线段的长度,叫这两点间的距离。(2)如图:这是A、B两地之间的公路,在公路工程改造计划时,为使A、B两地行程最短,应如何设计线路?在图中画出。你的理由是
_______________________________练一练长度两点之间线段最短(1)判断:两点之间的距离是指两点之间的线段 的 ( ) l 3、线段的中点 ?你如何确定一条线段的中点 如图:点M把线段AB分成相等的两条线段AM与BM,点M叫做线段AB的
中点。这时AM=BM= AB或AB=2AM=2BM4、线段的比较大小:
想一想:如何比较两条线段的大小叠合法度量法AB﹥CDAB=CDAB﹤CD第一步:先用直尺画一条射线AB第二步:用圆规量出已知线段的长度第三步:在射线AB上A以为圆心,截
取AC=a结论:线段AC就是所求的线段5、线段的和差及画法(1)如图,AD=AB—____=AC+ _____BDCD试一试(2)如图 AB=6cm,点C是AB的中点,点D是CB的中点,则AD=____cm(3)如图,下列说法 ,不能判断点C是线段AB的中点的是( )
A、AC=CB B、AB=2AC
C、AC+CB=AB D、CB= AB C4.5回顾要点:1.线段的基本性质:两点之间线段最短。2.两点之间的距离:两点之间线段的长度。3.线段的两种比较方法:叠合法和度量法。4.线段的中点的概念及表示方法。
四、角 的 度 量 和 表 示
ABC...Back有公共端点的两条射线组成的图形.两条射线的公共端点是这个角的顶点.两条射线是这个角的两条边.1、角的概念:1、说出下列各图中角的顶点和角的两边.(1)(3)(2)1.用三个大写字母及符号“∠”来表示.2、角的表示方法:
2.用一个数字及符号“∠”来表示
∠ABC∠1或∠αα 3.用一个希腊字母及符号“∠” 来表示.
4.用顶点字母及符号“∠”来表示.
或∠B
试一试:⑴⑵用适当方法分别表示下图中的每个角∠BAC 或 ∠A∠BAC , ∠CAD ,∠BAD方位角:用来确定方向
一般是南北偏东西1.如图,下列说法错误的是( )
(A)?? D点在O点的东南方向
(B)?? C点在O点的正南方向
(C)?? B点在O点的西偏北30°
(D) A点在O点的北偏东60°
2.点A在点B的正北方,则点B在点
A的 ,点C在点D的北偏西300,
则点B在点A的 .
例:计算
(1) 1.45°等于多少分?等于多少秒?
(2) 2400″等于多少分?等于多少度?
(3) 3.58°+ 7°24′30″1度=60分
1分=60秒
1秒= 分
1秒= 度
角的度量:量角器度、分、秒
1度=60分,1分=60秒
(1/12)°=( )′=( )″
48″=( )′=( )°
(3) 82.13°= 度 分 秒. 角的分类:
锐角、直角、钝角、平角、周角
1平角= 直角= 度,1/2周角= 直角= 度 五、角的比较你选择从哪一面上山呢?成功永远属于肯攀高峰的人∠ABC>∠DCB锐角:900>α>00钝角:1800> α>900 周角>平角>钝角>直角>锐角1平角=18001直角=9001周角=3600(一). 用量角器测量角的度数方法 :1、对“中”—角的顶点对量角器的中心3、读数—读出角的另一边所对的度数2、重合—角的一边与量角器的零线重合BCA700300∠ABC > ∠DEF1. 将两个角的顶点及一边重合2. 两个角的另一边落在重合一边的同侧3.由两个角的另一边的位置确定两个角的大小(二). 叠合法∠ECD>∠AOB∠ECD<∠AOB∠ECD=∠AOB∠2= ∠1+∠3∠3= ∠2- ∠1∠1= ∠2-∠3(三). 角的和差3⌒一条射线把一个角分成两个相等的角,则这条射线叫这个角的角平分线。⌒⌒31OACB符号语言∵∠1=∠3 (或∠AOB= 2∠1 , ∠AOB= 2∠3)
∴射线OC平分∠AOB∵射线OC平分∠AOB
∴∠1=∠3 问题:(1)在放大镜下,一个角的度数变大了吗?(2)角的两边的长短与角的大小有关吗?如图∠ AOC = ( ) + ( )
= ( ) - ( )∠ BOC=( ) - ( )
= ( ) -( )∠ AOB∠ BOC∠ AOD∠ COD∠ COD∠ BOD∠ AOC∠ AOB 如图∠ AOB= ∠ COD=900, ∠ AOD=1460, ∠ BOC= ; 340思考:
当∠BOA= 2∠1时,
∠1、∠3是什么关系? 2、按图填空: (1)∠ABC= ∠ABD+(2)∠ADB= ∠ADC-3、BD是∠ABC的平分线,那么(1)∠ABD= ∠(2)∠ = 2∠DBCDBCABC∠DBC∠BDCDABC已知: ∠ AOB=760,OC为∠ AOB的角平分线,
那么∠ AOC= , ∠ AOC= ∠ AOB,
∠ AOB= ∠ COB3802 下面的式子中,能表示“OC是
∠ AOB的平分线”的等式是( )A、2 ∠ AOC= ∠ BOCB、∠ AOC= ∠ AOBC、∠ AOB=2 ∠ BOCD、∠ AOC= ∠ BOC给出你的选择:D 图中∠1= ∠2, 试判断∠BAD和
∠EAC的大小, 并说明理由.冲击1、作一条线段等于已知线段已知:线段a.
求作:线段AB,使AB=a.作法:以a的长为半径画弧, AB 就是所求作的线段。这种只用没有刻度的直尺和圆规作图的方法叫尺规作图已知: ∠AOB.作一个角等于已知角求作: ∠DEF 使∠DEF=∠AOB.(1) 以点O为圆心,任意长为半径交OA于点P, (3) 以点E为圆心,画弧, PQ同样长(OP) 为半径画弧, D(4) 以点D为圆心,PQ长为半径画弧, F(5) 作射线EF.∠DEF就是所求作的角.(2) 作射线EG;已知: ∠AOB。求作: ∠A’O’B’ ,使∠A’O’B’=2∠AOB。作法一:∠A’O’B’为所求.∠A’O’B’为所求.
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
