高中数学 必修1 第二章 基本初等函数(Ⅰ) 复习+练习
文档属性
| 名称 | 高中数学 必修1 第二章 基本初等函数(Ⅰ) 复习+练习 |  | |
| 格式 | zip | ||
| 文件大小 | 426.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-01-03 07:22:50 | ||
图片预览


文档简介
第二章
基本初等函数(Ⅰ)
一、指数与指数幂的运算
1.根式的概念
①如果,且,那么叫做的次方根.当是奇数时,的次方根用符号表示;当是偶数时,正数的正的次方根用符号表示,负的次方根用符号表示;0的次方根是0;负数没有次方根.
②式子叫做根式,这里叫做根指数,叫做被开方数.当为奇数时,为任意实数;当为偶数时,.
③根式的性质:;当为奇数时,;当为偶数时,
.
2.分数指数幂的概念
①正数的正分数指数幂的意义是:且.0的正分数指数幂等于0.
②正数的负分数指数幂的意义是:且.0的负分数指数幂没有意义.注意口诀:底数取倒数,指数取相反数.
3.指数幂的运算性质
①
②
③
例1
化简:(1);
(2)(a>0,b>0);
(3).
解:(1)原式=.
(2)原式====.
(3)原式=.
点评:根式化分数指数幂时,切记不能混淆,注意将根指数化为分母,幂指数化为分子,根号的嵌套,化为幂的幂.正确转化和运用幂的运算性质,是复杂根式化简的关键.
例2
化简与求值:
(1);
(2).
解:(1)原式=
=
==4.
(2)原式=
==.
点评:形如的双重根式,当是一个平方数时,则能通过配方法去掉双重根号,这也是双重根号能否开方的判别技巧.
而分母有理化中,常常用到的是平方差公式,第(2)小题也体现了一种消去法的思想.
第(1)小题还可用平方法,即先算得原式的平方,再开方而得.
二、指数函数及其性质
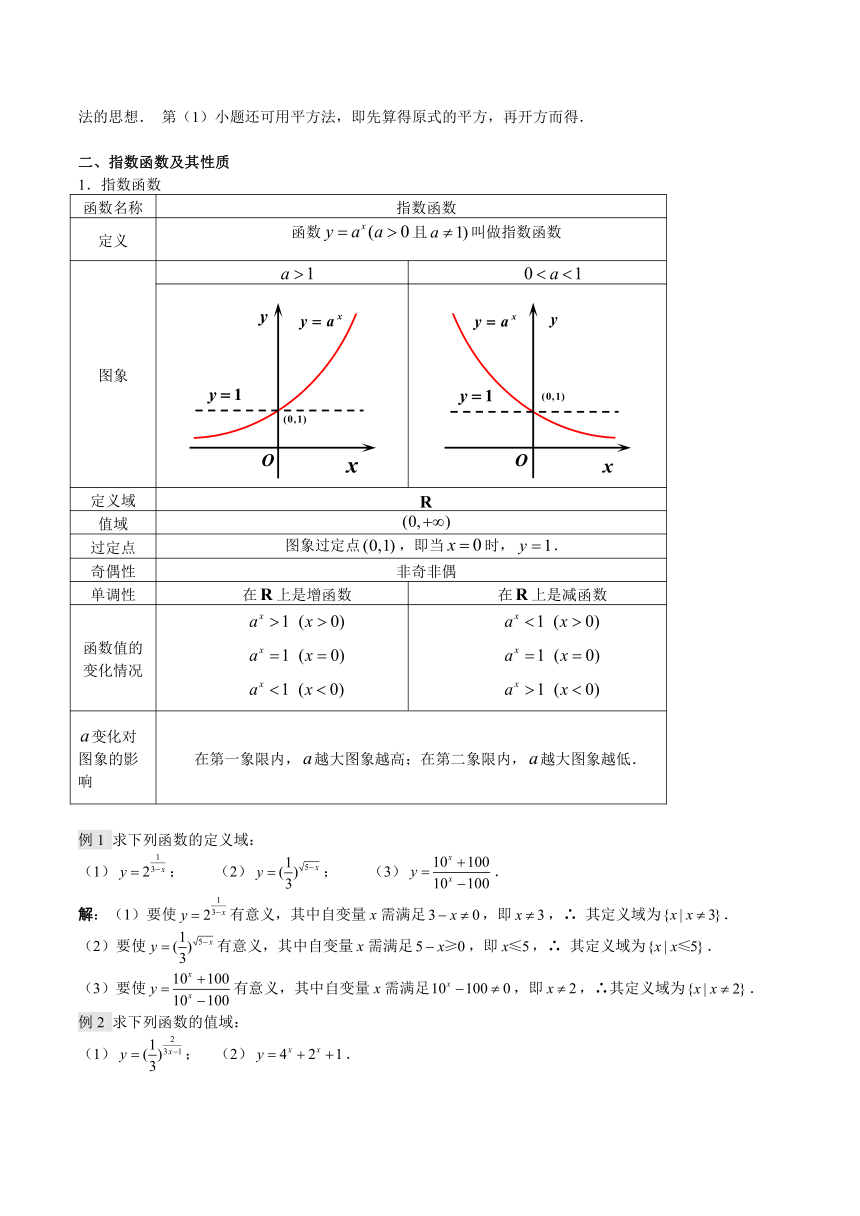
1.指数函数
函数名称
指数函数
定义
函数且叫做指数函数
图象
定义域
值域
过定点
图象过定点,即当时,.
奇偶性
非奇非偶
单调性
在上是增函数
在上是减函数
函数值的变化情况
变化对图象的影响
在第一象限内,越大图象越高;在第二象限内,越大图象越低.
例1
求下列函数的定义域:
(1);
(2);
(3).
解:(1)要使有意义,其中自变量x需满足,即,∴
其定义域为.
(2)要使有意义,其中自变量x需满足,即,∴
其定义域为.
(3)要使有意义,其中自变量x需满足,即,∴其定义域为.
例2
求下列函数的值域:
(1);
(2).
解:(1)观察易知,
则有.
∴
原函数的值域为.
(2).
令,易知.
则.
结合二次函数的图象,由其对称轴观察得到在上为增函数,
所以.
∴
原函数的值域为.
例3
函数的图象如图,其中a、b为常数,则下列结论正确的是(
).
A.
B.
C.
D.
解:从曲线的变化趋势,可以得到函数为减函数,从而0<a<1;从曲线位置看,是由函数的图象向左平移|-b|个单位而得,所以-b>0,即b<0.
所以选D.
点评:观察图象变化趋势,得到函数的单调性,结合指数函数的单调性,得到参数a的范围.
根据所给函数式的平移变换规律,得到参数b的范围.
也可以取x=1时的特殊点,得到,从而b<0.
例4
已知.
(1)讨论的奇偶性;
(2)讨论的单调性.
解:(1)的定义域为R.
∵
.
∴
为奇函数.
(2)设任意,且,则
.
由于,从而,即.
∴
,即,
∴
为增函数.
点评:在这里,奇偶性与单调性的判别,都是直接利用知识的定义来解决.需要我们理解两个定义,掌握其运用的基本模式,并能熟练的进行代数变形,得到理想中的结果.
例5
求下列函数的单调区间:(1);
(2).
解:(1)设.
由知,在上为减函数,在上为增函数.
根据的单调性,当时,y关于u为增函数;当时,y关于u为减函数.
∴
当时,原函数的增区间为,减区间为;
当时,原函数的增区间为,减区间为.
(2)函数的定义域为.
设.
易知为减函数.
而根据的图象可以得到,在区间与上,y关于u均为减函数.
∴在上,原函数为增函数;在上,原函数也为增函数.
点评:研究形如的函数的单调性,可以有如下结论:当时,函数的单调性与的单调性相同;当时,函数的单调性与的单调性相反.
而对于形如的函数单调性的研究,也需结合的单调性及的单调性进行研究.
复合函数的单调性研究,遵循一般步骤和结论,即:分别求出与两个函数的单调性,再按口诀“同增异减”得出复合后的单调性,即两个函数同为增函数或者同为减函数,则复合后结果为增函数;若两个函数一增一减,则复合后结果为减函数.为何有“同增异减”?我们可以抓住
“x的变化→的变化→的变化”这样一条思路进行分析.
三、对数与对数运算
1.对数的定义
①若,则叫做以为底的对数,记作,其中叫做对数的底数,叫做真数.
②负数和零没有对数.
③对数式与指数式的互化:.
2.几个重要的对数恒等式
,,.
3.常用对数与自然对数
常用对数:,即;自然对数:,即(其中…).
4.对数的运算性质
如果,那么
加法:;
减法:;
数乘:;
;
;
四、对数函数及其性质
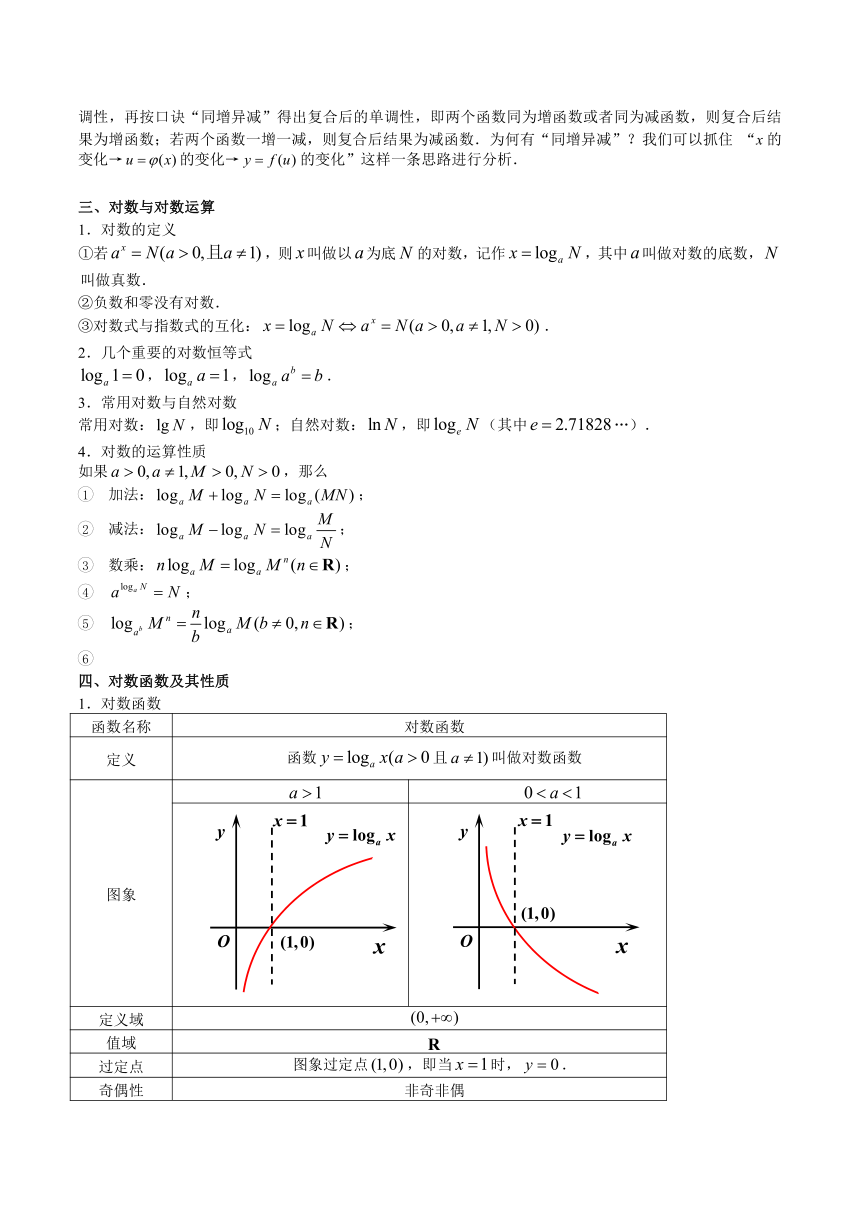
1.对数函数
函数名称
对数函数
定义
函数且叫做对数函数
图象
定义域
值域
过定点
图象过定点,即当时,.
奇偶性
非奇非偶
单调性
在上是增函数
在上是减函数
函数值的变化情况
变化对图象的影响
在第一象限内,越大图象越靠低;在第四象限内,越大图象越靠高.
2.反函数的概念
设函数的定义域为,值域为,从式子中解出,得式子.如果对于在中的任何一个值,通过式子,在中都有唯一确定的值和它对应,那么式子表示是的函数,函数叫做函数的反函数,记作,习惯上改写成.
反函数的求法:
①确定反函数的定义域,即原函数的值域;
②从原函数式中反解出;
③将改写成,并注明反函数的定义域.
例1
比较大小:(1),,;
(2),,.
解:(1)∵
在上是减函数,且,
∴
.
又
,所以.
(2)由
,得.
又,,
所以.
例2求下列函数的定义域:(1);(2).
解:(1)由,得,解得.
所以原函数的定义域为.
(2)由,即,
所以,解得.
所以,原函数的定义域为.
例3已知函数的区间上总有,求实数a的取值范围.
解:∵
,
∴
当时,,即.
∵
,
∴
,
解得.
当时,,即.
∵
,
∴
,
解得.
综上可得,实数a的取值范围是.
点评:先对底数a分两种情况讨论,再利用函数的单调性及已知条件,列出关于参数a的不等式组,解不等式(组)而得到参数的范围.解决此类问题的关键是合理转化与分类讨论.
例4讨论函数的单调性.
解:先求定义域,由,
解得.
设,易知为减函数.
又∵
函数是减函数,故函数在上单调递增.
例5
比较、、的大小.
解:在同一坐标系中分别画出的图象,分别作出当自变量x取3,0.4,0.3时的函数值.
观察图象容易得到:.
五、幂函数
1.幂函数的定义
一般地,函数叫做幂函数,其中为自变量,是常数.
2.幂函数的图象
3.幂函数的性质
①图象分布:幂函数图象分布在第一、二、三象限,第四象限无图象.幂函数是偶函数时,图象分布在第一、二象限(图象关于轴对称);是奇函数时,图象分布在第一、三象限(图象关于原点对称);是非奇非偶函数时,图象只分布在第一象限.
②过定点:所有的幂函数在都有定义,并且图象都通过点.
③单调性:如果,则幂函数的图象过原点,并且在上为增函数.如果,则幂函数的图象在上为减函数,在第一象限内,图象无限接近轴与轴.
④奇偶性:当为奇数时,幂函数为奇函数,当为偶数时,幂函数为偶函数.当(其中互质,和),若为奇数为奇数时,则是奇函数,若为奇数为偶数时,则是偶函数,若为偶数为奇数时,则是非奇非偶函数.
⑤图象特征:幂函数,当时,若,其图象在直线下方,若,其图象在直线上方,当时,若,其图象在直线上方,若,其图象在直线下方.
例1已知幂函数与的图象与、轴都没有公共点,且的图象关于y轴对称,求的值.
解:∵
幂函数图象与、轴都没有公共点,∴
,解得.
又
∵
的图象关于y轴对称,
∴
为偶数,即得.
例2幂函数与在第一象限内的图象如图所示,则(
).
A.
B.
C.
D.
答案:C
解:由幂函数图象在第一象限内的分布规律,观察第一象限内直线的右侧,图象由下至上,依次是,,,,,所以有.选B.
点评:观察第一象限内直线的右侧,结合所记忆的分布规律.
注意比较两个隐含的图象与.
本章整合:
0
1
0
1
0
1
0
1
基
本
初
等
函
数
(Ⅰ)
指
数
与
指
数
函
数
指
数
根式
分数指数幂
无理数指数幂
运算性质
指
数
函
数
定义
图象:
“一撇或一捺”,
过点(0,1).
性质:
位于x轴上方,以x轴为渐近线
对数与对数函数
对
数
定义:
运算性质
对
数
函
数
定义:
图象:位于y轴右侧,以y轴为渐近线.
性质:过点(1,0)
幂函数
定义
具体的五
个幂函数
特征:过点(1,1),当时在上递增;当时,在上递减。
换底公式:
图象
基本初等函数(Ⅰ)
一、指数与指数幂的运算
1.根式的概念
①如果,且,那么叫做的次方根.当是奇数时,的次方根用符号表示;当是偶数时,正数的正的次方根用符号表示,负的次方根用符号表示;0的次方根是0;负数没有次方根.
②式子叫做根式,这里叫做根指数,叫做被开方数.当为奇数时,为任意实数;当为偶数时,.
③根式的性质:;当为奇数时,;当为偶数时,
.
2.分数指数幂的概念
①正数的正分数指数幂的意义是:且.0的正分数指数幂等于0.
②正数的负分数指数幂的意义是:且.0的负分数指数幂没有意义.注意口诀:底数取倒数,指数取相反数.
3.指数幂的运算性质
①
②
③
例1
化简:(1);
(2)(a>0,b>0);
(3).
解:(1)原式=.
(2)原式====.
(3)原式=.
点评:根式化分数指数幂时,切记不能混淆,注意将根指数化为分母,幂指数化为分子,根号的嵌套,化为幂的幂.正确转化和运用幂的运算性质,是复杂根式化简的关键.
例2
化简与求值:
(1);
(2).
解:(1)原式=
=
==4.
(2)原式=
==.
点评:形如的双重根式,当是一个平方数时,则能通过配方法去掉双重根号,这也是双重根号能否开方的判别技巧.
而分母有理化中,常常用到的是平方差公式,第(2)小题也体现了一种消去法的思想.
第(1)小题还可用平方法,即先算得原式的平方,再开方而得.
二、指数函数及其性质
1.指数函数
函数名称
指数函数
定义
函数且叫做指数函数
图象
定义域
值域
过定点
图象过定点,即当时,.
奇偶性
非奇非偶
单调性
在上是增函数
在上是减函数
函数值的变化情况
变化对图象的影响
在第一象限内,越大图象越高;在第二象限内,越大图象越低.
例1
求下列函数的定义域:
(1);
(2);
(3).
解:(1)要使有意义,其中自变量x需满足,即,∴
其定义域为.
(2)要使有意义,其中自变量x需满足,即,∴
其定义域为.
(3)要使有意义,其中自变量x需满足,即,∴其定义域为.
例2
求下列函数的值域:
(1);
(2).
解:(1)观察易知,
则有.
∴
原函数的值域为.
(2).
令,易知.
则.
结合二次函数的图象,由其对称轴观察得到在上为增函数,
所以.
∴
原函数的值域为.
例3
函数的图象如图,其中a、b为常数,则下列结论正确的是(
).
A.
B.
C.
D.
解:从曲线的变化趋势,可以得到函数为减函数,从而0<a<1;从曲线位置看,是由函数的图象向左平移|-b|个单位而得,所以-b>0,即b<0.
所以选D.
点评:观察图象变化趋势,得到函数的单调性,结合指数函数的单调性,得到参数a的范围.
根据所给函数式的平移变换规律,得到参数b的范围.
也可以取x=1时的特殊点,得到,从而b<0.
例4
已知.
(1)讨论的奇偶性;
(2)讨论的单调性.
解:(1)的定义域为R.
∵
.
∴
为奇函数.
(2)设任意,且,则
.
由于,从而,即.
∴
,即,
∴
为增函数.
点评:在这里,奇偶性与单调性的判别,都是直接利用知识的定义来解决.需要我们理解两个定义,掌握其运用的基本模式,并能熟练的进行代数变形,得到理想中的结果.
例5
求下列函数的单调区间:(1);
(2).
解:(1)设.
由知,在上为减函数,在上为增函数.
根据的单调性,当时,y关于u为增函数;当时,y关于u为减函数.
∴
当时,原函数的增区间为,减区间为;
当时,原函数的增区间为,减区间为.
(2)函数的定义域为.
设.
易知为减函数.
而根据的图象可以得到,在区间与上,y关于u均为减函数.
∴在上,原函数为增函数;在上,原函数也为增函数.
点评:研究形如的函数的单调性,可以有如下结论:当时,函数的单调性与的单调性相同;当时,函数的单调性与的单调性相反.
而对于形如的函数单调性的研究,也需结合的单调性及的单调性进行研究.
复合函数的单调性研究,遵循一般步骤和结论,即:分别求出与两个函数的单调性,再按口诀“同增异减”得出复合后的单调性,即两个函数同为增函数或者同为减函数,则复合后结果为增函数;若两个函数一增一减,则复合后结果为减函数.为何有“同增异减”?我们可以抓住
“x的变化→的变化→的变化”这样一条思路进行分析.
三、对数与对数运算
1.对数的定义
①若,则叫做以为底的对数,记作,其中叫做对数的底数,叫做真数.
②负数和零没有对数.
③对数式与指数式的互化:.
2.几个重要的对数恒等式
,,.
3.常用对数与自然对数
常用对数:,即;自然对数:,即(其中…).
4.对数的运算性质
如果,那么
加法:;
减法:;
数乘:;
;
;
四、对数函数及其性质
1.对数函数
函数名称
对数函数
定义
函数且叫做对数函数
图象
定义域
值域
过定点
图象过定点,即当时,.
奇偶性
非奇非偶
单调性
在上是增函数
在上是减函数
函数值的变化情况
变化对图象的影响
在第一象限内,越大图象越靠低;在第四象限内,越大图象越靠高.
2.反函数的概念
设函数的定义域为,值域为,从式子中解出,得式子.如果对于在中的任何一个值,通过式子,在中都有唯一确定的值和它对应,那么式子表示是的函数,函数叫做函数的反函数,记作,习惯上改写成.
反函数的求法:
①确定反函数的定义域,即原函数的值域;
②从原函数式中反解出;
③将改写成,并注明反函数的定义域.
例1
比较大小:(1),,;
(2),,.
解:(1)∵
在上是减函数,且,
∴
.
又
,所以.
(2)由
,得.
又,,
所以.
例2求下列函数的定义域:(1);(2).
解:(1)由,得,解得.
所以原函数的定义域为.
(2)由,即,
所以,解得.
所以,原函数的定义域为.
例3已知函数的区间上总有,求实数a的取值范围.
解:∵
,
∴
当时,,即.
∵
,
∴
,
解得.
当时,,即.
∵
,
∴
,
解得.
综上可得,实数a的取值范围是.
点评:先对底数a分两种情况讨论,再利用函数的单调性及已知条件,列出关于参数a的不等式组,解不等式(组)而得到参数的范围.解决此类问题的关键是合理转化与分类讨论.
例4讨论函数的单调性.
解:先求定义域,由,
解得.
设,易知为减函数.
又∵
函数是减函数,故函数在上单调递增.
例5
比较、、的大小.
解:在同一坐标系中分别画出的图象,分别作出当自变量x取3,0.4,0.3时的函数值.
观察图象容易得到:.
五、幂函数
1.幂函数的定义
一般地,函数叫做幂函数,其中为自变量,是常数.
2.幂函数的图象
3.幂函数的性质
①图象分布:幂函数图象分布在第一、二、三象限,第四象限无图象.幂函数是偶函数时,图象分布在第一、二象限(图象关于轴对称);是奇函数时,图象分布在第一、三象限(图象关于原点对称);是非奇非偶函数时,图象只分布在第一象限.
②过定点:所有的幂函数在都有定义,并且图象都通过点.
③单调性:如果,则幂函数的图象过原点,并且在上为增函数.如果,则幂函数的图象在上为减函数,在第一象限内,图象无限接近轴与轴.
④奇偶性:当为奇数时,幂函数为奇函数,当为偶数时,幂函数为偶函数.当(其中互质,和),若为奇数为奇数时,则是奇函数,若为奇数为偶数时,则是偶函数,若为偶数为奇数时,则是非奇非偶函数.
⑤图象特征:幂函数,当时,若,其图象在直线下方,若,其图象在直线上方,当时,若,其图象在直线上方,若,其图象在直线下方.
例1已知幂函数与的图象与、轴都没有公共点,且的图象关于y轴对称,求的值.
解:∵
幂函数图象与、轴都没有公共点,∴
,解得.
又
∵
的图象关于y轴对称,
∴
为偶数,即得.
例2幂函数与在第一象限内的图象如图所示,则(
).
A.
B.
C.
D.
答案:C
解:由幂函数图象在第一象限内的分布规律,观察第一象限内直线的右侧,图象由下至上,依次是,,,,,所以有.选B.
点评:观察第一象限内直线的右侧,结合所记忆的分布规律.
注意比较两个隐含的图象与.
本章整合:
0
1
0
1
0
1
0
1
基
本
初
等
函
数
(Ⅰ)
指
数
与
指
数
函
数
指
数
根式
分数指数幂
无理数指数幂
运算性质
指
数
函
数
定义
图象:
“一撇或一捺”,
过点(0,1).
性质:
位于x轴上方,以x轴为渐近线
对数与对数函数
对
数
定义:
运算性质
对
数
函
数
定义:
图象:位于y轴右侧,以y轴为渐近线.
性质:过点(1,0)
幂函数
定义
具体的五
个幂函数
特征:过点(1,1),当时在上递增;当时,在上递减。
换底公式:
图象
