1.4力矩的平衡条件 课件 (1)36张PPT
文档属性
| 名称 | 1.4力矩的平衡条件 课件 (1)36张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 269.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2017-01-04 00:00:00 | ||
图片预览






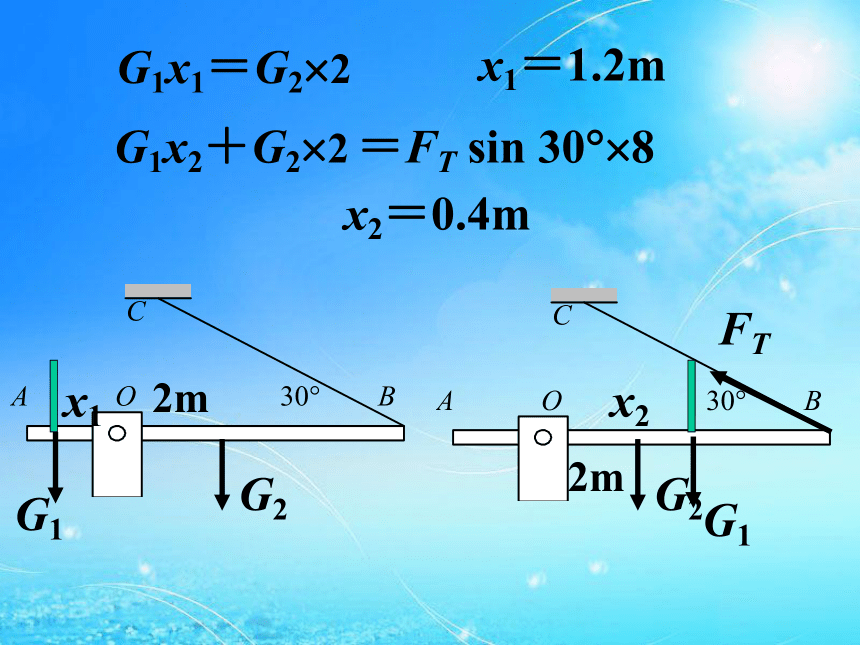
文档简介
课件36张PPT。力矩的平衡条件(2)最大可能值为力的作用点到转动轴的距离。一.力矩:M=FL1.力臂:(1)转动轴到力的作用线的垂直距离,练习:如图所示,直杆OA可绕O点转动,图中虚线与杆平行,杆端A点受四个力F1、F2、F3、F4的作用,力的作用线与OA杆在同一竖直平面内,它们对转轴O的力矩分别为M1、M2、M3、M4,则它们力矩间的大小关系是( )
(A)M1=M2>M3=M4,
(B)M2>M1=M3>M4,
(C)M4>M2>M3>M1,
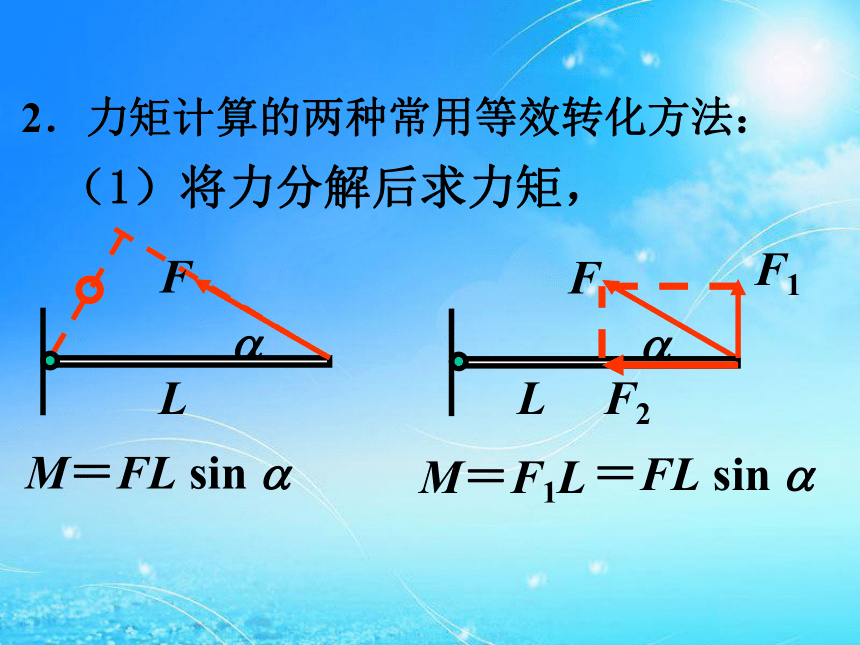
(D)M2>M1>M3>M4。(1)将力分解后求力矩, LM=FL sin ?M=F1L=FL sin ?2.力矩计算的两种常用等效转化方法: 练习:如图所示,直杆OA可绕O点转动,图中虚线与杆平行,杆端A点受四个力F1、F2、F3、F4的作用,力的作用线与OA杆在同一竖直平面内,它们对转轴O的力矩分别为M1、M2、M3、M4,则它们力矩间的大小关系是( )
(A)M1=M2>M3=M4,
(B)M2>M1=M3>M4,
(C)M4>M2>M3>M1,
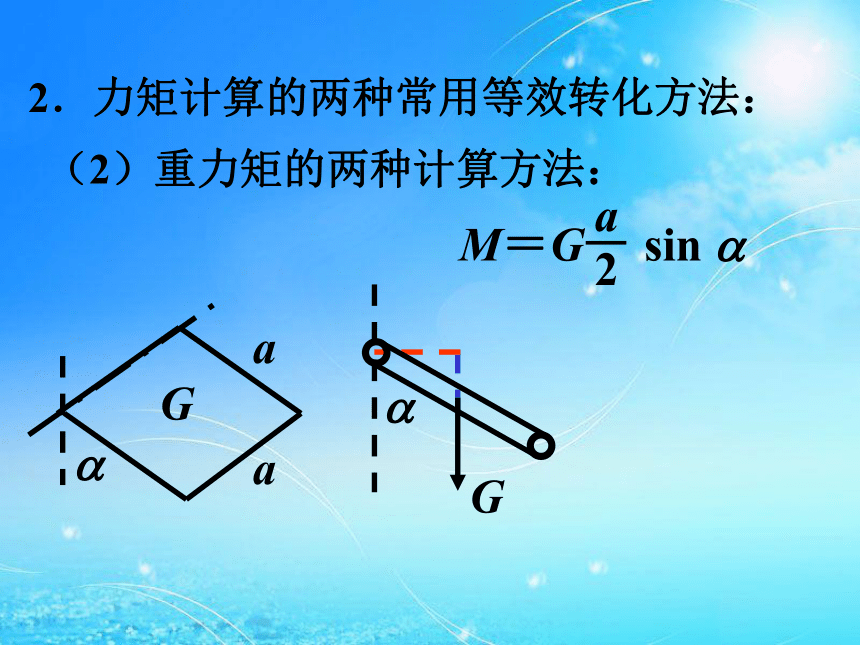
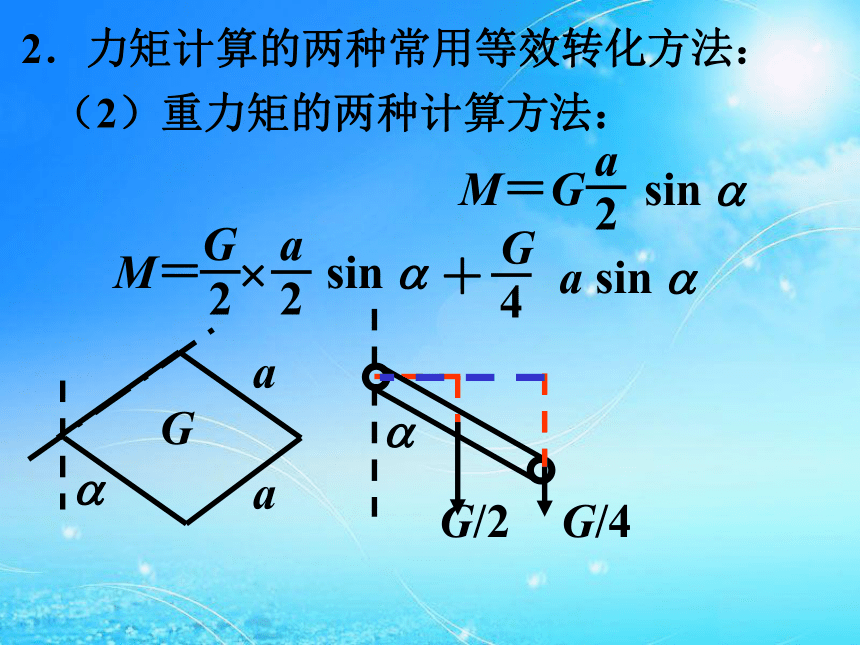
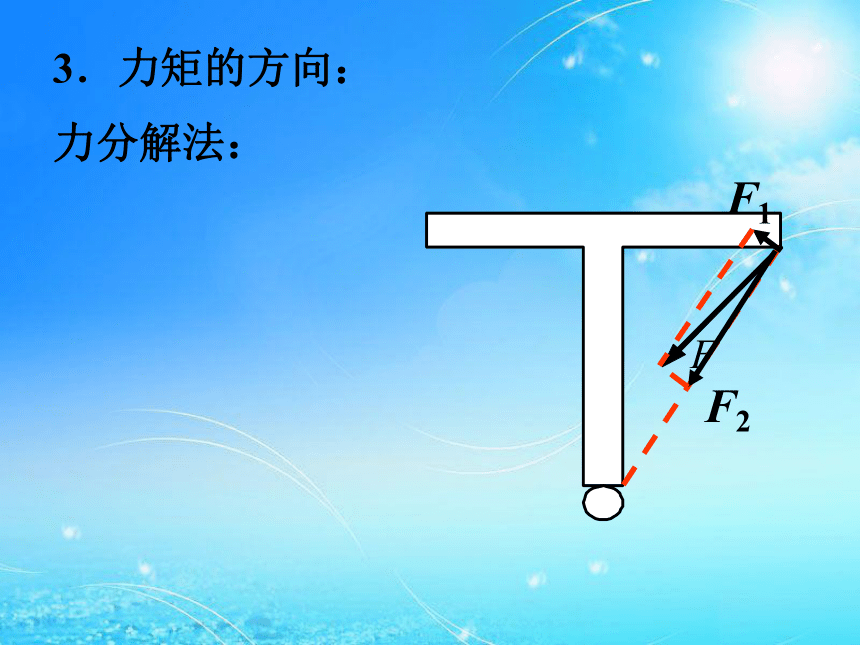
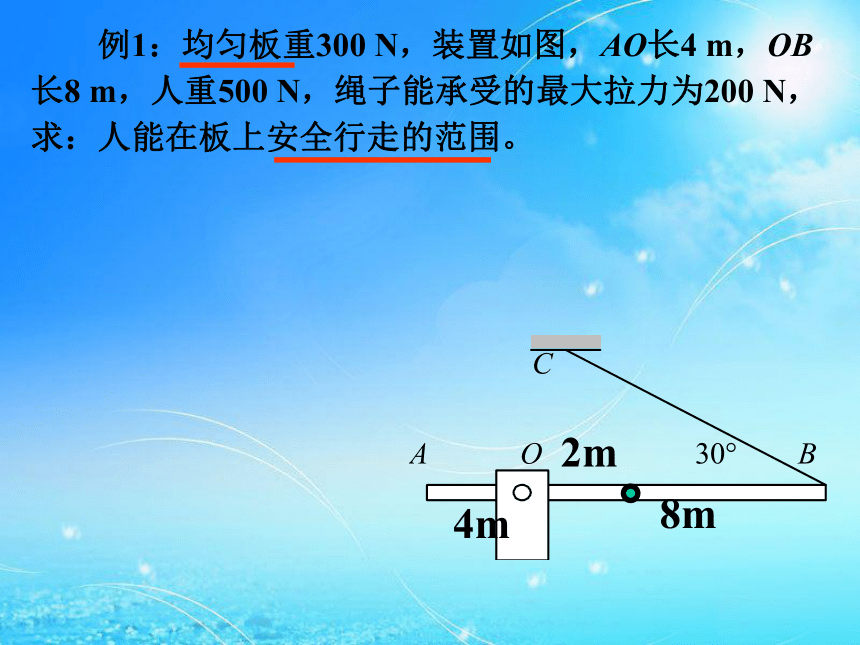
(D)M2>M1>M3>M4。(2)重力矩的两种计算方法: 2.力矩计算的两种常用等效转化方法: (2)重力矩的两种计算方法: G2.力矩计算的两种常用等效转化方法: 力分解法: 3.力矩的方向:M顺=M逆二.平衡与平衡条件:1.平衡状态:静止或匀速转动。 2.平衡条件:合外力矩为零。(1)选取研究对象,解题步骤:三.力矩平衡条件的应用:(2)受力分析(转动轴上的受力不用分析),(3)确定力臂、力矩方向,(4)列方程解方程。 例1:均匀板重300 N,装置如图,AO长4 m,OB长8 m,人重500 N,绳子能承受的最大拉力为200 N,求:人能在板上安全行走的范围。8m4m2mx12mG1x1=G2?22mx2G1x2+G2?2 =FT sin 30??8x1=1.2mx2=0.4m例2:一杆秤如图,杆及钩的总重为G,秤砣重为P,已知秤钩与杆的重心到提纽的距离OA和OG,求:(1)零刻度的位置,(2)证明刻度是均匀的,(3)讨论若秤砣换成2P,某刻度的读数是否为原来的两倍? AOGCAOGCBAOGC’AOGC’B’C’比C点更左些C’B’为CB的一半AOGBC’比C点更左些C’B’为CB的一半1.如左图匀质直角尺重为2G,C端为水平轴,不计摩擦,当BC部分处于水平静止时,试求加在A端的最小作用力。2.均匀杆,每米长重30 N,支于杆的左端,在离左端0.2 m处挂一重为300 N的重物,在杆的右端加一竖直向上的拉力F,杆多长时使杆平衡所需加的拉力F最小,此最小值为多大?Fx=G1x/2+G2l=?x2/2+G2lF=15x+60/x,因为15x?60/x为常数所以15x=60/x时F有最小值。即x=2m时Fmin=60N。3.如图,重为G、边长为a的均匀正方形板与长为2a的轻杆相连,支于轻杆中点,在杆的右端施一竖直向下的力F,使杆水平,求力F的大小,若为使杆与水平方向成30?角,力F又应多大?G(1.5a=Fa cos 30? ,0.5acos 30?-sin30?)解法一:Gcos 30??1.5a=Fa cos 30? 0.5a+G sin30??解法二:例4:有四根相同的刚性长薄片A、B、C、D,质量均为m,相互交叉成井字形,接触点均在各薄片的中点,放置在一只水平的碗口边(俯视图如图所示),并在D薄片右端的N点放上质量也为m的小物体,那么D薄片中点受到的压力为_____________。 FNB?2L=FNA?L+mg?L2FNB=FNA+mgFNB?2L=FNA?L+mg?L2FNB=FNA+mg2FNC=FNB+mg2FND=FNC+mgFNA?2L=mg?2L+FND?L+mg?L2FNB=FNA+mg2FNC=FNB+mg16FND=8FNC+8mgFNA?2L=mg?2L+FND?L+mg?L2FNA=FND+3mg4FNB=2FNA+2mg8FNC=4FNB+4mg2FND=FNC+mg2FNA=FND+3mgFND=17mg/1515FND=17mg例:如图所示,一根均匀直棒AB,A端用光滑铰链固定于顶板上,B端搁在一块表面粗糙的水平板上,现设板向上运动而棒AB匀速转动,则木板对棒的弹力说法正确的是 ( )
(A)逐渐变大, (B)先变大后变小,
(C)先变小后变大, (D)逐渐变小。GLG +?FNLf =FNLN四.动态平衡:练习1:一均匀的直角三直形木板ABC,可绕过C点的水平轴转动,如右图所示。现用一始终沿直角边AB且作用在A点的力F,使BC边慢慢地由水平位置转至竖直位置。在此过程中,力F的大小与α角变化的图线是( )FLF=GLGFLF=GLGFL=Ga cos(?+?)?练习1:一均匀的直角三直形木板ABC,可绕过C点的水平轴转动,如右图所示。现用一始终沿直角边AB且作用在A点的力F,使BC边慢慢地由水平位置转至竖直位置。在此过程中,力F的大小与α角变化的图线是( )2.如图所示,一根不均匀的铁棒AB与一辆拖车相连接,连接端B为一固定水平转动轴,拖车在水平面上做匀速直线运动,棒长为L,棒的质量为40kg,它与地面间的动摩擦因数为 3/3,棒的重心C距转动轴为2L/3,棒与水平面成30?角。运动过程中地面对铁棒的支持力为_______N;若将铁棒B端的固定转动轴向下移一些,其他条件不变,则运动过程中地面对铁棒的支持力将比原来__________(选填“增大”、“不变”或“减小”)。 FNL cos?+?FNL sin?=200 NFN=2mg/(1+? tan?)3.如图所示,质量为m粗细均匀的均质细杆AB在B点用铰链与墙连接,杆与竖直墙面的夹角为?=37?,A端固定一轻质光滑小滑轮,墙上C点固定轻绳的一端,轻绳水平跨过滑轮另一端悬挂有质量为M的物体G。目前杆AB与物体G都处于静止状态,则杆的质量与物体的质量的比值为m:M=________;若略微增加物体G的质量,仍要使整个系统处于平衡状态,可适当________(选填“增大”或“减小”)θ角的大小。(sin37?=0.6,cos37?=0.8)MgLsin?+mgLsin? /2 =MgLcos?2M(cos?-sin?)=msin? m:M=2:3 G增大时,逆时针力矩增加的多3.如图所示,质量为m粗细均匀的均质细杆AB在B点用铰链与墙连接,杆与竖直墙面的夹角为?=37?,A端固定一轻质光滑小滑轮,墙上C点固定轻绳的一端,轻绳水平跨过滑轮另一端悬挂有质量为M的物体G。目前杆AB与物体G都处于静止状态,则杆的质量与物体的质量的比值为m:M=________;若略微增加物体G的质量,仍要使整个系统处于平衡状态,可适当________(选填“增大”或“减小”)θ角的大小。(sin37?=0.6,cos37?=0.8)要再平衡必须增大顺时针力矩的力臂而减小逆时针力矩的力臂增大1.如图所示,长均为L,质量均为m的两根均匀直杆A、B,它们的上端用光滑铰链铰接,悬挂于天花板上,在距离两杆下端点均为L/3处,用光滑铰链M、N与轻弯杆C铰接,A、B两杆被弯杆C撑开的角度为2?,则可知弯杆C对杆A的作用力的方向为__________,大小为F=___________。2.如图所示,水平横梁的一端A插在墙壁内,另一端有光滑小滑轮B,一轻绳的一端C固定在墙壁上,另一端跨过滑轮后悬挂一质量为10 kg的重物,绳BC与梁成30?角,求滑轮受到绳子的作用力。F=G
(A)M1=M2>M3=M4,
(B)M2>M1=M3>M4,
(C)M4>M2>M3>M1,
(D)M2>M1>M3>M4。(1)将力分解后求力矩, LM=FL sin ?M=F1L=FL sin ?2.力矩计算的两种常用等效转化方法: 练习:如图所示,直杆OA可绕O点转动,图中虚线与杆平行,杆端A点受四个力F1、F2、F3、F4的作用,力的作用线与OA杆在同一竖直平面内,它们对转轴O的力矩分别为M1、M2、M3、M4,则它们力矩间的大小关系是( )
(A)M1=M2>M3=M4,
(B)M2>M1=M3>M4,
(C)M4>M2>M3>M1,
(D)M2>M1>M3>M4。(2)重力矩的两种计算方法: 2.力矩计算的两种常用等效转化方法: (2)重力矩的两种计算方法: G2.力矩计算的两种常用等效转化方法: 力分解法: 3.力矩的方向:M顺=M逆二.平衡与平衡条件:1.平衡状态:静止或匀速转动。 2.平衡条件:合外力矩为零。(1)选取研究对象,解题步骤:三.力矩平衡条件的应用:(2)受力分析(转动轴上的受力不用分析),(3)确定力臂、力矩方向,(4)列方程解方程。 例1:均匀板重300 N,装置如图,AO长4 m,OB长8 m,人重500 N,绳子能承受的最大拉力为200 N,求:人能在板上安全行走的范围。8m4m2mx12mG1x1=G2?22mx2G1x2+G2?2 =FT sin 30??8x1=1.2mx2=0.4m例2:一杆秤如图,杆及钩的总重为G,秤砣重为P,已知秤钩与杆的重心到提纽的距离OA和OG,求:(1)零刻度的位置,(2)证明刻度是均匀的,(3)讨论若秤砣换成2P,某刻度的读数是否为原来的两倍? AOGCAOGCBAOGC’AOGC’B’C’比C点更左些C’B’为CB的一半AOGBC’比C点更左些C’B’为CB的一半1.如左图匀质直角尺重为2G,C端为水平轴,不计摩擦,当BC部分处于水平静止时,试求加在A端的最小作用力。2.均匀杆,每米长重30 N,支于杆的左端,在离左端0.2 m处挂一重为300 N的重物,在杆的右端加一竖直向上的拉力F,杆多长时使杆平衡所需加的拉力F最小,此最小值为多大?Fx=G1x/2+G2l=?x2/2+G2lF=15x+60/x,因为15x?60/x为常数所以15x=60/x时F有最小值。即x=2m时Fmin=60N。3.如图,重为G、边长为a的均匀正方形板与长为2a的轻杆相连,支于轻杆中点,在杆的右端施一竖直向下的力F,使杆水平,求力F的大小,若为使杆与水平方向成30?角,力F又应多大?G(1.5a=Fa cos 30? ,0.5acos 30?-sin30?)解法一:Gcos 30??1.5a=Fa cos 30? 0.5a+G sin30??解法二:例4:有四根相同的刚性长薄片A、B、C、D,质量均为m,相互交叉成井字形,接触点均在各薄片的中点,放置在一只水平的碗口边(俯视图如图所示),并在D薄片右端的N点放上质量也为m的小物体,那么D薄片中点受到的压力为_____________。 FNB?2L=FNA?L+mg?L2FNB=FNA+mgFNB?2L=FNA?L+mg?L2FNB=FNA+mg2FNC=FNB+mg2FND=FNC+mgFNA?2L=mg?2L+FND?L+mg?L2FNB=FNA+mg2FNC=FNB+mg16FND=8FNC+8mgFNA?2L=mg?2L+FND?L+mg?L2FNA=FND+3mg4FNB=2FNA+2mg8FNC=4FNB+4mg2FND=FNC+mg2FNA=FND+3mgFND=17mg/1515FND=17mg例:如图所示,一根均匀直棒AB,A端用光滑铰链固定于顶板上,B端搁在一块表面粗糙的水平板上,现设板向上运动而棒AB匀速转动,则木板对棒的弹力说法正确的是 ( )
(A)逐渐变大, (B)先变大后变小,
(C)先变小后变大, (D)逐渐变小。GLG +?FNLf =FNLN四.动态平衡:练习1:一均匀的直角三直形木板ABC,可绕过C点的水平轴转动,如右图所示。现用一始终沿直角边AB且作用在A点的力F,使BC边慢慢地由水平位置转至竖直位置。在此过程中,力F的大小与α角变化的图线是( )FLF=GLGFLF=GLGFL=Ga cos(?+?)?练习1:一均匀的直角三直形木板ABC,可绕过C点的水平轴转动,如右图所示。现用一始终沿直角边AB且作用在A点的力F,使BC边慢慢地由水平位置转至竖直位置。在此过程中,力F的大小与α角变化的图线是( )2.如图所示,一根不均匀的铁棒AB与一辆拖车相连接,连接端B为一固定水平转动轴,拖车在水平面上做匀速直线运动,棒长为L,棒的质量为40kg,它与地面间的动摩擦因数为 3/3,棒的重心C距转动轴为2L/3,棒与水平面成30?角。运动过程中地面对铁棒的支持力为_______N;若将铁棒B端的固定转动轴向下移一些,其他条件不变,则运动过程中地面对铁棒的支持力将比原来__________(选填“增大”、“不变”或“减小”)。 FNL cos?+?FNL sin?=200 NFN=2mg/(1+? tan?)3.如图所示,质量为m粗细均匀的均质细杆AB在B点用铰链与墙连接,杆与竖直墙面的夹角为?=37?,A端固定一轻质光滑小滑轮,墙上C点固定轻绳的一端,轻绳水平跨过滑轮另一端悬挂有质量为M的物体G。目前杆AB与物体G都处于静止状态,则杆的质量与物体的质量的比值为m:M=________;若略微增加物体G的质量,仍要使整个系统处于平衡状态,可适当________(选填“增大”或“减小”)θ角的大小。(sin37?=0.6,cos37?=0.8)MgLsin?+mgLsin? /2 =MgLcos?2M(cos?-sin?)=msin? m:M=2:3 G增大时,逆时针力矩增加的多3.如图所示,质量为m粗细均匀的均质细杆AB在B点用铰链与墙连接,杆与竖直墙面的夹角为?=37?,A端固定一轻质光滑小滑轮,墙上C点固定轻绳的一端,轻绳水平跨过滑轮另一端悬挂有质量为M的物体G。目前杆AB与物体G都处于静止状态,则杆的质量与物体的质量的比值为m:M=________;若略微增加物体G的质量,仍要使整个系统处于平衡状态,可适当________(选填“增大”或“减小”)θ角的大小。(sin37?=0.6,cos37?=0.8)要再平衡必须增大顺时针力矩的力臂而减小逆时针力矩的力臂增大1.如图所示,长均为L,质量均为m的两根均匀直杆A、B,它们的上端用光滑铰链铰接,悬挂于天花板上,在距离两杆下端点均为L/3处,用光滑铰链M、N与轻弯杆C铰接,A、B两杆被弯杆C撑开的角度为2?,则可知弯杆C对杆A的作用力的方向为__________,大小为F=___________。2.如图所示,水平横梁的一端A插在墙壁内,另一端有光滑小滑轮B,一轻绳的一端C固定在墙壁上,另一端跨过滑轮后悬挂一质量为10 kg的重物,绳BC与梁成30?角,求滑轮受到绳子的作用力。F=G
