苏科版中考数学一轮复习知识点

初中知识点汇总
每次课前十分钟记忆、理解，上课抽查！
第一篇
代数
1、(1)有理数:
整数(包括：正整数、0、负整数)和分数(包括：有限小数和无限环循小数)都是有理数．如：－3， ，0.231，0.737373…， ， ．
(2)无理数:无限不环循小数叫做无理数． 如：π，－ ，sin60°，0.1010010001…(两个1之间依次多1个0)等．
(3)实数:有理数和无理数统称为实数．实数与数轴上的点一一对应。
2、 绝对值：a≥0 丨a丨＝a； a≤0 丨a丨＝－a．如：丨－ 丨＝ ；丨3.14－π丨＝π－3.14．
3、近似数，从左边笫一个不是0的数字起，到最末一个数字止，所有的数字，都叫做这个 近似数的有效数字．如：0.05972精确到0.001得0.060，结果有两个有效数字6，0；2.0×精确到十位，2.0
精确到十分位，有效数字都有两个2,0.
4、科学记数法:把一个数写成±a×10n 的形式(其中1≤a＜10，n是整数)，这种记数法叫做科学记数法．如：－40700＝－4.07×104，0.000043＝ 4.3×10－5．有效数学字往往和科学计数法结合起来考，（保留4个有效数字），（保留2个有效数字）
，（保留2个有效数字），（保留2个有效数字）
5、整式的乘除法：①几个单项式相乘除，系数与系数相乘除，同底数的幂结合起来相乘除． ②单项式乘以多项式，用单项式乘以多项式的每一个项．③多项式乘以多项式，用一个多 项式的每一项分别乘以另一个多项式的每一项．④多项式除以单项式，将多项式的每一项 分别除以这个单项式．（单项式、多项式的次数、系数）
一个单项式中，所有字母的指数的和叫做这个单项式的次数。如是6次单项式。例如：①的系数为，次数为5次；②的系数为，次数为3次。
幂的运算性质：① am×an＝am＋n．②am÷an＝am－n(a≠0)．③(am)n＝amn．④(ab)n＝anbn．⑤
a－n＝(a≠0)， ⑥ a0＝1(a≠0)．如：a3×a2＝a5，a6÷a2＝a4，(a3)2＝a6，(3a3 )3＝27a9，(－3)－1＝－ ，5－2＝ ＝ ，
( )－2＝( )2＝ ，(－3.14) ＝1， ( － )0＝1．
7、乘法公式(反过来就是因式分解的公式)：
①平方差公式
(a＋b)(a－b)＝a2－b2．符号相同的项的平方减去只有符号不同项的平方
（a-b-c)(a+b-c)=(a-c)2-b2=……
②完全平方公式
(a±b)2＝a2±2ab＋b2．各项平方和带上两两积2倍
8、选择因式分解方法是：先看能否提公因式．在没有公因式的情况下：二项式用平方 差公式a2－b2=(a＋b)(a－b)，三项式用十字相乘法(特殊的用完全平方公式a2±2ab＋b2=(a±b)2)，三项以上用分 组分解法．注意：因式分解要进行到每一个多项式因式都不能再分解为止．因式分解一定要注意最后结果是乘积的形式
9.分式:整式A除以整式B，可以表示成的形式，如果除式B中含有字母，那么称为分式．注：（1）若B≠0，则有意义；（2）若B=0，则无意义；（2）若A=0且B≠0，则=0
。对于化简求值的题型，代入的值要使分母有意义。
10、分式的运算：乘除法要先把分子、分母都分解因式，并颠倒除式，约分后相乘；加减法应 先把分母分解因式，再通分(不能去分母)．注意：结果要化为最简分式．
11、平方根：一般地，如果一个数x的平方等于a,即x2=a那么这个数a就叫做x的平方根（也叫做二次方根式）。一个正数有两个平方根，它们互为相反数；0只有一个平方根，它是0本身；负数没有平方根．
12．算术平方根：一般地，如果一个正数x的平方等于a,即x2=a，那么这个正数x就叫做a的算术平方根，0的算术平方根是0．
13.二次根式：（1）最简二次根式应满足的条件：（1）被开方数的因式是整式或整数；（2）被开方数中不含有能开得尽的因数或因式．如是最简二次根式，而则不是最简二次根式：几个二次根式化成最简二次根式以后，如果被开方数相同，这几个二次根式就叫做同类二次根式
如①与
②若最简二次根式
（3）.二次根式运算注意事项：（1）二次根式相加减，先把各根式化为最简二次根式，再合并同类二次根式，防止：①该化简的没化简；②不该合并的合并；③化简不正确；④合并出错．（2）二次根式的乘法除法常用乘法公式或除法公式来简化计算，运算结果一定写成最简二次根式或整式．
（4）二次根式化简：注意的运用
例如
⑴（x≥2）
易错点：平方根与算术平方根不分，如
64的平方根为士8，易丢掉－8；
，，
的算术平方根是2；的平方根是±2；
14．一元二次方程：
一．一元二次方程：只含有一个未知数，未知数的最高次数是2，且系数不为
0，这样的方程叫一元二次方程．
一般形式：ax2＋bx+c=0(a≠0）
一元二次方程ax2＋bx+c=0；ax2＋bx+c=0是一元二次方程；方程ax2＋bx+c=0有两个解均说明a≠0。
只说方程ax2＋bx+c=0可能一元一次方程也可能一元二次方程
二．一元二次方程的解法：
(1)直接开平方法
(2)
配方法：步骤是①化二次项系数为1，方程两边同除以二次项系数；②移项，使方程的左边为二次项和一次项，右边为常数项；③配方，即方程两边都加上一次项系数一半的平方；④化原方程为(x+m）2=n的形式；⑤如果n≥0就可以用两边开平方来求出方程的解；如果n＜0，则原方程无解．
公式法：公式法是用求根公式求出一元二次方程的解的方法．一元二次方程的求根公式是
(b2－4ac≥0)
(4)因式分解法：步骤是①将方程右边化为0；②将方程左边分解为两个一次因式的乘积③令每个因式等于0，得到两个一元一次方程，解这两个一元一次方程，它们的解就是原一元二次方程的解．
三．一元二次方程的注意事项：
⑴
在一元二次方程的一般形式中要注意，强调a≠0．因当a=0时，不含有二次项，即不是一元二次方程．如关于x的方程（k2－1）x2+2kx+1=0中，当k=±1时就是一元一次方程了．
⑵
应用求根公式解一元二次方程时应注意：①化方程为一元二次方程的一般形式；②确定a、b、c的值；③求出b2－4ac的值；④若b2－4ac≥0，则代人求根公式，求出x1
,x2．若b2－4ac＜0，则方程无解．
⑶
方程两边不能随便约去含有未知数的代数式．如－2(x＋4)2=3（x＋4）中，不能随便约去（x＋4），得-2（x+4）=3或x+4=0
⑷
注意解一元二次方程时一般不使用配方法（除特别要求外），x2-8x=…适合配方解，x2-7x=…不适合配方解，应用题中较大数据如x2-6x-7912=0适合配方解，配方方法很重要，对二次三项式的配方可求最值。应用题中增长率a(1±x)2=b直接开平方。解一元二次方程的一般顺序是：直接开平方法→因式分解法→公式法→配方法．
四.根的判别式为△＝
(注意a≠0)
五、根与系数的关系：
六、一元二次方程的应用：面积问题;
增长率a(1±x)2=b;
销售问题
15．分式方程：分母中含有未知数的方程叫做分式方程．解分式方程的步骤:①去分母,化为整式方程;②解整式方程;③验根;④下结论.因为解分式方程可能出现增根，所以解分式方程必须检验．分式方程无解是指①去分母后整式方程无解②使分式方程分母为零；分式方程有增跟是指①去分母后整式方程有解②使分式方程分母为零.
应用题中的分式方程检验的格式：经检验，是原方程的解且符合题意。
16．不等式：两边都乘以或除以同一个负数，不等号要改变方向．（等式的性质：两边同乘以或除以一个不为零的数，等式成立）
例⑴由
例⑵解不等式组
∴原不等式的解集为－4＜x≤
注：若又要求整数解，请务必注意看清要求，得整数解为－3，－2，－1，0
解应用题设、列、解、验（明验如分式方程，人数为负数；暗验是否符合题目中范围等）、答。最后一定要写答（一般1分）；
17．平面直角坐标系：①各限象内点的坐标如图所示．
②横轴(x轴)上的点，纵坐标是0；纵轴(y轴)上的点，横坐标是0．
③关于横轴对称的两个点，横坐标相同(纵坐标互为相反数)；
关于纵轴对称的两个点，纵坐标相同(横坐标互为相反数)；
关于原点对称的两个点，横坐标、纵坐标都互为相反数．
P（x，y）关于x轴对称P1（x，－y）(即x不变)；到x轴的距离为
P（x，y）关于y轴对称P2（－x，y）(即y不变)；
到y轴的距离为
P（x，y）关于原点对称P3（－x，－y）(即x，y都变)；
到原点的距离为
与坐标有关的常用公式
距离公式：
(解题中交代勾股定理即可)
直线l1:y＝k1x＋b1和
l2:y＝k2x＋b2
l1∥l2则k1
=k2且b1≠b2；l1⊥l2则k1
k2=
-1
直线l与x轴夹角（取锐角）则（直线过一、三象限k>0,
直线过二、四象限k<0）
（书中没有的定理大题慎用，小题直接用，实在没辙，用！）
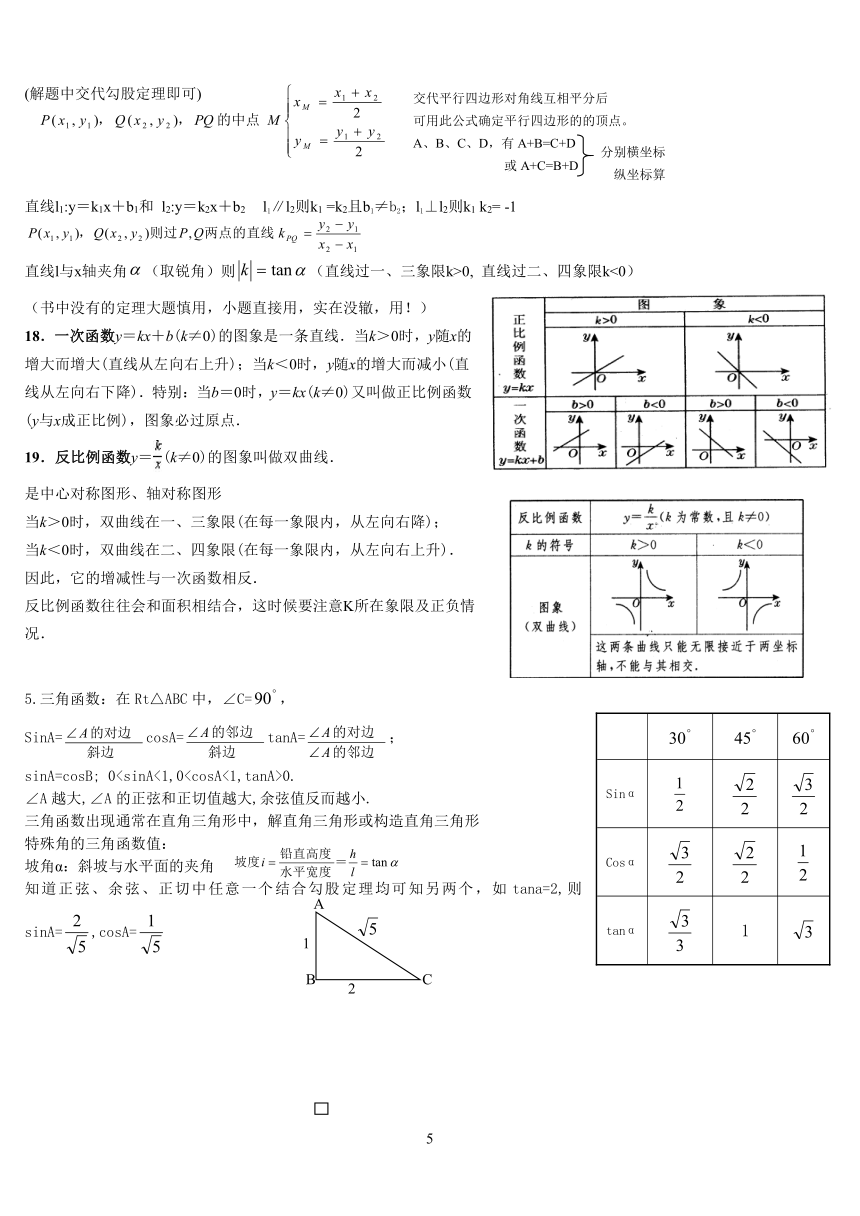
18．一次函数y＝kx＋b(k≠0)的图象是一条直线．当k＞0时，y 随x的增大而增大(直线从左向右上升)；当k＜0时，y随x的增大而减小(直线从左向右下降)．特别：当b＝0时，y＝kx (k≠0)又叫做正比例函数(y与x成正比例)，图象必过原点．
19．反比例函数y＝ (k≠0)的图象叫做双曲线．
是中心对称图形、轴对称图形
当k＞0时，双曲线在一、三象限(在每一象限内，从左向右降)；
当k＜0时，双曲线在二、四象限(在每一象限内，从左向右上升)．
因此，它的增减性与一次函数相反．
反比例函数往往会和面积相结合，这时候要注意K所在象限及正负情况．
Sinα
Cosα
tanα
1
5.三角函数：在Rt△ABC中，∠C=，
SinA=cosA=tanA=；
sinA=cosB;
00.
∠A越大,∠A的正弦和正切值越大,余弦值反而越小.
三角函数出现通常在直角三角形中，解直角三角形或构造直角三角形
特殊角的三角函数值：
坡角α：斜坡与水平面的夹角
知道正弦、余弦、正切中任意一个结合勾股定理均可知另两个，如tana=2,则sinA=,cosA=
20．二次函数
一.定义:一般形如y=ax2+bx+c(a、b、c常数且a≠0)的函数称为二次函数。
二.
图象函数y=ax2+bx+c
(a≠0)的图象是抛物线；
1.图象画法:(1)确定顶点,利用抛物线的对称性列表描点作图.(2)利用抛物线的顶点、与x轴、y轴交点等特殊点作图.
2.图象变化:(1)平移变化：a不变①一般式y=ax2+bx+c：左加右减上加下减②顶点式y＝a(x－h)2＋k顶点(h，k)变化(2)翻折变化:
关于x、y轴轴对称,关于谁谁不变(3)旋转变化:
①关于原点都改变；②关于顶点旋转180°，a变-a(顶点式)
3.图象性质
特别：抛物线顶点式y＝a(x－h)2＋k的顶点坐标是(h，k)，对称轴是：直线x＝h．
抛物线交点式与x轴交点为对称轴是：直线x=
三.
二次函数的图象与一元二次方程的根的关系:
四、二次函数解析式
⑴一般式：;
（2）顶点式：顶点为（h,k）可设y=a(x-h)+k;
（3）交点式：与x轴交点为
求解析式的设法 ①已知三个点的坐标，则设为一般形式y＝ax2＋bx＋c；②已知顶 点坐标
(h，k)，则设为顶点式y＝a(x－h)2＋k；③已知抛物线与x轴的两个交点坐标(x1，0)和(x2，0)， 则设为交点式y＝a(x－x1)(x－x2)，结果要化成一般式或顶点式
第二篇
空间与图形
一、角（10=60/,1/=60//)
角平分线的性质：角平分线平分角；角平分线上的点到角两边的距离相等。
角平分线的判定：定义；角的内部，到角两边距离相等的点在这个角的平分线上。
二、相交线与平行线
1.余角、补角、对顶角（相交）的性质：同角或等角的余角相等；同角或等角的补角相等；
对顶角相等。
2.垂直
(1)垂线的性质：①过一点有且只有一条直线与已知直线垂直；②直线外一点与直线上各点连结的所有线段中，垂线段最短；
（2）线段垂直平分线的性质：线段垂直平分线上的点到线段两端点的距离相等，
线段垂直平分线的判定：到线段两端点的距离相等的点在线段的垂直平分线上；
3.平行
两条平行线间的距离处处相等．
两个三角形面积相等
如：正方形ABCD、正方形BEFG和正方形RKPF的位置如图所示，
点G在线段DK上，正方形BEFG的边长为4，则△DEK的面积
为
连结DB、GE、FK，它们是一组平行线.
S△DEK=S△GED+
S△GEK=
S△GEB+
S△GEF=16
（1）平行线的性质
：①两直线平行，同位角相等；②两直线平行，内错角相等；③两直线平行，同旁内角互补
（2）平行线的判定：
①同位角相等，两直线平行；②内错角相等，两直线平行；③同旁内角互补，两直线平行；
（3）平行的性质：经过直线外一点有且只有一条直线平行于已知直线。
网格线中处理平行、垂直、旋转关系，注意旋转方向逆时针顺时针，旋转综合题可以考虑辅助圆，网格线中处理三角形，SSS勾股定理常用
三、三角形
1.三角形的有关性质：
①三角形的三边关系：三角形的两边之和大于第三边，两边之差小于第三边；
②三角形的内角和定理：三角形的三个内角的和等于；
③三角形的外角和定理：三角形的一个外角等于和它不相邻的两个内角的和；三角形的一个外角大于任何一个和它不相邻的内角
④三角形中位线定理：三角形两边中点的连线平行于第三边，并且等于第三边的一半；
2.全等三角形
（1）定义：两个能够重合的三角形是全等三角形。
（2）性质：全等三角形的对应边相等，对应角相等。
（3）三角形全等的条件：
边角边（SAS）；角边角（ASA）；角角边（AAS）；边边边（SSS）；斜边、直角边（HL）
3.等腰三角形
(1)等腰三角形的性质：①等腰三角形的两腰相等；等腰三角形的两个底角相等（等边对等角）
②等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合（三线合一）
(2)等腰三角形的判定：有两个角相等的三角形是等腰三角形（等角对等边）；
4.直角三角形
（1）直角三角形的性质：①直角三角形的两个锐角互为余角；②直角三角形斜边上的中线等于斜边的一半；③直角三角形的两直角边的平方和等于斜边的平方（勾股定理）；④直角三角形中角所对的直角边等于斜边的一半；
（2）直角三角形的判定：
①有两个角互余的三角形是直角三角形；
②如果三角形的三边长a、b
、c有下面关系，那么这个三角形是直角三角形（勾股定理的逆定理）。
三角形的周长和面积：
常见辅助线：角平分线到角两边的距离、倍长中线，中位线（取一边中点）三线合一，直角三角形斜边中线（分得两个等腰三角形），构造全等，做平行线等等
四.多边形
（1）多边形的内角和定理：n边形的内角和等于
（n≥3，n是正整数）；
（2）多边形的外角和定理：任意多边形的外角和等于360°
（3）多边形的对角线：
各顶点等分圆周 正n
边
形
各边相等，各角相等，且每个内角＝ 度，中心角＝外角＝ 度．（圆内接正多边形的有关公式）
七、尺规作图（基本作图、利用基本图形作三角形和圆）作一条线段等于已知线段，作一个角等于已知角；作已知角的平分线；作线段的垂直平分线；
八、(1)平行投影：太阳光线可以看成是平行光线，像这样的光线形成的投影称为平行投影．
(2)中心投影：光线可以看成是从一点发出的，像这样的光线形成的投影称为中心投影．
第三篇
图形与变换
一.图形的轴对称的性质
轴对称的基本性质：(1)成轴对称的两图形全等;(2)对称点所连的线段被对称轴垂直平分；
二.图形的平移
图形的平移有两个要素：一是图形平移的方向，二是图形平移的距离。抓住一个点（顶点）或左加右减上加下减，如：y=-2x2+4x-4向左平移2个单位再向下平移1个单位
①y=-2（x+2）2+4（x+2）-4-1进一步化简得
②y=-2x2+4x-4化为顶点式y=
-2（x-1）2-2得顶点（1，-2）向左平移2个单位再向下平移1个单位得（-1，-3）有y=
-2（x+1）2-3
三.图形的旋转
1.图形旋转的基本性质：对应点到旋转中心的距离相等;对应点与旋转中心连线所成的角相等；旋转前后的两个图形全等.
图形旋转可能与圆有关，等边三角形正方形常常旋转思想全等证明
2.中心对称图形:
在平面内，一个图形绕某个点旋转180度，如果旋转前后的图形互相重合，那么这个图形叫做中心对称图形，这个点叫做它的对称中心。中心对称图形上的每一对对应点所连成的线段都被对称中心平分。
①线段
②射线
③直线
④角
⑤平行线
⑥等腰三角形
⑦等边三角形
⑧平行四边形
⑨矩形
⑩菱形
⑾正方形
⑿等腰梯形
⒀圆中，轴对称图形有①②③④⑤⑥⑦⑨⑩⑾⑿⒀；
中心对称图形有①③⑤⑧⑨⑩⑾⒀
(注意正n边形的对称性)
五．四边形
1．平行四边形
（1）平行四边形的性质：平行四边形的两组对边分别平行；平行四边形的两组对边分别相等；平行四边形的两组对角分别相等；平行四边形的对角线互相平分．
（2）平行四边形的判定：两组对边分别平行的四边形是平行四边形．两组对边分别相等的四边形是平行四边形．一组对边平行且相等的四边形是平行四边形．对角线互相平分的四边形是平行四边形．
平行四边形相对的顶点的坐标之和相等；
已知三个点求第四个点，若顺序给定一解，若顺序未给定三解；
已知一边（线段）求点，分两种情况讨论：边和对角线
2.矩形
(1)矩形的性质：（除具有平行四边形所有性质外）①矩形的四个角都是直角；②矩形的对角线相等；
(2)矩形的判定：①有三个角是直角的四边形是矩形；②对角线相等的平行四边形是矩形；③有一个角是直角的平行四边形叫做矩形.
3.菱形
(1)菱形的性质：（除具有平行四边形所有性质外）①菱形的四边相等；②菱形的对角线互相垂直平分，并且每一条对角线平分一组对角；
(2)菱形的判定：①四边相等的四边形是菱形；②对角线互相垂直的平行四边形是菱形.③有一组邻边相等的平行四边形叫做菱形
4.正方形
(1)正方形的性质：①正方形的四边相等；②正方形的四个角都是直角；③正方形的两条对角线相等，且互相垂直平分，每一条对角线平分一组对角；
(2)正方形的判定：①有一个角是直角的菱形是正方形；②有一组邻边相等的矩形是正方形。③有一组邻边相等且有一个角是直角的平行四边形叫做正方形
5.等腰梯形
(1)等腰梯形的性质:①等腰梯形同一底边上的两个底角相等②等腰梯形的两条对角线相等。
(2)等腰梯形的判定：①同一底边上的两个角相等的梯形是等腰梯形；②两条腰相等的梯形是等腰梯形。
,；；
；
六、圆
1.圆有关的概念:
圆的定义：到定点的距离等于定长的点的集合。定义用来判断几点共圆，也可画出辅助圆解决问题。
（1）圆心角：顶点在圆心的角叫做圆心角．
（2）圆周角：顶点在圆上，并且两边都和圆相交的角叫做圆周角．
（3）弧：圆上任意两点间的部分叫做圆弧，简称弧，大于半圆的弧称为优弧，小于半圆的弧称为劣弧．等弧是完全重合的弧，包括弧长和弧度（所对圆心角度数）,只能在同圆或等圆中。
（4）弦：连接圆上任意两点的线段叫做弦，经过圆心的弦叫做直径．
2.圆的有关的性质：
（1）圆心角、弦和弧三者之间的关系：在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量分别相等；
（2）垂径定理：垂直于弦的直径平分弦，并且平分弦所对的两条弧；
（3）圆心角定理：圆心角的度数等于它所对弧的度数；
（4）圆心角与圆周角的关系:
同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半．
（5）圆周角定理：直径所对的圆周角是直角，反过来，90°的圆周角所对的弦是直径；
（6）切线的判定：①经过半径的外端并且垂直于这条半径的直线是圆的切线；②圆心到直线的距离等于半径；③直线与圆只有唯一的公共点。
方法：(无切点)作垂直，证半径;(有切点)连半径，证垂直。
（7）切线的性质定理：圆的切线垂直于过切点的半径；
（8）切线长定理：从圆外一点引圆的两条切线，它们的切线长相等，这点与圆心的连线平分两切线的夹角；
圆中常作的辅助线：已知切线，常过切点作半径；已知直径，常作直径所对的圆周角；求解有关弦的问 题，作弦心距，借助垂径定理和勾股定理解决；弧的中点常和圆心连结。
圆中常作的解题思路：利用垂径定理勾股定理、相似三角形，同弧所对的圆周角相等，以及圆周角与圆心角之间的关系
若题目中只配有一幅图，有时不代表就只有一解。要注意题目中的条件：比如动点，直线等等字眼。油的截面问题是有图一解，无图两解；
3．三角形的内心和外心
(1)确定圆的条件：不在同一直线上的三个点确定一个圆．
(2)
1、
外心：三边中垂线的交点
2、
性质(1)OA=OB=OC.（2）外心不一定在三角形的内部．
3、
应用
∠BOC=2∠A
(3)
1、三角形的内心：三角形三条角平分线的交点
2、性质（1）到三边的距离相等；（2）IA、IB、IC分别平分∠BAC、∠ABC、∠ACB；
（3）内心在三角形内部．
3、应用∠BIC=900+∠A(三角形内角和角平分线得)；S⊿ABC=C⊿ABC
r内切
任意多边形的内切圆的半径与面积和周长公式之间的关系：S= CR ．
(4)直角三角形中
R外接=c
r内切=(a+b-c)
(5)等边三角形中边长为a
R外接=a，r内切=a,
h=a,
s=
4.点与圆的位置关系：点在圆外，点在圆上，点在圆内，设圆的半径为r，点到圆心的距离为d，则点在圆外d＞r．点在圆上d=r．点在圆内d＜r．
5．直线和圆的位置关系有三种：相交、相切、相离．
设圆的半径为r，圆心到直线的距离为d，则直线与圆相交d＜r，直线与圆相切d=r，直线与圆相离d＞r
6.圆与圆的位置关系:设两圆的圆心距为d，两圆的半径分别为R和r，则
⑴
两圆外离d＞R+r；
⑵
两圆外切d=R＋r；⑶
两圆相交R－r＜d＜R+r（R＞r）
⑷
两圆内切d=R－r（R＞r）⑸
两圆内含d＜R—r（R＞r）（R与r大小不定加绝对值）
判断两圆位置关系：圆心距、两圆半径和、两圆半径差（绝对值）
直线与圆是相离、相切、相交，圆与圆相离包含外离和内含，相切包括内切和外切
7.圆有关的计算:
(1)
(2)圆锥侧面展开图（扇形）1、h2+r2=l2
2、S
侧
=πRr
3、
l即为R,
圆锥母线长展开图扇形半径（大半径），r底面圆小半径
看清楚求的是扇形面积和弧长，面积是360作分母，弧长是180作分母；
概率与统计
一．统计
1.总体与样本:所要考察对象的全体叫做总体，其中每一个考察对象叫做个体，从总体中所抽取的一部分个体叫做总体的一个样本，样本中个体数目叫做样本容量。
如：为了了解我校九年级900名学生期中考试情况，从中抽取了100名学生的数学成绩进行统计，其中总体为我校九年级900名学生期中考试情况，样本为我校九年级100名学生期中考试的数学成绩，样本容量为100
2.众数与中位数
①众数：在一组数据中,出现次数最多的数(有时不止一个),叫做这组数据的众数.
②中位数：将一组数据按大小顺序排列,把处在最中间的一个数(或两个数的平均数)叫做这组数据的中位数.
3.平均数（易受极端数值的影响）
公式①
n个数、……,
的平均数为：；
②
如果在n个数中，出现次、出现次……,
出现次，并且+……+=n，则，这时也叫加权平均数，其中，，…，叫做权。
公司工资情况，老总关心平均数，工会主席关心众数，我关心中位数。
若一组数据的平均数为，方差为，标准差为;则，的平均数为，方差为,标准差为。
4.极差、方差与标准差计算公式：
(1)极差：极差=最大值-最小值；
(2)方差：=
(3)标准差：=
一组数据的方差越大,这组数据的波动就越大;一组数据的方差越小,这组数据的波动就越小,也就越稳定.
二、概率
1事件分为确定事件与不确定事件.
确定事件包括不可能事件概率为0、必然事件概率为1;不确定事件即为随机事件A,02.概率一般包括两种，一种是可放回的概率，另一种是不可放回的概率，
3.①概率P=;②可以用概率估计物体的个数m=n×P;③常用列表、画树状图计算事件发生的概率④大量的重复实验时频率可视为事件发生概率的估计值。
4．频数：落在各个小组内的数据的个数，频率：每一小组的频数与数据总数（样本容量n）的比值叫做这一小组的频率（所有频率的和为1）
注：求方差、概率、频率不要求近似计算时，应用准确值填入。
例：x2－2x＋2＝0
因为△＜0
所以不存在
x1＋x2，x1·x2
解：由①得
－x＜4
∴x＞－4
由②得
2－2x≥3x
∴x≤
交代平行四边形对角线互相平分后
可用此公式确定平行四边形的的顶点。
A、B、C、D，有A+B=C+D
或A+C=B+D
或A+D=B+C
分别横坐标
纵坐标算
1
2
B
C
A
>0
E点有两个
以DC为直径的圆
与AB相交
=0
E点一个
以DC为直径的圆
与AB相切
<0
E点没有
以DC为直径的圆
与AB相离
a
●
△=
●
S正方形=a2=
b是对角线长
等腰直角三角形
k型相似△ADE∽△BEC
得y2-8y+2x=0
△
=64-8x
对角线垂直的四边形面积
等于对角线乘积一半.
梯形
常见
辅助线
梯形中的面积：