高中数学 必修2 第一章 空间几何体 复习+练习
文档属性
| 名称 | 高中数学 必修2 第一章 空间几何体 复习+练习 |  | |
| 格式 | zip | ||
| 文件大小 | 797.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-01-04 08:34:19 | ||
图片预览

文档简介
第1章 空间几何体
一、柱、锥、台、球的结构特征
知识要点:
结 构 特 征
结 构 特 征
图例
棱柱
(1)两底面相互平行,其余各面都是平行四边形;
(2)侧棱平行且相等.
圆柱
(1)两底面相互平行;
(2)侧面的母线平行于圆柱的轴;
(3)是以矩形的一边所在直线为旋转轴,其余三边旋转形成的曲面所围成的几何体.
棱锥
(1)底面是多边形,各侧面均是三角形;
(2)各侧面有一个公共顶点.
圆锥
(1)底面是圆;
(2)是以直角三角形的一条直角边所在的直线为旋转轴,其余两边旋转形成的曲面所围成的几何体.
棱台
(1)两底面相互平行;(2)是用一个平行于棱锥底面的平面去截棱锥,底面和截面之间的部分.
圆台
(1)两底面相互平行;
(2)是用一个平行于圆锥底面的平面去截圆锥,底面和截面之间的部分.
球
(1)球心到球面上各点的距离相等;(2)是以半圆的直径所在直线为旋转轴,半圆面旋转一周形成的几何体.
例1下列说法错误的是( ).
A.多面体至少有四个面 B.九棱柱有9条侧棱,9个侧面,侧面为平行四边形
C.长方体、正方体都是棱柱 D.三棱柱的侧面为三角形
答案:D
例2一个棱柱有10个顶点,所有的侧棱长的和为60 cm,则每条侧棱长为___________ cm.
答案:12
例3在本节我们学过的常见几何体中,如果用一个平面去截几何体,如果截面是三角形,那么这个几何体可能是___________.www.21-cn-jy.com
答案:棱锥、棱柱、棱台、圆锥
二、空间几何体的三视图
知识要点:
把光由一点向外散射形成的投影叫中心投影,中心投影的投影线交于一点;把在一束平行光线照射下的投影叫平行投影,平行投影的投影线是平行的.2·1·c·n·j·y
(1)定义:
正视图:光线从几何体的前面向后面正投影得到的投影图;
侧视图:光线从几何体的左面向右面正投影得到的投影图;
俯视图:光线从几何体的上面向下面正投影得到的投影图.
几何体的正视图、侧视图和俯视图统称为几何体的三视图.
(2)三视图中反映的长、宽、高的特点:“长对正”,“高平齐”,“宽相等”.
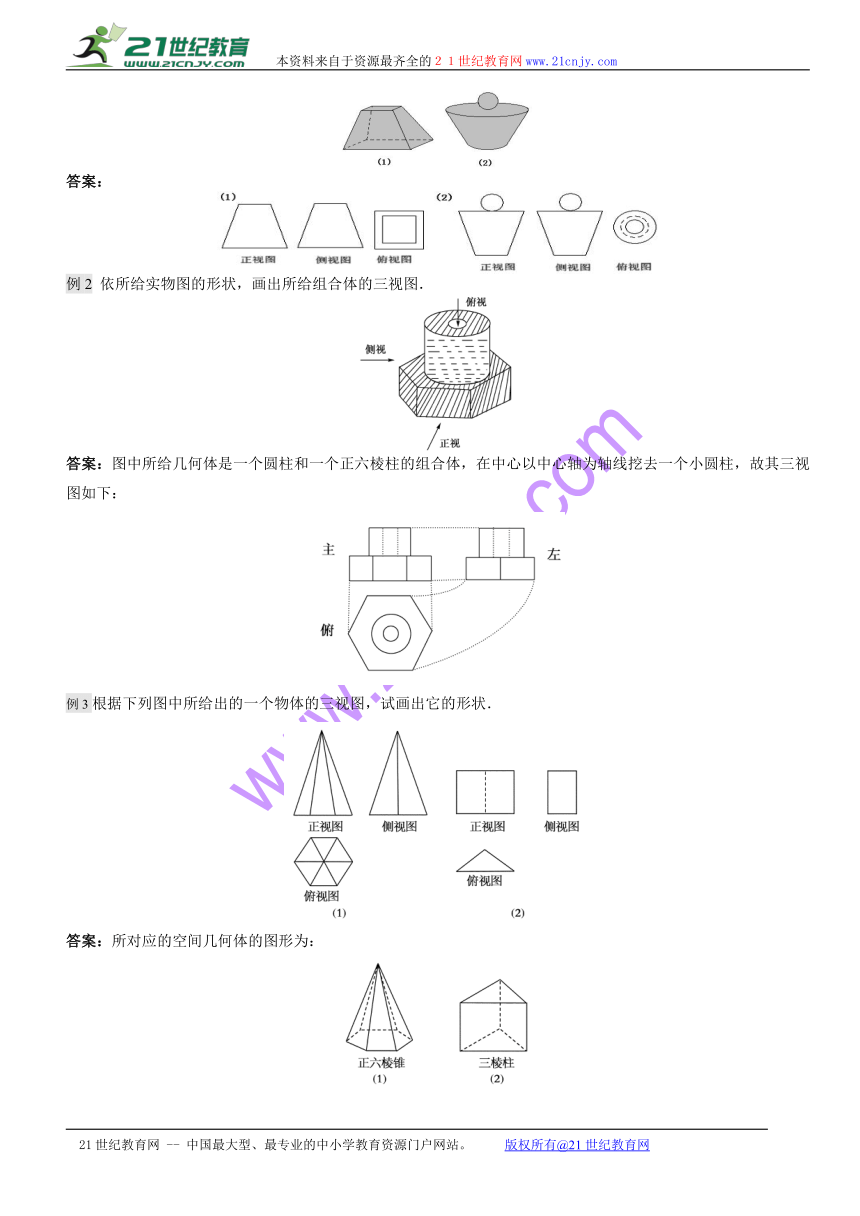
例1画出下列各几何体的三视图:
答案:
例2 依所给实物图的形状,画出所给组合体的三视图.
答案:图中所给几何体是一个圆柱和一个正六棱柱的组合体,在中心以中心轴为轴线挖去一个小圆柱,故其三视图如下:【来源:21·世纪·教育·网】
例3根据下列图中所给出的一个物体的三视图,试画出它的形状.
答案:所对应的空间几何体的图形为:
三、空间几何体的直观图
知识要点:
“直观图”最常用的画法是斜二测画法,由其规则能画出水平放置的直观图,其实质就是在坐标系中确定点的位置的画法, 基本步骤如下:21·世纪*教育网
(1)建系:在已知图形中取互相垂直的x轴和y轴,得到直角坐标系,直观图中画成斜坐标系,两轴夹角为.www-2-1-cnjy-com
(2)平行不变:已知图形中平行于x轴或y轴的线段,在直观图中分别画成平行于或轴的线段.
(3)长度规则:已知图形中平行于x轴的线段,在直观图中保持长度不变;平行于y轴的线段,长度为原来的一半.2-1-c-n-j-y
四、柱体、锥体、台体的表面积
知识要点:
表面积相关公式
表面积相关公式
棱柱
圆柱
(r:底面半径,h:高)
棱锥
圆锥
(r:底面半径,l:母线长)
棱台
圆台
(r:下底半径,:上底半径,l:母线长)
例1已知圆台的上下底面半径分别是2、5,且侧面面积等于两底面面积之和,求该圆台的母线长.
答案:
例2一个正三棱柱的三视图如右图所示,求这个正三棱柱的表面积.
答案:
五、柱体、锥体、台体的体积
知识要点:
体积公式:
体积公式
体积公式
棱柱
圆柱
棱锥
圆锥
棱台
圆台
柱、椎、台之间,可以看成一个台体进行变化,当台体的上底面逐渐收缩为一个点时,它就成了锥体;当台体的上底面逐渐扩展到与下底面全等时,它就成了柱体.因而体积会有以下的关系:21教育网
.
例1一个长方体的相交于一个顶点的三个面的面积分别是2、3、6,则长方体的体积是 .
答案:6
解析:设长方体的长宽高分别为,则,三式相乘得.所以长方体的体积为6.
例2一块边长为10的正方形铁片按如图所示的阴影部分裁下,然后用余下的四个全等的等腰三角形加工成一个正四棱锥形容器,试建立容器的容积V与x的函数关系式,并求出函数的定义域.21cnjy.com
解:如图,设所截等腰三角形的底边边长为.
在中,,所以,于是.依题意函数的定义域为.
例3一个无盖的圆柱形容器的底面半径为,母线长为6,现将该容器盛满水,然后平稳缓慢地将容器倾斜让水流出,当容器中的水是原来的时,圆柱的母线与水平面所成的角的大小为 .21·cn·jy·com
答案:
解析:容器中水的体积为.流出水的体积为,如图,.设圆柱的母线与水平面所成的角为α,则,解得.
六、球的体积和表面积
知识要点:
表面积: 体积:(R:球的半径).
例1设A、B、C、D是球面上的四个点,且在同一平面内,AB=BC=CD=DA=3,
球心到该平面的距离是球半径的一半,则球的体积是( ).
A. B. C. D.
答案:A
解析:由已知可得,A、B、C、D在球的一个小圆上.∵AB=BC=CD=DA=3,∴四边形为正方形,∴小圆半径.由得,解得.∴球的体积.所以选A.21世纪教育网版权所有
本章总结:
一、柱、锥、台、球的结构特征
知识要点:
结 构 特 征
结 构 特 征
图例
棱柱
(1)两底面相互平行,其余各面都是平行四边形;
(2)侧棱平行且相等.
圆柱
(1)两底面相互平行;
(2)侧面的母线平行于圆柱的轴;
(3)是以矩形的一边所在直线为旋转轴,其余三边旋转形成的曲面所围成的几何体.
棱锥
(1)底面是多边形,各侧面均是三角形;
(2)各侧面有一个公共顶点.
圆锥
(1)底面是圆;
(2)是以直角三角形的一条直角边所在的直线为旋转轴,其余两边旋转形成的曲面所围成的几何体.
棱台
(1)两底面相互平行;(2)是用一个平行于棱锥底面的平面去截棱锥,底面和截面之间的部分.
圆台
(1)两底面相互平行;
(2)是用一个平行于圆锥底面的平面去截圆锥,底面和截面之间的部分.
球
(1)球心到球面上各点的距离相等;(2)是以半圆的直径所在直线为旋转轴,半圆面旋转一周形成的几何体.
例1下列说法错误的是( ).
A.多面体至少有四个面 B.九棱柱有9条侧棱,9个侧面,侧面为平行四边形
C.长方体、正方体都是棱柱 D.三棱柱的侧面为三角形
答案:D
例2一个棱柱有10个顶点,所有的侧棱长的和为60 cm,则每条侧棱长为___________ cm.
答案:12
例3在本节我们学过的常见几何体中,如果用一个平面去截几何体,如果截面是三角形,那么这个几何体可能是___________.www.21-cn-jy.com
答案:棱锥、棱柱、棱台、圆锥
二、空间几何体的三视图
知识要点:
把光由一点向外散射形成的投影叫中心投影,中心投影的投影线交于一点;把在一束平行光线照射下的投影叫平行投影,平行投影的投影线是平行的.2·1·c·n·j·y
(1)定义:
正视图:光线从几何体的前面向后面正投影得到的投影图;
侧视图:光线从几何体的左面向右面正投影得到的投影图;
俯视图:光线从几何体的上面向下面正投影得到的投影图.
几何体的正视图、侧视图和俯视图统称为几何体的三视图.
(2)三视图中反映的长、宽、高的特点:“长对正”,“高平齐”,“宽相等”.
例1画出下列各几何体的三视图:
答案:
例2 依所给实物图的形状,画出所给组合体的三视图.
答案:图中所给几何体是一个圆柱和一个正六棱柱的组合体,在中心以中心轴为轴线挖去一个小圆柱,故其三视图如下:【来源:21·世纪·教育·网】
例3根据下列图中所给出的一个物体的三视图,试画出它的形状.
答案:所对应的空间几何体的图形为:
三、空间几何体的直观图
知识要点:
“直观图”最常用的画法是斜二测画法,由其规则能画出水平放置的直观图,其实质就是在坐标系中确定点的位置的画法, 基本步骤如下:21·世纪*教育网
(1)建系:在已知图形中取互相垂直的x轴和y轴,得到直角坐标系,直观图中画成斜坐标系,两轴夹角为.www-2-1-cnjy-com
(2)平行不变:已知图形中平行于x轴或y轴的线段,在直观图中分别画成平行于或轴的线段.
(3)长度规则:已知图形中平行于x轴的线段,在直观图中保持长度不变;平行于y轴的线段,长度为原来的一半.2-1-c-n-j-y
四、柱体、锥体、台体的表面积
知识要点:
表面积相关公式
表面积相关公式
棱柱
圆柱
(r:底面半径,h:高)
棱锥
圆锥
(r:底面半径,l:母线长)
棱台
圆台
(r:下底半径,:上底半径,l:母线长)
例1已知圆台的上下底面半径分别是2、5,且侧面面积等于两底面面积之和,求该圆台的母线长.
答案:
例2一个正三棱柱的三视图如右图所示,求这个正三棱柱的表面积.
答案:
五、柱体、锥体、台体的体积
知识要点:
体积公式:
体积公式
体积公式
棱柱
圆柱
棱锥
圆锥
棱台
圆台
柱、椎、台之间,可以看成一个台体进行变化,当台体的上底面逐渐收缩为一个点时,它就成了锥体;当台体的上底面逐渐扩展到与下底面全等时,它就成了柱体.因而体积会有以下的关系:21教育网
.
例1一个长方体的相交于一个顶点的三个面的面积分别是2、3、6,则长方体的体积是 .
答案:6
解析:设长方体的长宽高分别为,则,三式相乘得.所以长方体的体积为6.
例2一块边长为10的正方形铁片按如图所示的阴影部分裁下,然后用余下的四个全等的等腰三角形加工成一个正四棱锥形容器,试建立容器的容积V与x的函数关系式,并求出函数的定义域.21cnjy.com
解:如图,设所截等腰三角形的底边边长为.
在中,,所以,于是.依题意函数的定义域为.
例3一个无盖的圆柱形容器的底面半径为,母线长为6,现将该容器盛满水,然后平稳缓慢地将容器倾斜让水流出,当容器中的水是原来的时,圆柱的母线与水平面所成的角的大小为 .21·cn·jy·com
答案:
解析:容器中水的体积为.流出水的体积为,如图,.设圆柱的母线与水平面所成的角为α,则,解得.
六、球的体积和表面积
知识要点:
表面积: 体积:(R:球的半径).
例1设A、B、C、D是球面上的四个点,且在同一平面内,AB=BC=CD=DA=3,
球心到该平面的距离是球半径的一半,则球的体积是( ).
A. B. C. D.
答案:A
解析:由已知可得,A、B、C、D在球的一个小圆上.∵AB=BC=CD=DA=3,∴四边形为正方形,∴小圆半径.由得,解得.∴球的体积.所以选A.21世纪教育网版权所有
本章总结:
