广西钦州市钦州港区2016-2017学年高二12月月考数学(理)试题
文档属性
| 名称 | 广西钦州市钦州港区2016-2017学年高二12月月考数学(理)试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 249.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-01-05 00:00:00 | ||
图片预览




文档简介
广西钦州市钦州港区2016-2017学年高二年级上学期12月份考试
理科数学试题
(时间:120分钟 满分:120分)
学校:___________姓名:___________班级:___________考号:___________
注意事项:
1.
答题前填写好自己的姓名、班级、考号等信息
2.
请将答案正确填写在答题卡上
一、
选择题
1.
已知抛物线方程为
,直线的方程为
,在抛物线上有一动点P到y轴的距离为
,P到直线的距离为
,则
的最小(
)
A.
B.
C.
D.
2.已知圆
的圆心为抛物线
的焦点,直线
与圆
相切,则该圆的方程为( )
A.
B.
C.
D.
3.已知抛物线
的准线过椭圆
的左焦点且与椭圆交于A、B两点,O为坐标原点,
的面积为
,则椭圆的离心率为(
)
A.
B.
C.
D.
4.设双曲线
=1(
a
>0,
b
>0)的一条渐近线与抛物线
y
=
x
2
+1只有一个公共点,则双曲线的离心率为( ).
A.
B.5
C.
D.
5.已知F
1
、F
2
是双曲线
(a>0,b>0)的两焦点,以线段F
1
F
2
为边作正三角形MF
1
F
2
,若边MF
1
的中点在双曲线上,则双曲线的离心率是 (
)
A.4+
B.
+1
C.
1
D.
6.圆心在
上,半径为3的圆的标准方程为( )
A
B
C
D
7.椭圆
的左、右焦点分别为
,
是
上两点,
,
,则椭圆
的离心率为(
)
A.
B.
C.
D.
8.
已知F为双曲线C:
的左焦点,P,Q为C上的点.若PQ的长等于虚轴长的2倍,点A(5,0)在线段PQ上,则△PQF的周长为(
)
A.11
B.22
C.33
D.44
9.
已知椭圆:
,左右焦点分别为
,过
的直线交椭圆于A,B两点,若
的最大值为5,则
的值是
(
)
A.1
B.
C.
D.
10.长方体
ABCD-A
1
B
1
( http: / / www.21cnjy.com )C
1
D
1
中,
AB
=
AA
1
=2,
AD
=1,
E
为
CC
1
的中点,则异面直线
BC
1
与
AE
所成角的余弦值为
( ).
A.
B.
C.
D.
11.设
是正三棱锥,
是
的重心,
是
上的一点,且
,若
,则
为(
)
A.
B.
C.
D.
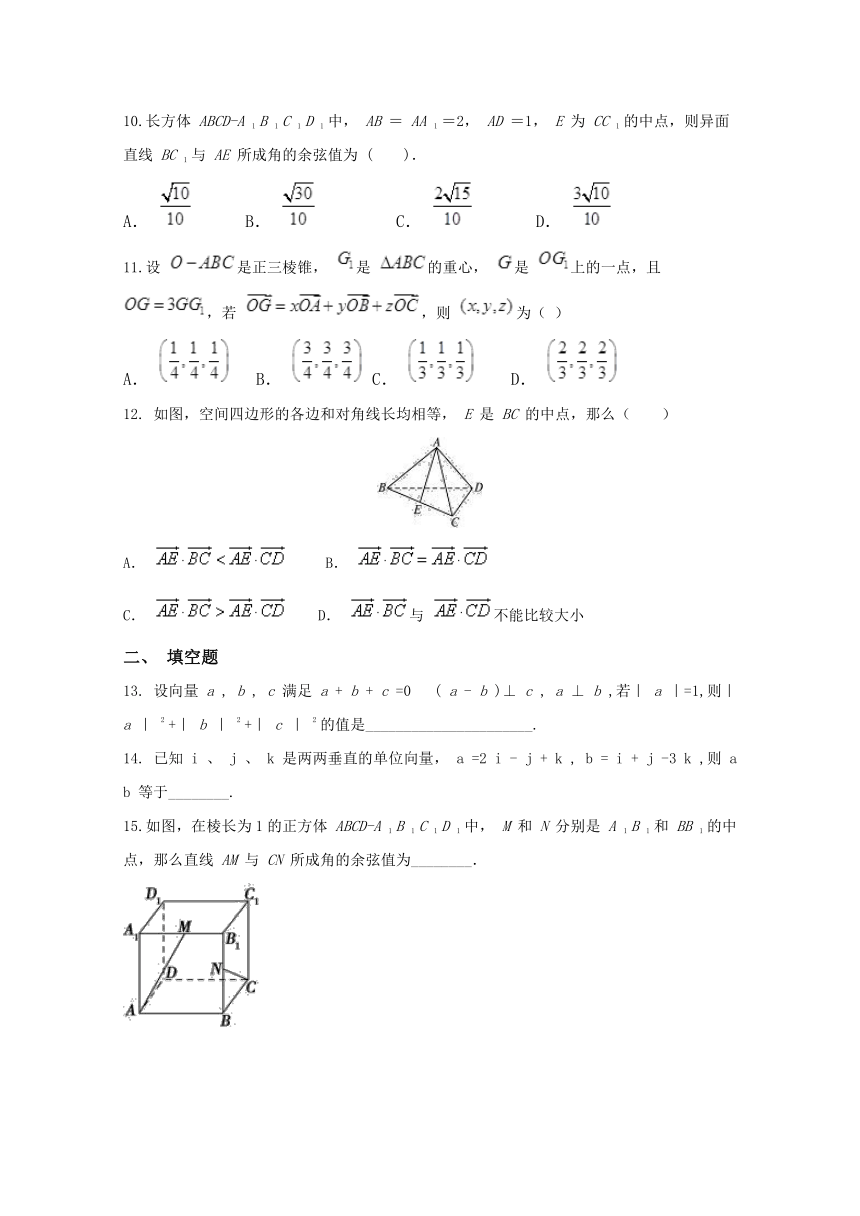
12.
如图,空间四边形的各边和对角线长均相等,
E
是
BC
的中点,那么( )
( http: / / www.21cnjy.com )
A.
B.
C.
D.
与
不能比较大小
二、
填空题
13.
设向量
a
,
b
,
c
满足
( http: / / www.21cnjy.com )a
+
b
+
c
=0
(
a
-
b
)⊥
c
,
a
⊥
b
,若|
a
|=1,则|
a
|
2
+|
b
|
2
+|
c
|
2
的值是______________________.
14.
已知
i
、
j
、
k
是两两垂
( http: / / www.21cnjy.com )直的单位向量,
a
=2
i
-
j
+
k
,
b
=
i
+
j
-3
k
,则
a
b
等于________.
15.如图,在棱长为1的正方体
ABCD-A
1
B
1
C
1
D
1
中,
M
和
N
分别是
A
1
B
1
和
BB
1
的中点,那么直线
AM
与
CN
所成角的余弦值为________.
( http: / / www.21cnjy.com )
16.已知
、
分别为双曲线
:
的左、右焦点,点
,点
的坐标为(2,0),
为
的平分线.则
.
17.
若一个二面角的两个面的法向量分别为
m
=(0,0,3),
n
=(8,9,2),则这个二面角的余弦值为________.
三、
解答题
18.
已知动点
到定点
的距离与到定直线:
的距离相等,点C在直线上。
(1)求动点
的轨迹方程。
(2)设过定点
,且法向量
的直线与(1)中的轨迹相交于
两点且点
在
轴的上方。判断
能否为钝角并说明理由。进一步研究
为钝角时点
纵坐标的取值范围。
19.已知椭圆方程为
,射线
(x≥0)与椭圆的交点为M,过M作倾斜角互补的两条直线,分别与椭圆交于A、B两点(异于M).
(Ⅰ)求证直线AB的斜率为定值;
(Ⅱ)求△
面积的最大值.
20.已知双曲线
,
、
是双曲线的左右顶点,
是双曲线上除两顶点外的一点,直线
与直线
的斜率之积是
,
求双曲线的离心率;
若该双曲线的焦点到渐近线的距离是
,求双曲线的方程.
21.
正三棱柱
ABC
A
1
B
1
C
1
的底面边长为
a
,侧棱长为
a
,求
AC
1
与侧面
ABB
1
A
1
所成的角.
22.
若
PA
⊥平面
ABC
,
AC
⊥
BC
,
PA
=
AC
=1,
BC
=
,求二面角
APBC
的余弦值.
答案
一、选择题
1、
D2、B
3、C
4、D
5、B
6、B
7、D
8、
D9、
D10、B
11、A
12、C
二、填空题
13、4
14、-2
15、
16、
6
17、或-
三、解答题
18、
( http: / / www.21cnjy.com )
解(1)动点
到定点
的距离与到定直线:
的距离相等,所以
的轨迹是以点
为焦点,直线为准线的抛物线,轨迹方程为
(2)方法一:由题意,直线
的方程为
故A、B两点的坐标满足方程组
得
,
设
,则
,
由
,所以
不可能为钝角。
若
为钝角时,
,
得
若
为钝角时,点C纵坐标的取值范围是
注:忽略
扣1分
方法二:由题意,直线
的方程为
(5分)
故A、B两点的坐标满足方程组
得
,
设
,则
,
由
,所以
不可能为钝角。
过
垂直于直线
的直线方程为
令
得
为钝角时,点C纵坐标的取值范围是
注:忽略
扣1分
19、
(Ⅰ)∵斜率k存在,不妨设k>0,求出M(
,2).
直线MA方程为
,
分别与椭圆方程联立,可解出
,
同理得,直线MB方程为
.
∴
,为定值.
(Ⅱ)设直线AB方程为
,与
联立,消去y得
.
由
>0得一4<m<4,且m≠0,
点M到AB的距离为
.
设△AMB的面积为S. ∴
.
当
时,得
.
20、
(1)
;(2)
.
21、
( http: / / www.21cnjy.com )
解法一:
建立如图所示的空间直角坐标系,则
A
(0,0,0),
B
(0,
a
,0),
A
1
(0,0,
a
),
C
1
(-
,
,
a
),取
A
1
B
1
的中点
M
,则
M
(0,
,
a
),连结
AM
、
MC
1
,有
=(0,
a
,0),
=(0,0,
a
).
由于
∴
MC
1
⊥面
ABB
1
A
1
.
∴∠
C
1
AM
是
AC
1
与侧面
A
1
B
所成的角.
∵
∴
而
∴
( http: / / www.21cnjy.com )
∴〈
〉=30°,即
AC
1
与侧面
AB
1
所成的角为30°.
解法二:
(法向量法)(接方法一)
=(0,0,
a
).
设侧面
A
1
B
的法向量
n
=(λ,
x
,
y
),
∴
n
=0且
n
=0.∴
ax
=0,且
ay
=0.
∴
x
=
y
=0.故
n
=(λ,0,0).
∵
∴
( http: / / www.21cnjy.com )
∴|cos〈
,
n
〉|=
.
∴〈
〉=30°,即
AC
1
与侧面
AB
1
所成的角为30°.
绿色通道:
充分利用图形的几何特征建立
( http: / / www.21cnjy.com )适当的空间直角坐标系,再用向量的有关知识求解线面角.方法二给出了一般的方法,先求平面法向量与斜线夹角,再进行换算.
22、
( http: / / www.21cnjy.com )
解法一
:
如图所示,取
PB
的中点
D
,连结
CD
.∵
PC
=
BC
=
,
∴
CD
⊥
PB
.
∴作
AE
⊥
PB
于E,那么二面角
APBC
的大小就等于异面直线
DC
与
EA
所成的角
θ
的大小.
∵
PD
=1,
PE
=
,
∴
DE
=
PD
-
PE
=
.
又∵
AE
=
CD
=1,
AC
=1,
∴
cos(π-
θ
),
即1=
+1-2
1cos
θ
,
解得cos
θ
=
.
故二面角
APBC
的余弦值为
.
解法二
:
由解法一可知,向量
的夹角的大小就是二面角
APBC
的大小,如上图,建立空间直角坐标系
C
xyz
,则
A
(1,0,0),
B
(0,
,0),C(0,0,0),
P
(1,0,1),
D
为
PB
的中点,
D
(
).
∴
,即
E
分
的比为
.
∴
E
(
),
∴
故二面角A
P
BC的余弦值为
.
( http: / / www.21cnjy.com )
解法三
:
如图所示建立空间直角坐标系,则
A
(0,0,0),
B
(
,1,0),
C
(0,1,0),
P
(0,0,1),
=(0,0,1),
=(
,1,0),
=(2,0,0),
=(0,-1,1),
设平面
PAB
的法向量为
m
=(
x
,
y
,
z
),则
令
x
=1,则
m
=(1,-
,0).
设平面
PBC
的法向量为
n
=(
x
′,
y
′,
z
′),则
令
y
′=-1,则
n
=(0,-1,-1),
∴cos〈
m
,
n
〉=
∴二面角
APBC
的余弦值为
.
绿色通道:
(1)求二面角的大小,可以在两个半平面内作出垂直于棱的两个向量,转化为这两向量的夹角,但应注意两向量的始点应在二面角的棱上.
(2)当空间直角坐标系容易建立(有特殊
( http: / / www.21cnjy.com )的位置关系)时,用向量法解较为简捷、明快.用法向量求二面角的大小时,有时不易判断两法向量的夹角的大小就是二面角的大小(相等或互补),但我们完全可以根据图形观察得到结论,这是因为二面角是钝二面角还是锐二面角一般是明显的.
理科数学试题
(时间:120分钟 满分:120分)
学校:___________姓名:___________班级:___________考号:___________
注意事项:
1.
答题前填写好自己的姓名、班级、考号等信息
2.
请将答案正确填写在答题卡上
一、
选择题
1.
已知抛物线方程为
,直线的方程为
,在抛物线上有一动点P到y轴的距离为
,P到直线的距离为
,则
的最小(
)
A.
B.
C.
D.
2.已知圆
的圆心为抛物线
的焦点,直线
与圆
相切,则该圆的方程为( )
A.
B.
C.
D.
3.已知抛物线
的准线过椭圆
的左焦点且与椭圆交于A、B两点,O为坐标原点,
的面积为
,则椭圆的离心率为(
)
A.
B.
C.
D.
4.设双曲线
=1(
a
>0,
b
>0)的一条渐近线与抛物线
y
=
x
2
+1只有一个公共点,则双曲线的离心率为( ).
A.
B.5
C.
D.
5.已知F
1
、F
2
是双曲线
(a>0,b>0)的两焦点,以线段F
1
F
2
为边作正三角形MF
1
F
2
,若边MF
1
的中点在双曲线上,则双曲线的离心率是 (
)
A.4+
B.
+1
C.
1
D.
6.圆心在
上,半径为3的圆的标准方程为( )
A
B
C
D
7.椭圆
的左、右焦点分别为
,
是
上两点,
,
,则椭圆
的离心率为(
)
A.
B.
C.
D.
8.
已知F为双曲线C:
的左焦点,P,Q为C上的点.若PQ的长等于虚轴长的2倍,点A(5,0)在线段PQ上,则△PQF的周长为(
)
A.11
B.22
C.33
D.44
9.
已知椭圆:
,左右焦点分别为
,过
的直线交椭圆于A,B两点,若
的最大值为5,则
的值是
(
)
A.1
B.
C.
D.
10.长方体
ABCD-A
1
B
1
( http: / / www.21cnjy.com )C
1
D
1
中,
AB
=
AA
1
=2,
AD
=1,
E
为
CC
1
的中点,则异面直线
BC
1
与
AE
所成角的余弦值为
( ).
A.
B.
C.
D.
11.设
是正三棱锥,
是
的重心,
是
上的一点,且
,若
,则
为(
)
A.
B.
C.
D.
12.
如图,空间四边形的各边和对角线长均相等,
E
是
BC
的中点,那么( )
( http: / / www.21cnjy.com )
A.
B.
C.
D.
与
不能比较大小
二、
填空题
13.
设向量
a
,
b
,
c
满足
( http: / / www.21cnjy.com )a
+
b
+
c
=0
(
a
-
b
)⊥
c
,
a
⊥
b
,若|
a
|=1,则|
a
|
2
+|
b
|
2
+|
c
|
2
的值是______________________.
14.
已知
i
、
j
、
k
是两两垂
( http: / / www.21cnjy.com )直的单位向量,
a
=2
i
-
j
+
k
,
b
=
i
+
j
-3
k
,则
a
b
等于________.
15.如图,在棱长为1的正方体
ABCD-A
1
B
1
C
1
D
1
中,
M
和
N
分别是
A
1
B
1
和
BB
1
的中点,那么直线
AM
与
CN
所成角的余弦值为________.
( http: / / www.21cnjy.com )
16.已知
、
分别为双曲线
:
的左、右焦点,点
,点
的坐标为(2,0),
为
的平分线.则
.
17.
若一个二面角的两个面的法向量分别为
m
=(0,0,3),
n
=(8,9,2),则这个二面角的余弦值为________.
三、
解答题
18.
已知动点
到定点
的距离与到定直线:
的距离相等,点C在直线上。
(1)求动点
的轨迹方程。
(2)设过定点
,且法向量
的直线与(1)中的轨迹相交于
两点且点
在
轴的上方。判断
能否为钝角并说明理由。进一步研究
为钝角时点
纵坐标的取值范围。
19.已知椭圆方程为
,射线
(x≥0)与椭圆的交点为M,过M作倾斜角互补的两条直线,分别与椭圆交于A、B两点(异于M).
(Ⅰ)求证直线AB的斜率为定值;
(Ⅱ)求△
面积的最大值.
20.已知双曲线
,
、
是双曲线的左右顶点,
是双曲线上除两顶点外的一点,直线
与直线
的斜率之积是
,
求双曲线的离心率;
若该双曲线的焦点到渐近线的距离是
,求双曲线的方程.
21.
正三棱柱
ABC
A
1
B
1
C
1
的底面边长为
a
,侧棱长为
a
,求
AC
1
与侧面
ABB
1
A
1
所成的角.
22.
若
PA
⊥平面
ABC
,
AC
⊥
BC
,
PA
=
AC
=1,
BC
=
,求二面角
APBC
的余弦值.
答案
一、选择题
1、
D2、B
3、C
4、D
5、B
6、B
7、D
8、
D9、
D10、B
11、A
12、C
二、填空题
13、4
14、-2
15、
16、
6
17、或-
三、解答题
18、
( http: / / www.21cnjy.com )
解(1)动点
到定点
的距离与到定直线:
的距离相等,所以
的轨迹是以点
为焦点,直线为准线的抛物线,轨迹方程为
(2)方法一:由题意,直线
的方程为
故A、B两点的坐标满足方程组
得
,
设
,则
,
由
,所以
不可能为钝角。
若
为钝角时,
,
得
若
为钝角时,点C纵坐标的取值范围是
注:忽略
扣1分
方法二:由题意,直线
的方程为
(5分)
故A、B两点的坐标满足方程组
得
,
设
,则
,
由
,所以
不可能为钝角。
过
垂直于直线
的直线方程为
令
得
为钝角时,点C纵坐标的取值范围是
注:忽略
扣1分
19、
(Ⅰ)∵斜率k存在,不妨设k>0,求出M(
,2).
直线MA方程为
,
分别与椭圆方程联立,可解出
,
同理得,直线MB方程为
.
∴
,为定值.
(Ⅱ)设直线AB方程为
,与
联立,消去y得
.
由
>0得一4<m<4,且m≠0,
点M到AB的距离为
.
设△AMB的面积为S. ∴
.
当
时,得
.
20、
(1)
;(2)
.
21、
( http: / / www.21cnjy.com )
解法一:
建立如图所示的空间直角坐标系,则
A
(0,0,0),
B
(0,
a
,0),
A
1
(0,0,
a
),
C
1
(-
,
,
a
),取
A
1
B
1
的中点
M
,则
M
(0,
,
a
),连结
AM
、
MC
1
,有
=(0,
a
,0),
=(0,0,
a
).
由于
∴
MC
1
⊥面
ABB
1
A
1
.
∴∠
C
1
AM
是
AC
1
与侧面
A
1
B
所成的角.
∵
∴
而
∴
( http: / / www.21cnjy.com )
∴〈
〉=30°,即
AC
1
与侧面
AB
1
所成的角为30°.
解法二:
(法向量法)(接方法一)
=(0,0,
a
).
设侧面
A
1
B
的法向量
n
=(λ,
x
,
y
),
∴
n
=0且
n
=0.∴
ax
=0,且
ay
=0.
∴
x
=
y
=0.故
n
=(λ,0,0).
∵
∴
( http: / / www.21cnjy.com )
∴|cos〈
,
n
〉|=
.
∴〈
〉=30°,即
AC
1
与侧面
AB
1
所成的角为30°.
绿色通道:
充分利用图形的几何特征建立
( http: / / www.21cnjy.com )适当的空间直角坐标系,再用向量的有关知识求解线面角.方法二给出了一般的方法,先求平面法向量与斜线夹角,再进行换算.
22、
( http: / / www.21cnjy.com )
解法一
:
如图所示,取
PB
的中点
D
,连结
CD
.∵
PC
=
BC
=
,
∴
CD
⊥
PB
.
∴作
AE
⊥
PB
于E,那么二面角
APBC
的大小就等于异面直线
DC
与
EA
所成的角
θ
的大小.
∵
PD
=1,
PE
=
,
∴
DE
=
PD
-
PE
=
.
又∵
AE
=
CD
=1,
AC
=1,
∴
cos(π-
θ
),
即1=
+1-2
1cos
θ
,
解得cos
θ
=
.
故二面角
APBC
的余弦值为
.
解法二
:
由解法一可知,向量
的夹角的大小就是二面角
APBC
的大小,如上图,建立空间直角坐标系
C
xyz
,则
A
(1,0,0),
B
(0,
,0),C(0,0,0),
P
(1,0,1),
D
为
PB
的中点,
D
(
).
∴
,即
E
分
的比为
.
∴
E
(
),
∴
故二面角A
P
BC的余弦值为
.
( http: / / www.21cnjy.com )
解法三
:
如图所示建立空间直角坐标系,则
A
(0,0,0),
B
(
,1,0),
C
(0,1,0),
P
(0,0,1),
=(0,0,1),
=(
,1,0),
=(2,0,0),
=(0,-1,1),
设平面
PAB
的法向量为
m
=(
x
,
y
,
z
),则
令
x
=1,则
m
=(1,-
,0).
设平面
PBC
的法向量为
n
=(
x
′,
y
′,
z
′),则
令
y
′=-1,则
n
=(0,-1,-1),
∴cos〈
m
,
n
〉=
∴二面角
APBC
的余弦值为
.
绿色通道:
(1)求二面角的大小,可以在两个半平面内作出垂直于棱的两个向量,转化为这两向量的夹角,但应注意两向量的始点应在二面角的棱上.
(2)当空间直角坐标系容易建立(有特殊
( http: / / www.21cnjy.com )的位置关系)时,用向量法解较为简捷、明快.用法向量求二面角的大小时,有时不易判断两法向量的夹角的大小就是二面角的大小(相等或互补),但我们完全可以根据图形观察得到结论,这是因为二面角是钝二面角还是锐二面角一般是明显的.
同课章节目录
