18.2.2 由对角线的关系判定平行四边形 课件
文档属性
| 名称 | 18.2.2 由对角线的关系判定平行四边形 课件 |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-01-04 20:31:01 | ||
图片预览




文档简介
课件26张PPT。18.2.2 由对角线的关系判定平行四边形1课堂讲解由对角线互相平分判定平行四边形
平行四边形判定方法的综合应用2课时流程逐点
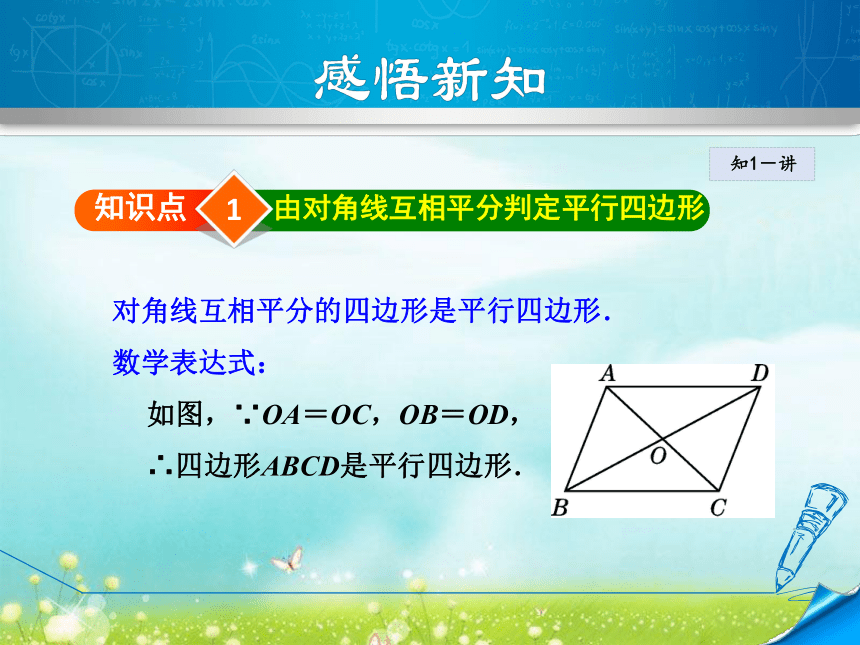
导讲练课堂小结作业提升平行四边形的判定方法有哪些?复习回顾1知识点由对角线互相平分判定平行四边形 知1-讲对角线互相平分的四边形是平行四边形.
数学表达式:
如图,∵OA=OC,OB=OD,
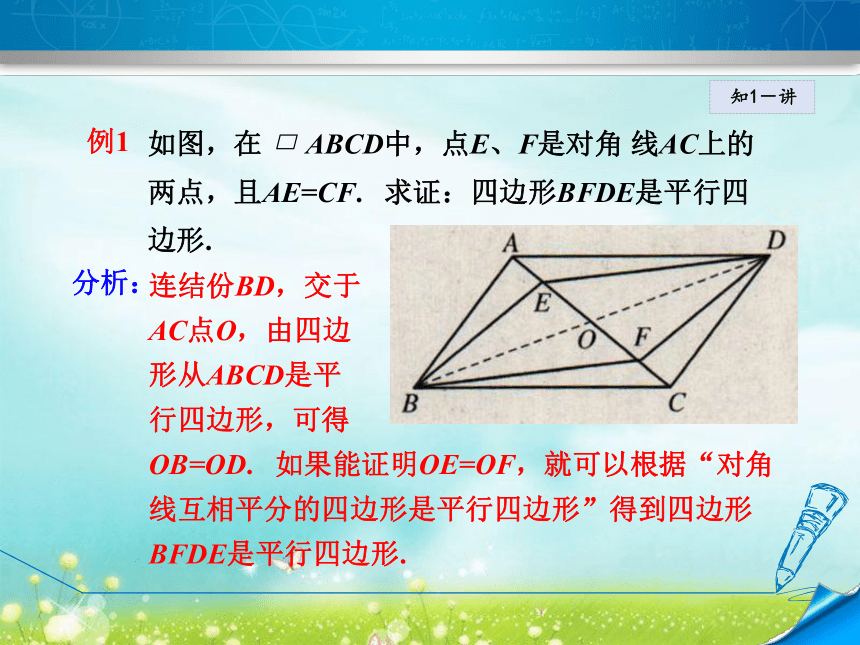
∴四边形ABCD是平行四边形.知1-讲例1 如图,在 ABCD中,点E、F是对角 线AC上的
两点,且AE=CF. 求证:四边形BFDE是平行四
边形.连结份BD,交于
AC点O,由四边
形从ABCD是平
行四边形,可得
OB=OD. 如果能证明OE=OF,就可以根据“对角
线互相平分的四边形是平行四边形”得到四边形
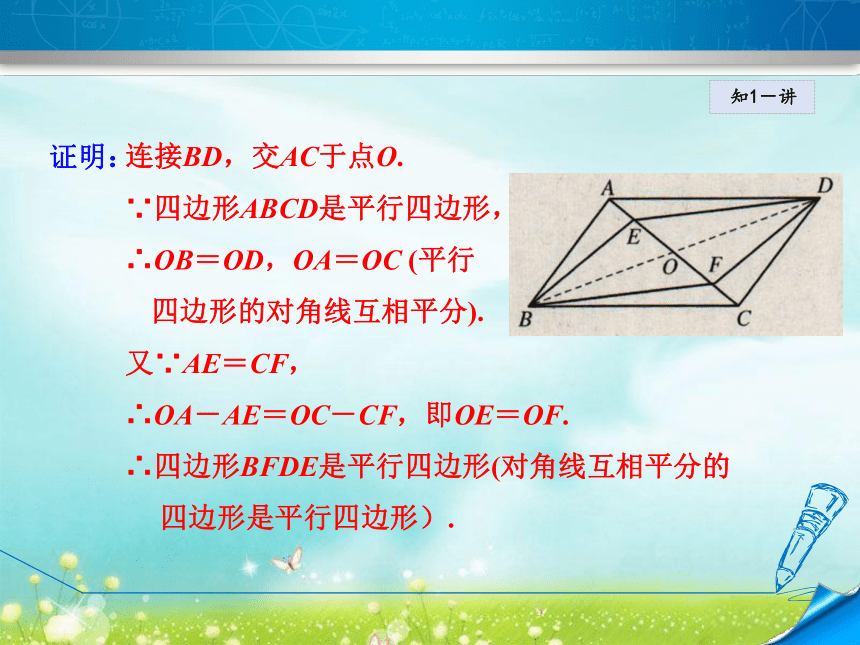
BFDE是平行四边形.分析:知1-讲证明:连接BD,交AC于点O.
∵四边形ABCD是平行四边形,
∴OB=OD,OA=OC (平行
四边形的对角线互相平分).
又∵AE=CF,
∴OA-AE=OC-CF,即OE=OF.
∴四边形BFDE是平行四边形(对角线互相平分的
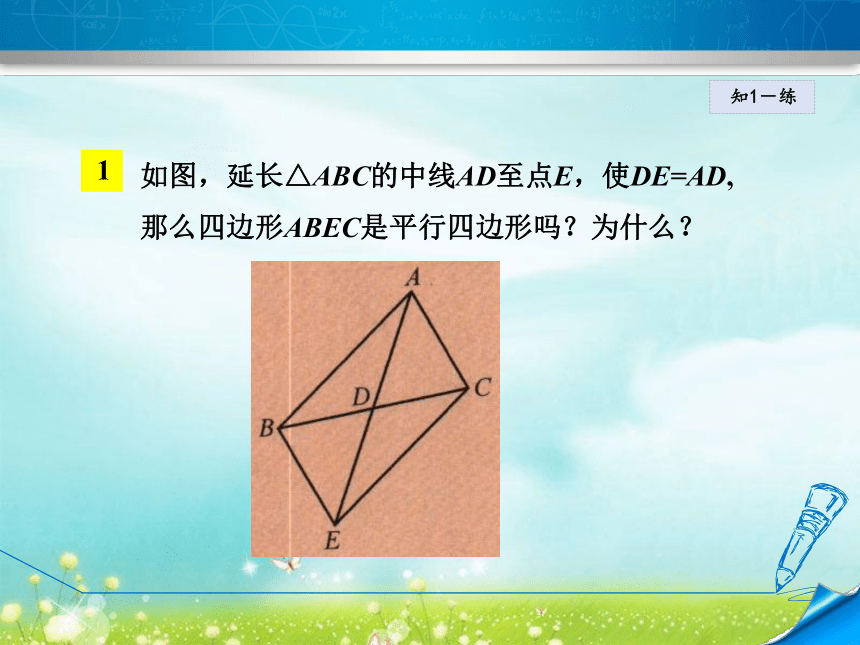
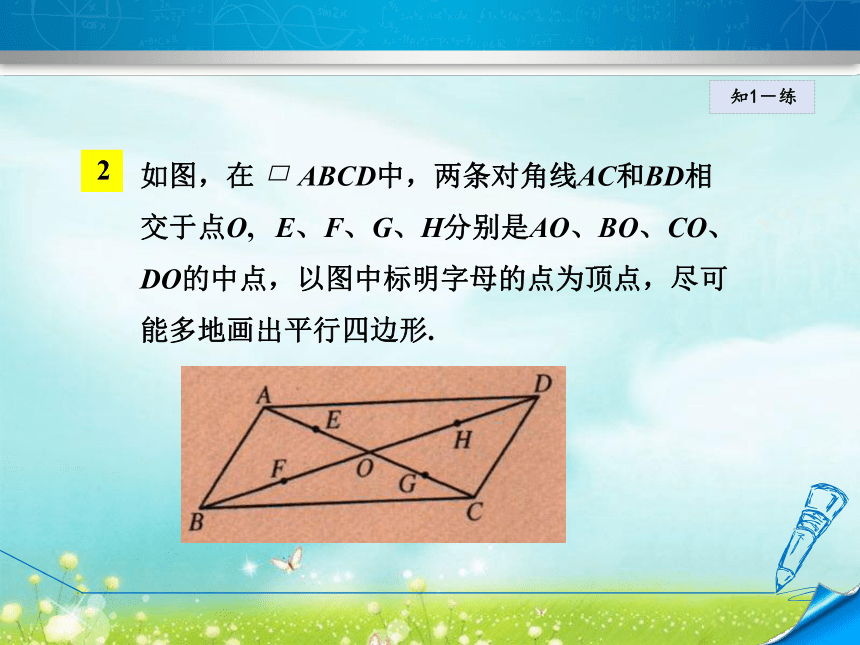
四边形是平行四边形).知1-练如图,延长△ABC的中线AD至点E,使DE=AD, 那么四边形ABEC是平行四边形吗?为什么?知1-练如图,在 ABCD中,两条对角线AC和BD相交于点O, E、F、G、H分别是AO、BO、CO、DO的中点,以图中标明字母的点为顶点,尽可能多地画出平行四边形.知1-练如图,在四边形ABCD中,对角线AC,BD相交于点O,下列条件不能判定四边形ABCD为平行四边形的是( )
A.AB∥CD,AD∥BC
B.OA=OC,OB=OD
C.AD=BC,AB∥CD
D.AB=CD,AD=BC知1-练如图所示,点E,F在?ABCD的对角线AC上,添
加一个条件仍不能判定四边形BEDF为平行四边
形的是( )
A.AE=CF
B.AF=CE
C.∠ABE=∠CDF
D.BE=DF2知识点平行四边形判定方法的综合应用知2-讲1.平行四边形的判定方法:
(1)定义:两组对边分别平行的四边形是平行四边形.
(2)两组对边分别相等的四边形是平行四边形.
(3)一组对边平行且相等的四边形是平行四边形.
(4)两组对角分别相等的四边形是平行四边形.
(5)对角线互相平分的四边形是平行四边形.要点精析:
(1)判定平行四边形的五种方法各有妙用,应仔细观
察题图所给条件,看它与哪种方法接近,灵活选
择适合题目的判定方法;
(2)这五种方法与平行四边形的性质相呼应,每一种
方法都对应着一条性质,要注意它们的区别与联
系.
①由平行四边形这一条件得到边、角、对角线关
系是性质;
②由边、角、对角线关系得到平行四边形是判定.知2-讲2. 易错警示:判定平行四边形需要两个独立条件,
但“两组邻边分别相等”“两组邻角分别相等”
“一组对边平行,另一组对边相等”这三种情况
都不能判定平行四边形.知2-讲例2 知2-讲 如图,四边形ABCD是平行四边形,E,F为对角线AC上两点,连接ED,EB,FD,FB.给出以下结论:①BE∥DF;②BE=DF;③AE=CF.请你从中选取一个条件,使∠1=∠2成立,并给出证明.导引:欲证明∠1=∠2,只需证得
四边形EDFB是平行四边形
或△ABF≌△CDE即可.知2-讲(1)补充条件①BE∥DF.
∵BE∥DF,
∴∠BEC=∠DFA. ∴∠BEA=∠DFC.
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD. ∴∠BAE=∠DCF.
在△ABE与△CDF中,
∴△ABE≌△CDF(AAS).
∴BE=DF. ∴四边形BFDE是平行四边形.
∴ED∥BF. ∴∠1=∠2.解:证明:知2-讲(2)补充条件③AE=CF.
证明:∵AE=CF,∴AF=CE.
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD.
∴∠BAF=∠DCE.
在△ABF与△CDE中,
∴△ABF≌△CDE(SAS).
∴∠1=∠2.例3 知2-讲如图,在?ABCD中,延长AB到E,延长CD到F,使得BE=DF,试猜测AC与EF有什么关系,并
加以证明.知2-讲导引:两条线段的数量关系有相等或倍分,位置关系
有平行或相交,而相交的特殊情况有垂直、互
相平分,如图,连接AF,CE,分析本题可证
四边形AECF是平行四边形,则AC与EF互相
平分.知2-讲解:AC与EF互相平分.
方法一:连接AF,CE,如图.
∵四边形ABCD是平行四边形,
∴DC=AB,CF∥AE,
∴∠CFE=∠AEF.
∵DF=BE,∴CF=AE.
又∵EF=FE,∴△CFE≌△AEF,
∴∠CEF=∠AFE,∴CE∥AF,
∴四边形AECF是平行四边形(两组对边分别平行的
四边形是平行四边形).∴AC与EF互相平分.知2-讲方法二:连接AF,CE,如图.
∵四边形ABCD是平行四边形,
∴DC∥AB,DC=AB.
∵DF=BE,∴CF=AE.
又∵CF∥AE,
∴四边形AECF为平行四边形(一组对边平行且相等
的四边形是平行四边形),
∴AC与EF互相平分.知2-讲 猜测两条线段的位置关系时,一般为特殊关系,
由图形可以直接看出.证明两条线段互相平分,可以
证明线段所在的三角形全等,也可以转化成证明线段
所在的四边形是平行四边形;在有四边形的问题中,
其首选的方法是先判定四边形是平行四边形,再利用
平行四边形的性质解决问题.1 在四边形ABCD中,AC交BD于点O,且AB∥CD,给出以下四种说法:
①如果再加上条件“BC=AD”,那么四边形ABCD一定是平行四边形;②如果再加上条件“∠BAD=∠BCD”,那么四边形ABCD一定是平行四边形;③如果再加上条件“AO=OC”,那么四边形ABCD一定是平行四边形; ④如果再加上条件“∠DBA=∠CAB”,那么四边形ABCD一定是平行四边形.
其中正确的说法是( )
A.①② B.①③④ C.②③ D.②③④知2-练2 下列说法错误的是( )
A.对角线互相平分的四边形是平行四边形
B.两组对边分别相等的四边形是平行四边形
C.一组对边平行且相等的四边形是平行四边形
D.一组对边相等,另一组对边平行的四边形是平行四边形知2-练知2-练四边形ABCD中,对角线AC、BD相交
于点O,给出下列四个条件:① AD∥BC;② AD
=BC;③ OA=OC;④ OB=OD,从中任选两个
条件,能使四边形ABCD为平行四边形的选法有
( )
A.3种 B.4种
C.5种 D.6种平行四边形的判定方法:
(1)定义:两组对边分别平行的四边形是平行四边形.
(2)两组对边分别相等的四边形是平行四边形.
(3)一组对边平行且相等的四边形是平行四边形.
(4)两组对角分别相等的四边形是平行四边形.
(5)对角线互相平分的四边形是平行四边形.必做: 完成教材P87练习T3,
P91习题18.2T5
2. 补充: 请完成练习册剩余部分习题
平行四边形判定方法的综合应用2课时流程逐点
导讲练课堂小结作业提升平行四边形的判定方法有哪些?复习回顾1知识点由对角线互相平分判定平行四边形 知1-讲对角线互相平分的四边形是平行四边形.
数学表达式:
如图,∵OA=OC,OB=OD,
∴四边形ABCD是平行四边形.知1-讲例1 如图,在 ABCD中,点E、F是对角 线AC上的
两点,且AE=CF. 求证:四边形BFDE是平行四
边形.连结份BD,交于
AC点O,由四边
形从ABCD是平
行四边形,可得
OB=OD. 如果能证明OE=OF,就可以根据“对角
线互相平分的四边形是平行四边形”得到四边形
BFDE是平行四边形.分析:知1-讲证明:连接BD,交AC于点O.
∵四边形ABCD是平行四边形,
∴OB=OD,OA=OC (平行
四边形的对角线互相平分).
又∵AE=CF,
∴OA-AE=OC-CF,即OE=OF.
∴四边形BFDE是平行四边形(对角线互相平分的
四边形是平行四边形).知1-练如图,延长△ABC的中线AD至点E,使DE=AD, 那么四边形ABEC是平行四边形吗?为什么?知1-练如图,在 ABCD中,两条对角线AC和BD相交于点O, E、F、G、H分别是AO、BO、CO、DO的中点,以图中标明字母的点为顶点,尽可能多地画出平行四边形.知1-练如图,在四边形ABCD中,对角线AC,BD相交于点O,下列条件不能判定四边形ABCD为平行四边形的是( )
A.AB∥CD,AD∥BC
B.OA=OC,OB=OD
C.AD=BC,AB∥CD
D.AB=CD,AD=BC知1-练如图所示,点E,F在?ABCD的对角线AC上,添
加一个条件仍不能判定四边形BEDF为平行四边
形的是( )
A.AE=CF
B.AF=CE
C.∠ABE=∠CDF
D.BE=DF2知识点平行四边形判定方法的综合应用知2-讲1.平行四边形的判定方法:
(1)定义:两组对边分别平行的四边形是平行四边形.
(2)两组对边分别相等的四边形是平行四边形.
(3)一组对边平行且相等的四边形是平行四边形.
(4)两组对角分别相等的四边形是平行四边形.
(5)对角线互相平分的四边形是平行四边形.要点精析:
(1)判定平行四边形的五种方法各有妙用,应仔细观
察题图所给条件,看它与哪种方法接近,灵活选
择适合题目的判定方法;
(2)这五种方法与平行四边形的性质相呼应,每一种
方法都对应着一条性质,要注意它们的区别与联
系.
①由平行四边形这一条件得到边、角、对角线关
系是性质;
②由边、角、对角线关系得到平行四边形是判定.知2-讲2. 易错警示:判定平行四边形需要两个独立条件,
但“两组邻边分别相等”“两组邻角分别相等”
“一组对边平行,另一组对边相等”这三种情况
都不能判定平行四边形.知2-讲例2 知2-讲 如图,四边形ABCD是平行四边形,E,F为对角线AC上两点,连接ED,EB,FD,FB.给出以下结论:①BE∥DF;②BE=DF;③AE=CF.请你从中选取一个条件,使∠1=∠2成立,并给出证明.导引:欲证明∠1=∠2,只需证得
四边形EDFB是平行四边形
或△ABF≌△CDE即可.知2-讲(1)补充条件①BE∥DF.
∵BE∥DF,
∴∠BEC=∠DFA. ∴∠BEA=∠DFC.
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD. ∴∠BAE=∠DCF.
在△ABE与△CDF中,
∴△ABE≌△CDF(AAS).
∴BE=DF. ∴四边形BFDE是平行四边形.
∴ED∥BF. ∴∠1=∠2.解:证明:知2-讲(2)补充条件③AE=CF.
证明:∵AE=CF,∴AF=CE.
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD.
∴∠BAF=∠DCE.
在△ABF与△CDE中,
∴△ABF≌△CDE(SAS).
∴∠1=∠2.例3 知2-讲如图,在?ABCD中,延长AB到E,延长CD到F,使得BE=DF,试猜测AC与EF有什么关系,并
加以证明.知2-讲导引:两条线段的数量关系有相等或倍分,位置关系
有平行或相交,而相交的特殊情况有垂直、互
相平分,如图,连接AF,CE,分析本题可证
四边形AECF是平行四边形,则AC与EF互相
平分.知2-讲解:AC与EF互相平分.
方法一:连接AF,CE,如图.
∵四边形ABCD是平行四边形,
∴DC=AB,CF∥AE,
∴∠CFE=∠AEF.
∵DF=BE,∴CF=AE.
又∵EF=FE,∴△CFE≌△AEF,
∴∠CEF=∠AFE,∴CE∥AF,
∴四边形AECF是平行四边形(两组对边分别平行的
四边形是平行四边形).∴AC与EF互相平分.知2-讲方法二:连接AF,CE,如图.
∵四边形ABCD是平行四边形,
∴DC∥AB,DC=AB.
∵DF=BE,∴CF=AE.
又∵CF∥AE,
∴四边形AECF为平行四边形(一组对边平行且相等
的四边形是平行四边形),
∴AC与EF互相平分.知2-讲 猜测两条线段的位置关系时,一般为特殊关系,
由图形可以直接看出.证明两条线段互相平分,可以
证明线段所在的三角形全等,也可以转化成证明线段
所在的四边形是平行四边形;在有四边形的问题中,
其首选的方法是先判定四边形是平行四边形,再利用
平行四边形的性质解决问题.1 在四边形ABCD中,AC交BD于点O,且AB∥CD,给出以下四种说法:
①如果再加上条件“BC=AD”,那么四边形ABCD一定是平行四边形;②如果再加上条件“∠BAD=∠BCD”,那么四边形ABCD一定是平行四边形;③如果再加上条件“AO=OC”,那么四边形ABCD一定是平行四边形; ④如果再加上条件“∠DBA=∠CAB”,那么四边形ABCD一定是平行四边形.
其中正确的说法是( )
A.①② B.①③④ C.②③ D.②③④知2-练2 下列说法错误的是( )
A.对角线互相平分的四边形是平行四边形
B.两组对边分别相等的四边形是平行四边形
C.一组对边平行且相等的四边形是平行四边形
D.一组对边相等,另一组对边平行的四边形是平行四边形知2-练知2-练四边形ABCD中,对角线AC、BD相交
于点O,给出下列四个条件:① AD∥BC;② AD
=BC;③ OA=OC;④ OB=OD,从中任选两个
条件,能使四边形ABCD为平行四边形的选法有
( )
A.3种 B.4种
C.5种 D.6种平行四边形的判定方法:
(1)定义:两组对边分别平行的四边形是平行四边形.
(2)两组对边分别相等的四边形是平行四边形.
(3)一组对边平行且相等的四边形是平行四边形.
(4)两组对角分别相等的四边形是平行四边形.
(5)对角线互相平分的四边形是平行四边形.必做: 完成教材P87练习T3,
P91习题18.2T5
2. 补充: 请完成练习册剩余部分习题
