18.2.3 平行四边形的性质和判定的应用 课件
文档属性
| 名称 | 18.2.3 平行四边形的性质和判定的应用 课件 |  | |
| 格式 | zip | ||
| 文件大小 | 666.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-01-04 20:32:59 | ||
图片预览







文档简介
课件22张PPT。18.2.3 平行四边形的性质和判定的应用名师点金平行四边形的性质与判定方法的区别与联系.
(1)联系:平行四边形的性质的题设和结论正好与判定
的题设和结论相反,它们构成互逆的关系.
(2)区别:由平行四边形这一条件得到边、角或对角线
的关系,这是平行四边形的性质;反之,由边、角
或对角线的关系得到平行四边形,这是平行四边形
的判定.1类型利用平行四边形的性质和判定判定平行四边形1.如图,在?ABCD中,E,F分别是AB,
CD的中点.
(1)求证:四边形EBFD为平行四边形;
(2)对角线AC分别与DE,BF交于点M,N,求证:
△ABN≌△CDM.(1)∵四边形ABCD为平行四边形,
∴AB=CD,EB∥DF.
又∵E,F分别是AB,CD的中点,
∴EB= AB,DF= CD.
∴EB=DF.
∴四边形EBFD为平行四边形.证明:(2)∵四边形EBFD为平行四边形,
∴∠ABN=∠CDM.
∵AB∥CD,∴∠BAN=∠DCM.
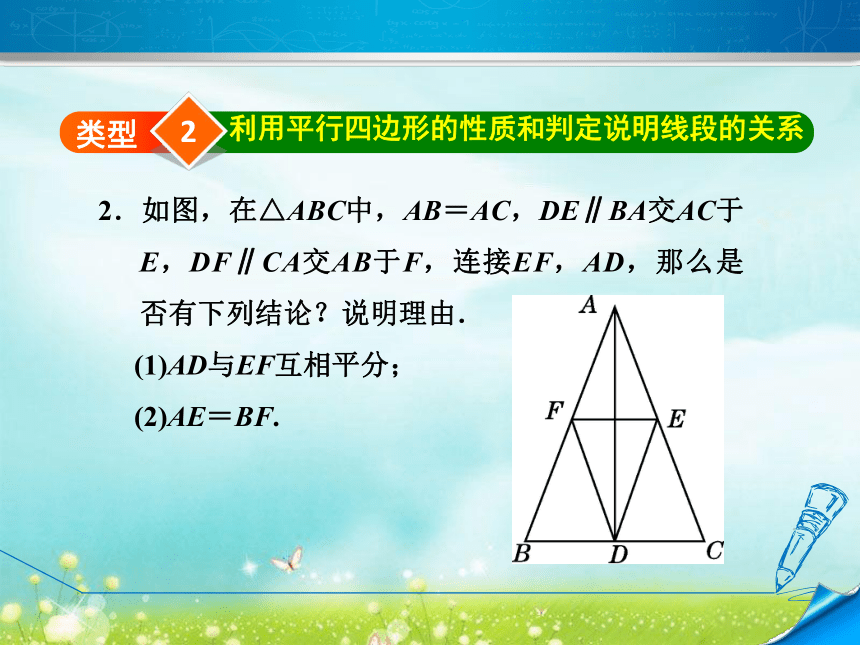
又∵AB=CD,∴△ABN≌△CDM.2利用平行四边形的性质和判定说明线段的关系类型2.如图,在△ABC中,AB=AC,DE∥BA交AC于E,DF∥CA交AB于F,连接EF,AD,那么是否有下列结论?说明理由.
(1)AD与EF互相平分;
(2)AE=BF.结论(1)(2)都成立,理由如下:
(1)∵DE∥AB,DF∥AC,
∴四边形AFDE是平行四边形.
∴AD与EF互相平分.
(2)在?AFDE中,AE=DF,
∵AC∥DF,
∴∠C=∠FDB.
∵AB=AC,∴∠C=∠B,
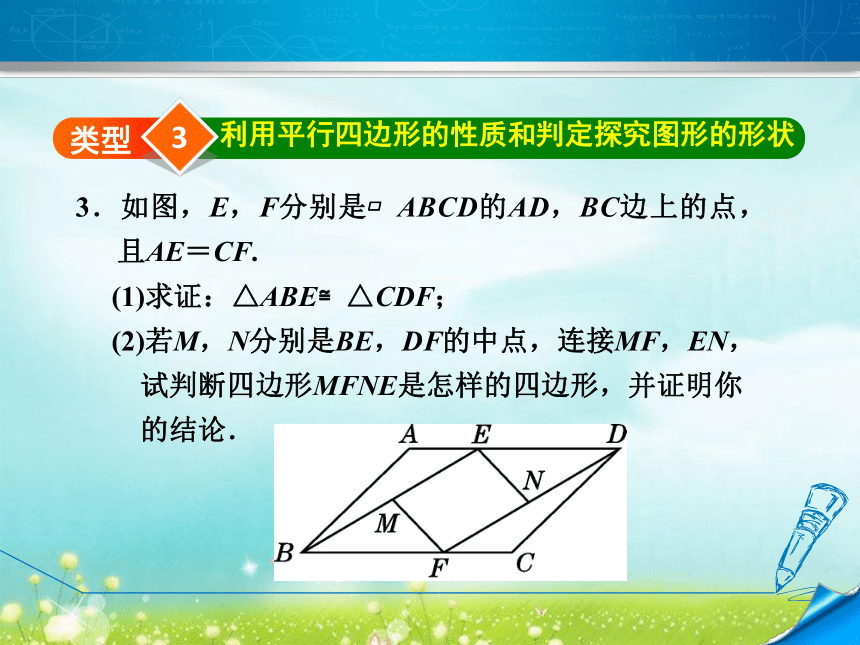
∴∠B=∠FDB,∴BF=DF=AE,即AE=BF.解: 3利用平行四边形的性质和判定探究图形的形状类型3.如图,E,F分别是?ABCD的AD,BC边上的点,且AE=CF.
(1)求证:△ABE≌△CDF;
(2)若M,N分别是BE,DF的中点,连接MF,EN,
试判断四边形MFNE是怎样的四边形,并证明你
的结论.(1)∵四边形ABCD是平行四边形,
∴AB=CD,∠A=∠C.
∵AE=CF,∴△ABE≌△CDF(SAS).
(2) 四边形MFNE是平行四边形.证明如下:
∵△ABE≌△CDF,
∴∠AEB=∠CFD,BE=DF.
又∵M,N分别是BE,DF的中点,
∴ME=FN.解: 证明:∵四边形ABCD是平行四边形,
∴BC∥AD,
∴∠AEB=∠FBE. ∴∠CFD=∠FBE.
∴EB∥DF,即ME∥FN.
∴四边形MFNE是平行四边形.
点拨:
本题是一道猜想型问题,先猜想结论,再证明
结论.本题已知一个四边形是平行四边形,借助其
性质,利用平行四边形的判定方法判定另一个四边
形是平行四边形.4利用平行四边形的性质证明线段间数量关系4.如图,将?ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,折痕l交CD边于点E,连接BE.
(1)求证:四边形BCED′是平行四边形;
(2)若BE平分∠ABC,求证:AB2=AE2+BE2.类型(1)∵将?ABCD沿过点A的直线l折叠,使点D落到
AB边上的点D′处,
∴∠DAE=∠D′AE,∠DEA=∠D′EA,
∠D=∠AD′E.
∵∠D=∠ABC,
∴∠AD′E=∠ABC. ∴ED′∥CB.
∵四边形ABCD是平行四边形,
∴EC∥D′B,
∴四边形BCED′是平行四边形.解:(2)∵BE平分∠ABC,
∴∠CBE=∠EBA.
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAB+∠CBA=180°.
∵∠DAE=∠BAE,
∴∠BAE+∠EBA=90°.
∴∠AEB=90°.
∴AB2=AE2+BE2.5利用平行四边形的判定和性质证平行5.如图所示,平行四边形ABCD的对角线AC,BD交于点O,E,F在AC上,G,H在BD上,AF=CE,BH=DG. GF与HE平行吗?请说明理由.类型GF∥HE.
理由:连结EG,HF.
在平行四边形ABCD中,OA=OC,
因为AF=CE,
所以AF-OA=CE-OC,
所以OF=OE.
同理得OG=OH.
所以四边形EGFH是平行四边形,
所以GF∥HE.解:6利用平行四边形的判定和性质求面积6.如图,Rt△AOB的直角边OA,OB分别在y轴、x
轴上,点A,B的坐标分别是(0,4),(3,0).将△AOB向右平移,当点A落在直线y=x-1上时,
线段AB扫过的面积是多少?类型如图,将△AOB向右平移,
当点A落在直线y=x-1上时,
线段AB扫过的图形是四边形
ABB′A′,由平移易证
四边形ABB′A′是平行四边形.
∵A(0,4),B(3,0),
∴A′点的纵坐标是4,将y=4代入y=x-1,得x=5,
∴A′(5,4),∴BB′=AA′=5,
∴平行四边形ABB′A′的面积是5×4=20.解:点拨:
根据平行四边形的定义可以知道线段AB扫过
的图形是平行四边形,求出A′点的坐标是解题的
关键.7利用平行四边形的性质和判定求线段的和(归一法)如图,等边三角形ABC的边长为7 cm,M为△ABC
内任意一点,MD∥AC,ME∥AB,MF∥BC,试
求MD+ME+MF的值.类型延长EM交AC于点G,延长DM交BC于点H.
∵MD∥AC,ME∥AB,MF∥BC,
∴四边形ADMG和四边形MHCF都是平行四边形,
∴MD=AG,MH=CF.
由△ABC是等边三角形,易证△MGF和△MEH都是等边三角形,
∴MF=GF,ME=MH=CF,
∴MD+ME+MF=AG+CF+GF=AC=7 cm.解:8利用平行四边形的性质和判定探究动点问题8.如图所示,在四边形ABCD中,AD∥BC,BC=18 cm,CD=15 cm,AD=10 cm,AB=12 cm,动点P、Q分别从点A、C同时出发,点P以2 cm/s的速度由A向D运动,点Q以3 cm/s的速度由C向B运动.
(1)几秒后,四边形ABQP为平行四边形?
并求出此时四边形ABQP的周长;
(2)几秒后,四边形PDCQ为平行四边形?
并求出此时四边形PDCQ的周长.类型(1)设x s后,四边形ABQP为平行四边形,
由题意易得2x=18-3x,解得x=3.6,
即3.6 s后,四边形ABQP为平行四边
形,此时四边形ABQP的周长是
3.6×2×2+12×2=38.4(cm).
(2)设y s后,四边形PDCQ为平行四边形.
由题意易得10-2y=3y,解得y=2,
即2 s后,四边形PDCQ为平行四边形,
此时四边形PDCQ的周长是3×2×2+15×2=42(cm).解:
(1)联系:平行四边形的性质的题设和结论正好与判定
的题设和结论相反,它们构成互逆的关系.
(2)区别:由平行四边形这一条件得到边、角或对角线
的关系,这是平行四边形的性质;反之,由边、角
或对角线的关系得到平行四边形,这是平行四边形
的判定.1类型利用平行四边形的性质和判定判定平行四边形1.如图,在?ABCD中,E,F分别是AB,
CD的中点.
(1)求证:四边形EBFD为平行四边形;
(2)对角线AC分别与DE,BF交于点M,N,求证:
△ABN≌△CDM.(1)∵四边形ABCD为平行四边形,
∴AB=CD,EB∥DF.
又∵E,F分别是AB,CD的中点,
∴EB= AB,DF= CD.
∴EB=DF.
∴四边形EBFD为平行四边形.证明:(2)∵四边形EBFD为平行四边形,
∴∠ABN=∠CDM.
∵AB∥CD,∴∠BAN=∠DCM.
又∵AB=CD,∴△ABN≌△CDM.2利用平行四边形的性质和判定说明线段的关系类型2.如图,在△ABC中,AB=AC,DE∥BA交AC于E,DF∥CA交AB于F,连接EF,AD,那么是否有下列结论?说明理由.
(1)AD与EF互相平分;
(2)AE=BF.结论(1)(2)都成立,理由如下:
(1)∵DE∥AB,DF∥AC,
∴四边形AFDE是平行四边形.
∴AD与EF互相平分.
(2)在?AFDE中,AE=DF,
∵AC∥DF,
∴∠C=∠FDB.
∵AB=AC,∴∠C=∠B,
∴∠B=∠FDB,∴BF=DF=AE,即AE=BF.解: 3利用平行四边形的性质和判定探究图形的形状类型3.如图,E,F分别是?ABCD的AD,BC边上的点,且AE=CF.
(1)求证:△ABE≌△CDF;
(2)若M,N分别是BE,DF的中点,连接MF,EN,
试判断四边形MFNE是怎样的四边形,并证明你
的结论.(1)∵四边形ABCD是平行四边形,
∴AB=CD,∠A=∠C.
∵AE=CF,∴△ABE≌△CDF(SAS).
(2) 四边形MFNE是平行四边形.证明如下:
∵△ABE≌△CDF,
∴∠AEB=∠CFD,BE=DF.
又∵M,N分别是BE,DF的中点,
∴ME=FN.解: 证明:∵四边形ABCD是平行四边形,
∴BC∥AD,
∴∠AEB=∠FBE. ∴∠CFD=∠FBE.
∴EB∥DF,即ME∥FN.
∴四边形MFNE是平行四边形.
点拨:
本题是一道猜想型问题,先猜想结论,再证明
结论.本题已知一个四边形是平行四边形,借助其
性质,利用平行四边形的判定方法判定另一个四边
形是平行四边形.4利用平行四边形的性质证明线段间数量关系4.如图,将?ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,折痕l交CD边于点E,连接BE.
(1)求证:四边形BCED′是平行四边形;
(2)若BE平分∠ABC,求证:AB2=AE2+BE2.类型(1)∵将?ABCD沿过点A的直线l折叠,使点D落到
AB边上的点D′处,
∴∠DAE=∠D′AE,∠DEA=∠D′EA,
∠D=∠AD′E.
∵∠D=∠ABC,
∴∠AD′E=∠ABC. ∴ED′∥CB.
∵四边形ABCD是平行四边形,
∴EC∥D′B,
∴四边形BCED′是平行四边形.解:(2)∵BE平分∠ABC,
∴∠CBE=∠EBA.
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAB+∠CBA=180°.
∵∠DAE=∠BAE,
∴∠BAE+∠EBA=90°.
∴∠AEB=90°.
∴AB2=AE2+BE2.5利用平行四边形的判定和性质证平行5.如图所示,平行四边形ABCD的对角线AC,BD交于点O,E,F在AC上,G,H在BD上,AF=CE,BH=DG. GF与HE平行吗?请说明理由.类型GF∥HE.
理由:连结EG,HF.
在平行四边形ABCD中,OA=OC,
因为AF=CE,
所以AF-OA=CE-OC,
所以OF=OE.
同理得OG=OH.
所以四边形EGFH是平行四边形,
所以GF∥HE.解:6利用平行四边形的判定和性质求面积6.如图,Rt△AOB的直角边OA,OB分别在y轴、x
轴上,点A,B的坐标分别是(0,4),(3,0).将△AOB向右平移,当点A落在直线y=x-1上时,
线段AB扫过的面积是多少?类型如图,将△AOB向右平移,
当点A落在直线y=x-1上时,
线段AB扫过的图形是四边形
ABB′A′,由平移易证
四边形ABB′A′是平行四边形.
∵A(0,4),B(3,0),
∴A′点的纵坐标是4,将y=4代入y=x-1,得x=5,
∴A′(5,4),∴BB′=AA′=5,
∴平行四边形ABB′A′的面积是5×4=20.解:点拨:
根据平行四边形的定义可以知道线段AB扫过
的图形是平行四边形,求出A′点的坐标是解题的
关键.7利用平行四边形的性质和判定求线段的和(归一法)如图,等边三角形ABC的边长为7 cm,M为△ABC
内任意一点,MD∥AC,ME∥AB,MF∥BC,试
求MD+ME+MF的值.类型延长EM交AC于点G,延长DM交BC于点H.
∵MD∥AC,ME∥AB,MF∥BC,
∴四边形ADMG和四边形MHCF都是平行四边形,
∴MD=AG,MH=CF.
由△ABC是等边三角形,易证△MGF和△MEH都是等边三角形,
∴MF=GF,ME=MH=CF,
∴MD+ME+MF=AG+CF+GF=AC=7 cm.解:8利用平行四边形的性质和判定探究动点问题8.如图所示,在四边形ABCD中,AD∥BC,BC=18 cm,CD=15 cm,AD=10 cm,AB=12 cm,动点P、Q分别从点A、C同时出发,点P以2 cm/s的速度由A向D运动,点Q以3 cm/s的速度由C向B运动.
(1)几秒后,四边形ABQP为平行四边形?
并求出此时四边形ABQP的周长;
(2)几秒后,四边形PDCQ为平行四边形?
并求出此时四边形PDCQ的周长.类型(1)设x s后,四边形ABQP为平行四边形,
由题意易得2x=18-3x,解得x=3.6,
即3.6 s后,四边形ABQP为平行四边
形,此时四边形ABQP的周长是
3.6×2×2+12×2=38.4(cm).
(2)设y s后,四边形PDCQ为平行四边形.
由题意易得10-2y=3y,解得y=2,
即2 s后,四边形PDCQ为平行四边形,
此时四边形PDCQ的周长是3×2×2+15×2=42(cm).解:
