19.1.2 矩形的判定 课件
图片预览











文档简介
课件31张PPT。19.1.2 矩形的判定1课堂讲解由直角的个数判定矩形
由对角线的关系判定矩形2课时流程逐点
导讲练课堂小结作业提升 我们已经知道,有一个角是直角的平行四边形是
矩形,这是矩形的定义,我们可以依此判定一个四边
形是否是矩形. 除此之外,我们能否找到其他判定矩
形的方法呢?
矩形是特殊的平行四边形,具有如下性质:
1.四个角都是直角;
2.两条对角线相等.
这些性质,对我们寻找判定矩形的方法有什么启示?1知识点由直角的个数判定矩形知1-讲矩形的判定:
方法一(定义判定):有一个角是直角的平行四边形
是矩形;
方法二(角判定):有三个角是直角的四边形是矩形;知1-讲易错警示:
用定义判定一个四边形是矩形必须满足两个条件:
一是有一个角是直角,二是四边形是平行四边形.
也就是说有一个角是直角的四边形不一定是矩形,
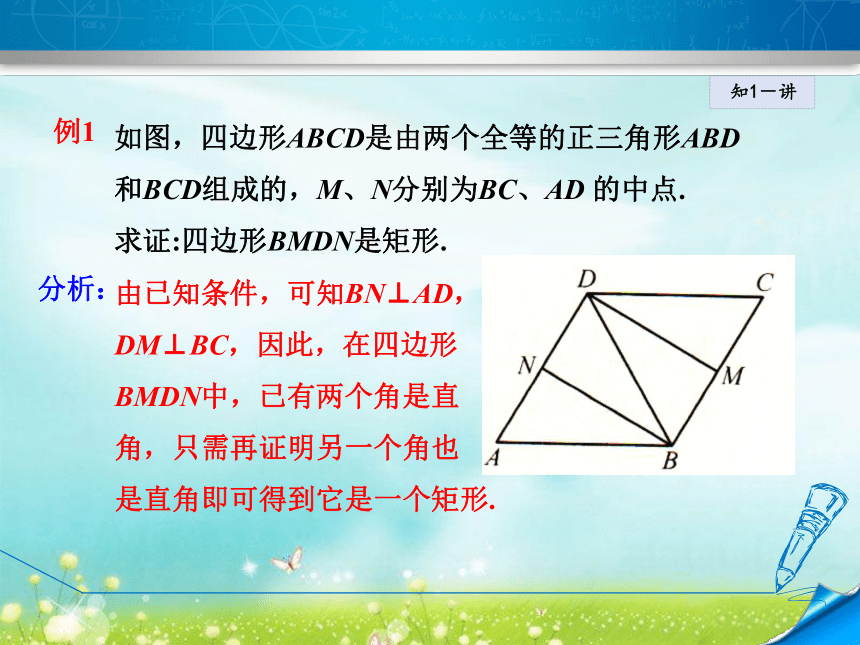
必须加上“平行四边形”这个条件它才是矩形.知1-讲例1 如图,四边形ABCD是由两个全等的正三角形ABD和BCD组成的,M、N分别为BC、AD 的中点.
求证:四边形BMDN是矩形.分析:由已知条件,可知BN⊥AD,
DM⊥BC,因此,在四边形
BMDN中,已有两个角是直
角,只需再证明另一个角也
是直角即可得到它是一个矩形.知1-讲证明:∵△ABD和△BCD是全等的正三角形,
∴∠ADB=∠CDB=60°.
又∵M、N分别为BC、AD的中点,
∴BN⊥AD,DM⊥BC,∠BDM=30°,
∴∠DNB=∠DMB=90°,
∠MDN=∠ADB+∠BDM=90°,
∴四边形BMDN是矩形(有三个角是直角的四边形
是矩形).知1-讲例2 如图, ABCD的四个内角的平分线分别相交于点
E,F,G,H. 求证:四边形EFGH是矩形.导引:要证明四边形EFGH是矩形,
由于已知ABCD的四个内角的
平分线分别相交于点E,F,
G,H,因此可选用“有三个
角是直角的四边形是矩形”
来证明.知1-讲∵AB∥CD,∴∠ABC+∠BCD=180°.
∵BG平分∠ABC,CG平分∠BCD,
∴∠GBC+∠GCB= ×180°=90°,
∴∠BGC=90°.
同理可得∠AFB=∠AED=90°.
∴∠GFE=∠FEH=∠FGH=90°.
∴四边形EFGH是矩形.证明: 本题目中的图形是建立在平行四边形基础上,
而条件中又涉及角的关系,一般采用“角的方法”
来判定矩形.知1-讲1 如图,AB、CD是⊙O的两条直径,四边形ACBD是矩形吗?证明你的结论.知1-练2 在 ABCD中,增加下列条件中的一个,就能判定
它是矩形的是( )
A.∠A+∠C=180°
B.AB=BC
C.AC⊥BD
D.AC=2AB知1-练3 数学课上,老师要同学们判断一个四边形门框是否为矩形.下面是某合作小组的4位同学给出的方案,其中正确的是( )
A.测量对角线是否互相平分
B.测量两组对边是否分别相等
C.测量一组对角是否都为直角
D.测量三个角是否都为直角知1-练2知识点由对角线的关系判定矩形知2-讲矩形的判定:
方法三(对角线判定):对角线相等的平行四边形是矩
形;或对角线相等且互相平分的四边形是矩形.
要点精析:(1)矩形的判定与性质是互逆定理;
(2)判定矩形的
常见思路如
图:知2-讲易错警示:
用对角线相等的平行四边形是矩形判定一个四边
形是矩形必须满足两个条件:一是对角线相等,
二是四边形是平行四边形.也就是说两条对角线
相等的四边形不一定是矩形,必须加上“平行四
边形”这个条件它才是矩形.知2-讲例3 如图,点O是矩形ABCD的对角线AC与BD的交点,E、F、G、H分别是AO、BO、CO、DO上的一点,且AE=BF=CG=DH.求证:四边形EFGH是矩形.根据已知条件,我们可以
先证明四边形EFGH是平
行四边形,再证明对角线
EG和FH相等,即可得证.分析:知2-讲∵四边形ABCD是矩形,
∴AO=BO=CO=DO.
∵AE=BF=CG=DH,
∴OE=OF=OG=OH,
∴四边形EFGH是平行四边形.
∵EO+OG=FO+OH,
即EG=FH,
∴四边形EFGH是矩形(对角线相等的平行四
边形是矩形).证明:知2-讲例4 如图,在△ABC中,AB=AC,AD⊥BC,垂足为点
D,AG是△ABC的外角∠FAC的平分线,DE∥AB,
交AG于点E. 求证:四边形ADCE是矩形.根据已知条件AB=AC ,我们
可以先通过证明四边形ABDE
是平行四边形,得到DE=AB
=AC,因此可以利用“对角线
相等的平行四边形是矩形”这
一判定定理.分析:知2-讲∵ AB=AC,AD⊥BC,
∴∠B=∠ACB,BD=DC.
又∵AE是△ABC的外角∠CAF的平分线,
∴∠1= ∠CAF= (∠B+∠ACB) =∠B,
∴AE∥BC.
又∵AB∥DE,∴四边形ABDE是平行四边形,
∴AE=BD,AB=DE,∴AC=DE,AE=DC.
又∵AE∥DC,∴四边形ADCE是平行四边形,
∴四边形ADCE是矩形(对角线相等的平行四边
形是矩形).?证明:知2-讲例5 〈探究题〉如图,在矩形ABCD中,AB=2,BC=5,E、P分别在AD、BC上,且DE=BP=1,AP,BE相交于点H,CE,DP相交于点F.
(1)判断△BEC的形状,并说明理由;
(2)判断四边形EFPH是什么特殊四边形,并证明你
的判断.知2-讲根据矩形性质得出CD=2,AD=5,根据勾股定
理求出CE和BE,进而求出CE2+BE2,BC2,根
据勾股定理的逆定理即可判断△BEC的形状;导引:(1)判断△BEC的形状,并说明理由;知2-讲(1)△BEC是直角三角形.
理由:∵四边形ABCD是矩形,
∴∠ADC=∠EAB=90°,AD=BC=5,
CD=AB=2,
由勾股定理得:CE=
同理BE= ,∴CE2+BE2=5+20=25.
∵BC2=52=25,∴BE2+CE2=BC2,
∴∠BEC=90°,
∴△BEC是直角三角形.解:知2-讲根据矩形的性质和平行四
边形的判定,推出四边形
DEBP和四边形AECP均为
平行四边形,进而推出四边形EFPH为平行四边
形,根据矩形的判定即可得出结论.导引:(2)判断四边形EFPH是什么特殊四边形,并证明你
的判断.知2-讲(2)四边形EFPH为矩形.
∵四边形ABCD是矩形,∴AD=BC,AD∥BC.
∵DE=BP,DE∥BP,
∴四边形DEBP是平行四边形,∴BE∥DP.
∵AD=BC,AD∥BC,DE=BP,
∴AE=CP,AE∥CP,
∴四边形AECP是平行四边形,
∴AP∥CE,∴四边形EFPH是平行四边形.
∵∠BEC=90°,∴平行四边形EFPH是矩形.解:证明: 本题综合考查了勾股定理及其逆定理,矩形、
平行四边形的性质和判定等知识,主要培养学生分
析问题和解决问题的能力.知2-讲1 如图,将 ABCD的边DC延长到点E使CE=DC,连
结AE,交BC于点F,∠AFC=2∠D,连结AC、BE.求证:四边形ABEC是矩形.知2-练知2-练2 下列四边形:
①对角线互相平分的四边形;
②对角线相等的四边形;
③对角线相等的平行四边形;
④对角线互相平分且相等的四边形.
其中一定是矩形的个数是( )
A.1个 B.2个 C.3个 D.4个知2-练3 在 ABCD中,对角线AC,BD相交于点O,再添加一个条件,仍不能判定四边形ABCD是矩形的是( )
A.AB=AD B.OA=OB
C.AC=BD D.DC⊥BC知2-练4 对于四边形ABCD,给出下列6组条件:
①∠A=90°,∠B=∠C=∠D;
②∠A=∠B=90°,∠C=∠D;
③∠A=∠B=∠C=∠D;
④∠A=∠B=∠C=90°;
⑤AC=BD;
⑥AB∥CD,AD∥BC.
其中能得到“四边形ABCD是矩形”的有( )
A.1组 B.2组 C.3组 D.4组判定定理1平行四边形的判定有一个角是直角(定义)对角线互相平分且相等判定定理2(有三个角是直角)(对角线相等)1.必做: 完成教材P104练习T2-3,
P106练习T1-2
2.补充: 请完成练习册剩余部分习题
由对角线的关系判定矩形2课时流程逐点
导讲练课堂小结作业提升 我们已经知道,有一个角是直角的平行四边形是
矩形,这是矩形的定义,我们可以依此判定一个四边
形是否是矩形. 除此之外,我们能否找到其他判定矩
形的方法呢?
矩形是特殊的平行四边形,具有如下性质:
1.四个角都是直角;
2.两条对角线相等.
这些性质,对我们寻找判定矩形的方法有什么启示?1知识点由直角的个数判定矩形知1-讲矩形的判定:
方法一(定义判定):有一个角是直角的平行四边形
是矩形;
方法二(角判定):有三个角是直角的四边形是矩形;知1-讲易错警示:
用定义判定一个四边形是矩形必须满足两个条件:
一是有一个角是直角,二是四边形是平行四边形.
也就是说有一个角是直角的四边形不一定是矩形,
必须加上“平行四边形”这个条件它才是矩形.知1-讲例1 如图,四边形ABCD是由两个全等的正三角形ABD和BCD组成的,M、N分别为BC、AD 的中点.
求证:四边形BMDN是矩形.分析:由已知条件,可知BN⊥AD,
DM⊥BC,因此,在四边形
BMDN中,已有两个角是直
角,只需再证明另一个角也
是直角即可得到它是一个矩形.知1-讲证明:∵△ABD和△BCD是全等的正三角形,
∴∠ADB=∠CDB=60°.
又∵M、N分别为BC、AD的中点,
∴BN⊥AD,DM⊥BC,∠BDM=30°,
∴∠DNB=∠DMB=90°,
∠MDN=∠ADB+∠BDM=90°,
∴四边形BMDN是矩形(有三个角是直角的四边形
是矩形).知1-讲例2 如图, ABCD的四个内角的平分线分别相交于点
E,F,G,H. 求证:四边形EFGH是矩形.导引:要证明四边形EFGH是矩形,
由于已知ABCD的四个内角的
平分线分别相交于点E,F,
G,H,因此可选用“有三个
角是直角的四边形是矩形”
来证明.知1-讲∵AB∥CD,∴∠ABC+∠BCD=180°.
∵BG平分∠ABC,CG平分∠BCD,
∴∠GBC+∠GCB= ×180°=90°,
∴∠BGC=90°.
同理可得∠AFB=∠AED=90°.
∴∠GFE=∠FEH=∠FGH=90°.
∴四边形EFGH是矩形.证明: 本题目中的图形是建立在平行四边形基础上,
而条件中又涉及角的关系,一般采用“角的方法”
来判定矩形.知1-讲1 如图,AB、CD是⊙O的两条直径,四边形ACBD是矩形吗?证明你的结论.知1-练2 在 ABCD中,增加下列条件中的一个,就能判定
它是矩形的是( )
A.∠A+∠C=180°
B.AB=BC
C.AC⊥BD
D.AC=2AB知1-练3 数学课上,老师要同学们判断一个四边形门框是否为矩形.下面是某合作小组的4位同学给出的方案,其中正确的是( )
A.测量对角线是否互相平分
B.测量两组对边是否分别相等
C.测量一组对角是否都为直角
D.测量三个角是否都为直角知1-练2知识点由对角线的关系判定矩形知2-讲矩形的判定:
方法三(对角线判定):对角线相等的平行四边形是矩
形;或对角线相等且互相平分的四边形是矩形.
要点精析:(1)矩形的判定与性质是互逆定理;
(2)判定矩形的
常见思路如
图:知2-讲易错警示:
用对角线相等的平行四边形是矩形判定一个四边
形是矩形必须满足两个条件:一是对角线相等,
二是四边形是平行四边形.也就是说两条对角线
相等的四边形不一定是矩形,必须加上“平行四
边形”这个条件它才是矩形.知2-讲例3 如图,点O是矩形ABCD的对角线AC与BD的交点,E、F、G、H分别是AO、BO、CO、DO上的一点,且AE=BF=CG=DH.求证:四边形EFGH是矩形.根据已知条件,我们可以
先证明四边形EFGH是平
行四边形,再证明对角线
EG和FH相等,即可得证.分析:知2-讲∵四边形ABCD是矩形,
∴AO=BO=CO=DO.
∵AE=BF=CG=DH,
∴OE=OF=OG=OH,
∴四边形EFGH是平行四边形.
∵EO+OG=FO+OH,
即EG=FH,
∴四边形EFGH是矩形(对角线相等的平行四
边形是矩形).证明:知2-讲例4 如图,在△ABC中,AB=AC,AD⊥BC,垂足为点
D,AG是△ABC的外角∠FAC的平分线,DE∥AB,
交AG于点E. 求证:四边形ADCE是矩形.根据已知条件AB=AC ,我们
可以先通过证明四边形ABDE
是平行四边形,得到DE=AB
=AC,因此可以利用“对角线
相等的平行四边形是矩形”这
一判定定理.分析:知2-讲∵ AB=AC,AD⊥BC,
∴∠B=∠ACB,BD=DC.
又∵AE是△ABC的外角∠CAF的平分线,
∴∠1= ∠CAF= (∠B+∠ACB) =∠B,
∴AE∥BC.
又∵AB∥DE,∴四边形ABDE是平行四边形,
∴AE=BD,AB=DE,∴AC=DE,AE=DC.
又∵AE∥DC,∴四边形ADCE是平行四边形,
∴四边形ADCE是矩形(对角线相等的平行四边
形是矩形).?证明:知2-讲例5 〈探究题〉如图,在矩形ABCD中,AB=2,BC=5,E、P分别在AD、BC上,且DE=BP=1,AP,BE相交于点H,CE,DP相交于点F.
(1)判断△BEC的形状,并说明理由;
(2)判断四边形EFPH是什么特殊四边形,并证明你
的判断.知2-讲根据矩形性质得出CD=2,AD=5,根据勾股定
理求出CE和BE,进而求出CE2+BE2,BC2,根
据勾股定理的逆定理即可判断△BEC的形状;导引:(1)判断△BEC的形状,并说明理由;知2-讲(1)△BEC是直角三角形.
理由:∵四边形ABCD是矩形,
∴∠ADC=∠EAB=90°,AD=BC=5,
CD=AB=2,
由勾股定理得:CE=
同理BE= ,∴CE2+BE2=5+20=25.
∵BC2=52=25,∴BE2+CE2=BC2,
∴∠BEC=90°,
∴△BEC是直角三角形.解:知2-讲根据矩形的性质和平行四
边形的判定,推出四边形
DEBP和四边形AECP均为
平行四边形,进而推出四边形EFPH为平行四边
形,根据矩形的判定即可得出结论.导引:(2)判断四边形EFPH是什么特殊四边形,并证明你
的判断.知2-讲(2)四边形EFPH为矩形.
∵四边形ABCD是矩形,∴AD=BC,AD∥BC.
∵DE=BP,DE∥BP,
∴四边形DEBP是平行四边形,∴BE∥DP.
∵AD=BC,AD∥BC,DE=BP,
∴AE=CP,AE∥CP,
∴四边形AECP是平行四边形,
∴AP∥CE,∴四边形EFPH是平行四边形.
∵∠BEC=90°,∴平行四边形EFPH是矩形.解:证明: 本题综合考查了勾股定理及其逆定理,矩形、
平行四边形的性质和判定等知识,主要培养学生分
析问题和解决问题的能力.知2-讲1 如图,将 ABCD的边DC延长到点E使CE=DC,连
结AE,交BC于点F,∠AFC=2∠D,连结AC、BE.求证:四边形ABEC是矩形.知2-练知2-练2 下列四边形:
①对角线互相平分的四边形;
②对角线相等的四边形;
③对角线相等的平行四边形;
④对角线互相平分且相等的四边形.
其中一定是矩形的个数是( )
A.1个 B.2个 C.3个 D.4个知2-练3 在 ABCD中,对角线AC,BD相交于点O,再添加一个条件,仍不能判定四边形ABCD是矩形的是( )
A.AB=AD B.OA=OB
C.AC=BD D.DC⊥BC知2-练4 对于四边形ABCD,给出下列6组条件:
①∠A=90°,∠B=∠C=∠D;
②∠A=∠B=90°,∠C=∠D;
③∠A=∠B=∠C=∠D;
④∠A=∠B=∠C=90°;
⑤AC=BD;
⑥AB∥CD,AD∥BC.
其中能得到“四边形ABCD是矩形”的有( )
A.1组 B.2组 C.3组 D.4组判定定理1平行四边形的判定有一个角是直角(定义)对角线互相平分且相等判定定理2(有三个角是直角)(对角线相等)1.必做: 完成教材P104练习T2-3,
P106练习T1-2
2.补充: 请完成练习册剩余部分习题
