19.2.1 菱形及其性质 课件
图片预览








文档简介
课件30张PPT。19.2.1 菱形及其性质1课堂讲解菱形的定义
菱形的对称性
菱形的边的性质
菱形的对角线的性质2课时流程逐点
导讲练课堂小结作业提升什么是矩形?
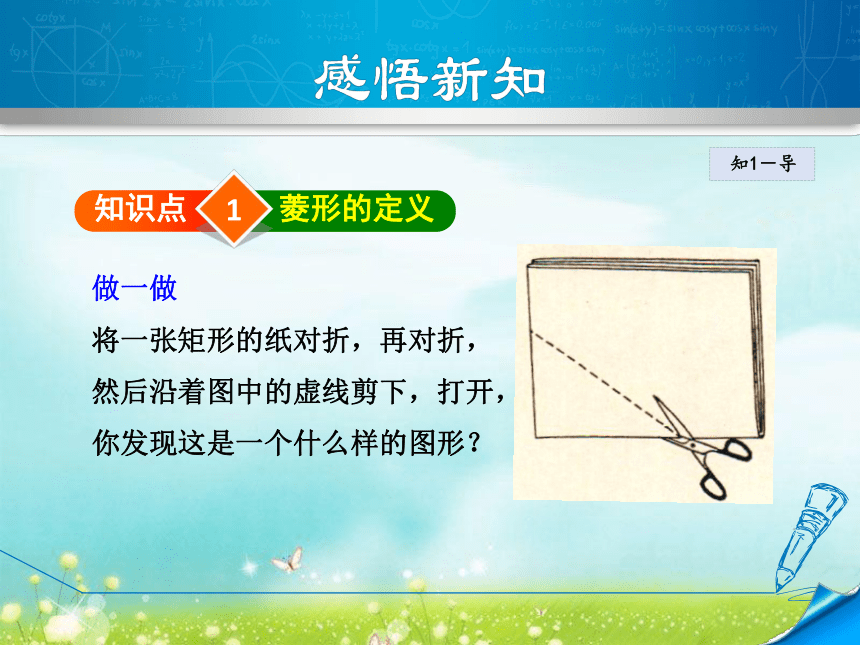
矩形都有哪些性质?1知识点菱形的定义知1-导做一做
将一张矩形的纸对折,再对折,
然后沿着图中的虚线剪下,打开,
你发现这是一个什么样的图形?知1-讲定义:有一组邻边相等的平行四边形叫做菱形.
要点精析:
(1)菱形必须满足两个条件:一是平行四边形; 二是
一组邻边相等.二者必须同时具备,缺一不可;
(2)菱形的定义既是菱形的基本性质,也是菱形的基
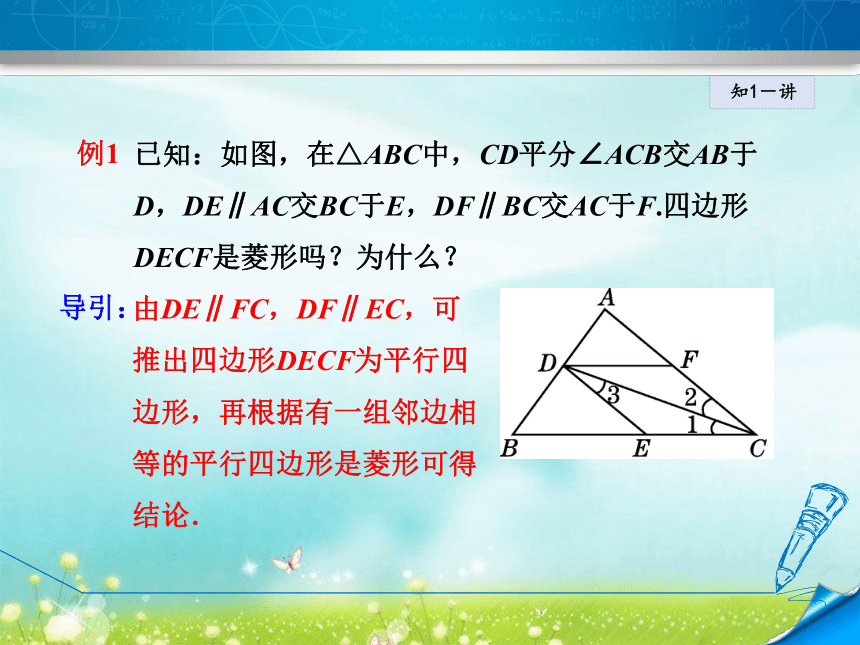
本判定方法.知1-讲例1 已知:如图,在△ABC中,CD平分∠ACB交AB于D,DE∥AC交BC于E,DF∥BC交AC于F.四边形DECF是菱形吗?为什么?导引:由DE∥FC,DF∥EC,可
推出四边形DECF为平行四
边形,再根据有一组邻边相
等的平行四边形是菱形可得
结论.知1-讲四边形DECF是菱形.
理由如下:
∵DE∥FC,DF∥EC,
∴四边形DECF为平行四边形.
由AC∥DE,知∠2=∠3.
∵CD平分∠ACB,
∴∠1=∠2,∴∠1=∠3,∴DE=EC,
∴平行四边形DECF为菱形(有一组邻边相等的平
行四边形是菱形).解: 本题考查了菱形的定义,菱形的定义也可以作
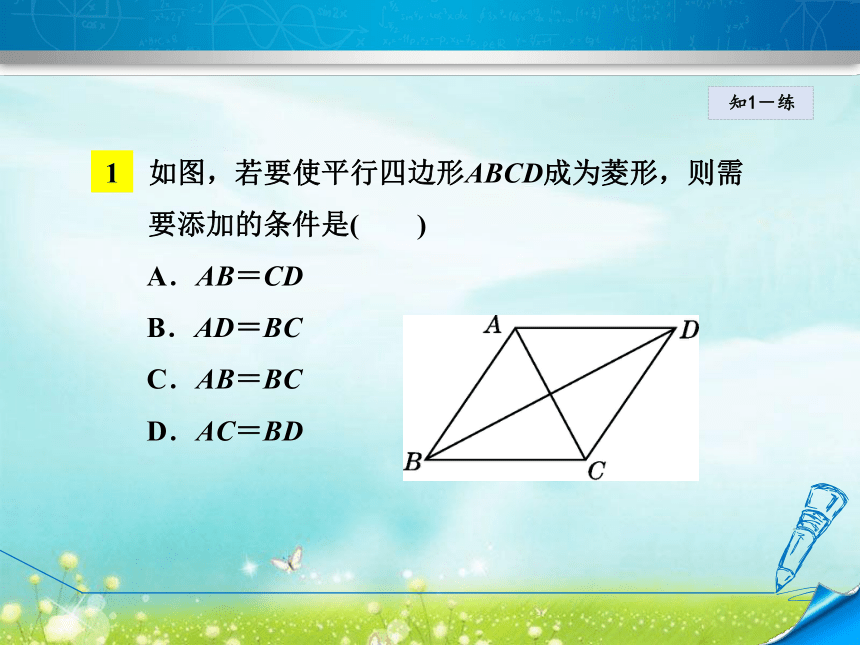
为菱形的判定方法.知1-讲1 如图,若要使平行四边形ABCD成为菱形,则需
要添加的条件是( )
A.AB=CD
B.AD=BC
C.AB=BC
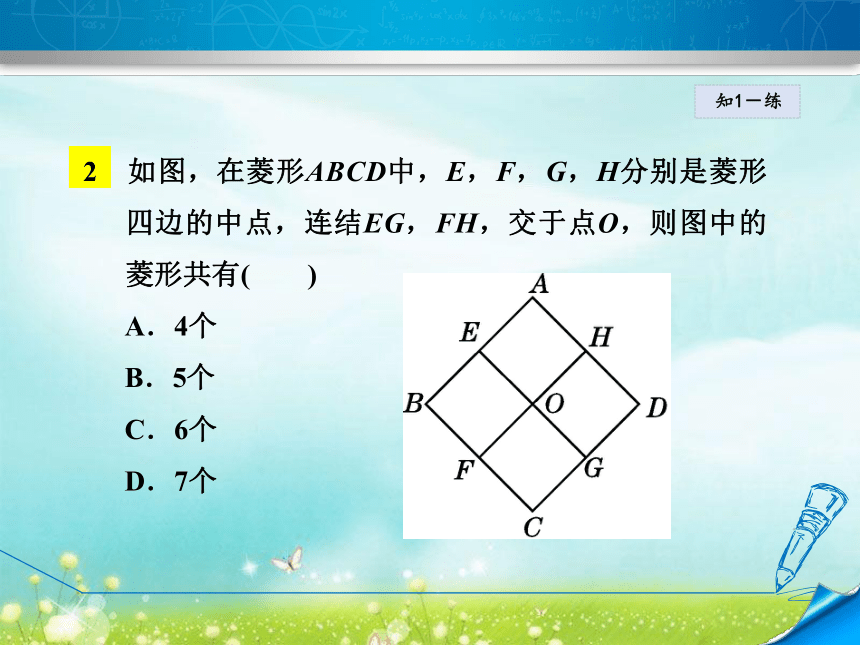
D.AC=BD知1-练2 如图,在菱形ABCD中,E,F,G,H分别是菱形四边的中点,连结EG,FH,交于点O,则图中的菱形共有( )
A.4个
B.5个
C.6个
D.7个知1-练2知识点菱形的对称性知2-导菱形有几条对称轴?对称中心在哪里?知2-讲 如图,我们发现,菱形既是中
心对称图形,也是轴对称图形,
对称轴为它的对角线所在的直线. 1 如图,O是菱形ABCD的对角线AC,BD的交点,E,F分别是OA,OC的中点,下列结论:
①S△ADE=S△EOD;
②四边形BFDE是中心对称图形;
③△DEF是轴对称图形;
④∠ADE=∠EDO.
其中正确的有( )
A.1个 B.2个 C.3个 D.4个知2-练知2-练2 如图,在菱形ABCD中,点A在x轴上,点B的坐标为(8,2),点D的坐标为(0,2),则点C
的坐标为________.3知识点菱形的边的性质知3-讲菱形的性质1 菱形的四条边都相等.例2 如图,在菱形ABCD中,∠BAD=2∠B. 试求出∠B的大小,并说明△ABC是等边三角形.解:在菱形ABCD中,
∵∠B+∠BAD=180°,
∠BAD=2∠B,
∴∠B=60°.
在菱形ABCD中,
∵AB=BC(菱形的四条边都相等),∠B=60°,
∴△ABC是等边三角形.知3-讲例3 如图,菱形ABCD的对角线AC与BD 相交于点O,AE垂直且平分CD,垂足为点E. 求∠BCD的大小.解:∵四边形ABCD是菱形,
∴AD=DC=CB=BA(菱形的
四条边都相等).
又∵AE垂直平分CD,
∴AC=AD,
∴AC=AD=DC=CB=BA,
即△ADC与△ABC都为等边三角形,
∴∠ACD=∠ACB=60°.
∴∠BCD=120°.知3-讲1 边长为3 cm的菱形的周长是( )
A.6 cm B.9 cm
C.12 cm D.15 cm
2 如图,在菱形ABCD中,AB=5,∠BCD=120°,则△ABC的周长等于( )
A.20
B.15
C.10
D.5知3-练4知识点菱形的对角线的性质知4-讲1.性质
(1)菱形的两条对角线互相垂直;
(2)菱形的每一条对角线平分一组对角;
(3)菱形具有平行四边形的一切性质;
2.菱形的面积计算:
①菱形的面积等于底乘高.
②菱形的面积等于对角线乘积的一半,对于对角线互相
垂直的四边形的面积都可以用两条对角线乘积的一半来
进行计算.3. 易错警示:
(1)菱形和矩形都是建立在平行四边形的基础上;
矩形是附加一直角;而菱形附加一组邻边相等;
(2)矩形的两条对角线把矩形分割成四个面积相等的
等腰三角形.而菱形的两条对角线把菱形分割成
四个全等的直角三角形;
(3)菱形的对称轴是两条对角线所在的直线,不要误
认为两条对角线是它的对称轴.知4-讲例4 如图,已知菱形ABCD的边长为 2 cm,∠BAD=120°,对角线AC、BD相交于点O. 试求这 个菱
形的两条对角线AC与BD的长. (结果保留根号)知4-讲解:∵四边形ABCD是菱形,
∴OB=OD,AB=AD(菱形的四条边都相等).
在△ABO和△ADO中,
∵AB=AD,AO=AO, OB=OD,
∴△ABO≌△ADO,
∴∠BAO=∠DAO = ∠BAD=60°.
在△ABC中,∵AB=BC,∠BAC=60°,
∴△ABC为等边三角形,∴AC=AB=2.知4-讲在菱形ABCD中,
∵AC⊥BD(菱形的对角线互相垂直),
∴△AOB为直角三角形,
∴
∴知4-讲例5 如图,在菱形ABCD中,对角线AC与BD相交于
点O,BD=6 cm,AC=4 cm. 求菱形的周长.知4-讲导引:由于菱形的四条边都相等,
所以要求其周长就要先求
出其边长.由菱形的性质
可知,其对角线互相垂直
平分,因此可以在直角三
角形中利用勾股定理来进
行计算.解:∵四边形ABCD是菱形,
∴AC⊥BD,AO= AC,BO= BD.
∵AC=4 cm,BD=6 cm,
∴AO=2 cm,BO=3 cm.
在Rt△ABO中,由勾股定理,得
∴菱形的周长=4AB= 知4-讲 菱形的对角线将菱形分成四个全等的直角三角
形,我们通常将菱形问题中求相关线段的长转化为
求直角三角形问题中相关线段的长,再利用勾股定
理来计算.知4-讲1 如图,在菱形ABCD中,AB=5,OA=4.求菱形
的周长与两条对角线的长度.
2 试说明菱形的面积等于它的
两条对角线长的乘积的一半.知4-练3 菱形具有而一般平行四边形不具有的
性质是( )
A.对边相等 B.对角相等
C.对角线互相平分 D.对角线互相垂直
4 如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH等于( )
A. B. C.5 D.4知4-练1.菱形具有平行四边形的一切性质.
2.菱形的每一条对角线平分一组对角.
3.菱形面积等于两对角线的长度乘积的一半.
4.菱形是中心对称图形,对称中心是两条对角线的交
点,菱形也是轴对称图形.
5.利用菱形的对角线计算线段的长度时,通常要借助
勾股定理来进行.
注意:菱形的对角线互相垂直平分,但不一定相等.1. 必做: 完成教材P112练习T3,
P113练习T1-3
2. 补充: 请完成练习册剩余部分习题
菱形的对称性
菱形的边的性质
菱形的对角线的性质2课时流程逐点
导讲练课堂小结作业提升什么是矩形?
矩形都有哪些性质?1知识点菱形的定义知1-导做一做
将一张矩形的纸对折,再对折,
然后沿着图中的虚线剪下,打开,
你发现这是一个什么样的图形?知1-讲定义:有一组邻边相等的平行四边形叫做菱形.
要点精析:
(1)菱形必须满足两个条件:一是平行四边形; 二是
一组邻边相等.二者必须同时具备,缺一不可;
(2)菱形的定义既是菱形的基本性质,也是菱形的基
本判定方法.知1-讲例1 已知:如图,在△ABC中,CD平分∠ACB交AB于D,DE∥AC交BC于E,DF∥BC交AC于F.四边形DECF是菱形吗?为什么?导引:由DE∥FC,DF∥EC,可
推出四边形DECF为平行四
边形,再根据有一组邻边相
等的平行四边形是菱形可得
结论.知1-讲四边形DECF是菱形.
理由如下:
∵DE∥FC,DF∥EC,
∴四边形DECF为平行四边形.
由AC∥DE,知∠2=∠3.
∵CD平分∠ACB,
∴∠1=∠2,∴∠1=∠3,∴DE=EC,
∴平行四边形DECF为菱形(有一组邻边相等的平
行四边形是菱形).解: 本题考查了菱形的定义,菱形的定义也可以作
为菱形的判定方法.知1-讲1 如图,若要使平行四边形ABCD成为菱形,则需
要添加的条件是( )
A.AB=CD
B.AD=BC
C.AB=BC
D.AC=BD知1-练2 如图,在菱形ABCD中,E,F,G,H分别是菱形四边的中点,连结EG,FH,交于点O,则图中的菱形共有( )
A.4个
B.5个
C.6个
D.7个知1-练2知识点菱形的对称性知2-导菱形有几条对称轴?对称中心在哪里?知2-讲 如图,我们发现,菱形既是中
心对称图形,也是轴对称图形,
对称轴为它的对角线所在的直线. 1 如图,O是菱形ABCD的对角线AC,BD的交点,E,F分别是OA,OC的中点,下列结论:
①S△ADE=S△EOD;
②四边形BFDE是中心对称图形;
③△DEF是轴对称图形;
④∠ADE=∠EDO.
其中正确的有( )
A.1个 B.2个 C.3个 D.4个知2-练知2-练2 如图,在菱形ABCD中,点A在x轴上,点B的坐标为(8,2),点D的坐标为(0,2),则点C
的坐标为________.3知识点菱形的边的性质知3-讲菱形的性质1 菱形的四条边都相等.例2 如图,在菱形ABCD中,∠BAD=2∠B. 试求出∠B的大小,并说明△ABC是等边三角形.解:在菱形ABCD中,
∵∠B+∠BAD=180°,
∠BAD=2∠B,
∴∠B=60°.
在菱形ABCD中,
∵AB=BC(菱形的四条边都相等),∠B=60°,
∴△ABC是等边三角形.知3-讲例3 如图,菱形ABCD的对角线AC与BD 相交于点O,AE垂直且平分CD,垂足为点E. 求∠BCD的大小.解:∵四边形ABCD是菱形,
∴AD=DC=CB=BA(菱形的
四条边都相等).
又∵AE垂直平分CD,
∴AC=AD,
∴AC=AD=DC=CB=BA,
即△ADC与△ABC都为等边三角形,
∴∠ACD=∠ACB=60°.
∴∠BCD=120°.知3-讲1 边长为3 cm的菱形的周长是( )
A.6 cm B.9 cm
C.12 cm D.15 cm
2 如图,在菱形ABCD中,AB=5,∠BCD=120°,则△ABC的周长等于( )
A.20
B.15
C.10
D.5知3-练4知识点菱形的对角线的性质知4-讲1.性质
(1)菱形的两条对角线互相垂直;
(2)菱形的每一条对角线平分一组对角;
(3)菱形具有平行四边形的一切性质;
2.菱形的面积计算:
①菱形的面积等于底乘高.
②菱形的面积等于对角线乘积的一半,对于对角线互相
垂直的四边形的面积都可以用两条对角线乘积的一半来
进行计算.3. 易错警示:
(1)菱形和矩形都是建立在平行四边形的基础上;
矩形是附加一直角;而菱形附加一组邻边相等;
(2)矩形的两条对角线把矩形分割成四个面积相等的
等腰三角形.而菱形的两条对角线把菱形分割成
四个全等的直角三角形;
(3)菱形的对称轴是两条对角线所在的直线,不要误
认为两条对角线是它的对称轴.知4-讲例4 如图,已知菱形ABCD的边长为 2 cm,∠BAD=120°,对角线AC、BD相交于点O. 试求这 个菱
形的两条对角线AC与BD的长. (结果保留根号)知4-讲解:∵四边形ABCD是菱形,
∴OB=OD,AB=AD(菱形的四条边都相等).
在△ABO和△ADO中,
∵AB=AD,AO=AO, OB=OD,
∴△ABO≌△ADO,
∴∠BAO=∠DAO = ∠BAD=60°.
在△ABC中,∵AB=BC,∠BAC=60°,
∴△ABC为等边三角形,∴AC=AB=2.知4-讲在菱形ABCD中,
∵AC⊥BD(菱形的对角线互相垂直),
∴△AOB为直角三角形,
∴
∴知4-讲例5 如图,在菱形ABCD中,对角线AC与BD相交于
点O,BD=6 cm,AC=4 cm. 求菱形的周长.知4-讲导引:由于菱形的四条边都相等,
所以要求其周长就要先求
出其边长.由菱形的性质
可知,其对角线互相垂直
平分,因此可以在直角三
角形中利用勾股定理来进
行计算.解:∵四边形ABCD是菱形,
∴AC⊥BD,AO= AC,BO= BD.
∵AC=4 cm,BD=6 cm,
∴AO=2 cm,BO=3 cm.
在Rt△ABO中,由勾股定理,得
∴菱形的周长=4AB= 知4-讲 菱形的对角线将菱形分成四个全等的直角三角
形,我们通常将菱形问题中求相关线段的长转化为
求直角三角形问题中相关线段的长,再利用勾股定
理来计算.知4-讲1 如图,在菱形ABCD中,AB=5,OA=4.求菱形
的周长与两条对角线的长度.
2 试说明菱形的面积等于它的
两条对角线长的乘积的一半.知4-练3 菱形具有而一般平行四边形不具有的
性质是( )
A.对边相等 B.对角相等
C.对角线互相平分 D.对角线互相垂直
4 如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH等于( )
A. B. C.5 D.4知4-练1.菱形具有平行四边形的一切性质.
2.菱形的每一条对角线平分一组对角.
3.菱形面积等于两对角线的长度乘积的一半.
4.菱形是中心对称图形,对称中心是两条对角线的交
点,菱形也是轴对称图形.
5.利用菱形的对角线计算线段的长度时,通常要借助
勾股定理来进行.
注意:菱形的对角线互相垂直平分,但不一定相等.1. 必做: 完成教材P112练习T3,
P113练习T1-3
2. 补充: 请完成练习册剩余部分习题
