19.2.2 菱形的判定 课件
图片预览








文档简介
课件26张PPT。19.2.2 菱形的判定1课堂讲解由边的数量关系判定菱形
由对角线的位置关系判定菱形2课时流程逐点
导讲练课堂小结作业提升 我们已经知道,有一组邻边相等的平行四边形是
菱形,这是菱形的定义.我们可以根据定义来判定一个
四边形是否是菱形.除此之外,还能找到其他的判定方
法吗?1知识点由边的数量关系判定菱形知1-导试一试
如图,作一个四条边都相等的四边形.
步骤:
1.画两条相等的线段AB、AD;
2.分别以点B和点D为圆心、AB长为半径画弧,两 弧相交
于点C;
3.连结BC、CD,即得一个四条边都相等的四边形 ABCD.
观察你所画的图形,它是菱形吗?知1-讲判定方法:
(1)(定义法):一组邻边相等的平行四边形是菱形;
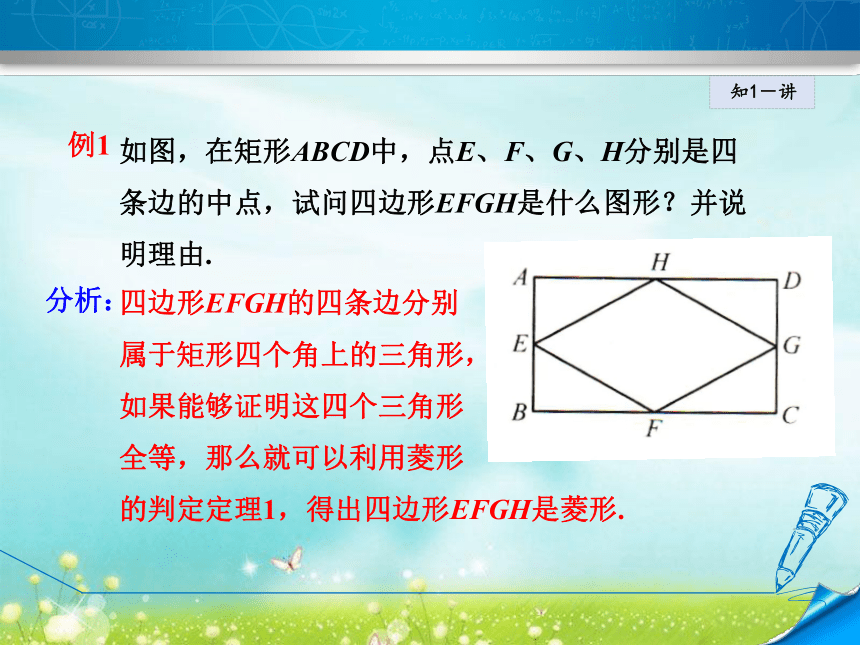
(2)(边):四条边相等的四边形是菱形;知1-讲例1 如图,在矩形ABCD中,点E、F、G、H分别是四条边的中点,试问四边形EFGH是什么图形?并说明理由. 分析:四边形EFGH的四条边分别
属于矩形四个角上的三角形,
如果能够证明这四个三角形
全等,那么就可以利用菱形
的判定定理1,得出四边形EFGH是菱形.知1-讲例2 如图,在四边形ABCD中,AD∥BC,AB=CD,
点E,F,G,H分别是AD,BD,BC,AC的中点.
试说明:四边形EFGH是菱形.分析:由于点E,F,G,H分别是AD,
BD,BC,AC的中点,可知EH,
HG,GF,FE分别是△ACD,
△ABC,△BCD,△ABD的中
位线,又∵AB=CD,
∴EH=HG=GF=FE,根据“四条边相等的四边形
是菱形”可得四边形EFGH是菱形.知1-讲∵点E,H分别为AD,AC的中点,
∴EH为△ACD的中位线,
∴EH= CD.
同理可证:
EF= AB,FG= CD,HG= AB.
又∵AB=CD,
∴EH=EF=FG=HG,
∴四边形EFGH是菱形.解: 有较多线段相等的条件时,我们可考虑通过证
明四条边相等来证明四边形是菱形.
注意:本例也可以通过先证四边形EFGH是平行四
边形,再证一组邻边相等,只不过步骤复杂一点,
读者不妨试一试.知1-讲知1-讲例3 如图,在 ABCD中,对角线AC、BD互相垂直,只需证明有一组邻边相等,即可得到 ABCD是菱形.证明:∵四边形ABCD是平行四边形,
∴OA=OC.
又∵AC⊥BD,
∴BD所在直线是线段AC的垂直平分线,
∴AB=BC,
∴四边形ABCD是菱形(有一组邻边相等的平行四边
形是菱形).1 如图,在四边形ABCD中,AD∥BC,AB=AD,∠BAD的平分线AE交BC于点E,连结DE.
求证:四边形ABED是菱形.知1-练2 如图,在△ABC中,点D是BC的中点,点E,F分别在线段AD及其延长线上,且DE=DF.给出下列条件:
①BE⊥EC;
②BF∥CE;
③AB=AC.
从中选择一个条件使四边形BECF是菱形,你认为这个条件是________.(只填写序号)知1-练3 如图,要使 ABCD为菱形,则需添加
的一个条件是( )
A.AC=AD
B.BA=BC
C.∠ABC=90°
D.AC=BD知1-练4 如图,将△ABC沿BC方向平移得到△DCE,连结AD,下列条件能够判定四边形ABCD为菱形的是
( )
A.AB=BC
B.AC=BC
C.∠B=60°
D.∠ACB=60°知1-练2知识点由对角线的位置关系判定菱形知2-导 用一长一短两根木条,在它们的中点处固定一个
小钉,做成一个可转动的十字,四周围上一根橡皮筋,
做成一个四边形.转动木条,这个四边形什么时候变
成菱形?知2-讲判定方法:(3)(对角线)对角线互相垂直的平行四边形是菱形.
要点精析:
(1)判定菱形时,一定要明确前提条件是从“四边形”出发
的,还是从“平行四边形”出发的:
①若从“四边形”出发,则还需四条边相等;
②若从“平行四边形”出发,则还需一组邻边相等或对
角线互相垂直.
(2)判定菱形的方法:①若用对角线进行判定:先证明四边
形是平行四边形,再证明对角线互相垂直,或直接证明
四边形的对角线互相垂直平分;②若用边进行判定:先
证明四边形是平行四边形,再证明一组邻边相等,或直
接证明四边形的四条边都相等.知2-讲例4 如图,已知矩形ABCD的对角线AC的垂直平分线与边AD、BC分别交于点E、F.
求证:四边形AFCE是菱形.分析:要证四边形AFCE是菱形,
由已知条件可知 EF⊥AC,
所以只需证明四边形AFCE
是平行四边形,又 知EF垂
直平分AC,所以只需证明
OE=OF.知2-讲∵四边形ABCD是矩形,∴AE∥FC,
∴∠1=∠2.
∵EF平分AC,∴OA=OC.
又∵∠AOE=∠COF=90°,
∴△AOE≌△COF, ∴OE=OF,
∴四边形AFCE是平行四边形.
又∵EF⊥AC,
∴四边形AFCE是菱形(对角线互相垂直的平行四
边形是菱形).证明:知2-讲例5 如图,在平行四边形ABCD中,对角线AC,BD相交于点O,过点O作直线EF⊥BD,分别交AD,BC于点E和点F,连结BE,DF.求证:四边形BEDF是菱形.导引:若要证明四边形BEDF是
菱形,由EF⊥BD只需要
证明四边形BEDF是平行
四边形,而DE∥BF,只
需要证明DE=BF,即可判定四边形BEDF是平行
四边形,证明DE=BF可通过证明△OED≌△OFB
来证明.知2-讲∵四边形ABCD是平行四边形,
∴OB=OD,AD∥BC,
∴∠EDO=∠FBO,∠OED=∠OFB,
∴△OED≌△OFB,
∴DE=BF,
又∵DE∥BF,
∴四边形BEDF是平行四边形.
∵EF⊥BD,
∴四边形BEDF是菱形.证明:证明一个四边形是菱形的方法:
若已知要证的四边形的对角线互相垂直,则要
考虑证明这个四边形是平行四边形.知2-讲1 作一个菱形,使它的两条对角线的长分别为6 cm和
8 cm,并说明其理由.
2 如图, ABCD的对角线AC,BD相交于点O,请你添加一个适当的条件__________使其成为菱形.(只填一个即可)知2-练知2-练3 如图,在 ABCD中,对角线AC与BD
交于点O,若增加一个条件,使 ABCD成为菱形,
下列给出的条件不正确的是( )
A.AB=AD
B.AC⊥BD
C.AC=BD
D.∠BAC=∠DAC知2-练4 下列条件:
①四边相等的四边形;
②对角线互相垂直且平分的四边形;
③一组邻边相等的四边形;
④一条对角线平分一组对角的平行四边形.
其中能判定四边形是菱形的有( )
A.1个 B.2个 C.3个 D.4个1.判定菱形的常见思路:
2.判定一个四边形是菱形的方法:若已知一组邻边相等要
证明一个四边形是菱形,有两条路可走:①证明四条边
都相等,利用四条边相等的四边形是菱形来证;②证明
是平行四边形,利用有一组邻边相等的平行四边形是菱
形.若条件中出现两条对角线,要证明一个四边形是菱
形,可考虑利用:①对角线互相垂直平分的四边形是菱
形;②对角线互相垂直的平行四边形是菱形.1.必做: 完成教材P115练习T3,
P118练习T2-3
2.补充: 请完成练习册剩余部分习题
由对角线的位置关系判定菱形2课时流程逐点
导讲练课堂小结作业提升 我们已经知道,有一组邻边相等的平行四边形是
菱形,这是菱形的定义.我们可以根据定义来判定一个
四边形是否是菱形.除此之外,还能找到其他的判定方
法吗?1知识点由边的数量关系判定菱形知1-导试一试
如图,作一个四条边都相等的四边形.
步骤:
1.画两条相等的线段AB、AD;
2.分别以点B和点D为圆心、AB长为半径画弧,两 弧相交
于点C;
3.连结BC、CD,即得一个四条边都相等的四边形 ABCD.
观察你所画的图形,它是菱形吗?知1-讲判定方法:
(1)(定义法):一组邻边相等的平行四边形是菱形;
(2)(边):四条边相等的四边形是菱形;知1-讲例1 如图,在矩形ABCD中,点E、F、G、H分别是四条边的中点,试问四边形EFGH是什么图形?并说明理由. 分析:四边形EFGH的四条边分别
属于矩形四个角上的三角形,
如果能够证明这四个三角形
全等,那么就可以利用菱形
的判定定理1,得出四边形EFGH是菱形.知1-讲例2 如图,在四边形ABCD中,AD∥BC,AB=CD,
点E,F,G,H分别是AD,BD,BC,AC的中点.
试说明:四边形EFGH是菱形.分析:由于点E,F,G,H分别是AD,
BD,BC,AC的中点,可知EH,
HG,GF,FE分别是△ACD,
△ABC,△BCD,△ABD的中
位线,又∵AB=CD,
∴EH=HG=GF=FE,根据“四条边相等的四边形
是菱形”可得四边形EFGH是菱形.知1-讲∵点E,H分别为AD,AC的中点,
∴EH为△ACD的中位线,
∴EH= CD.
同理可证:
EF= AB,FG= CD,HG= AB.
又∵AB=CD,
∴EH=EF=FG=HG,
∴四边形EFGH是菱形.解: 有较多线段相等的条件时,我们可考虑通过证
明四条边相等来证明四边形是菱形.
注意:本例也可以通过先证四边形EFGH是平行四
边形,再证一组邻边相等,只不过步骤复杂一点,
读者不妨试一试.知1-讲知1-讲例3 如图,在 ABCD中,对角线AC、BD互相垂直,只需证明有一组邻边相等,即可得到 ABCD是菱形.证明:∵四边形ABCD是平行四边形,
∴OA=OC.
又∵AC⊥BD,
∴BD所在直线是线段AC的垂直平分线,
∴AB=BC,
∴四边形ABCD是菱形(有一组邻边相等的平行四边
形是菱形).1 如图,在四边形ABCD中,AD∥BC,AB=AD,∠BAD的平分线AE交BC于点E,连结DE.
求证:四边形ABED是菱形.知1-练2 如图,在△ABC中,点D是BC的中点,点E,F分别在线段AD及其延长线上,且DE=DF.给出下列条件:
①BE⊥EC;
②BF∥CE;
③AB=AC.
从中选择一个条件使四边形BECF是菱形,你认为这个条件是________.(只填写序号)知1-练3 如图,要使 ABCD为菱形,则需添加
的一个条件是( )
A.AC=AD
B.BA=BC
C.∠ABC=90°
D.AC=BD知1-练4 如图,将△ABC沿BC方向平移得到△DCE,连结AD,下列条件能够判定四边形ABCD为菱形的是
( )
A.AB=BC
B.AC=BC
C.∠B=60°
D.∠ACB=60°知1-练2知识点由对角线的位置关系判定菱形知2-导 用一长一短两根木条,在它们的中点处固定一个
小钉,做成一个可转动的十字,四周围上一根橡皮筋,
做成一个四边形.转动木条,这个四边形什么时候变
成菱形?知2-讲判定方法:(3)(对角线)对角线互相垂直的平行四边形是菱形.
要点精析:
(1)判定菱形时,一定要明确前提条件是从“四边形”出发
的,还是从“平行四边形”出发的:
①若从“四边形”出发,则还需四条边相等;
②若从“平行四边形”出发,则还需一组邻边相等或对
角线互相垂直.
(2)判定菱形的方法:①若用对角线进行判定:先证明四边
形是平行四边形,再证明对角线互相垂直,或直接证明
四边形的对角线互相垂直平分;②若用边进行判定:先
证明四边形是平行四边形,再证明一组邻边相等,或直
接证明四边形的四条边都相等.知2-讲例4 如图,已知矩形ABCD的对角线AC的垂直平分线与边AD、BC分别交于点E、F.
求证:四边形AFCE是菱形.分析:要证四边形AFCE是菱形,
由已知条件可知 EF⊥AC,
所以只需证明四边形AFCE
是平行四边形,又 知EF垂
直平分AC,所以只需证明
OE=OF.知2-讲∵四边形ABCD是矩形,∴AE∥FC,
∴∠1=∠2.
∵EF平分AC,∴OA=OC.
又∵∠AOE=∠COF=90°,
∴△AOE≌△COF, ∴OE=OF,
∴四边形AFCE是平行四边形.
又∵EF⊥AC,
∴四边形AFCE是菱形(对角线互相垂直的平行四
边形是菱形).证明:知2-讲例5 如图,在平行四边形ABCD中,对角线AC,BD相交于点O,过点O作直线EF⊥BD,分别交AD,BC于点E和点F,连结BE,DF.求证:四边形BEDF是菱形.导引:若要证明四边形BEDF是
菱形,由EF⊥BD只需要
证明四边形BEDF是平行
四边形,而DE∥BF,只
需要证明DE=BF,即可判定四边形BEDF是平行
四边形,证明DE=BF可通过证明△OED≌△OFB
来证明.知2-讲∵四边形ABCD是平行四边形,
∴OB=OD,AD∥BC,
∴∠EDO=∠FBO,∠OED=∠OFB,
∴△OED≌△OFB,
∴DE=BF,
又∵DE∥BF,
∴四边形BEDF是平行四边形.
∵EF⊥BD,
∴四边形BEDF是菱形.证明:证明一个四边形是菱形的方法:
若已知要证的四边形的对角线互相垂直,则要
考虑证明这个四边形是平行四边形.知2-讲1 作一个菱形,使它的两条对角线的长分别为6 cm和
8 cm,并说明其理由.
2 如图, ABCD的对角线AC,BD相交于点O,请你添加一个适当的条件__________使其成为菱形.(只填一个即可)知2-练知2-练3 如图,在 ABCD中,对角线AC与BD
交于点O,若增加一个条件,使 ABCD成为菱形,
下列给出的条件不正确的是( )
A.AB=AD
B.AC⊥BD
C.AC=BD
D.∠BAC=∠DAC知2-练4 下列条件:
①四边相等的四边形;
②对角线互相垂直且平分的四边形;
③一组邻边相等的四边形;
④一条对角线平分一组对角的平行四边形.
其中能判定四边形是菱形的有( )
A.1个 B.2个 C.3个 D.4个1.判定菱形的常见思路:
2.判定一个四边形是菱形的方法:若已知一组邻边相等要
证明一个四边形是菱形,有两条路可走:①证明四条边
都相等,利用四条边相等的四边形是菱形来证;②证明
是平行四边形,利用有一组邻边相等的平行四边形是菱
形.若条件中出现两条对角线,要证明一个四边形是菱
形,可考虑利用:①对角线互相垂直平分的四边形是菱
形;②对角线互相垂直的平行四边形是菱形.1.必做: 完成教材P115练习T3,
P118练习T2-3
2.补充: 请完成练习册剩余部分习题
