19.3.2 正方形的判定 课件
图片预览









文档简介
课件32张PPT。19.3.2 正方形的判定1课堂讲解正方形面积的性质
正方形的判定2课时流程逐点
导讲练课堂小结作业提升(1)正方形是怎样的平行四边形?
(2)正方形是怎样的矩形?
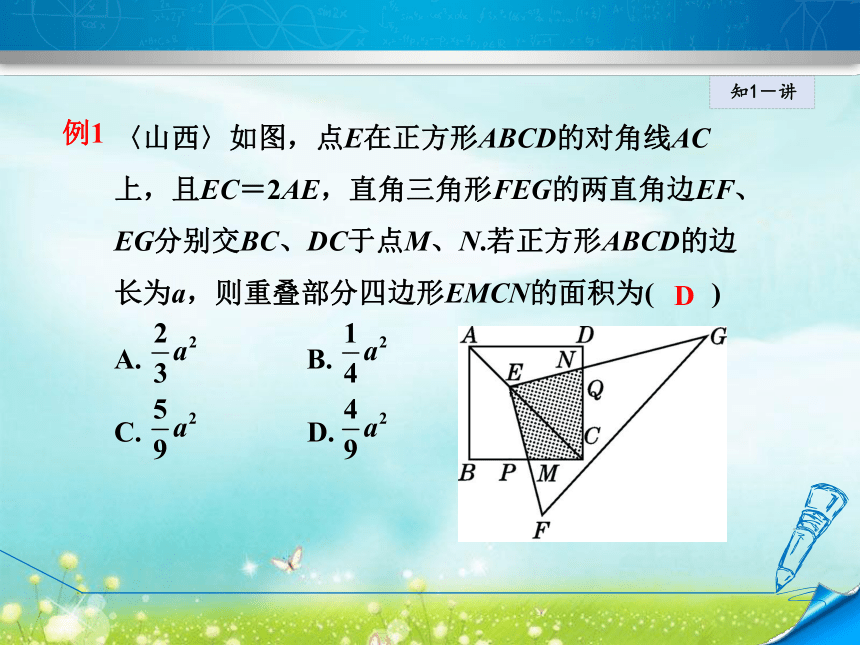
(3)正方形是怎样的菱形?1知识点正方形面积的性质知1-讲正方形面积等于边长的平方或对角线平方的一半.知1-讲例1 〈山西〉如图,点E在正方形ABCD的对角线AC
上,且EC=2AE,直角三角形FEG的两直角边EF、EG分别交BC、DC于点M、N.若正方形ABCD的边长为a,则重叠部分四边形EMCN的面积为( )
A. B.
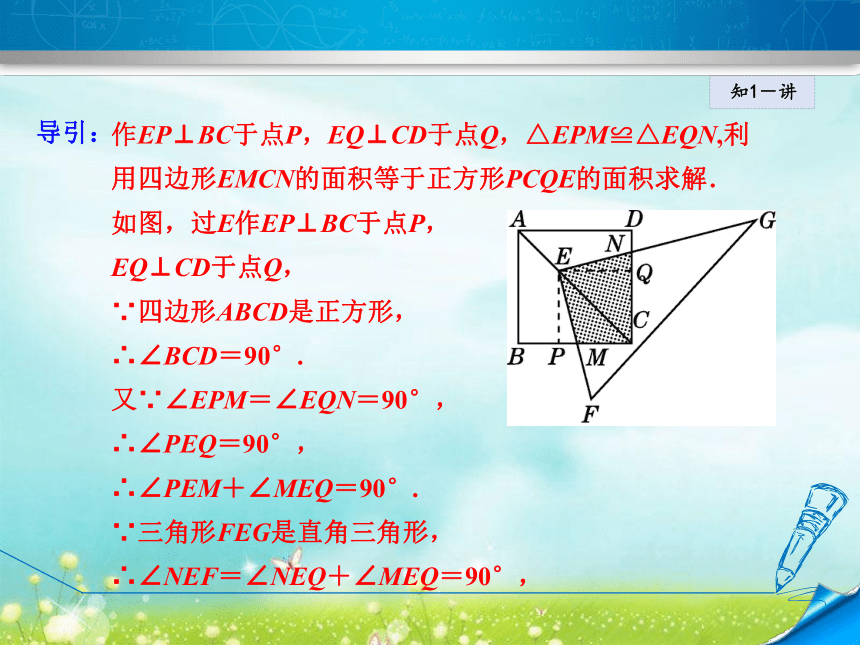
C. D. D知1-讲导引:作EP⊥BC于点P,EQ⊥CD于点Q,△EPM≌△EQN,利
用四边形EMCN的面积等于正方形PCQE的面积求解.
如图,过E作EP⊥BC于点P,
EQ⊥CD于点Q,
∵四边形ABCD是正方形,
∴∠BCD=90°.
又∵∠EPM=∠EQN=90°,
∴∠PEQ=90°,
∴∠PEM+∠MEQ=90°.
∵三角形FEG是直角三角形,
∴∠NEF=∠NEQ+∠MEQ=90°,知1-讲∴∠PEM=∠NEQ.
∵CA是∠BCD的平分线,∠EPC=∠EQC=90°,
∴EP=EQ,四边形PCQE是正方形.
在△EPM和△EQN中,
∴△EPM≌△EQN(ASA).
∴S△EQN=S△EPM,
∴四边形EMCN的面积等于正方形PCQE的面积.
∵正方形ABCD的边长为a,∴AC=
∵EC=2AE,∴EC= 知1-讲∴EP=PC=
∴正方形PCQE的面积=
∴四边形EMCN的面积= 本例解法在于巧用割补法,将分散的图形拼合
在一起,将不规则的阴影面积集中到一个规则的正
方形中,再利用正方形的性质求出,解答过程体现
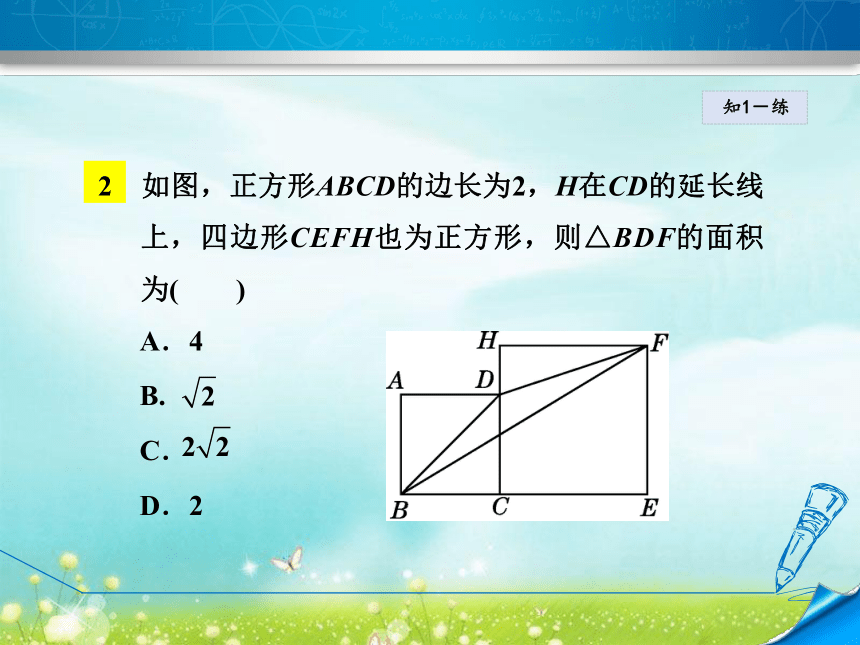
了割补法及转化思想.知1-讲1 如图,菱形ABCD的面积为120 cm2,正方形AECF的面积为50 cm2,则菱形的边长为________.知1-练2 如图,正方形ABCD的边长为2,H在CD的延长线上,四边形CEFH也为正方形,则△BDF的面积为( )
A.4
B.
C.
D.2知1-练2知识点正方形的判定知2-导讨论
老师给学生一个任务:从一张彩色纸中剪出一个正方
形.
小明剪完后,这样检验它:比较边的长度,发现四条
边是相等的,于是就判定自己完成了这个任务.这种检验 可
信吗?
小兵用另一种方法检验:他量的不是边,而是对角线,
发现对角线是相等的,于是就认为自己正确地剪出了正方
形. 这种检验对吗?知2-导 小英剪完后,比较了由对角线相互分成的4条线
段, 发现它们是相等的.按照小英的意见,这说明剪
出的四边形是正方形. 你的意见怎样?
你认为应该如何检验,才能又快又准确呢?知2-讲1.判定方法:
(1)从四边形出发:①有四条边相等,四个角都是直角的
四边形是正方形;②对角线互相平分、垂直且相等的
四边形是正方形;
(2)从平行四边形出发:①有一组邻边相等并且有一个角
是直角的平行四边形是正方形;②对角线互相垂直且
相等的平行四边形是正方形;
(3)从矩形出发:①有一组邻边相等的矩形是正方形;
②对角线互相垂直的矩形是正方形;
(4)从菱形出发:①有一个角是直角的菱形是正方形;
②对角线相等的菱形是正方形.知2-讲2.四边形间的关系:
(1)四边形、平行四边形、矩形、菱形、正方形间的
包含关系如图.知2-讲(2)四边形、平行四边形、矩形、菱形、正方形间的
转化关系如图:知2-讲例2 如图,在△ABC中,∠C=90°,CD平分∠ACB,DE⊥BC,DF⊥AC,垂足分别为E,F.
求证:四边形CFDE是正方形.要证四边形CFDE是正方
形,首先要确定这个正方
形建立在哪种四边形的基
础上,即先证它是什么四
边形;再证这种四边形是
正方形需要补充的条件.导引:知2-讲∵DE⊥BC,AC⊥BC,∴DE∥CF.
同理DF∥CE,
∴四边形CFDE是平行四边形.
∵CD平分∠ACB,DE⊥BC,DF⊥AC,
∴DE=DF,∴ CFDE是菱形.
∵∠ACB=90°,∴菱形CFDE是正方形.
∵∠ECF=∠CFD=∠CED=90°,
∴四边形CFDE是矩形.
∵CD平分∠ACB,DE⊥BC,DF⊥AC,
∴DE=DF,∴矩形CFDE是正方形.证法一:证法二:证明条件中不含对角线的四边形是正方形的四种方法:
方法1:证:“四边形+四边相等+四个直角”;
方法2:证:“平行四边形+一组邻边相等+一个直角”;
方法3:证:“矩形+一组邻边相等”;
方法4:证:“菱形+一个直角”.
说明:在判定四边形是正方形时,四边形常常是建
立在矩形或菱形的基础上,采用方法3、方法4进行证明;
如证明中的证法一、证法二;本例也可采用方法1、方法
2,请读者去试一试.知2-讲知2-讲例3 如图,已知在 ABCD中,对角线AC,BD交于点
O,E是BD的延长线上的点,且EA=EC.
(1)求证:四边形ABCD是菱形;
(2)若∠DAC=∠EAD+∠AED,求证:四边形
ABCD是正方形.知2-讲要证 ABCD是正方形有三种途径可走:即在平行四边
形、菱形、矩形的基础上,找各需补充的对角线的条件
进行证明;若要证明 ABCD是菱形,由于题中条件与
对角线相关,则需证AC⊥BD.
(1)首先根据平行四边形的性质可得AO=CO,再由
EA=EC可得△EAC是等腰三角形,然后根据等腰三角
形三线合一的性质可得EO⊥AC,根据对角线互相垂直
的平行四边形是菱形可证出结论;
(2)首先根据角的关系得出AO=DO,进而得到AC
=BD,再根据对角线相等的菱形是正方形可得到结论.导引:知2-讲(1)∵四边形ABCD是平行四边形,
∴AO=CO.
又∵EA=EC,∴EO⊥AC,即BD⊥AC,
∴四边形ABCD是菱形.
(2)∵∠ADO=∠EAD+∠AED,
∠DAC=∠EAD+∠AED,
∴∠ADO=∠DAC,∴AO=DO.
∵四边形ABCD是菱形,
∴AC=2AO,BD=2DO,∴AC=BD,
∴四边形ABCD是正方形.证明:证明条件中含对角线的四边形是正方形的方法:
(1)证:“四边形+对角线互相垂直、平分且相等”;
(2)证:“平行四边形+对角线互相垂直且相等”;
(3)证:“矩形+对角线互相垂直”;
(4)证:“菱形+对角线相等”.
证明一个四边形是正方形的方法:结合条件选择合理的
判定方法,一般先证明是矩形,然后找出一组邻边相等
或对角线互相垂直;或者先证明是菱形,然后找一个角
是直角或对角线相等.知2-讲知2-讲例4 已知:如图,在四边形ABCD中,AC⊥BD,AC=
BD,E、F、G、H分别为AB、BC、CD、DA的中点.
求证:四边形EFGH是正方形.要证四边形EFGH是正方形,
以四边形、平行四边形、矩
形、菱形为基础都可以证出
所要证的结论;若以四边形
为基础,则只需证明四条边
相等,四个角是直角即可.导引:知2-讲∵E、F、G、H分别为四边形ABCD各边的中点,
∴EF∥GH∥AC,FG∥EH∥BD,
且EF=GH= AC,FG=EH= BD.
又∵AC⊥BD,AC=BD,
∴∠HEF=∠EFG=∠GHE=∠FGH=90°,
EF=FG=GH=HE.
∴四边形EFGH是正方形.证明:几种常见的中点四边形的命题:
(1)连结四边形各边中点的四边形是平行四边形;
(2)连结对角线互相垂直的四边形各边中点的四边形是矩形;
(3)连结对角线相等的四边形各边中点的四边形是菱形;
(4)连结平行四边形各边中点的四边形是平行四边形;
(5)连结矩形各边中点的四边形是菱形;
(6)连结菱形各边中点的四边形是矩形.知2-讲知2-讲 中点四边形的形状是由外围四边形的对角线之间的
关系确定的.任意四边形的中点四边形是平行四边形;
对角线相等的四边形的中点四边形是菱形;对角线互相
垂直的四边形的中点四边形是矩形;对角线相等且互相
垂直的四边形的中点四边形是正方形.1 把一张矩形纸片如图那样折一下就可以裁出正方
形纸片,为什么?知2-练知2-练2 ABCD的对角线AC与BD相交于点O,且AC⊥BD,请添加一个条件:________,使得
ABCD为正方形.
3 下列判断错误的是( )
A.两组对边分别相等的四边形是平行四边形
B.四个内角都相等的四边形是矩形
C.四条边都相等的四边形是菱形
D.两条对角线垂直且互相平分的四边形是正方形知2-练4 小明在学习了正方形之后,给同桌小文出了道题,从下列四个条件:
①AB=BC;②∠ABC=90°;
③AC=BD;④AC⊥BD中选两个作为补充条件,使 ABCD为正方形(如图),现有下列四种选法,你认为其中错误的是( )
A.①② B.②③
C.①③ D.②④有一个角是直角有一组邻边相等有一组邻边相等并且有一个角是直角有一组邻边相等有一个角是直角1.必做: 完成教材P121练习T2-3
2.补充: 请完成练习册剩余部分习题
正方形的判定2课时流程逐点
导讲练课堂小结作业提升(1)正方形是怎样的平行四边形?
(2)正方形是怎样的矩形?
(3)正方形是怎样的菱形?1知识点正方形面积的性质知1-讲正方形面积等于边长的平方或对角线平方的一半.知1-讲例1 〈山西〉如图,点E在正方形ABCD的对角线AC
上,且EC=2AE,直角三角形FEG的两直角边EF、EG分别交BC、DC于点M、N.若正方形ABCD的边长为a,则重叠部分四边形EMCN的面积为( )
A. B.
C. D. D知1-讲导引:作EP⊥BC于点P,EQ⊥CD于点Q,△EPM≌△EQN,利
用四边形EMCN的面积等于正方形PCQE的面积求解.
如图,过E作EP⊥BC于点P,
EQ⊥CD于点Q,
∵四边形ABCD是正方形,
∴∠BCD=90°.
又∵∠EPM=∠EQN=90°,
∴∠PEQ=90°,
∴∠PEM+∠MEQ=90°.
∵三角形FEG是直角三角形,
∴∠NEF=∠NEQ+∠MEQ=90°,知1-讲∴∠PEM=∠NEQ.
∵CA是∠BCD的平分线,∠EPC=∠EQC=90°,
∴EP=EQ,四边形PCQE是正方形.
在△EPM和△EQN中,
∴△EPM≌△EQN(ASA).
∴S△EQN=S△EPM,
∴四边形EMCN的面积等于正方形PCQE的面积.
∵正方形ABCD的边长为a,∴AC=
∵EC=2AE,∴EC= 知1-讲∴EP=PC=
∴正方形PCQE的面积=
∴四边形EMCN的面积= 本例解法在于巧用割补法,将分散的图形拼合
在一起,将不规则的阴影面积集中到一个规则的正
方形中,再利用正方形的性质求出,解答过程体现
了割补法及转化思想.知1-讲1 如图,菱形ABCD的面积为120 cm2,正方形AECF的面积为50 cm2,则菱形的边长为________.知1-练2 如图,正方形ABCD的边长为2,H在CD的延长线上,四边形CEFH也为正方形,则△BDF的面积为( )
A.4
B.
C.
D.2知1-练2知识点正方形的判定知2-导讨论
老师给学生一个任务:从一张彩色纸中剪出一个正方
形.
小明剪完后,这样检验它:比较边的长度,发现四条
边是相等的,于是就判定自己完成了这个任务.这种检验 可
信吗?
小兵用另一种方法检验:他量的不是边,而是对角线,
发现对角线是相等的,于是就认为自己正确地剪出了正方
形. 这种检验对吗?知2-导 小英剪完后,比较了由对角线相互分成的4条线
段, 发现它们是相等的.按照小英的意见,这说明剪
出的四边形是正方形. 你的意见怎样?
你认为应该如何检验,才能又快又准确呢?知2-讲1.判定方法:
(1)从四边形出发:①有四条边相等,四个角都是直角的
四边形是正方形;②对角线互相平分、垂直且相等的
四边形是正方形;
(2)从平行四边形出发:①有一组邻边相等并且有一个角
是直角的平行四边形是正方形;②对角线互相垂直且
相等的平行四边形是正方形;
(3)从矩形出发:①有一组邻边相等的矩形是正方形;
②对角线互相垂直的矩形是正方形;
(4)从菱形出发:①有一个角是直角的菱形是正方形;
②对角线相等的菱形是正方形.知2-讲2.四边形间的关系:
(1)四边形、平行四边形、矩形、菱形、正方形间的
包含关系如图.知2-讲(2)四边形、平行四边形、矩形、菱形、正方形间的
转化关系如图:知2-讲例2 如图,在△ABC中,∠C=90°,CD平分∠ACB,DE⊥BC,DF⊥AC,垂足分别为E,F.
求证:四边形CFDE是正方形.要证四边形CFDE是正方
形,首先要确定这个正方
形建立在哪种四边形的基
础上,即先证它是什么四
边形;再证这种四边形是
正方形需要补充的条件.导引:知2-讲∵DE⊥BC,AC⊥BC,∴DE∥CF.
同理DF∥CE,
∴四边形CFDE是平行四边形.
∵CD平分∠ACB,DE⊥BC,DF⊥AC,
∴DE=DF,∴ CFDE是菱形.
∵∠ACB=90°,∴菱形CFDE是正方形.
∵∠ECF=∠CFD=∠CED=90°,
∴四边形CFDE是矩形.
∵CD平分∠ACB,DE⊥BC,DF⊥AC,
∴DE=DF,∴矩形CFDE是正方形.证法一:证法二:证明条件中不含对角线的四边形是正方形的四种方法:
方法1:证:“四边形+四边相等+四个直角”;
方法2:证:“平行四边形+一组邻边相等+一个直角”;
方法3:证:“矩形+一组邻边相等”;
方法4:证:“菱形+一个直角”.
说明:在判定四边形是正方形时,四边形常常是建
立在矩形或菱形的基础上,采用方法3、方法4进行证明;
如证明中的证法一、证法二;本例也可采用方法1、方法
2,请读者去试一试.知2-讲知2-讲例3 如图,已知在 ABCD中,对角线AC,BD交于点
O,E是BD的延长线上的点,且EA=EC.
(1)求证:四边形ABCD是菱形;
(2)若∠DAC=∠EAD+∠AED,求证:四边形
ABCD是正方形.知2-讲要证 ABCD是正方形有三种途径可走:即在平行四边
形、菱形、矩形的基础上,找各需补充的对角线的条件
进行证明;若要证明 ABCD是菱形,由于题中条件与
对角线相关,则需证AC⊥BD.
(1)首先根据平行四边形的性质可得AO=CO,再由
EA=EC可得△EAC是等腰三角形,然后根据等腰三角
形三线合一的性质可得EO⊥AC,根据对角线互相垂直
的平行四边形是菱形可证出结论;
(2)首先根据角的关系得出AO=DO,进而得到AC
=BD,再根据对角线相等的菱形是正方形可得到结论.导引:知2-讲(1)∵四边形ABCD是平行四边形,
∴AO=CO.
又∵EA=EC,∴EO⊥AC,即BD⊥AC,
∴四边形ABCD是菱形.
(2)∵∠ADO=∠EAD+∠AED,
∠DAC=∠EAD+∠AED,
∴∠ADO=∠DAC,∴AO=DO.
∵四边形ABCD是菱形,
∴AC=2AO,BD=2DO,∴AC=BD,
∴四边形ABCD是正方形.证明:证明条件中含对角线的四边形是正方形的方法:
(1)证:“四边形+对角线互相垂直、平分且相等”;
(2)证:“平行四边形+对角线互相垂直且相等”;
(3)证:“矩形+对角线互相垂直”;
(4)证:“菱形+对角线相等”.
证明一个四边形是正方形的方法:结合条件选择合理的
判定方法,一般先证明是矩形,然后找出一组邻边相等
或对角线互相垂直;或者先证明是菱形,然后找一个角
是直角或对角线相等.知2-讲知2-讲例4 已知:如图,在四边形ABCD中,AC⊥BD,AC=
BD,E、F、G、H分别为AB、BC、CD、DA的中点.
求证:四边形EFGH是正方形.要证四边形EFGH是正方形,
以四边形、平行四边形、矩
形、菱形为基础都可以证出
所要证的结论;若以四边形
为基础,则只需证明四条边
相等,四个角是直角即可.导引:知2-讲∵E、F、G、H分别为四边形ABCD各边的中点,
∴EF∥GH∥AC,FG∥EH∥BD,
且EF=GH= AC,FG=EH= BD.
又∵AC⊥BD,AC=BD,
∴∠HEF=∠EFG=∠GHE=∠FGH=90°,
EF=FG=GH=HE.
∴四边形EFGH是正方形.证明:几种常见的中点四边形的命题:
(1)连结四边形各边中点的四边形是平行四边形;
(2)连结对角线互相垂直的四边形各边中点的四边形是矩形;
(3)连结对角线相等的四边形各边中点的四边形是菱形;
(4)连结平行四边形各边中点的四边形是平行四边形;
(5)连结矩形各边中点的四边形是菱形;
(6)连结菱形各边中点的四边形是矩形.知2-讲知2-讲 中点四边形的形状是由外围四边形的对角线之间的
关系确定的.任意四边形的中点四边形是平行四边形;
对角线相等的四边形的中点四边形是菱形;对角线互相
垂直的四边形的中点四边形是矩形;对角线相等且互相
垂直的四边形的中点四边形是正方形.1 把一张矩形纸片如图那样折一下就可以裁出正方
形纸片,为什么?知2-练知2-练2 ABCD的对角线AC与BD相交于点O,且AC⊥BD,请添加一个条件:________,使得
ABCD为正方形.
3 下列判断错误的是( )
A.两组对边分别相等的四边形是平行四边形
B.四个内角都相等的四边形是矩形
C.四条边都相等的四边形是菱形
D.两条对角线垂直且互相平分的四边形是正方形知2-练4 小明在学习了正方形之后,给同桌小文出了道题,从下列四个条件:
①AB=BC;②∠ABC=90°;
③AC=BD;④AC⊥BD中选两个作为补充条件,使 ABCD为正方形(如图),现有下列四种选法,你认为其中错误的是( )
A.①② B.②③
C.①③ D.②④有一个角是直角有一组邻边相等有一组邻边相等并且有一个角是直角有一组邻边相等有一个角是直角1.必做: 完成教材P121练习T2-3
2.补充: 请完成练习册剩余部分习题
