19.1.1 矩形及其性质 课件+素材(2份打包)
文档属性
| 名称 | 19.1.1 矩形及其性质 课件+素材(2份打包) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-01-04 00:00:00 | ||
图片预览








文档简介
课件26张PPT。19.1.1 矩形及其性质1课堂讲解矩形的定义
矩形的边角性质
矩形的对角线性质2课时流程逐点
导讲练课堂小结作业提升什么是平行四边形?
平行四边形都有哪些性质?1知识点矩形的定义知1-导 如图,用四根木条做一个平行四边形的活动木框,
将其直立在地面上并轻轻推动,你会发现 什么?知1-讲定义:有一个角是直角的平行四边形叫做矩形.
注意:
(1)由矩形的定义知,矩形一定是平行四边形,但平
行四边形不一定是矩形.
(2)矩形必须具备两个条件:
①它是一个平行四边形;
②它有一个角是直角,这两个条件缺一不可. 知1-讲例1 下列说法正确的是( )
A.平行四边形是矩形
B.矩形不一定是平行四边形
C.有一个角是直角的四边形是矩形
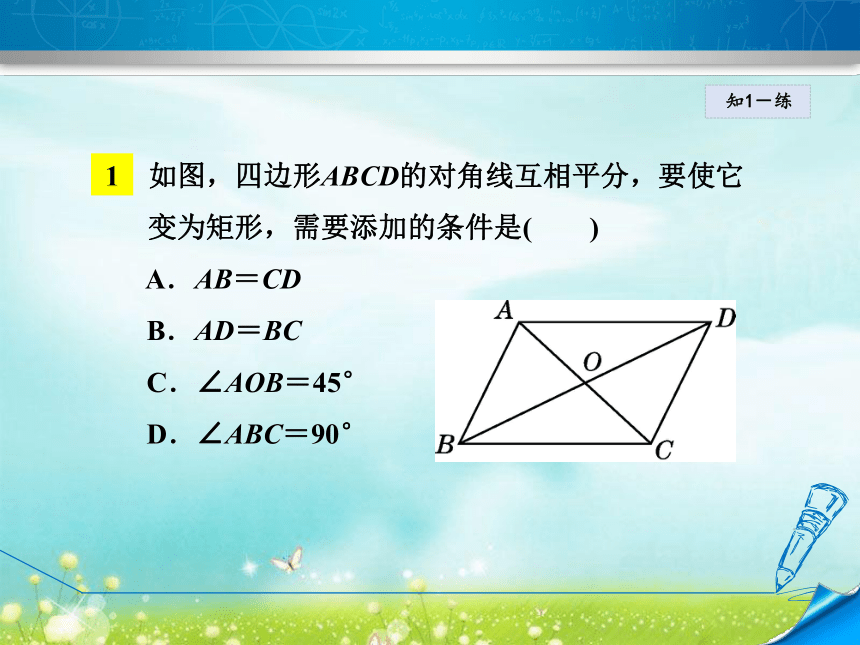
D.平行四边形具有的性质矩形都具有D1 如图,四边形ABCD的对角线互相平分,要使它
变为矩形,需要添加的条件是( )
A.AB=CD
B.AD=BC
C.∠AOB=45°
D.∠ABC=90°知1-练2 如图,小贤为了体验四边形的不稳定性,将四根木条用钉子钉成一个矩形框架ABCD,B与D两点之间用一根橡皮筋拉直固定,然后向右扭动框架,观察所得四边形的变化,下列判断错误的是( )
A.四边形ABCD由矩形变为平行四边形
B.BD的长度增大
C.四边形ABCD的面积不变
D.四边形ABCD的周长不变知1-练2知识点矩形的边角性质知2-讲性质:
(1)矩形的四个角都是直角.
(2)矩形具有平行四边形的所有性质.
(3)矩形是轴对称图形,如图所示, 邻边不相等的矩
形有两条对称轴.知2-讲要点精析:
(1)从边看:对边平行且相等;
(2)从角看:四个角都是直角;
(3)对称性:是中心对称图形,也是轴对称图形,邻边
不相等的矩形有两条对称轴;
(4)面积:
矩形的面积=长×宽;
矩形的面积=被对角线分成的四个等面积的小三角
形面积之和,
注:这四个小三角形是两对全等的等腰三角形.知2-讲例2 如图,在矩形ABCD中,AB =3,BC =4,BE⊥AC,垂足为点 E. 试求BE 的长.在矩形ABCD中, ∠ABC = 90°,解:又∵S△ABC1 如图,在矩形ABCD中,E是AD边上的一点.试说明△BCE的面积与矩形ABCD的面积之间的关系.知2-练知2-练2 如图,在矩形ABCD中,AB=6 cm,点E,F分别是边BC,AD上一点,将矩形ABCD沿EF折叠,使点C,D分别落在点C′,D′处.若C′E⊥AD,则EF的长为________cm.知2-练3 如图,点E是矩形ABCD的边AD延长线上的一点,且AD=DE,连结BE交CD于点O,连结AO,下列结论中不正确的是( )
A.△AOB≌△BOC
B.△BOC≌△EOD
C.△AOD≌△EOD
D.△AOD≌△BOC3知识点矩形的对角线性质知3-讲矩形的性质定理 2 矩形的对角线相等.知3-讲例3 如图,矩形ABCD被两条对角线分成四个小三角形, 如果四个小三角形周长的和是86 cm, 矩形的对角线长是13 cm,那么该矩形的周长是多少?∵△AOB、△BOC、△COD和△AOD四个小三角
形周长的和为86 cm.
∴AB+BC+CD+DA+2(OA+OB+OC+OD)
=AB+BC+CD+DA+2(AC+BD)
=86.
又∵AC=BD=13(矩形的对角线相等),
∴AB+BC+CD+DA=86-2(AC+BD)
=86-4×13=34(cm),
即矩形ABCD的周长等于34 cm.解:知3-讲知3-讲例4 如图,在矩形ABCD中,对角线AC与BD相交于点O,AE垂直且平分线段BO,垂足为点E,BD=15 cm.
求AC、AB的长.∵四边形ABCD是矩形,
∴AC=BD=15(矩形的
对角线相等),
∴AO= AC=7. 5.
∵AE垂直平分BO,
∴AB=AO=7. 5.
即AC的长为15 cm,AB的长为7. 5 cm.解:知3-讲例5 如图,在矩形ABCD(AB>AD)中,△AOB与△AOD的周长的差为2 cm,和为34 cm,两条对角线长的和为20 cm,求矩形的周长和面积.知3-讲要求矩形的周长和面积,只需求出矩形的一组邻边
的长即可.由△ABO和△ADO的周长之差为2 cm,
可得AB-AD=2 cm.∵矩形的对角线相等且互相平
分,且两条对角线长之和为20 cm,∴AO=5 cm.又
△ABO和△ADO的周长之和为34 cm,可得AD+AB
=14 cm,从而求出AD,AB的长,故可求出矩形的
周长和面积.导引:知3-讲由题意得
AC=BD,AO=CO= AC,OB=OD= BD,
∴OA=OB=OC=OD= AC.
∵AC+BD=20 cm,∴AC=BD=10 cm,AO=5 cm.
∵AB+AO+OB+AD+AO+DO=34 cm,
∴AB+AD+2AO+BD=34 cm,∴AB+AD=14 cm.
又∵(AB+AO+BO)-(AD+AO+DO)=2 cm,
∴AB-AD=2 cm,∴AB=8 cm,AD=6 cm,
∴矩形ABCD的周长为2×(8+6)=28(cm),
矩形ABCD的面积为8×6=48(cm2).解: 本题利用了矩形的性质“对角线相等且互相平
分”.同时,在矩形被对角线分得的四个三角形中,
相邻两个三角形的周长之差等于邻边长之差.知3-讲1 如图,在矩形ABCD中,对角线AC与BD相交于点O试找出图中相等的线段与相等的角.
2 如图,矩形ABCD的两条对角线相交于点O,∠AOD=120°.求证AC=2AB.知3-练知3-练3 如图,EF过矩形ABCD对角线的交点O,且分别交AB,CD于E,F,那么阴影部分的面积是矩形ABCD的( )
A. B.
C. D. 1.矩形是特殊的平行四边形,具有平行四边形的所有性
质,它的特殊性就是四个角都是直角和对角线相等.
2.矩形的对角线将矩形分为两对全等的等腰三角形.
在解题的时候常用等腰三角形的性质.
3.矩形既是中心对称图形又是轴对称图形,有两条对称
轴.1.必做: 完成教材P100练习T3,P101练习T2-3
2.补充: 请完成练习册剩余部分习题
矩形的边角性质
矩形的对角线性质2课时流程逐点
导讲练课堂小结作业提升什么是平行四边形?
平行四边形都有哪些性质?1知识点矩形的定义知1-导 如图,用四根木条做一个平行四边形的活动木框,
将其直立在地面上并轻轻推动,你会发现 什么?知1-讲定义:有一个角是直角的平行四边形叫做矩形.
注意:
(1)由矩形的定义知,矩形一定是平行四边形,但平
行四边形不一定是矩形.
(2)矩形必须具备两个条件:
①它是一个平行四边形;
②它有一个角是直角,这两个条件缺一不可. 知1-讲例1 下列说法正确的是( )
A.平行四边形是矩形
B.矩形不一定是平行四边形
C.有一个角是直角的四边形是矩形
D.平行四边形具有的性质矩形都具有D1 如图,四边形ABCD的对角线互相平分,要使它
变为矩形,需要添加的条件是( )
A.AB=CD
B.AD=BC
C.∠AOB=45°
D.∠ABC=90°知1-练2 如图,小贤为了体验四边形的不稳定性,将四根木条用钉子钉成一个矩形框架ABCD,B与D两点之间用一根橡皮筋拉直固定,然后向右扭动框架,观察所得四边形的变化,下列判断错误的是( )
A.四边形ABCD由矩形变为平行四边形
B.BD的长度增大
C.四边形ABCD的面积不变
D.四边形ABCD的周长不变知1-练2知识点矩形的边角性质知2-讲性质:
(1)矩形的四个角都是直角.
(2)矩形具有平行四边形的所有性质.
(3)矩形是轴对称图形,如图所示, 邻边不相等的矩
形有两条对称轴.知2-讲要点精析:
(1)从边看:对边平行且相等;
(2)从角看:四个角都是直角;
(3)对称性:是中心对称图形,也是轴对称图形,邻边
不相等的矩形有两条对称轴;
(4)面积:
矩形的面积=长×宽;
矩形的面积=被对角线分成的四个等面积的小三角
形面积之和,
注:这四个小三角形是两对全等的等腰三角形.知2-讲例2 如图,在矩形ABCD中,AB =3,BC =4,BE⊥AC,垂足为点 E. 试求BE 的长.在矩形ABCD中, ∠ABC = 90°,解:又∵S△ABC1 如图,在矩形ABCD中,E是AD边上的一点.试说明△BCE的面积与矩形ABCD的面积之间的关系.知2-练知2-练2 如图,在矩形ABCD中,AB=6 cm,点E,F分别是边BC,AD上一点,将矩形ABCD沿EF折叠,使点C,D分别落在点C′,D′处.若C′E⊥AD,则EF的长为________cm.知2-练3 如图,点E是矩形ABCD的边AD延长线上的一点,且AD=DE,连结BE交CD于点O,连结AO,下列结论中不正确的是( )
A.△AOB≌△BOC
B.△BOC≌△EOD
C.△AOD≌△EOD
D.△AOD≌△BOC3知识点矩形的对角线性质知3-讲矩形的性质定理 2 矩形的对角线相等.知3-讲例3 如图,矩形ABCD被两条对角线分成四个小三角形, 如果四个小三角形周长的和是86 cm, 矩形的对角线长是13 cm,那么该矩形的周长是多少?∵△AOB、△BOC、△COD和△AOD四个小三角
形周长的和为86 cm.
∴AB+BC+CD+DA+2(OA+OB+OC+OD)
=AB+BC+CD+DA+2(AC+BD)
=86.
又∵AC=BD=13(矩形的对角线相等),
∴AB+BC+CD+DA=86-2(AC+BD)
=86-4×13=34(cm),
即矩形ABCD的周长等于34 cm.解:知3-讲知3-讲例4 如图,在矩形ABCD中,对角线AC与BD相交于点O,AE垂直且平分线段BO,垂足为点E,BD=15 cm.
求AC、AB的长.∵四边形ABCD是矩形,
∴AC=BD=15(矩形的
对角线相等),
∴AO= AC=7. 5.
∵AE垂直平分BO,
∴AB=AO=7. 5.
即AC的长为15 cm,AB的长为7. 5 cm.解:知3-讲例5 如图,在矩形ABCD(AB>AD)中,△AOB与△AOD的周长的差为2 cm,和为34 cm,两条对角线长的和为20 cm,求矩形的周长和面积.知3-讲要求矩形的周长和面积,只需求出矩形的一组邻边
的长即可.由△ABO和△ADO的周长之差为2 cm,
可得AB-AD=2 cm.∵矩形的对角线相等且互相平
分,且两条对角线长之和为20 cm,∴AO=5 cm.又
△ABO和△ADO的周长之和为34 cm,可得AD+AB
=14 cm,从而求出AD,AB的长,故可求出矩形的
周长和面积.导引:知3-讲由题意得
AC=BD,AO=CO= AC,OB=OD= BD,
∴OA=OB=OC=OD= AC.
∵AC+BD=20 cm,∴AC=BD=10 cm,AO=5 cm.
∵AB+AO+OB+AD+AO+DO=34 cm,
∴AB+AD+2AO+BD=34 cm,∴AB+AD=14 cm.
又∵(AB+AO+BO)-(AD+AO+DO)=2 cm,
∴AB-AD=2 cm,∴AB=8 cm,AD=6 cm,
∴矩形ABCD的周长为2×(8+6)=28(cm),
矩形ABCD的面积为8×6=48(cm2).解: 本题利用了矩形的性质“对角线相等且互相平
分”.同时,在矩形被对角线分得的四个三角形中,
相邻两个三角形的周长之差等于邻边长之差.知3-讲1 如图,在矩形ABCD中,对角线AC与BD相交于点O试找出图中相等的线段与相等的角.
2 如图,矩形ABCD的两条对角线相交于点O,∠AOD=120°.求证AC=2AB.知3-练知3-练3 如图,EF过矩形ABCD对角线的交点O,且分别交AB,CD于E,F,那么阴影部分的面积是矩形ABCD的( )
A. B.
C. D. 1.矩形是特殊的平行四边形,具有平行四边形的所有性
质,它的特殊性就是四个角都是直角和对角线相等.
2.矩形的对角线将矩形分为两对全等的等腰三角形.
在解题的时候常用等腰三角形的性质.
3.矩形既是中心对称图形又是轴对称图形,有两条对称
轴.1.必做: 完成教材P100练习T3,P101练习T2-3
2.补充: 请完成练习册剩余部分习题
