18.1.2 平行四边形的对角线性质 课件
文档属性
| 名称 | 18.1.2 平行四边形的对角线性质 课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-01-04 00:00:00 | ||
图片预览










文档简介
课件35张PPT。18.1.2 平行四边形的对角线性质1课堂讲解平行四边形的性质——对角线互相平分
平行四边形的面积2课时流程逐点
导讲练课堂小结作业提升1. 平行四边形的定义是什么?
2. 平行四边形的边、角有哪些性质?复习回顾1知识点平行四边形的性质——对角线互相平分 ABCD是一个中心对称图形,对角线的交
点O就是对称中心,有 OA = OC, OB = OD.
由此可得:
平行四边形的性质定理3 平行四边形的对角
线互相平分.知1-导知1-讲对角线的性质:平行四边形的对角线互相平分.
数学表达式:如图,∵四边形ABCD是
平行四边形,对角线AC,BD相交于点O,
∴OA=OC,OB=OD.
拓展:
(1)平行四边形的两条对角线把它分割成四个面积相等的三
角形;
数学表达式:
如图,∵四边形ABCD是平行四边形,对角线AC,BD
相交于点O,∴S△ABO=S△BCO=S△CDO=S△ADO.知1-讲(2)若一条直线过平行四边形两条对角线的交点,则该
直线平分平行四边形的周长和面积.
数学表达式:如图,∵直线EF过平
行四边形ABCD两对角线的交点O,
∴AE+AB+BF=FC+CD+DE
= (AB+BC+CD+DA),
S四边形ABFE=S四边形FCDE=
知1-讲如图, ABCD的对角线AC和BD相交于点O,△AOB的周长为15,AB = 6,那么对角线AC
与BD的和是多少?在 ABCD中,
∵AB = 6, AO +BO +AB = 15,
∴AO+BO =15-6 =9.
又∵AO =OC, BO =OD
(平行四边形的对角线互相平分),
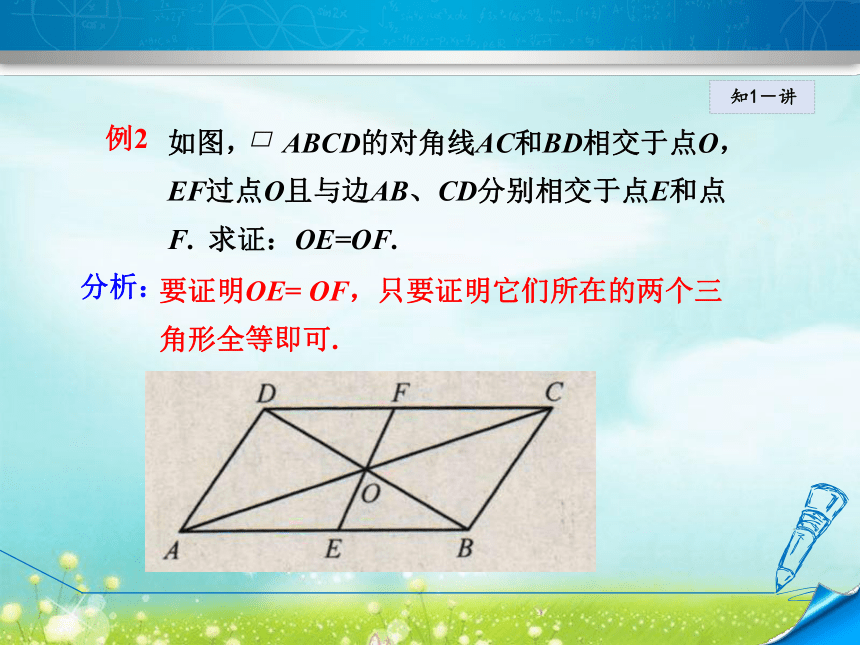
∴AC+BD=2AO+2BO= 2(AO+ BO) =2×9=18.证明:例1 知1-讲如图, ABCD的对角线AC和BD相交于点O,EF过点O且与边AB、CD分别相交于点E和点
F. 求证:OE=OF.要证明OE= OF,只要证明它们所在的两个三
角形全等即可.分析:例2 知1-讲∵四边形ABCD是平行四边形,
∴OB=OD(平行四边形的对角线互相平分).
又∵AB // DC ,
∴∠EBO =∠FDO.
又∵∠BOE =∠DOF,
∴△BEO≌△DFO.
∴OE = OF.解:知1-讲例3 由平行四边形对边相等知,
2AB+2BC=60,所以AB
+BC=30.又由△AOB的周
长比△BOC的周长长8,知
AB-BC=8,联立以上两
式,即可求出各边长.导引:如图,已知 ABCD的周长是60,对角线AC,BD
相交于点O.若△AOB的周长比△BOC的周长长8,求这个平行四边形各边的长.知1-讲∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,AB=CD,AD=BC.
∵AB+BC+CD+DA=60,
OA+AB+OB-(OB+BC+OC)=8,
∴AB+BC=30,AB-BC=8.
∴AB=CD=19,BC=AD=11,
即这个平行四边形各边长分别为19,11,19,11.解:知1-讲 在应用平行四边形的性质时,我们应从三个方
面去考虑:从边、角、对角线看它们的性质;解本
例时,我们从“平行四边形的对角线互相平分”中
得出“平行四边形被它的两条对角线分成四个小三
角形,相邻两个三角形的周长之差等于平行四边形
的两邻边之差”;熟记这些结论,能为计算带来很
多方便.知1-讲例4 平行四边形的性质提供了边的
平行与相等,角的相等与互补,
对角线的平分,当所要证明的
结论中的线段在对角线上时,
往往利用平行四边形的对角线互相平分这一性质.
因此本例要证对角线上的AE=CF,可考虑利用对
角线互相平分这一性质,先连接BD交AC于O,再
进行证明.导引:如图,已知?ABCD与?EBFD的顶点A、E、F、C在一条直线上,求证:AE=CF.知1-讲如图,连接BD交AC于O.
∵四边形ABCD是平行四边形,
∴OA=OC(平行四边形的对角线互相平分).
∵四边形EBFD是平行四边形,
∴OE=OF(平行四边形的对角线互相平分),
∴AE=CF(等式的性质).证明:知1-讲 本例易受全等三角形思维定式的影响.欲证的
两线段相等且又属于不同的三角形,习惯上就联想
到证这两个三角形全等,这样虽然能达到证明的目
的,却忽视了平行四边形的特有的性质,易走弯路.
因此在解决平行四边形的有关问题中,应注意运用
平行四边形的性质.知1-练如图, ABCD的对角线AC、BD相交于点O,
指出图中各对相等的线段知1-练如图,在 ABCD中,O是对角线AC、BD的交点,BE⊥AC, DF⊥AC, 垂足分别为E、F. 求证:OE= OF.知1-练 如图,已知 ABCD的对角线AC,
BD相交于点O,则下列说法一定正确的是( )
A.AO=OD
B.AO⊥OD
C.AO=OC
D.AO⊥AB知1-练4 如图,在平行四边形ABCD中,AB=3 cm,BC=5 cm,对角线AC,BD相交于点O,则OA的取值范围是( )
A.2 cm<OA<5 cm
B.2 cm<OA<8 cm
C.1 cm<OA<4 cm
D.3 cm<OA<8 cm知1-练5 如图,已知 ABCD的对角线AC与BD相交于点O,AB⊥AC. 若AB=4,AC=6,则BD的长是( )
A.8
B.9
C.10
D.11知1-练6 如图,在 ABCD中,对角线AC与BD交于点O,AE⊥BD于E,CF⊥BD于F,则图中全等的三角
形共有( )
A.7对
B.6对
C.5对
D.4对知1-练7 如图,已知 ABCD的对角线AC与BD相交于O,OE⊥BD于O交BC于E,连接DE,若△CED的周长是21 cm,则 ABCD的周长是________.2知识点平行四边形的面积知2-讲1.面积公式:平行四边形的面积=底×高(底为平行四边
形的任意一条边,高为这条边与其对边间的距离);
2.等底等高的平行四边形的面积相等.
要点精析:
(1)求面积时,底和高一定要对应,必须是底边上的高;
(2)等底等高的平行四边形与三角形面积间的关系:三角
形面积等于与它等底等高的平行四边形面积的一半.拓展:
(1)两等底平行四边形(三角形)面积的比等于它们高
的比;
(2)两等高平行四边形(三角形)面积的比等于它们底
的比.
3.根据平行四边形的两组对边相等,可知平行四边
形的周长等于两邻边和的2倍.知2-讲 如图,在 ABCD中,DE平分∠ADC,
AD=6,BE=2,则 ABCD的周长是________.例5 知2-讲20求 ABCD的周长,已知一条边AD=6,只需求出
AD的邻边AB或CD的长即可.
∵四边形ABCD是平行四边形,AD=6,BE=2,
∴AD=BC=6,∴EC=BC-BE=6-2=4,
∵ AD∥BC,∠ADE=∠DEC.
∵DE平分∠ADC,∠ADE=∠EDC.
∴∠EDC=∠DEC. ∴DC=EC=4.
∴ ABCD的周长是2×(4+6)=20.导引:知2-讲 如图,在 ABCD中,AB=4,BC=6,
∠B=30°,则此平行四边形的面积是( )
A.6
B.12
C.18
D.24例6 知2-讲B过点A作AE⊥BC于E,根据含30°角的直角三角形
的性质:在直角三角形中,30°角所对的直角边等
于斜边的一半可求出AE的长,利用平行四边形的面
积公式即可求出其面积.
如图,过点A作AE⊥BC于E,
∵在直角三角形ABE中,
∠B=30°,
∴AE= ×AB= ×4=2.
∴平行四边形ABCD的面积=BC·AE=6×2=12.导引:知2-讲知2-讲 求平行四边形的面积时,根据平行四边形的面
积公式,要知道平行四边形的一边长及这边上的高.
平行四边形的高不一定是过顶点的垂线段,因为平
行线间的距离处处相等.如图,在 ABCD中,对角线AC=21cm,
BC⊥AC=6,垂足为点E,且BE=5cm,AD=7cm.
求AD和BC之间的距离.例7 知2-讲设AD和BC之间的距离为x,则 ABCD的面积等
于AD·x.
∵
∴AD·x=AC·BE,
即7x=21×5,∴x=15(cm).
即AD和BC之间的距离为15cm.解:1 将一张平行四边形的纸片折一次,使得折痕平分这个平行四边形的面积.则这样的折纸方法有( )
A.1种 B.2种
C.4种 D.无数种知2-练2 如图, 在平行四边形ABCD中,点A1,A2,A3,A4和C1,C2,C3,C4分别是AB和CD的五等分点,点B1,B2和D1,D2分别是BC和DA的三等分点,已知四边形A4B2C4D2的面积为1,则平行四边形ABCD的面积为( )
A.2 B.
C. D.15知2-练知2-练3 如图,过 ABCD的对角线BD上一点M分别作平行四边形两边的平行线EF与GH,那么图中的 AEMG
的面积S1与 HCFM的面积S2的大小关系是( )
A.S1>S2
B.S1<S2
C.S1=S2
D.2S1=S21.平行四边形的性质:
(1)边:平行四边形的对边相等.
(2)角:平行四边形的对角相等.
(3)对角线:平行四边形的对角线相等.
2.平行四边形的面积:
(1)面积公式:平行四边形的面积=底×高(底为平行四
边形的任意一条边,高为这条边与其对边间的距离);
(2)等底等高的平行四边形的面积相等.必做: 完成教材P78练习T3, P80练习T1-3
补充: 请完成练习册剩余部分习题
平行四边形的面积2课时流程逐点
导讲练课堂小结作业提升1. 平行四边形的定义是什么?
2. 平行四边形的边、角有哪些性质?复习回顾1知识点平行四边形的性质——对角线互相平分 ABCD是一个中心对称图形,对角线的交
点O就是对称中心,有 OA = OC, OB = OD.
由此可得:
平行四边形的性质定理3 平行四边形的对角
线互相平分.知1-导知1-讲对角线的性质:平行四边形的对角线互相平分.
数学表达式:如图,∵四边形ABCD是
平行四边形,对角线AC,BD相交于点O,
∴OA=OC,OB=OD.
拓展:
(1)平行四边形的两条对角线把它分割成四个面积相等的三
角形;
数学表达式:
如图,∵四边形ABCD是平行四边形,对角线AC,BD
相交于点O,∴S△ABO=S△BCO=S△CDO=S△ADO.知1-讲(2)若一条直线过平行四边形两条对角线的交点,则该
直线平分平行四边形的周长和面积.
数学表达式:如图,∵直线EF过平
行四边形ABCD两对角线的交点O,
∴AE+AB+BF=FC+CD+DE
= (AB+BC+CD+DA),
S四边形ABFE=S四边形FCDE=
知1-讲如图, ABCD的对角线AC和BD相交于点O,△AOB的周长为15,AB = 6,那么对角线AC
与BD的和是多少?在 ABCD中,
∵AB = 6, AO +BO +AB = 15,
∴AO+BO =15-6 =9.
又∵AO =OC, BO =OD
(平行四边形的对角线互相平分),
∴AC+BD=2AO+2BO= 2(AO+ BO) =2×9=18.证明:例1 知1-讲如图, ABCD的对角线AC和BD相交于点O,EF过点O且与边AB、CD分别相交于点E和点
F. 求证:OE=OF.要证明OE= OF,只要证明它们所在的两个三
角形全等即可.分析:例2 知1-讲∵四边形ABCD是平行四边形,
∴OB=OD(平行四边形的对角线互相平分).
又∵AB // DC ,
∴∠EBO =∠FDO.
又∵∠BOE =∠DOF,
∴△BEO≌△DFO.
∴OE = OF.解:知1-讲例3 由平行四边形对边相等知,
2AB+2BC=60,所以AB
+BC=30.又由△AOB的周
长比△BOC的周长长8,知
AB-BC=8,联立以上两
式,即可求出各边长.导引:如图,已知 ABCD的周长是60,对角线AC,BD
相交于点O.若△AOB的周长比△BOC的周长长8,求这个平行四边形各边的长.知1-讲∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,AB=CD,AD=BC.
∵AB+BC+CD+DA=60,
OA+AB+OB-(OB+BC+OC)=8,
∴AB+BC=30,AB-BC=8.
∴AB=CD=19,BC=AD=11,
即这个平行四边形各边长分别为19,11,19,11.解:知1-讲 在应用平行四边形的性质时,我们应从三个方
面去考虑:从边、角、对角线看它们的性质;解本
例时,我们从“平行四边形的对角线互相平分”中
得出“平行四边形被它的两条对角线分成四个小三
角形,相邻两个三角形的周长之差等于平行四边形
的两邻边之差”;熟记这些结论,能为计算带来很
多方便.知1-讲例4 平行四边形的性质提供了边的
平行与相等,角的相等与互补,
对角线的平分,当所要证明的
结论中的线段在对角线上时,
往往利用平行四边形的对角线互相平分这一性质.
因此本例要证对角线上的AE=CF,可考虑利用对
角线互相平分这一性质,先连接BD交AC于O,再
进行证明.导引:如图,已知?ABCD与?EBFD的顶点A、E、F、C在一条直线上,求证:AE=CF.知1-讲如图,连接BD交AC于O.
∵四边形ABCD是平行四边形,
∴OA=OC(平行四边形的对角线互相平分).
∵四边形EBFD是平行四边形,
∴OE=OF(平行四边形的对角线互相平分),
∴AE=CF(等式的性质).证明:知1-讲 本例易受全等三角形思维定式的影响.欲证的
两线段相等且又属于不同的三角形,习惯上就联想
到证这两个三角形全等,这样虽然能达到证明的目
的,却忽视了平行四边形的特有的性质,易走弯路.
因此在解决平行四边形的有关问题中,应注意运用
平行四边形的性质.知1-练如图, ABCD的对角线AC、BD相交于点O,
指出图中各对相等的线段知1-练如图,在 ABCD中,O是对角线AC、BD的交点,BE⊥AC, DF⊥AC, 垂足分别为E、F. 求证:OE= OF.知1-练 如图,已知 ABCD的对角线AC,
BD相交于点O,则下列说法一定正确的是( )
A.AO=OD
B.AO⊥OD
C.AO=OC
D.AO⊥AB知1-练4 如图,在平行四边形ABCD中,AB=3 cm,BC=5 cm,对角线AC,BD相交于点O,则OA的取值范围是( )
A.2 cm<OA<5 cm
B.2 cm<OA<8 cm
C.1 cm<OA<4 cm
D.3 cm<OA<8 cm知1-练5 如图,已知 ABCD的对角线AC与BD相交于点O,AB⊥AC. 若AB=4,AC=6,则BD的长是( )
A.8
B.9
C.10
D.11知1-练6 如图,在 ABCD中,对角线AC与BD交于点O,AE⊥BD于E,CF⊥BD于F,则图中全等的三角
形共有( )
A.7对
B.6对
C.5对
D.4对知1-练7 如图,已知 ABCD的对角线AC与BD相交于O,OE⊥BD于O交BC于E,连接DE,若△CED的周长是21 cm,则 ABCD的周长是________.2知识点平行四边形的面积知2-讲1.面积公式:平行四边形的面积=底×高(底为平行四边
形的任意一条边,高为这条边与其对边间的距离);
2.等底等高的平行四边形的面积相等.
要点精析:
(1)求面积时,底和高一定要对应,必须是底边上的高;
(2)等底等高的平行四边形与三角形面积间的关系:三角
形面积等于与它等底等高的平行四边形面积的一半.拓展:
(1)两等底平行四边形(三角形)面积的比等于它们高
的比;
(2)两等高平行四边形(三角形)面积的比等于它们底
的比.
3.根据平行四边形的两组对边相等,可知平行四边
形的周长等于两邻边和的2倍.知2-讲 如图,在 ABCD中,DE平分∠ADC,
AD=6,BE=2,则 ABCD的周长是________.例5 知2-讲20求 ABCD的周长,已知一条边AD=6,只需求出
AD的邻边AB或CD的长即可.
∵四边形ABCD是平行四边形,AD=6,BE=2,
∴AD=BC=6,∴EC=BC-BE=6-2=4,
∵ AD∥BC,∠ADE=∠DEC.
∵DE平分∠ADC,∠ADE=∠EDC.
∴∠EDC=∠DEC. ∴DC=EC=4.
∴ ABCD的周长是2×(4+6)=20.导引:知2-讲 如图,在 ABCD中,AB=4,BC=6,
∠B=30°,则此平行四边形的面积是( )
A.6
B.12
C.18
D.24例6 知2-讲B过点A作AE⊥BC于E,根据含30°角的直角三角形
的性质:在直角三角形中,30°角所对的直角边等
于斜边的一半可求出AE的长,利用平行四边形的面
积公式即可求出其面积.
如图,过点A作AE⊥BC于E,
∵在直角三角形ABE中,
∠B=30°,
∴AE= ×AB= ×4=2.
∴平行四边形ABCD的面积=BC·AE=6×2=12.导引:知2-讲知2-讲 求平行四边形的面积时,根据平行四边形的面
积公式,要知道平行四边形的一边长及这边上的高.
平行四边形的高不一定是过顶点的垂线段,因为平
行线间的距离处处相等.如图,在 ABCD中,对角线AC=21cm,
BC⊥AC=6,垂足为点E,且BE=5cm,AD=7cm.
求AD和BC之间的距离.例7 知2-讲设AD和BC之间的距离为x,则 ABCD的面积等
于AD·x.
∵
∴AD·x=AC·BE,
即7x=21×5,∴x=15(cm).
即AD和BC之间的距离为15cm.解:1 将一张平行四边形的纸片折一次,使得折痕平分这个平行四边形的面积.则这样的折纸方法有( )
A.1种 B.2种
C.4种 D.无数种知2-练2 如图, 在平行四边形ABCD中,点A1,A2,A3,A4和C1,C2,C3,C4分别是AB和CD的五等分点,点B1,B2和D1,D2分别是BC和DA的三等分点,已知四边形A4B2C4D2的面积为1,则平行四边形ABCD的面积为( )
A.2 B.
C. D.15知2-练知2-练3 如图,过 ABCD的对角线BD上一点M分别作平行四边形两边的平行线EF与GH,那么图中的 AEMG
的面积S1与 HCFM的面积S2的大小关系是( )
A.S1>S2
B.S1<S2
C.S1=S2
D.2S1=S21.平行四边形的性质:
(1)边:平行四边形的对边相等.
(2)角:平行四边形的对角相等.
(3)对角线:平行四边形的对角线相等.
2.平行四边形的面积:
(1)面积公式:平行四边形的面积=底×高(底为平行四
边形的任意一条边,高为这条边与其对边间的距离);
(2)等底等高的平行四边形的面积相等.必做: 完成教材P78练习T3, P80练习T1-3
补充: 请完成练习册剩余部分习题
