6.2.1 由边的关系判定平行四边形课件
文档属性
| 名称 | 6.2.1 由边的关系判定平行四边形课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-01-05 00:00:00 | ||
图片预览










文档简介
课件30张PPT。6.2.1 由边的关系判定平行四边形6.2 平行四边形的判定1课堂讲解由两组对边关系判定平行四边形
由一组对边的关系判定平行四边形2课时流程逐点
导讲练课堂小结作业提升1.平行四边形的定义是什么?它有什么作用?
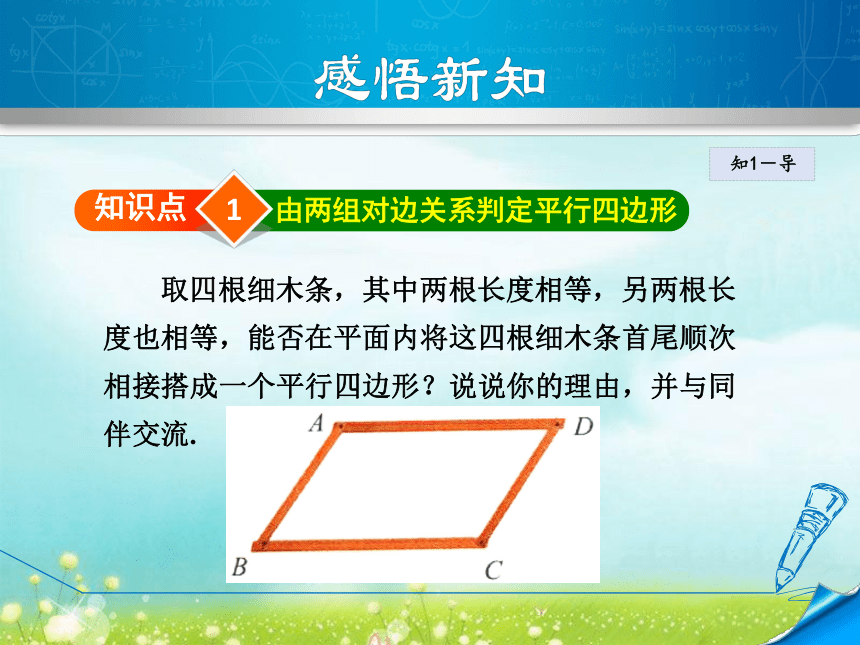
2.平行四边形的性质有哪些?复习回顾1知识点由两组对边关系判定平行四边形 取四根细木条,其中两根长度相等,另两根长
度也相等,能否在平面内将这四根细木条首尾顺次
相接搭成一个平行四边形?说说你的理由,并与同
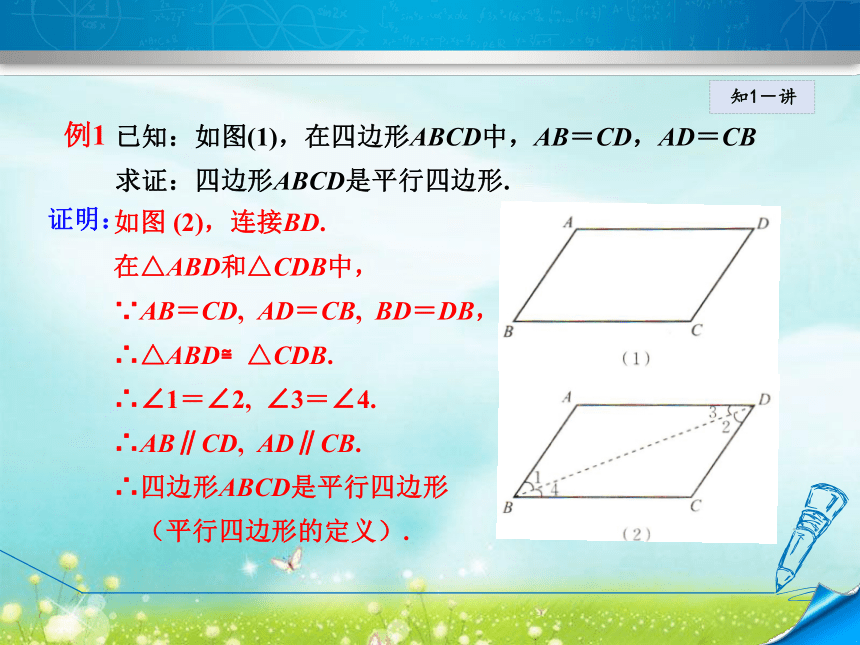
伴交流.知1-导定理 两组对边分别相等的四边形是平行四边形.归 纳知1-导知1-讲已知:如图(1),在四边形ABCD中,AB=CD,AD=CB
求证:四边形ABCD是平行四边形.如图 (2),连接BD.
在△ABD和△CDB中,
∵AB=CD, AD=CB, BD=DB,
∴△ABD≌△CDB.
∴∠1=∠2, ∠3=∠4.
∴AB∥CD, AD∥CB.
∴四边形ABCD是平行四边形
(平行四边形的定义).证明:例1 知1-讲两组对边分别相等的四边形是平行四边形;
数学表达式:
如图,∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形.知1-讲例2 如图,已知四边形ABCD是平行四边形,DE平分∠ADC,交CB的延长线于点E,BF平分∠ABC,交AD的延长线于点F.
求证:四边形BFDE是平行四边形.要证四边形BFDE是平行四
边形,根据平行四边形的定
义可证得DF∥BE,因此可
采用判定方法一即定义法,
只需证明DE∥FB即可.导引:知1-讲∵四边形ABCD是平行四边形,
∴∠ADC=∠ABC,AD∥CB. ∴DF∥BE.
∵DE平分∠ADC,BF平分∠ABC,
∴∠1=∠2=∠3=∠4.
∵AD∥BC,∴∠1=∠E. ∴∠E=∠3.
∴DE∥FB.
∴四边形BFDE是平行四边形(两组对边分别平
行的四边形是平行四边形).证明:知1-讲 平行四边形的定义是判定平行四边形的根本方
法,也是其他判定方法的基础.当题目中出现平行
的线段时,往往借助判定方法一来帮助我们对四边
形加以判断.总 结知1-讲例3 导引:由等边三角形的性质可以得到
线段相等,角相等,进而可以
通过全等三角形证明四边形
ADEF的两组对边分别相等,最
后根据两组对边分别相等的四
边形是平行四边形进行判定.如图,分别以△ABC的三边为一边,在BC的同侧作等边三角形ABD,等边三角形BCE,等边三角形ACF,连接DE,EF.
求证:四边形ADEF是平行四边形.知1-讲∵△ABD,△BCE,△ACF都为等边三角形,
∴DB=AB=AD,BE=BC,AC=AF,
∠DBA=60°,∠EBC=60°.
∴∠DBE=60°-∠EBA,∠ABC=60°-∠EBA.
∴∠DBE=∠ABC. ∴△DBE≌△ABC.
∴DE=AC.
又∵AC=AF,∴AF=DE. 同理可证:△ABC≌△FEC,
∴AB=FE. ∴FE=AD.
∴四边形ADEF是平行四边形.证明:知1-讲 根据等边三角形的性质可以得到线段相等,角
相等,进而通过证明三角形全等得到四边形ADEF
的两组对边分别相等,根据两组对边分别相等的四
边形是平行四边形得证.总 结知1-练1 四边形的四条边长分别是a,b,c,d,其中a,b为一组对边长,c,d为另一组对边长且a2+b2+c2+d2=2ab+2cd,则这个四边形是( )
A.任意四边形
B.平行四边形
C.对角线相等的四边形
D.对角线垂直的四边形知1-练2 小敏不慎将一块平行四边形玻璃打碎成如图所示的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,她带了两块碎玻璃,其编号应该是( )
A.①②
B.①④
C.③④
D.②③知1-练3 下列图形中,一定可以拼成平行四边形的是( )
A.两个等腰三角形
B.两个直角三角形
C.两个锐角三角形
D.两个全等三角形知1-练4 如图,点A是直线l外一点,在l上取两点B,C,连接AB,分别以A,C为圆心,BC,AB长为半径画弧,两弧交于点D,分别连接AD,CD,则四边形ABCD的形状是________.2知识点由一组对边的关系判定平行四边形知2-导议一议
(1)取两根长度相等的细木条,你能将它们摆放在一
张纸上,使得这两根细木条的四个端点恰好是一
个平行四边形的四个顶点吗?
(2)如果四边形有一组对边相等,那么还需要添加什
么条件,才能使它成为平行四边形?与同伴交流.定理 一组对边平行且相等的四边形是平行四边形.归 纳知2-导如图 (2),连接AC.
∵AB∥CD,∴∠BAC=∠DCA.
又∵AB=CD,AC=CA,
∴△ABC≌△CDA.
∴BC=DA.
∴四边形ABCD是平行四边形(两组对边分别相
等的四边形是平行 四边形).证明:知2-讲已知:如图(1),在四边形ABCD中,AB CD.
求证:四边形ABCD是平行四边形.例4 知2-讲一组对边平行且相等的四边形是平行四边形;
数学表达式:
如图,∵AB CD,
∴四边形ABCD是平行四边形.例5 知2-讲已知:如图,在 ABCD中,E, F分别为AD和CB的中点.
求证:四边形BFDE是平行四边形.
∵四边形ABCD是平行四边形,
∴AD=CB(平行四边形的对边相等),
AD∥CB(平行四边形的定义).
∵E,F分别是AD和CB的中点,
∴ED=FB,ED∥FB.
∴四边形DFDE是平行四边形(一组对边平行且
相等的四边形是平行四边形).证明:如图,在 ABCD中,点E,F分别为AB,CD上的点,且AE=CF,点M,N分别是BF,DE的中点.
求证:四边形ENFM是平行四边形.例6 知2-讲由 ABCD的性质得,
CD∥AB,CD=AB,
再根据题目反映的条件特
征两次证平行四边形均易
联想利用一组对边平行且
相等来分析证明.导引:∵四边形ABCD是平行四边形,
∴CD∥AB,CD=AB.
又∵CF=AE,∴CD-CF=AB-AE,即DF=EB.
∴四边形DEBF是平行四边形.
∴DE∥BF,DE=BF.
又∵点M,N分别为BF,DE的中点,
∴FM= BF,NE= DE.
∴NE=FM.
∴四边形ENFM为平行四边形(一组对边平行且相等
的四边形是平行四边形).证明:知2-讲知2-讲 在四边形中证明线段相等或平行时,可先判定
四边形是平行四边形,再利用平行四边形的性质解
决问题,最后利用已证结论去判定最终要判定的另
一个四边形是否是平行四边形.总 结1 如图,在 ABCD中,E,F分别是AB,CD的中点,连接DE,EF,BF,则图中平行四边形共有( )
A.2个
B.4个
C.6个
D.8个知2-练2 在四边形ABCD中,AD=BC,若四边形ABCD
是平行四边形,则还应满足( )
A.∠A+∠C=180°
B.∠B+∠D=180°
C.∠A+∠B=180°
D.∠A+∠D=180°知2-练知2-练3 如图,在 ABCD中,点E,F分别在AD,BC上,若要使四边形AFCE是平行四边形,可以添加的条件是
( )
①AF=CF;②AE=CE;③BF=DE;④AF∥CE
A.①或②
B.②或③
C.③或④
D.①或③有边判定四边形是平行四边形的方法有:
1.定义:两组对边分别平行的四边形是平行四边形.
2.两组对边分别相等的四边形是平行四边形.
3.一组对边平行且相等的四边形是平行四边形.1. 必做: 完成教材P142随堂练习T1-2,
习题6.3T1-4
2. 补充: 请完成练习册剩余部分习题
由一组对边的关系判定平行四边形2课时流程逐点
导讲练课堂小结作业提升1.平行四边形的定义是什么?它有什么作用?
2.平行四边形的性质有哪些?复习回顾1知识点由两组对边关系判定平行四边形 取四根细木条,其中两根长度相等,另两根长
度也相等,能否在平面内将这四根细木条首尾顺次
相接搭成一个平行四边形?说说你的理由,并与同
伴交流.知1-导定理 两组对边分别相等的四边形是平行四边形.归 纳知1-导知1-讲已知:如图(1),在四边形ABCD中,AB=CD,AD=CB
求证:四边形ABCD是平行四边形.如图 (2),连接BD.
在△ABD和△CDB中,
∵AB=CD, AD=CB, BD=DB,
∴△ABD≌△CDB.
∴∠1=∠2, ∠3=∠4.
∴AB∥CD, AD∥CB.
∴四边形ABCD是平行四边形
(平行四边形的定义).证明:例1 知1-讲两组对边分别相等的四边形是平行四边形;
数学表达式:
如图,∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形.知1-讲例2 如图,已知四边形ABCD是平行四边形,DE平分∠ADC,交CB的延长线于点E,BF平分∠ABC,交AD的延长线于点F.
求证:四边形BFDE是平行四边形.要证四边形BFDE是平行四
边形,根据平行四边形的定
义可证得DF∥BE,因此可
采用判定方法一即定义法,
只需证明DE∥FB即可.导引:知1-讲∵四边形ABCD是平行四边形,
∴∠ADC=∠ABC,AD∥CB. ∴DF∥BE.
∵DE平分∠ADC,BF平分∠ABC,
∴∠1=∠2=∠3=∠4.
∵AD∥BC,∴∠1=∠E. ∴∠E=∠3.
∴DE∥FB.
∴四边形BFDE是平行四边形(两组对边分别平
行的四边形是平行四边形).证明:知1-讲 平行四边形的定义是判定平行四边形的根本方
法,也是其他判定方法的基础.当题目中出现平行
的线段时,往往借助判定方法一来帮助我们对四边
形加以判断.总 结知1-讲例3 导引:由等边三角形的性质可以得到
线段相等,角相等,进而可以
通过全等三角形证明四边形
ADEF的两组对边分别相等,最
后根据两组对边分别相等的四
边形是平行四边形进行判定.如图,分别以△ABC的三边为一边,在BC的同侧作等边三角形ABD,等边三角形BCE,等边三角形ACF,连接DE,EF.
求证:四边形ADEF是平行四边形.知1-讲∵△ABD,△BCE,△ACF都为等边三角形,
∴DB=AB=AD,BE=BC,AC=AF,
∠DBA=60°,∠EBC=60°.
∴∠DBE=60°-∠EBA,∠ABC=60°-∠EBA.
∴∠DBE=∠ABC. ∴△DBE≌△ABC.
∴DE=AC.
又∵AC=AF,∴AF=DE. 同理可证:△ABC≌△FEC,
∴AB=FE. ∴FE=AD.
∴四边形ADEF是平行四边形.证明:知1-讲 根据等边三角形的性质可以得到线段相等,角
相等,进而通过证明三角形全等得到四边形ADEF
的两组对边分别相等,根据两组对边分别相等的四
边形是平行四边形得证.总 结知1-练1 四边形的四条边长分别是a,b,c,d,其中a,b为一组对边长,c,d为另一组对边长且a2+b2+c2+d2=2ab+2cd,则这个四边形是( )
A.任意四边形
B.平行四边形
C.对角线相等的四边形
D.对角线垂直的四边形知1-练2 小敏不慎将一块平行四边形玻璃打碎成如图所示的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,她带了两块碎玻璃,其编号应该是( )
A.①②
B.①④
C.③④
D.②③知1-练3 下列图形中,一定可以拼成平行四边形的是( )
A.两个等腰三角形
B.两个直角三角形
C.两个锐角三角形
D.两个全等三角形知1-练4 如图,点A是直线l外一点,在l上取两点B,C,连接AB,分别以A,C为圆心,BC,AB长为半径画弧,两弧交于点D,分别连接AD,CD,则四边形ABCD的形状是________.2知识点由一组对边的关系判定平行四边形知2-导议一议
(1)取两根长度相等的细木条,你能将它们摆放在一
张纸上,使得这两根细木条的四个端点恰好是一
个平行四边形的四个顶点吗?
(2)如果四边形有一组对边相等,那么还需要添加什
么条件,才能使它成为平行四边形?与同伴交流.定理 一组对边平行且相等的四边形是平行四边形.归 纳知2-导如图 (2),连接AC.
∵AB∥CD,∴∠BAC=∠DCA.
又∵AB=CD,AC=CA,
∴△ABC≌△CDA.
∴BC=DA.
∴四边形ABCD是平行四边形(两组对边分别相
等的四边形是平行 四边形).证明:知2-讲已知:如图(1),在四边形ABCD中,AB CD.
求证:四边形ABCD是平行四边形.例4 知2-讲一组对边平行且相等的四边形是平行四边形;
数学表达式:
如图,∵AB CD,
∴四边形ABCD是平行四边形.例5 知2-讲已知:如图,在 ABCD中,E, F分别为AD和CB的中点.
求证:四边形BFDE是平行四边形.
∵四边形ABCD是平行四边形,
∴AD=CB(平行四边形的对边相等),
AD∥CB(平行四边形的定义).
∵E,F分别是AD和CB的中点,
∴ED=FB,ED∥FB.
∴四边形DFDE是平行四边形(一组对边平行且
相等的四边形是平行四边形).证明:如图,在 ABCD中,点E,F分别为AB,CD上的点,且AE=CF,点M,N分别是BF,DE的中点.
求证:四边形ENFM是平行四边形.例6 知2-讲由 ABCD的性质得,
CD∥AB,CD=AB,
再根据题目反映的条件特
征两次证平行四边形均易
联想利用一组对边平行且
相等来分析证明.导引:∵四边形ABCD是平行四边形,
∴CD∥AB,CD=AB.
又∵CF=AE,∴CD-CF=AB-AE,即DF=EB.
∴四边形DEBF是平行四边形.
∴DE∥BF,DE=BF.
又∵点M,N分别为BF,DE的中点,
∴FM= BF,NE= DE.
∴NE=FM.
∴四边形ENFM为平行四边形(一组对边平行且相等
的四边形是平行四边形).证明:知2-讲知2-讲 在四边形中证明线段相等或平行时,可先判定
四边形是平行四边形,再利用平行四边形的性质解
决问题,最后利用已证结论去判定最终要判定的另
一个四边形是否是平行四边形.总 结1 如图,在 ABCD中,E,F分别是AB,CD的中点,连接DE,EF,BF,则图中平行四边形共有( )
A.2个
B.4个
C.6个
D.8个知2-练2 在四边形ABCD中,AD=BC,若四边形ABCD
是平行四边形,则还应满足( )
A.∠A+∠C=180°
B.∠B+∠D=180°
C.∠A+∠B=180°
D.∠A+∠D=180°知2-练知2-练3 如图,在 ABCD中,点E,F分别在AD,BC上,若要使四边形AFCE是平行四边形,可以添加的条件是
( )
①AF=CF;②AE=CE;③BF=DE;④AF∥CE
A.①或②
B.②或③
C.③或④
D.①或③有边判定四边形是平行四边形的方法有:
1.定义:两组对边分别平行的四边形是平行四边形.
2.两组对边分别相等的四边形是平行四边形.
3.一组对边平行且相等的四边形是平行四边形.1. 必做: 完成教材P142随堂练习T1-2,
习题6.3T1-4
2. 补充: 请完成练习册剩余部分习题
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
