6.4.1 多边形的内角和 课件

课件24张PPT。6.4.1 多边形的内角和6.4 多边形的内角和与外角和1课堂讲解多边形的内角和
正多边形的内角和2课时流程逐点
导讲练课堂小结作业提升三角形的内角和是多少？复习回顾(1)上图中广场中心的边缘是一个五边形，你能设法求出它的
五个内角的和吗？与同伴交流.
(2)小明、小亮分别利用下面的图形求出了五边形的五个内角
的和.你知道他们是怎样做的吗？你还有其他的方法吗？1知识点多边形的内角和知1－导想一想
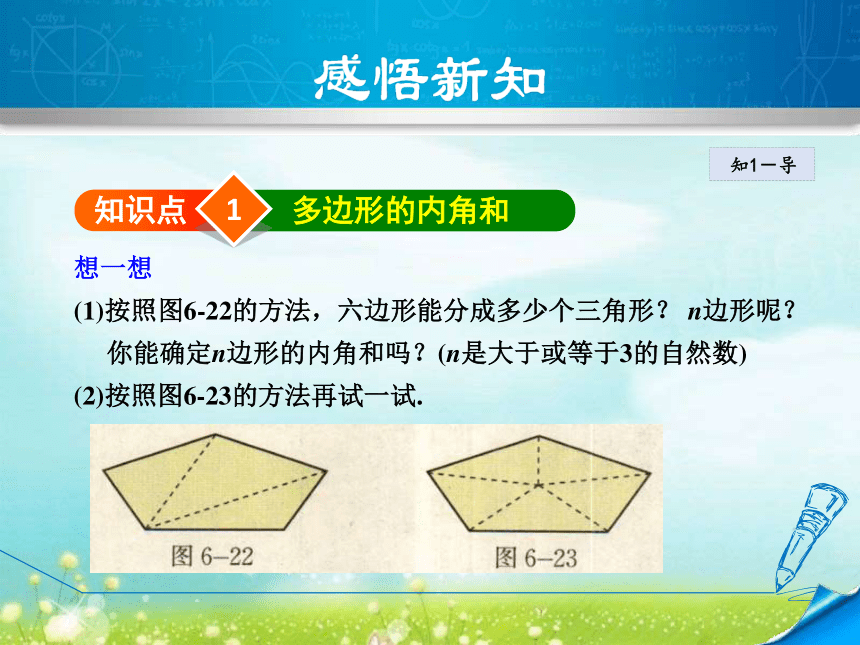
(1)按照图6-22的方法，六边形能分成多少个三角形？ n边形呢？
你能确定n边形的内角和吗？(n是大于或等于3的自然数)
(2)按照图6-23的方法再试一试.定理 n边形的内角和等于(n－2)·180°.知1－导知1－讲n边形的内角和等于(n－2)×180°(n≥3)．
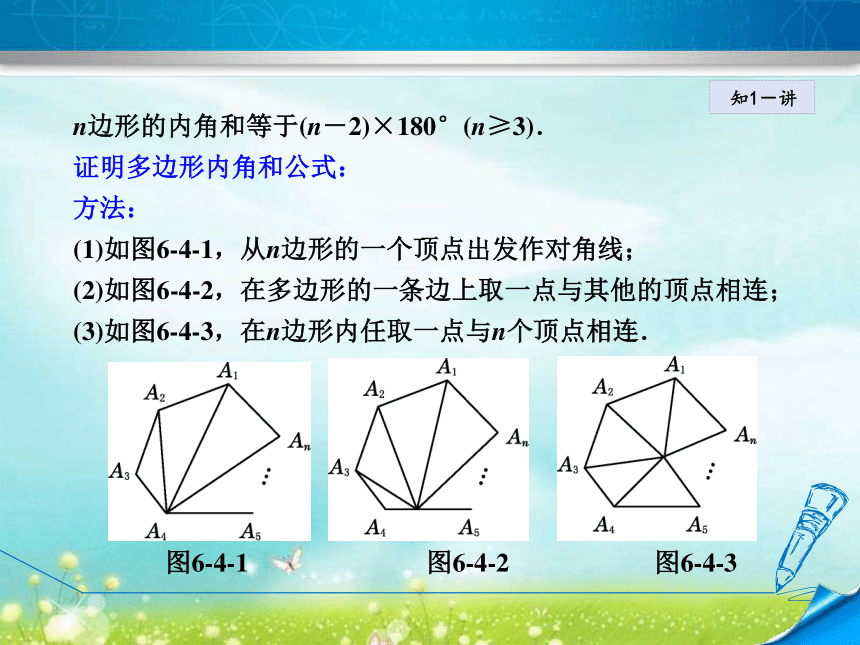
证明多边形内角和公式：
方法：
(1)如图6--4--1，从n边形的一个顶点出发作对角线；
(2)如图6--4--2，在多边形的一条边上取一点与其他的顶点相连；
(3)如图6--4--3，在n边形内任取一点与n个顶点相连．
图6--4--1 图6--4--2 图6--4--3知1－讲思路：把多边形内角和的问题转化为三角形内角和的
问题，即把n边形分成几个三角形，利用三角形内
角和定理推导．
拓展：多边形的内角和随边数的变化而变化，边数每
增加1，内角和就增加180°.知1－讲例1 ∵四边形的内角和为(4－2)×180°＝360°，
∴∠B＝360°－(∠A＋∠C＋∠D)
＝360°－280°
＝80°.导引： 在四边形ABCD中，若∠A＋∠C＋∠D＝280°，则∠B的度数是(　　)
A．80° B．90° C．170° D．20°A 已知边数求内角和，可直接代入内角和公式：
n边形内角和等于(n－2)×180°求解．知1－讲知1－讲例2 如图，在四边形ABCD中，∠A＋∠C=180°.∠B 与
∠D有怎样的关系?解：∵ ∠A＋∠B＋∠C＋∠D
＝(4－2)×180°＝360°，
∴∠B＋∠D
＝360°－(∠A＋∠C)
＝360°－180°
＝180°. 如果四边形一组对角互补，那么另一组
对角也互补.知1－讲知1－练1　一个多边形的内角和是360°，这个多边形是(　　)
A．三角形 　　　　　 B．四边形　　　
C．六边形 　　　　　 D．不能确定
2　下列角度中能成为某多边形的内角和的是(　　)
A．270°　　　　　　 B．560°
C．1 800°　　　　　　D．1 900°知1－练3　将一个n边形变成(n＋1)边形，内角和将(　　)
A．减少180° B．增加90°
C．增加180° D．增加360°
4　一个多边形除一个内角外其余内角的和为1 510°，则这个多边形对角线的条数是(　　)
A．27 B．35 C．44 D．542知识点正多边形的内角和知2－导想一想
正三角形（等边三角形）、正四边形（正方形）、
正五边形、正六边形、正八边形的内角分别是多少
度？知2－讲议一议
剪掉一张长方形纸片的一个角后，纸片还剩几个角？
这个多边形的内角和是多少度？与同伴交流.例3 知2－讲正n边形的每个内角的度数为 若一个多边形的内角和是1 260°，则这
个多边形的边数是________．设这个多边形的边数为n，由题意知，
(n－2)×180°＝1 260°，解得n＝9.导引：9(1)已知多边形的内角和求边数n的方法：根据多边形
内角和公式列方程：(n－2)×180°＝内角和，解
方程求出n，即得多边形的边数；
(2)已知正多边形每个内角的度数k求边数n的方法：
根据多边形内角和公式列方程：
(n－2)×180°＝kn，解方程求出n，即得多边形的
边数．知2－讲例4 知2－讲如图，求∠A＋∠ABC＋∠C＋∠D＋∠E＋∠F的度数．要求不规则图形的各个角的度数和，
就是想办法在不规则图形中找规则
图形，然后把不规则图形的角通过
已学的相关知识(本例中三角形外角
的性质)转移到规则的图形中去，即
把所求的六个角的和转移到四边形
BEFG中去．导引：知2－讲在四边形BEFG中，
∵∠EBG＝∠C＋∠D，
∠BGF＝∠A＋∠ABC，
∴∠A＋∠ABC＋∠C＋∠D＋∠E＋∠F
＝∠BGF＋∠EBG＋∠E＋∠F＝360°.解：(1)化不规则为规则是转化思想中一种常见的方法，
它主要经历了两步：第一步找规则图形，第二步
将不规则图形的角转化到规则图形中；关键是找
规则图形．这类题一般有不同的解法，如本例还
可以将四边形DEFH作为基础四边形，请读者自
己完成其解法．
(2)若图中没有已知的规则图形，则需通过作辅助线
构造规则图形．知2－讲1　一个多边形的每个内角均为120°，则这个多边形是(　　)
A．四边形 B．五边形
C．六边形 D．七边形
2　正八边形的每个内角都是(　　)
A．60° B．80°
C．100° D．135°知2－练(1)正n边形的每个内角都相等
(2)n边形的内角和与边数有关，每增加一条边，内角和就增加180°.
(3)利用公式，已知n边形的边数可求内角和，同样已
知内角和也可求边数．1. 必做: 完成教材P154随堂练习,
习题6.7T1-3
2. 补充: 请完成练习册剩余部分习题