1.1锐角三角函数(2)课件
图片预览




文档简介
课件16张PPT。1.1.2 锐角三角函数(二)义务教育教科书(北师)九年级数学下册
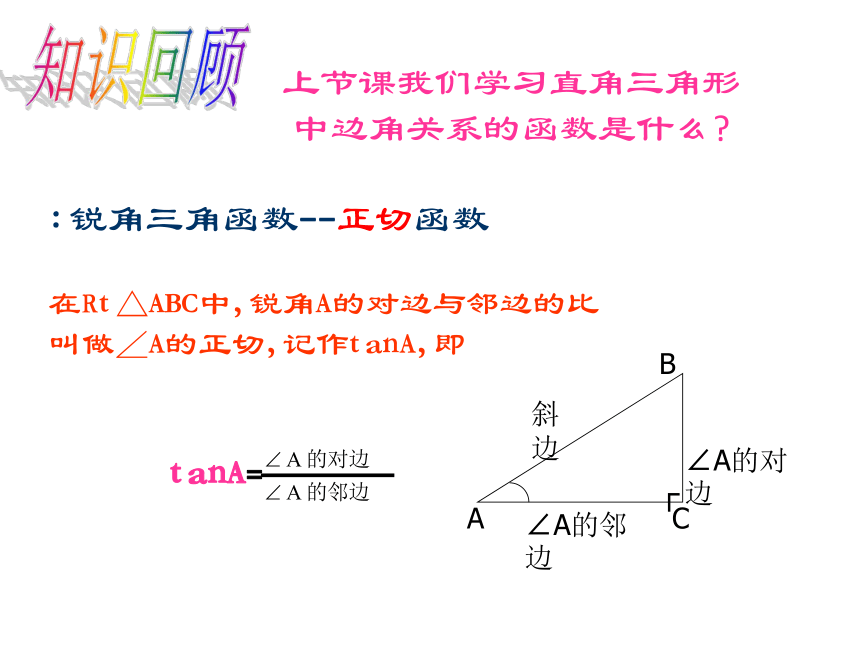
第一章 直角三角形的边角关系上节课我们学习直角三角形中边角关系的函数是什么?:锐角三角函数--正切函数在Rt△ABC中,锐角A的对边与邻边的比
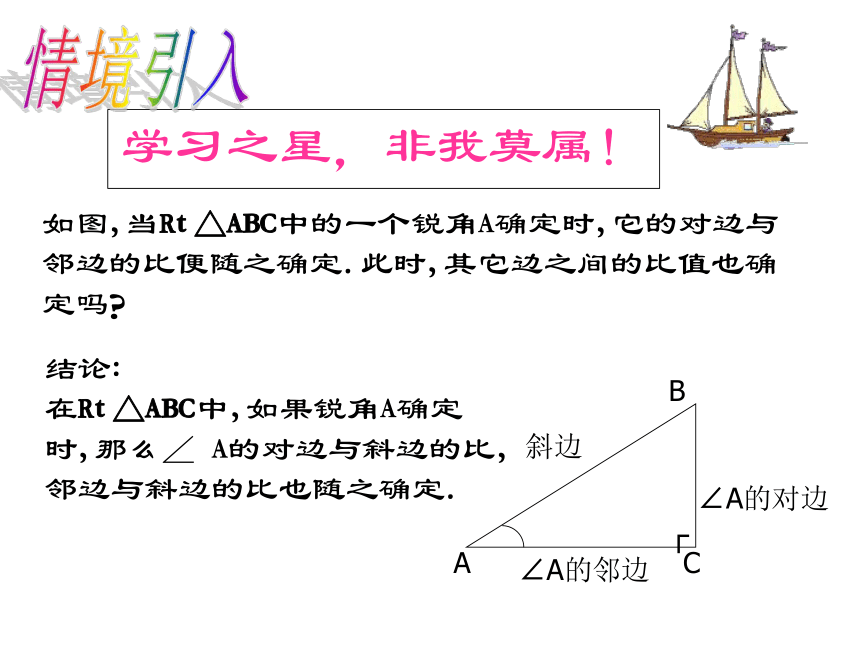
叫做∠A的正切,记作tanA,即知识回顾学习之星,非我莫属!如图,当Rt△ABC中的一个锐角A确定时,它的对边与邻边的比便随之确定.此时,其它边之间的比值也确定吗?结论:
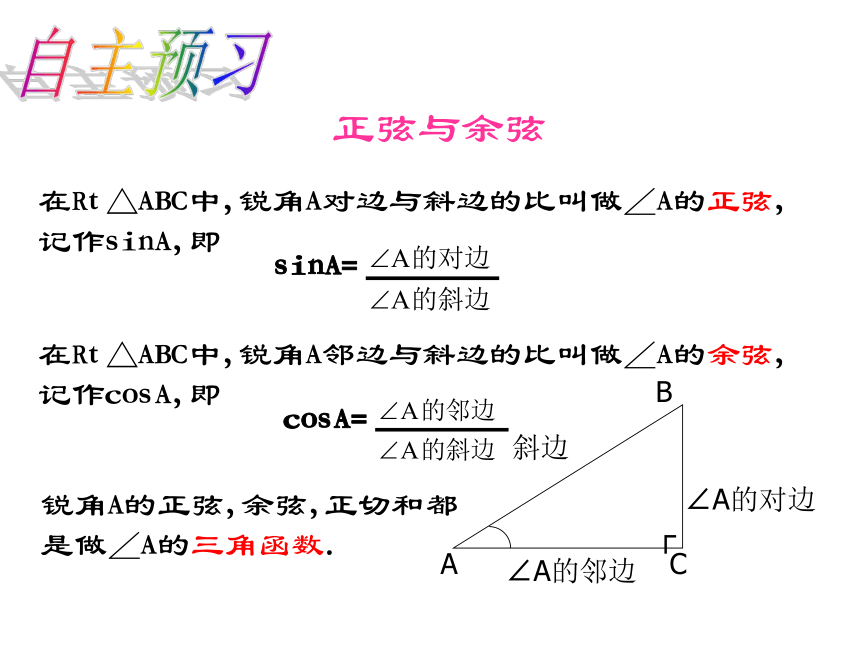
在Rt△ABC中,如果锐角A确定时,那么∠ A的对边与斜边的比,邻边与斜边的比也随之确定.情境引入正弦与余弦在Rt△ABC中,锐角A对边与斜边的比叫做∠A的正弦,记作sinA,即在Rt△ABC中,锐角A邻边与斜边的比叫做∠A的余弦,记作cosA,即锐角A的正弦,余弦,正切和都是做∠A的三角函数.自主预习我发现,我归纳结论:梯子的倾斜程度与sinA和cosA有关:
sinA越大,梯子越陡;cosA越小,梯子越陡.如图,梯子的倾斜程度与sinA和cosA有关吗?新知探究我会学,更会用例2 如图:在Rt△ABC,∠B=900,AC=200,sinA=0.6.
求:BC的长.老师期望:
请你求出cosA,tanA,sinC,cosC和tanC的值.你敢应战吗?定义中应该注意的几个问题:1.sinA,cosA,tanA, 是在直角三角形中定义的,∠A是锐角(注意数形结合,构造直角三角形).
2.sinA,cosA,tanA, 是一个完整的符号,表示∠A的正切,习惯省去“∠”号;
3.sinA,cosA,tanA,是一个比值.注意比的顺序,且sinA,cosA,tanA,均﹥0,无单位.
4.sinA,cosA,tanA, 的大小只与∠A的大小有关,而与直角三角形的边长无关.
5.角相等,则其三角函数值相等;两锐角的三角函数值相等,则这两个锐角相等.知识梳理看谁更灵活求:AB,sinB.如图:在Rt△ABC中,∠C=900,AC=10,
注意到这里cosA=sinB,其中有没有什么内在的关系?例题探究1.锐角三角函数定义:请思考:在Rt△ABC中,
sinA和cosB有什么关系? 你知道吗?我们学习的锐角三角函数(直角三角形边角关系的函数)共有以下三个。1.如图:在等腰△ABC中,AB=AC=5,BC=6.
求: sinB,cosB,tanB.求:△ABC的周长.2.在Rt△ABC中,∠C=900,BC=20,随堂练习3.如图,在Rt△ABC中,锐角A的对边和邻边同时扩大100倍,sinA的值( )
A.扩大100倍 B.缩小100倍
C.不变 D.不能确定4.已知∠A,∠B为锐角
(1)若∠A=∠B,则sinA sinB;
(2)若sinA=sinB,则∠A ∠B.随堂练习5.如图, ∠C=90°CD⊥AB.6.在上图中,若BD=6,CD=12.求cosA的值.随堂练习我会做,我会算7.如图,分别根据图(1)和图(2)求∠A的三个三角函数值.(2)BC=3,sinA= ,求AC和AB.求锐角三角函数时,运用勾股定理非常重要.随堂练习看谁做得更好!8.在Rt△ABC中,∠C=90°,AB=15,sinA= ,
求AC和BC.9.在等腰△ABC中,AB=AC=13,BC=10,
求sinB,cosB.随堂练习110. 如图,分别求∠α,∠β的正弦,余弦,和正切.11.在△ABC中,AB=5,BC=13,AD是BC边上的高,AD=4.求:CD,sinC.12.在Rt△ABC中,∠BCA=90°,CD是中线,BC=8,CD=5.
求sin∠ACD,cos∠ACD和tan∠ACD.13.在Rt△ABC中,∠C=90°,sinA和cosB有什么关系?随堂练习14. 在Rt△ABC中,∠C=90°.
(1)AC=25.AB=27.求sinA,cosA,tanA, 和sinB,cosB,tanB,.
(2)BC=3,sinA=0.6,求AC 和AB.
(3)AC=4,cosA=0.8,求BC.15.在梯形ABCD中,AD//BC,AB=DC=13,AD=8,BC=18.
求:sinB,cosB,tanB.驶向胜利的彼岸随堂练习
第一章 直角三角形的边角关系上节课我们学习直角三角形中边角关系的函数是什么?:锐角三角函数--正切函数在Rt△ABC中,锐角A的对边与邻边的比
叫做∠A的正切,记作tanA,即知识回顾学习之星,非我莫属!如图,当Rt△ABC中的一个锐角A确定时,它的对边与邻边的比便随之确定.此时,其它边之间的比值也确定吗?结论:
在Rt△ABC中,如果锐角A确定时,那么∠ A的对边与斜边的比,邻边与斜边的比也随之确定.情境引入正弦与余弦在Rt△ABC中,锐角A对边与斜边的比叫做∠A的正弦,记作sinA,即在Rt△ABC中,锐角A邻边与斜边的比叫做∠A的余弦,记作cosA,即锐角A的正弦,余弦,正切和都是做∠A的三角函数.自主预习我发现,我归纳结论:梯子的倾斜程度与sinA和cosA有关:
sinA越大,梯子越陡;cosA越小,梯子越陡.如图,梯子的倾斜程度与sinA和cosA有关吗?新知探究我会学,更会用例2 如图:在Rt△ABC,∠B=900,AC=200,sinA=0.6.
求:BC的长.老师期望:
请你求出cosA,tanA,sinC,cosC和tanC的值.你敢应战吗?定义中应该注意的几个问题:1.sinA,cosA,tanA, 是在直角三角形中定义的,∠A是锐角(注意数形结合,构造直角三角形).
2.sinA,cosA,tanA, 是一个完整的符号,表示∠A的正切,习惯省去“∠”号;
3.sinA,cosA,tanA,是一个比值.注意比的顺序,且sinA,cosA,tanA,均﹥0,无单位.
4.sinA,cosA,tanA, 的大小只与∠A的大小有关,而与直角三角形的边长无关.
5.角相等,则其三角函数值相等;两锐角的三角函数值相等,则这两个锐角相等.知识梳理看谁更灵活求:AB,sinB.如图:在Rt△ABC中,∠C=900,AC=10,
注意到这里cosA=sinB,其中有没有什么内在的关系?例题探究1.锐角三角函数定义:请思考:在Rt△ABC中,
sinA和cosB有什么关系? 你知道吗?我们学习的锐角三角函数(直角三角形边角关系的函数)共有以下三个。1.如图:在等腰△ABC中,AB=AC=5,BC=6.
求: sinB,cosB,tanB.求:△ABC的周长.2.在Rt△ABC中,∠C=900,BC=20,随堂练习3.如图,在Rt△ABC中,锐角A的对边和邻边同时扩大100倍,sinA的值( )
A.扩大100倍 B.缩小100倍
C.不变 D.不能确定4.已知∠A,∠B为锐角
(1)若∠A=∠B,则sinA sinB;
(2)若sinA=sinB,则∠A ∠B.随堂练习5.如图, ∠C=90°CD⊥AB.6.在上图中,若BD=6,CD=12.求cosA的值.随堂练习我会做,我会算7.如图,分别根据图(1)和图(2)求∠A的三个三角函数值.(2)BC=3,sinA= ,求AC和AB.求锐角三角函数时,运用勾股定理非常重要.随堂练习看谁做得更好!8.在Rt△ABC中,∠C=90°,AB=15,sinA= ,
求AC和BC.9.在等腰△ABC中,AB=AC=13,BC=10,
求sinB,cosB.随堂练习110. 如图,分别求∠α,∠β的正弦,余弦,和正切.11.在△ABC中,AB=5,BC=13,AD是BC边上的高,AD=4.求:CD,sinC.12.在Rt△ABC中,∠BCA=90°,CD是中线,BC=8,CD=5.
求sin∠ACD,cos∠ACD和tan∠ACD.13.在Rt△ABC中,∠C=90°,sinA和cosB有什么关系?随堂练习14. 在Rt△ABC中,∠C=90°.
(1)AC=25.AB=27.求sinA,cosA,tanA, 和sinB,cosB,tanB,.
(2)BC=3,sinA=0.6,求AC 和AB.
(3)AC=4,cosA=0.8,求BC.15.在梯形ABCD中,AD//BC,AB=DC=13,AD=8,BC=18.
求:sinB,cosB,tanB.驶向胜利的彼岸随堂练习
