2.5二次函数与一元二次方程课件(第1课时)
文档属性
| 名称 | 2.5二次函数与一元二次方程课件(第1课时) |  | |
| 格式 | zip | ||
| 文件大小 | 636.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-01-06 23:53:34 | ||
图片预览



文档简介
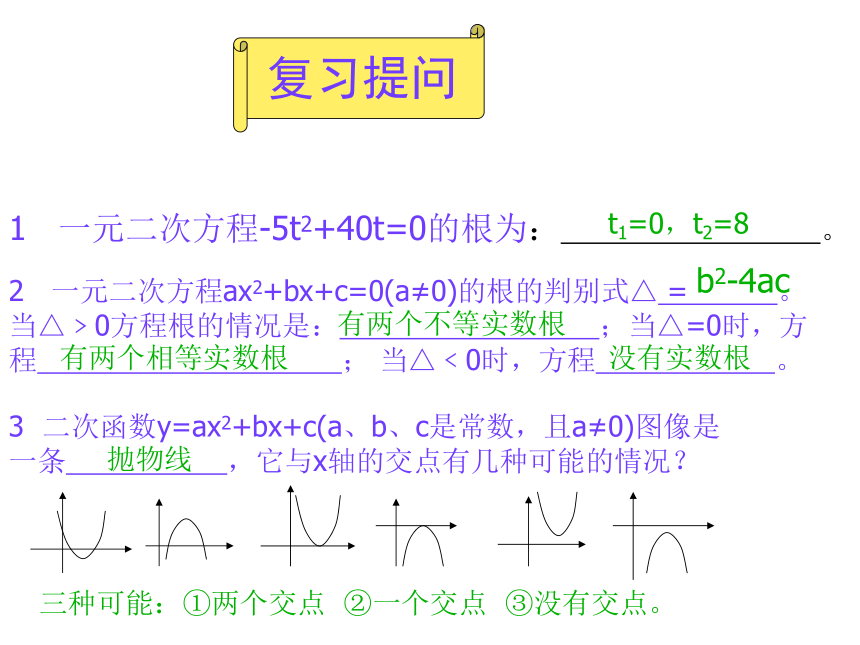
课件9张PPT。2.5二次函数与一元二次方程(第1课时)北师大版九年级下册第二章《二次函数》1 一元二次方程-5t2+40t=0的根为: 。2 一元二次方程ax2+bx+c=0(a≠0)的根的判别式△ = 。
当△﹥0方程根的情况是: ;当△=0时,方
程 ; 当△﹤0时,方程 。b2-4ac有两个不等实数根有两个相等实数根没有实数根t1=0,t2=83 二次函数y=ax2+bx+c(a、b、c是常数,且a≠0)图像是一条 ,它与x轴的交点有几种可能的情况?抛物线三种可能:①两个交点 ②一个交点 ③没有交点。复习提问(1).h和t的关系式是什么?
(2).小球经过多少秒后落地?你有几种求解方法?与同伴进行交流.我们已经知道,竖直上抛物体的高度h(m)与运动时间t(s)的关系可用公式h=-5t2+v0t+h0表示,其中h0(m)是抛出时的高度,v0(m/s)是抛出时的速度.一个小球从地面以40m/s的速度竖直向上抛出起,小球的高度h(m)与运动时间t(s)的关系如图所示,那么活动探究10t2468h20406080100活动探究23 抛物线y=x2-4x+4与轴有 个交点,坐标是 。1 若方程ax2+bx+c=0的根为x1=-2和x2=3,则二次函数
y=ax2+bx+c的图象与x轴交点坐标是 。2 抛物线y=0.5x2-x+3与x轴的交点情况是( )
A 两个交点 B 一个交点 C 没有交点 D 画出图象后才能说明(-2,0)和(3,0)c1(2,0)课堂练习4 不画图象,求抛物线y=x2-3x-4与x轴的交点坐标。解:∵解方程x2-3x-4=0得:
x1=-1,x2=4
∴抛物线y=x2-3x-4与x轴的交点坐标是:
(-1,0)和(4,0)101xyMN232y=x2-4x+4 5 一元二次方程x2-4x+4=1的根与二次函数y=x2-4x+4的图象有什么关系?试把方程的根在图象上表示出来。课堂练习二次函数y=ax2+bx+c何时为一元二次方程?它们的关系如何?在本节一开始的小球上抛问题中,何时小球离地面的高度是60m?你是如何知道的?知识升华∴抛出去后第2秒和第6秒时,离地面60米课堂寄语 二次函数与一元二次方程的关系,体现了“数形结合”这一重要的数学思想方法。也启示我们只要善于观察和思考,就能发现事物之间的各种联系,去探索科学的奥秘。再见
当△﹥0方程根的情况是: ;当△=0时,方
程 ; 当△﹤0时,方程 。b2-4ac有两个不等实数根有两个相等实数根没有实数根t1=0,t2=83 二次函数y=ax2+bx+c(a、b、c是常数,且a≠0)图像是一条 ,它与x轴的交点有几种可能的情况?抛物线三种可能:①两个交点 ②一个交点 ③没有交点。复习提问(1).h和t的关系式是什么?
(2).小球经过多少秒后落地?你有几种求解方法?与同伴进行交流.我们已经知道,竖直上抛物体的高度h(m)与运动时间t(s)的关系可用公式h=-5t2+v0t+h0表示,其中h0(m)是抛出时的高度,v0(m/s)是抛出时的速度.一个小球从地面以40m/s的速度竖直向上抛出起,小球的高度h(m)与运动时间t(s)的关系如图所示,那么活动探究10t2468h20406080100活动探究23 抛物线y=x2-4x+4与轴有 个交点,坐标是 。1 若方程ax2+bx+c=0的根为x1=-2和x2=3,则二次函数
y=ax2+bx+c的图象与x轴交点坐标是 。2 抛物线y=0.5x2-x+3与x轴的交点情况是( )
A 两个交点 B 一个交点 C 没有交点 D 画出图象后才能说明(-2,0)和(3,0)c1(2,0)课堂练习4 不画图象,求抛物线y=x2-3x-4与x轴的交点坐标。解:∵解方程x2-3x-4=0得:
x1=-1,x2=4
∴抛物线y=x2-3x-4与x轴的交点坐标是:
(-1,0)和(4,0)101xyMN232y=x2-4x+4 5 一元二次方程x2-4x+4=1的根与二次函数y=x2-4x+4的图象有什么关系?试把方程的根在图象上表示出来。课堂练习二次函数y=ax2+bx+c何时为一元二次方程?它们的关系如何?在本节一开始的小球上抛问题中,何时小球离地面的高度是60m?你是如何知道的?知识升华∴抛出去后第2秒和第6秒时,离地面60米课堂寄语 二次函数与一元二次方程的关系,体现了“数形结合”这一重要的数学思想方法。也启示我们只要善于观察和思考,就能发现事物之间的各种联系,去探索科学的奥秘。再见
