第14章勾股定理单元测试题(含解析)
文档属性
| 名称 | 第14章勾股定理单元测试题(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 97.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-01-07 09:22:20 | ||
图片预览


文档简介
八年级数学单元试题《勾股定理》
一、选择题:(每小题3分,共30分)
1、在中,∠A、∠B、∠C的对边分别是a、b、c,下列条件中,能判断为直角三角形的是( )
A、a+b=c B、a:b:c=3:4:5 C、a=b=2 D、∠A=∠B=∠C
2、若三角形三边长分别是6,8,10,则它最长边上的高为( )
A、 6 B、4.8 C、 2.4 D、821世纪教育网版权所有
3、如图所示,直角三边形三边上的半圆面积从小到大依次记为S1、S2、S3,则S1、S2、S3的关系是( )21教育网
A、S1+S2=S3 B、S12+S22=S32 C、S1+S2>S3 D、 S1+S24、如图,正方形网格中的,若小方格边长为1,则是( )
A、直角三角形 B、锐角三角形 C、钝角三角形 D、以上答案都不对
5、如图,小方格都是面积为1的矩形,则图中四边形的面积是 ( )
A、 25 B、 12.5 C、 9 D、 8.5
6、在中,BC=3,AC=4,AB=5,把沿最长边AB翻折成ABD,则CD的长为 ( ) A、 B、 C、 D、2·1·c·n·j·y
7、在Rt中,∠C=90,周长为60,斜边与一条直角边之比为13∶5,则这个三角形三边长分别是 ( )【来源:21·世纪·教育·网】
A、5,4,3 B、13,12,5 C、10,8,6 D、26,24,10
8、如图,一圆柱高8cm,底面半径2cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程( 取3)是( )21·世纪*教育网
A、20cm B、10cm C、14cm D、无法确定
9、若等边的边长为2cm,那么的面积为( )
A、cm2 B、cm2 C、cm2 D、4cm2
10、若等腰三角形中相等的两边长为10cm,第三边长为16 cm,那么第三边上的高为 ( )
A、 12 cm B、 10 cm C、 8 cm D、 6 cm21*cnjy*com
二、填空题:(每小题3分,共30分)
11、 已知甲往东走了4km,乙往南走了3km,这时甲、乙两人相距
12、在Rt中,斜边AB=2,则AB2+BC2+CA2= .
13、已知|x-12|+|x+y-25|与z2-10z+25互为相反数,则以x、y、z为三边的三角形是 三角形. 【来源:21cnj*y.co*m】
14、 如图,有一块直角三角形纸片,两直角边AC=6cm,BC=8cm,先将直角边AC沿AD折叠,使它落在斜边AB上,且与AE重合,则CD= 【版权所有:21教育】
15、等腰的底边BC为16,底边上的高AD为6,则腰长AB为
16、若正方形的面积为18cm2,则正方形对角线长为 cm。
17、一个直角三角形的两边长分别为3cm和4cm,则第三边的长为
18、在中,AB=12cm, BC=16cm, AC=20cm, 则的面积是
19、如图,利用三个正方形可以拼成一个三角形,如果有三个面积从小到大依次为,,的正方形,能拼围成一个直角三角形,则,之间的关系是 21教育名师原创作品
20、在中,AB=13,AC=15,BC边上的高AD=12,则BC的长为
三、(每小题7分,共28分)
21、如图,在ΔABC中,∠ACB=900,AB=5cm,BC=3cm,CD⊥AB于D。
求:(1)AC的长; (2)ΔABC的面积; (3)CD的长。
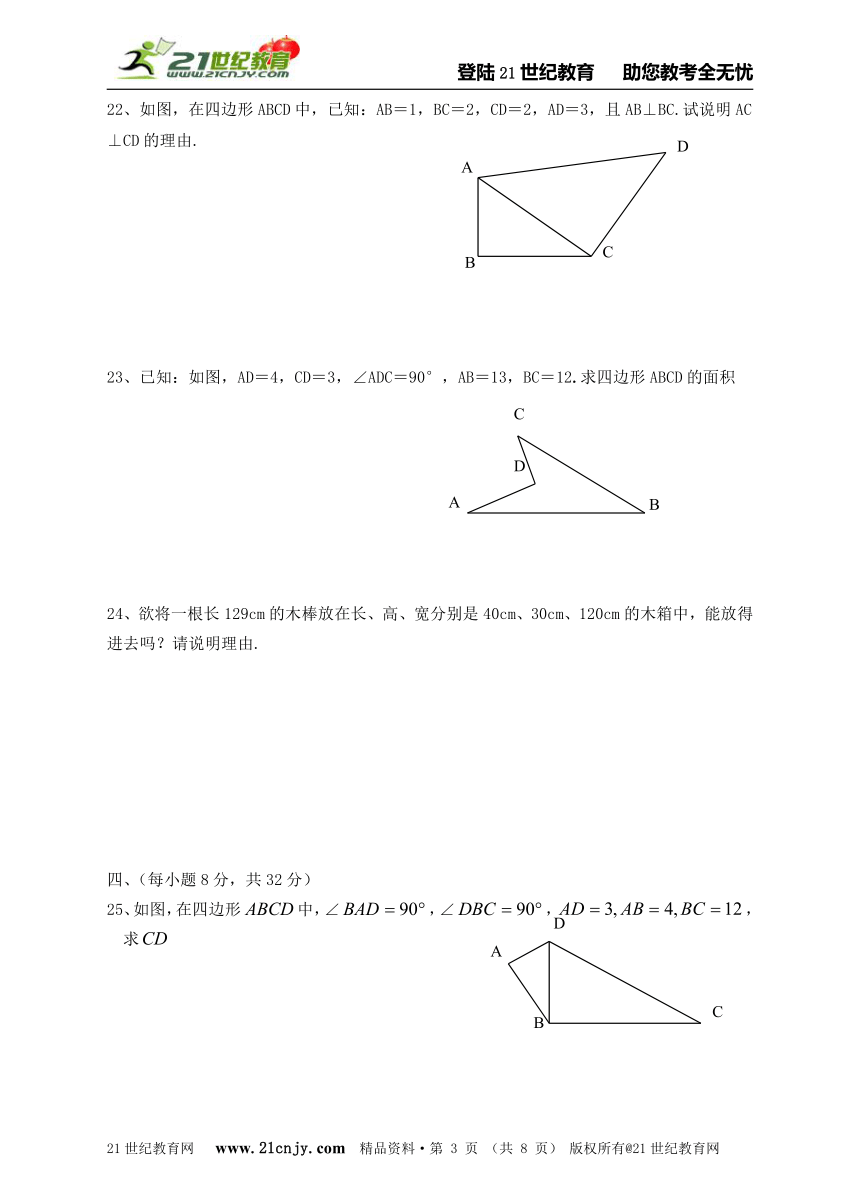
22、如图,在四边形ABCD中,已知:AB=1,BC=2,CD=2,AD=3,且AB⊥BC.试说明AC⊥CD的理由.www-2-1-cnjy-com
23、已知:如图,AD=4,CD=3,∠ADC=90°,AB=13,BC=12.求四边形ABCD的面积
24、欲将一根长129cm的木棒放在长、高、宽分别是40cm、30cm、120cm的木箱中,能放得进去吗?请说明理由.【出处:21教育名师】
四、(每小题8分,共32分)
25、如图,在四边形中,∠,∠,,求
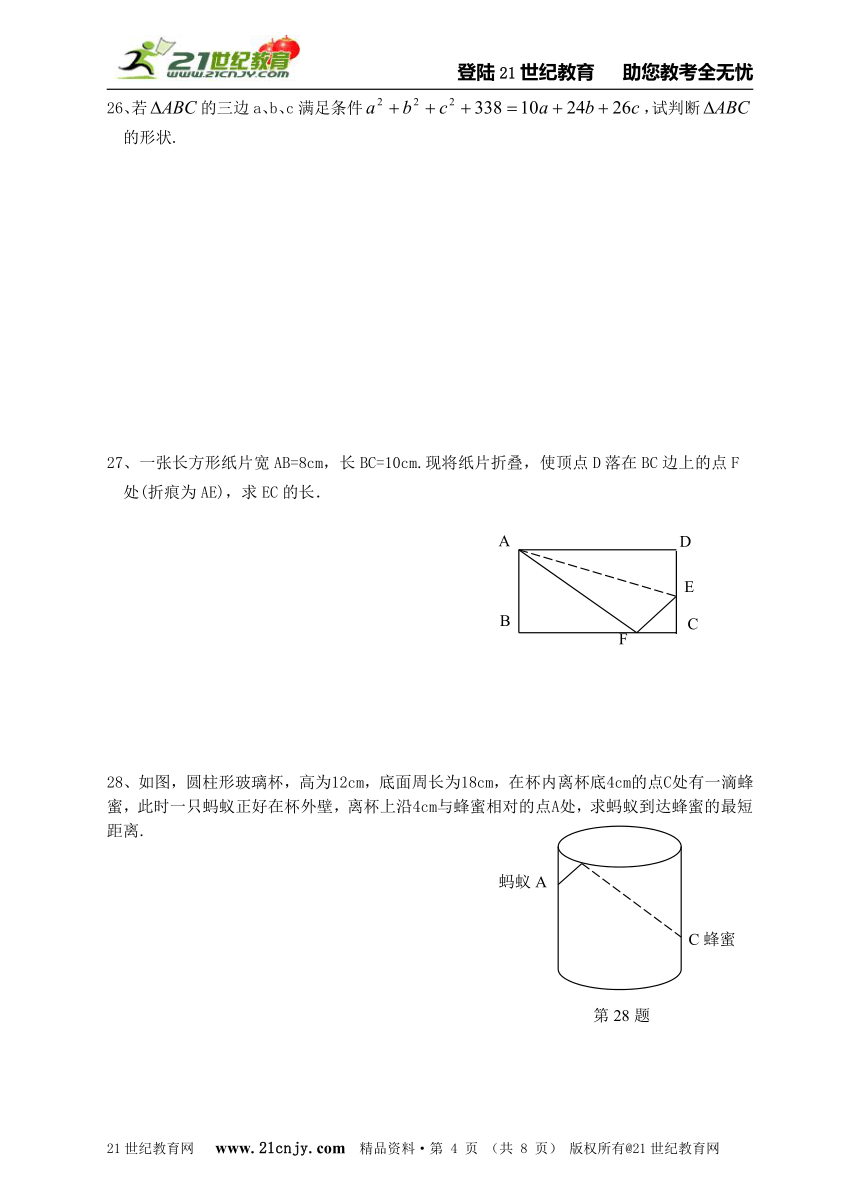
26、若的三边a、b、c满足条件,试判断的形状.
27、一张长方形纸片宽AB=8cm,长BC=10cm.现将纸片折叠,使顶点D落在BC边上的点F处(折痕为AE),求EC的长.2-1-c-n-j-y
28、如图,圆柱形玻璃杯,高为12cm,底面周长为18cm,在杯内离杯底4cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,求蚂蚁到达蜂蜜的最短距离.21·cn·jy·com
八年级数学单元试题《勾股定理》参考答案
一、选择题:
4、A 解析:∵,,
∴∴∠A=90°
5、B 解析:
6、C 解析:∵沿最长边AB翻折成ABD∴AC=AD,∠CAB=∠DAB∴AB⊥CD∵∴∠ACB=90°,利用面积关系建立方程:∴h=2.4∴CD=4.8
7、D 解析:设没份为x,,
∴5x+12x+13x=60∴x=2∴三边为26,24,10
8、B 解析:
9、A 解析:要求面积就作一边上的高,利用三线合一,勾股定理,三角形的面积公式底乘高的一半。
10、C 解析:作第三边上的高,利用三线合一,勾股定理。
二、填空题:
11、5km 解析:向东和向南正好是直角,根据勾股定理可求出。
12、8 解析:∵在Rt中,斜边AB=2∴
∴
13、直角
解析:∵|x-12|+|x+y-25|与z2-10z+25互为相反数
∴|x-12|+|x+y-25|+z2-10z+25=0
∴|x-12|+|x+y-25|+ =0
∵,,
∴,,
∴,,
∴
∴
∴
∴此三角形是直角三角形
14、3cm
解析:∵两直角边AC=6cm,BC=8cm
∴,设CD=x,则BD=8-x,BE=10-6=4∴∴x=3
15、10 解析:利用三线合一,勾股定理即可
16、6 解析:设正方形的边长为xcm,则∴对角线长为
17、5cm或cm 解析:分两种情况:直角边为3cm和4cm,求斜边;斜边为4cm和一直角边为3cm,求另一直角边21cnjy.com
18、
解析:∵
∴∴∠B=90°∴
19、 解析:正方形的面积正好是边长的平方,再根据勾股定理
20、14或4 解析:此题没有图形,有两种图形所以有两种答案。
∵BC边上的高AD=12∴
∴
三、
21、解:(1)在RtΔABC中
(2)
(3)∵CD⊥AB∴∴CD=
22、解:∵∴∵CD=2
∴∵AD=3∴∴
∴AC⊥CD
23、解:连结AC
∵∠ADC=90°,AD=4,CD=3
∴
∵AB=13,BC=12∴
∴
∴∠ACB=90°
∴
=
24、解:连结BE,EC
在Rt中,
在Rt中,
∴130>129∴能将一根长129cm的木棒放在木箱中
四、
25、解:在Rt中,
在Rt中,
26、解:∵
∴
∴
∴
∵
∴
∴
∴
∴
∴
∴△ABC是直角三角形
27、解:∵顶点D落在BC边上的点F处
∴AD=AF,DE=FE
∵长方形ABCD
∴AD=BC=10cm,AB=CD=8cm
∴AF=10cm,
在Rt中,
∴
设CE=x,则DE=EF=8-x
在Rt中,
解这个方程得x=3cm
28、解析:点A关于杯口所在直线的对称点B,连结BC,BC就是最短的距离。
BD就是底面周长的一半,BD=9cm
因点C离杯底的距离为4cm,点A离杯口的距离为4cm,杯高12cm,所以CD=12cm
在Rt中,cm
一、选择题:(每小题3分,共30分)
1、在中,∠A、∠B、∠C的对边分别是a、b、c,下列条件中,能判断为直角三角形的是( )
A、a+b=c B、a:b:c=3:4:5 C、a=b=2 D、∠A=∠B=∠C
2、若三角形三边长分别是6,8,10,则它最长边上的高为( )
A、 6 B、4.8 C、 2.4 D、821世纪教育网版权所有
3、如图所示,直角三边形三边上的半圆面积从小到大依次记为S1、S2、S3,则S1、S2、S3的关系是( )21教育网
A、S1+S2=S3 B、S12+S22=S32 C、S1+S2>S3 D、 S1+S2
A、直角三角形 B、锐角三角形 C、钝角三角形 D、以上答案都不对
5、如图,小方格都是面积为1的矩形,则图中四边形的面积是 ( )
A、 25 B、 12.5 C、 9 D、 8.5
6、在中,BC=3,AC=4,AB=5,把沿最长边AB翻折成ABD,则CD的长为 ( ) A、 B、 C、 D、2·1·c·n·j·y
7、在Rt中,∠C=90,周长为60,斜边与一条直角边之比为13∶5,则这个三角形三边长分别是 ( )【来源:21·世纪·教育·网】
A、5,4,3 B、13,12,5 C、10,8,6 D、26,24,10
8、如图,一圆柱高8cm,底面半径2cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程( 取3)是( )21·世纪*教育网
A、20cm B、10cm C、14cm D、无法确定
9、若等边的边长为2cm,那么的面积为( )
A、cm2 B、cm2 C、cm2 D、4cm2
10、若等腰三角形中相等的两边长为10cm,第三边长为16 cm,那么第三边上的高为 ( )
A、 12 cm B、 10 cm C、 8 cm D、 6 cm21*cnjy*com
二、填空题:(每小题3分,共30分)
11、 已知甲往东走了4km,乙往南走了3km,这时甲、乙两人相距
12、在Rt中,斜边AB=2,则AB2+BC2+CA2= .
13、已知|x-12|+|x+y-25|与z2-10z+25互为相反数,则以x、y、z为三边的三角形是 三角形. 【来源:21cnj*y.co*m】
14、 如图,有一块直角三角形纸片,两直角边AC=6cm,BC=8cm,先将直角边AC沿AD折叠,使它落在斜边AB上,且与AE重合,则CD= 【版权所有:21教育】
15、等腰的底边BC为16,底边上的高AD为6,则腰长AB为
16、若正方形的面积为18cm2,则正方形对角线长为 cm。
17、一个直角三角形的两边长分别为3cm和4cm,则第三边的长为
18、在中,AB=12cm, BC=16cm, AC=20cm, 则的面积是
19、如图,利用三个正方形可以拼成一个三角形,如果有三个面积从小到大依次为,,的正方形,能拼围成一个直角三角形,则,之间的关系是 21教育名师原创作品
20、在中,AB=13,AC=15,BC边上的高AD=12,则BC的长为
三、(每小题7分,共28分)
21、如图,在ΔABC中,∠ACB=900,AB=5cm,BC=3cm,CD⊥AB于D。
求:(1)AC的长; (2)ΔABC的面积; (3)CD的长。
22、如图,在四边形ABCD中,已知:AB=1,BC=2,CD=2,AD=3,且AB⊥BC.试说明AC⊥CD的理由.www-2-1-cnjy-com
23、已知:如图,AD=4,CD=3,∠ADC=90°,AB=13,BC=12.求四边形ABCD的面积
24、欲将一根长129cm的木棒放在长、高、宽分别是40cm、30cm、120cm的木箱中,能放得进去吗?请说明理由.【出处:21教育名师】
四、(每小题8分,共32分)
25、如图,在四边形中,∠,∠,,求
26、若的三边a、b、c满足条件,试判断的形状.
27、一张长方形纸片宽AB=8cm,长BC=10cm.现将纸片折叠,使顶点D落在BC边上的点F处(折痕为AE),求EC的长.2-1-c-n-j-y
28、如图,圆柱形玻璃杯,高为12cm,底面周长为18cm,在杯内离杯底4cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,求蚂蚁到达蜂蜜的最短距离.21·cn·jy·com
八年级数学单元试题《勾股定理》参考答案
一、选择题:
4、A 解析:∵,,
∴∴∠A=90°
5、B 解析:
6、C 解析:∵沿最长边AB翻折成ABD∴AC=AD,∠CAB=∠DAB∴AB⊥CD∵∴∠ACB=90°,利用面积关系建立方程:∴h=2.4∴CD=4.8
7、D 解析:设没份为x,,
∴5x+12x+13x=60∴x=2∴三边为26,24,10
8、B 解析:
9、A 解析:要求面积就作一边上的高,利用三线合一,勾股定理,三角形的面积公式底乘高的一半。
10、C 解析:作第三边上的高,利用三线合一,勾股定理。
二、填空题:
11、5km 解析:向东和向南正好是直角,根据勾股定理可求出。
12、8 解析:∵在Rt中,斜边AB=2∴
∴
13、直角
解析:∵|x-12|+|x+y-25|与z2-10z+25互为相反数
∴|x-12|+|x+y-25|+z2-10z+25=0
∴|x-12|+|x+y-25|+ =0
∵,,
∴,,
∴,,
∴
∴
∴
∴此三角形是直角三角形
14、3cm
解析:∵两直角边AC=6cm,BC=8cm
∴,设CD=x,则BD=8-x,BE=10-6=4∴∴x=3
15、10 解析:利用三线合一,勾股定理即可
16、6 解析:设正方形的边长为xcm,则∴对角线长为
17、5cm或cm 解析:分两种情况:直角边为3cm和4cm,求斜边;斜边为4cm和一直角边为3cm,求另一直角边21cnjy.com
18、
解析:∵
∴∴∠B=90°∴
19、 解析:正方形的面积正好是边长的平方,再根据勾股定理
20、14或4 解析:此题没有图形,有两种图形所以有两种答案。
∵BC边上的高AD=12∴
∴
三、
21、解:(1)在RtΔABC中
(2)
(3)∵CD⊥AB∴∴CD=
22、解:∵∴∵CD=2
∴∵AD=3∴∴
∴AC⊥CD
23、解:连结AC
∵∠ADC=90°,AD=4,CD=3
∴
∵AB=13,BC=12∴
∴
∴∠ACB=90°
∴
=
24、解:连结BE,EC
在Rt中,
在Rt中,
∴130>129∴能将一根长129cm的木棒放在木箱中
四、
25、解:在Rt中,
在Rt中,
26、解:∵
∴
∴
∴
∵
∴
∴
∴
∴
∴
∴△ABC是直角三角形
27、解:∵顶点D落在BC边上的点F处
∴AD=AF,DE=FE
∵长方形ABCD
∴AD=BC=10cm,AB=CD=8cm
∴AF=10cm,
在Rt中,
∴
设CE=x,则DE=EF=8-x
在Rt中,
解这个方程得x=3cm
28、解析:点A关于杯口所在直线的对称点B,连结BC,BC就是最短的距离。
BD就是底面周长的一半,BD=9cm
因点C离杯底的距离为4cm,点A离杯口的距离为4cm,杯高12cm,所以CD=12cm
在Rt中,cm
