第3、4章 投影与视图和概率 综合测试(含答案)
文档属性
| 名称 | 第3、4章 投影与视图和概率 综合测试(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-01-09 00:00:00 | ||
图片预览


文档简介
第3、4章
投影与视图和概率
综合测试
一.选择题(共8小题)
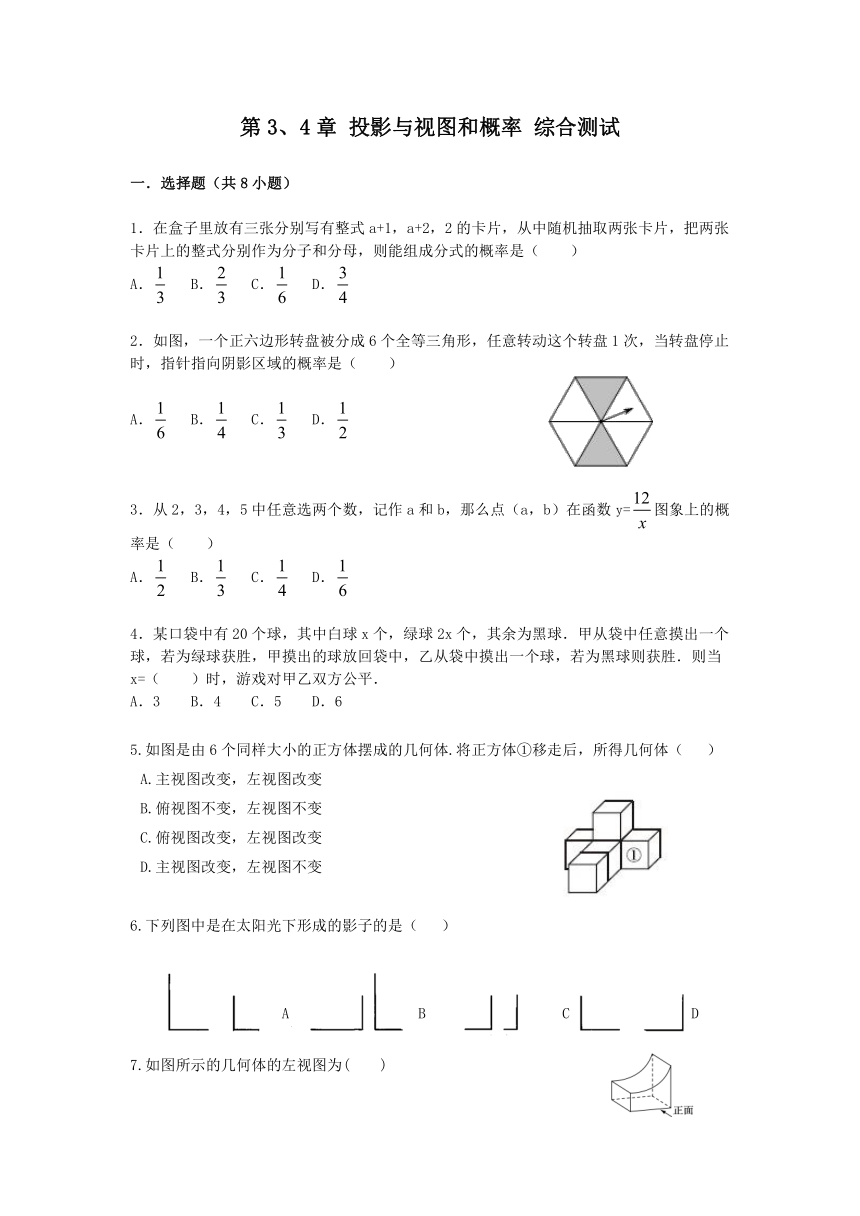
1.在盒子里放有三张分别写有整式a+1,a+2,2的卡片,从中随机抽取两张卡片,把两张卡片上的整式分别作为分子和分母,则能组成分式的概率是( )
A.
B.
C.
D.
2.如图,一个正六边形转盘被分成6个全等三角形,任意转动这个转盘1次,当转盘停止时,指针指向阴影区域的概率是( )
A.
B.
C.
D.
3.从2,3,4,5中任意选两个数,记作a和b,那么点(a,b)在函数y=图象上的概率是( )
A.
B.
C.
D.
4.某口袋中有20个球,其中白球x个,绿球2x个,其余为黑球.甲从袋中任意摸出一个球,若为绿球获胜,甲摸出的球放回袋中,乙从袋中摸出一个球,若为黑球则获胜.则当x=( )时,游戏对甲乙双方公平.
A.3
B.4
C.5
D.6
5.如图是由6个同样大小的正方体摆成的几何体.将正方体①移走后,所得几何体(
)
A.主视图改变,左视图改变
B.俯视图不变,左视图不变
C.俯视图改变,左视图改变
D.主视图改变,左视图不变
6.下列图中是在太阳光下形成的影子的是(
)
A
B
C
D
7.如图所示的几何体的左视图为( )
A.
B.
C.
D.
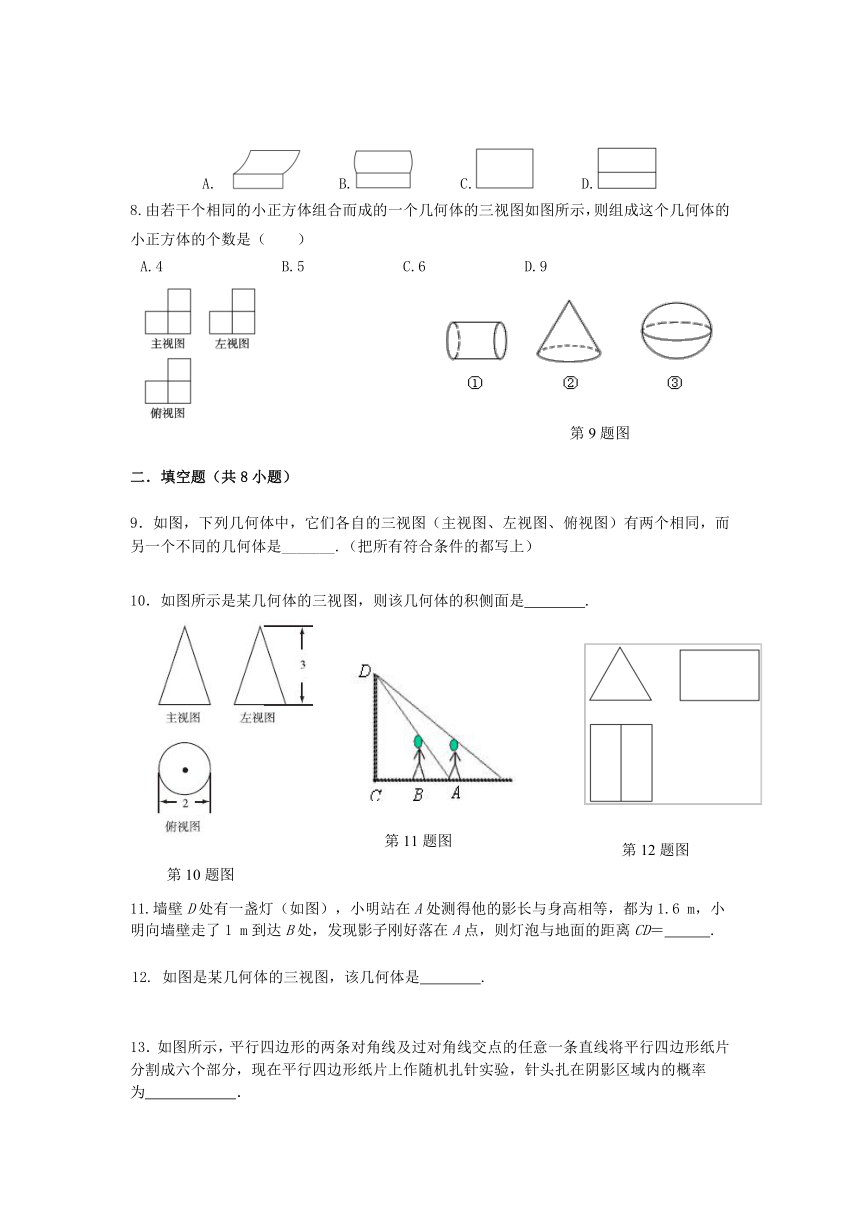
8.由若干个相同的小正方体组合而成的一个几何体的三视图如图所示,则组成这个几何体的小正方体的个数是( )
A.4
B.5
C.6
D.9
二.填空题(共8小题)
9.如图,下列几何体中,它们各自的三视图(主视图、左视图、俯视图)有两个相同,而另一个不同的几何体是_______.(把所有符合条件的都写上)
10.如图所示是某几何体的三视图,则该几何体的积侧面是
.
11.墙壁D处有一盏灯(如图),小明站在A处测得他的影长与身高相等,都为1.6
m,小明向墙壁走了1
m到达B处,发现影子刚好落在A点,则灯泡与地面的距离CD=
.
12.
如图是某几何体的三视图,该几何体是
.
13.如图所示,平行四边形的两条对角线及过对角线交点的任意一条直线将平行四边形纸片分割成六个部分,现在平行四边形纸片上作随机扎针实验,针头扎在阴影区域内的概率为 .
14.小明和小红用摸球游戏决定谁去看电影,袋中有2个红球和1个白球(除颜色外都相同),摸到红球小明去看,摸到白球小红去看,游戏对双方是
(填“公平”或不公平)的.
15.在一个不透明的袋中装有除颜色外其余均相同的n个小球,其中有5个黑球,从袋中随机摸出一球,记下其颜色,这称为一次摸球试验,之后把它放回袋中,搅匀后,再继续摸出一球,以下是利用计算机模拟的摸球试验次数与摸出黑球次数的列表:
摸球试验次数
100
1000
5000
10000
50000
100000
摸出黑球次数
46
487
2506
5008
24996
50007
根据列表,可以估计出n的值是 .
16.用2,3,4三个数字排成一个三位数,则排出的数是偶数的概率为 .
三.解答题(共7小题)
17.下列8个事件中:
(1)掷一枚硬币,正面朝上.
(2)打开电视机,正在播电视剧.
(3)随意翻开一本有400页的书,正好翻到第200页.
(4)天上下雨,马路潮湿.
(5)你能长到身高5米.
(6)买奖券中特等大奖.
(7)掷一枚骰子的得到的点数小于8.
(8)2005年6月27日是星期一.
其中(将序号填入题中的横线上即可)
不可能事件为 ;必然事件为 ;不确定事件中,发生可能性最大的是 ,发生可能性最小的是 .
18.如图,某同学想测量旗杆的高度,他在某一时刻测得1
m长的竹竿竖直放置时影长1.5
m,在同一时刻测量旗杆的影长时,因旗杆靠近一楼房,影子不全落在地面上,有一部分落在墙上,他测得落在地面上的影长为21
m,留在墙上的影高为2
m,求旗杆的高度.
19.一个不透明的口袋中装有2个红球(记为红球1、红球2),1个白球、1个黑球,这些球除颜色外都相同,将球搅匀.
(1)从中任意摸出1个球,恰好摸到红球的概率是
(2)先从中任意摸出一个球,再从余下的3个球中任意摸出1个球,请用列举法(画树状图或列表),求两次都摸到红球的概率.
20.如图,小赵和路人在路灯下行走,试确定图中路灯灯泡的位置,并画出小赵在灯光下的影子.
21.
802班组织学生参加汉字听写比赛,比赛分为甲乙丙三组进行,下面两幅统计图反映了学生参加比赛的报名情况,请你根据图中信息回答下列问题:
(1)该班报名参加本次活动的总人数为 人.
(2)该班报名参加丙组的人数为 人,并补全频数分布直方图;
(3)比赛后选取男女各2名同学进行培训,若从中选2名参加校赛,试用列表或画树状图的方法,求恰好选中一男一女的概率.
22.(8分)如图所示为一机器零件的三视图.
(1)请写出符合这个机器零件形状的几何体的名称.
(2)若俯视图中三角形为正三角形,那么请根据图中所标的尺寸,计算这个几何体的表面积(单位:cm2).
23.某商场为了吸引顾客,设计了一个摸球获奖的箱子,箱子中共有20个球,其中红球2个,兰球3个,黄球5个,白球10个,并规定购买100元的商品,就有一次摸球的机会,摸到红、兰、黄、白球的(一次只能摸一个),顾客就可以分别得到80元、30元、10元、0元购物卷,凭购物卷仍然可以在商场购买,如果顾客不愿意摸球,那么可以直接获得购物卷10元.
(1)每摸一次球所获购物卷金额的平均值是多少?
(2)你若在此商场购买100元的货物,两种方式中你应选择哪种方式?为什么?
参考答案:
一.选择题(共8小题)
1.B
2.C
3.D
4.B
5.D
6.A
7.D
8.A
一.填空题(共8小题)
9.
①②
10.
11.
12.正三棱柱
13.
14.不公平
15.
16.
三.解答题(共7小题)
17.不可能事件为 (5) ;必然事件为 (4)(7)(8) ;不确定事件中,发生可能性最大的是 (1) ,发生可能性最小的是 (6) .
18.
.
19.解:(1)4个小球中有2个红球,则任意摸出1个球,恰好摸到红球的概率是;
故答案为:;
(2)列表如下:
红
红
白
黑
红
﹣﹣﹣
(红,红)
(白,红)
(黑,红)
红
(红,红)
﹣﹣﹣
(白,红)
(黑,红)
白
(红,白)
(红,白)
﹣﹣﹣
(黑,白)
黑
(红,黑)
(红,黑)
(白,黑)
﹣﹣﹣
所有等可能的情况有12种,其中两次都摸到红球有2种可能,
则P(两次摸到红球)==.
20略
21.
解:(1)15÷30%=50人,
(2)50×50%=25人,
(3)设男生为A,B;女生为a,b.
列树状图:
P(男女)==.
故答案为50,25.
22.
解:(1)符合这个零件的几何体是直三棱柱.
(2)如图,△是正三角形,⊥,2,,
在Rt△ADC中,,
解得AC=4.
(cm2).
23.
解:(1)∵P(摸到红球)=,P(摸到兰球)=,P(摸到黄球)=,P(摸到白球)=,
∴每摸一次球所获购物卷金额的平均值为:80×+30×+10×=15(元);
(2)∵15>10,
∴两种方式中我会选择摸球这种方式,此时较合算.
第9题图
第12题图
第11题图
第10题图
第13题图
投影与视图和概率
综合测试
一.选择题(共8小题)
1.在盒子里放有三张分别写有整式a+1,a+2,2的卡片,从中随机抽取两张卡片,把两张卡片上的整式分别作为分子和分母,则能组成分式的概率是( )
A.
B.
C.
D.
2.如图,一个正六边形转盘被分成6个全等三角形,任意转动这个转盘1次,当转盘停止时,指针指向阴影区域的概率是( )
A.
B.
C.
D.
3.从2,3,4,5中任意选两个数,记作a和b,那么点(a,b)在函数y=图象上的概率是( )
A.
B.
C.
D.
4.某口袋中有20个球,其中白球x个,绿球2x个,其余为黑球.甲从袋中任意摸出一个球,若为绿球获胜,甲摸出的球放回袋中,乙从袋中摸出一个球,若为黑球则获胜.则当x=( )时,游戏对甲乙双方公平.
A.3
B.4
C.5
D.6
5.如图是由6个同样大小的正方体摆成的几何体.将正方体①移走后,所得几何体(
)
A.主视图改变,左视图改变
B.俯视图不变,左视图不变
C.俯视图改变,左视图改变
D.主视图改变,左视图不变
6.下列图中是在太阳光下形成的影子的是(
)
A
B
C
D
7.如图所示的几何体的左视图为( )
A.
B.
C.
D.
8.由若干个相同的小正方体组合而成的一个几何体的三视图如图所示,则组成这个几何体的小正方体的个数是( )
A.4
B.5
C.6
D.9
二.填空题(共8小题)
9.如图,下列几何体中,它们各自的三视图(主视图、左视图、俯视图)有两个相同,而另一个不同的几何体是_______.(把所有符合条件的都写上)
10.如图所示是某几何体的三视图,则该几何体的积侧面是
.
11.墙壁D处有一盏灯(如图),小明站在A处测得他的影长与身高相等,都为1.6
m,小明向墙壁走了1
m到达B处,发现影子刚好落在A点,则灯泡与地面的距离CD=
.
12.
如图是某几何体的三视图,该几何体是
.
13.如图所示,平行四边形的两条对角线及过对角线交点的任意一条直线将平行四边形纸片分割成六个部分,现在平行四边形纸片上作随机扎针实验,针头扎在阴影区域内的概率为 .
14.小明和小红用摸球游戏决定谁去看电影,袋中有2个红球和1个白球(除颜色外都相同),摸到红球小明去看,摸到白球小红去看,游戏对双方是
(填“公平”或不公平)的.
15.在一个不透明的袋中装有除颜色外其余均相同的n个小球,其中有5个黑球,从袋中随机摸出一球,记下其颜色,这称为一次摸球试验,之后把它放回袋中,搅匀后,再继续摸出一球,以下是利用计算机模拟的摸球试验次数与摸出黑球次数的列表:
摸球试验次数
100
1000
5000
10000
50000
100000
摸出黑球次数
46
487
2506
5008
24996
50007
根据列表,可以估计出n的值是 .
16.用2,3,4三个数字排成一个三位数,则排出的数是偶数的概率为 .
三.解答题(共7小题)
17.下列8个事件中:
(1)掷一枚硬币,正面朝上.
(2)打开电视机,正在播电视剧.
(3)随意翻开一本有400页的书,正好翻到第200页.
(4)天上下雨,马路潮湿.
(5)你能长到身高5米.
(6)买奖券中特等大奖.
(7)掷一枚骰子的得到的点数小于8.
(8)2005年6月27日是星期一.
其中(将序号填入题中的横线上即可)
不可能事件为 ;必然事件为 ;不确定事件中,发生可能性最大的是 ,发生可能性最小的是 .
18.如图,某同学想测量旗杆的高度,他在某一时刻测得1
m长的竹竿竖直放置时影长1.5
m,在同一时刻测量旗杆的影长时,因旗杆靠近一楼房,影子不全落在地面上,有一部分落在墙上,他测得落在地面上的影长为21
m,留在墙上的影高为2
m,求旗杆的高度.
19.一个不透明的口袋中装有2个红球(记为红球1、红球2),1个白球、1个黑球,这些球除颜色外都相同,将球搅匀.
(1)从中任意摸出1个球,恰好摸到红球的概率是
(2)先从中任意摸出一个球,再从余下的3个球中任意摸出1个球,请用列举法(画树状图或列表),求两次都摸到红球的概率.
20.如图,小赵和路人在路灯下行走,试确定图中路灯灯泡的位置,并画出小赵在灯光下的影子.
21.
802班组织学生参加汉字听写比赛,比赛分为甲乙丙三组进行,下面两幅统计图反映了学生参加比赛的报名情况,请你根据图中信息回答下列问题:
(1)该班报名参加本次活动的总人数为 人.
(2)该班报名参加丙组的人数为 人,并补全频数分布直方图;
(3)比赛后选取男女各2名同学进行培训,若从中选2名参加校赛,试用列表或画树状图的方法,求恰好选中一男一女的概率.
22.(8分)如图所示为一机器零件的三视图.
(1)请写出符合这个机器零件形状的几何体的名称.
(2)若俯视图中三角形为正三角形,那么请根据图中所标的尺寸,计算这个几何体的表面积(单位:cm2).
23.某商场为了吸引顾客,设计了一个摸球获奖的箱子,箱子中共有20个球,其中红球2个,兰球3个,黄球5个,白球10个,并规定购买100元的商品,就有一次摸球的机会,摸到红、兰、黄、白球的(一次只能摸一个),顾客就可以分别得到80元、30元、10元、0元购物卷,凭购物卷仍然可以在商场购买,如果顾客不愿意摸球,那么可以直接获得购物卷10元.
(1)每摸一次球所获购物卷金额的平均值是多少?
(2)你若在此商场购买100元的货物,两种方式中你应选择哪种方式?为什么?
参考答案:
一.选择题(共8小题)
1.B
2.C
3.D
4.B
5.D
6.A
7.D
8.A
一.填空题(共8小题)
9.
①②
10.
11.
12.正三棱柱
13.
14.不公平
15.
16.
三.解答题(共7小题)
17.不可能事件为 (5) ;必然事件为 (4)(7)(8) ;不确定事件中,发生可能性最大的是 (1) ,发生可能性最小的是 (6) .
18.
.
19.解:(1)4个小球中有2个红球,则任意摸出1个球,恰好摸到红球的概率是;
故答案为:;
(2)列表如下:
红
红
白
黑
红
﹣﹣﹣
(红,红)
(白,红)
(黑,红)
红
(红,红)
﹣﹣﹣
(白,红)
(黑,红)
白
(红,白)
(红,白)
﹣﹣﹣
(黑,白)
黑
(红,黑)
(红,黑)
(白,黑)
﹣﹣﹣
所有等可能的情况有12种,其中两次都摸到红球有2种可能,
则P(两次摸到红球)==.
20略
21.
解:(1)15÷30%=50人,
(2)50×50%=25人,
(3)设男生为A,B;女生为a,b.
列树状图:
P(男女)==.
故答案为50,25.
22.
解:(1)符合这个零件的几何体是直三棱柱.
(2)如图,△是正三角形,⊥,2,,
在Rt△ADC中,,
解得AC=4.
(cm2).
23.
解:(1)∵P(摸到红球)=,P(摸到兰球)=,P(摸到黄球)=,P(摸到白球)=,
∴每摸一次球所获购物卷金额的平均值为:80×+30×+10×=15(元);
(2)∵15>10,
∴两种方式中我会选择摸球这种方式,此时较合算.
第9题图
第12题图
第11题图
第10题图
第13题图
