第3章 投影与视图 同步测试(含答案)
文档属性
| 名称 | 第3章 投影与视图 同步测试(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 266.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-01-09 10:51:16 | ||
图片预览


文档简介
第3章
投影与视图
同步测试
一、选择题(8小题)
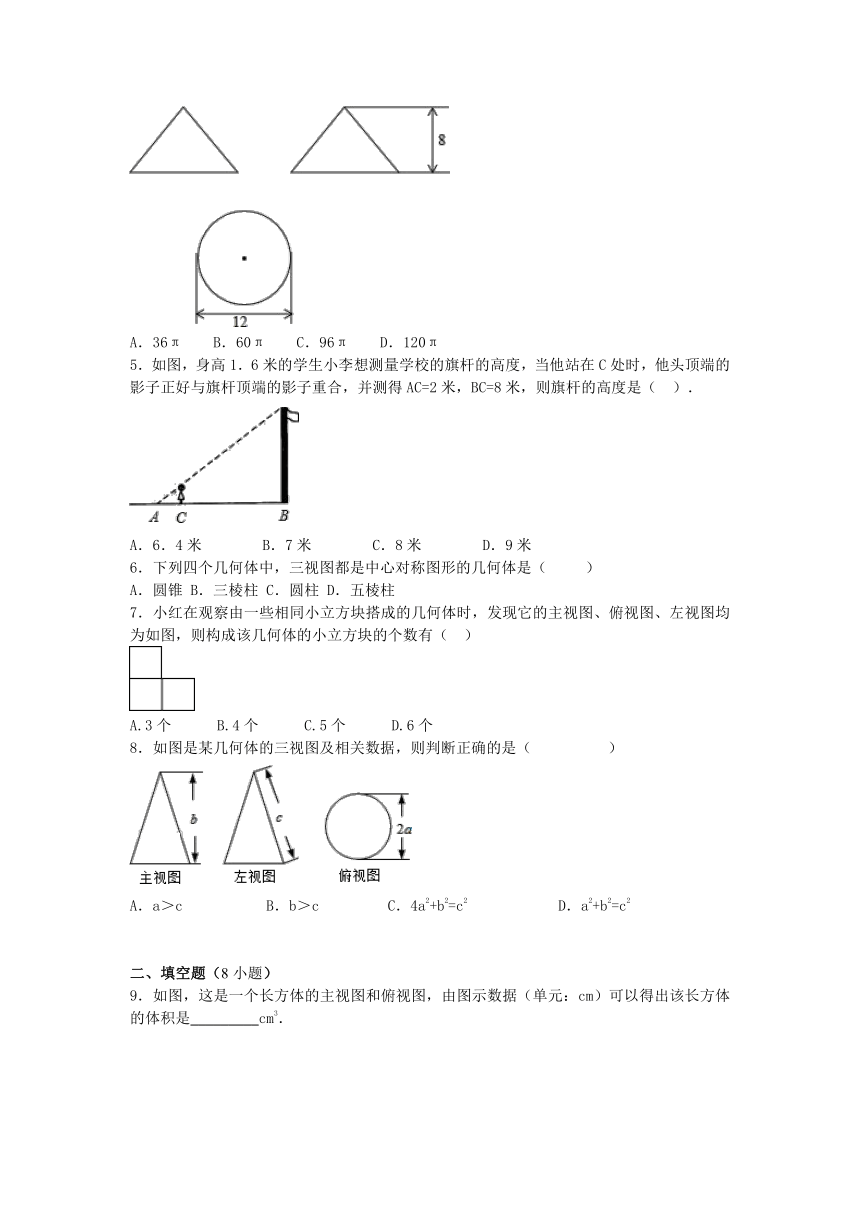
1.在下面的四个几何体中,左视图与主视图不相同的几何体是
(
)
2.下图由几个相同的小正方体搭成一个几何体,它的俯视图是
(
)
A.
B.
C.
D.
3.如图是由八个小正方形搭成的几何体的俯视图,小正方形中的数字表示该位置上的小正方体的个数,则这个几何体的左视图是(
)
4.如图是某几何体的三视图,则该几何体的全面积是(
).
A.36π
B.60π
C.96π
D.120π
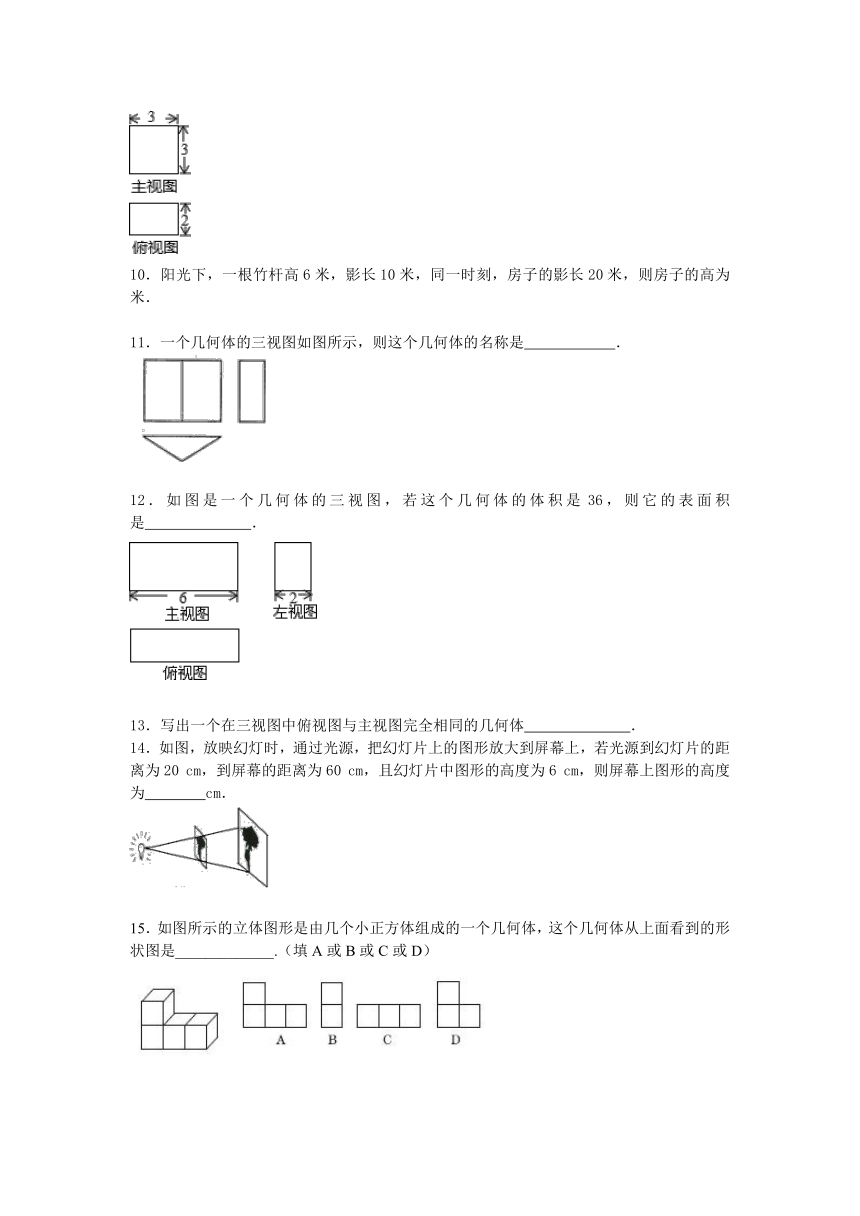
5.如图,身高1.6米的学生小李想测量学校的旗杆的高度,当他站在C处时,他头顶端的影子正好与旗杆顶端的影子重合,并测得AC=2米,BC=8米,则旗杆的高度是(
).
A.6.4米
B.7米
C.8米
D.9米
6.下列四个几何体中,三视图都是中心对称图形的几何体是(
)
A.圆锥
B.三棱柱
C.圆柱
D.五棱柱
7.小红在观察由一些相同小立方块搭成的几何体时,发现它的主视图、俯视图、左视图均为如图,则构成该几何体的小立方块的个数有(
)
A.3个
B.4个
C.5个
D.6个
8.如图是某几何体的三视图及相关数据,则判断正确的是(
)
A.a>c
B.b>c
C.4a2+b2=c2
D.a2+b2=c2
二、填空题(8小题)
9.如图,这是一个长方体的主视图和俯视图,由图示数据(单元:cm)可以得出该长方体的体积是_________cm3.
10.阳光下,一根竹杆高6米,影长10米,同一时刻,房子的影长20米,则房子的高为
米.
11.一个几何体的三视图如图所示,则这个几何体的名称是
.
12.如图是一个几何体的三视图,若这个几何体的体积是36,则它的表面积是
.
13.写出一个在三视图中俯视图与主视图完全相同的几何体
.
14.如图,放映幻灯时,通过光源,把幻灯片上的图形放大到屏幕上,若光源到幻灯片的距离为20
cm,到屏幕的距离为60
cm,且幻灯片中图形的高度为6
cm,则屏幕上图形的高度为
cm.
15.如图所示的立体图形是由几个小正方体组成的一个几何体,这个几何体从上面看到的形状图是_____________.(填A或B或C或D)
16.三棱柱的三视图如图所示,△EFG中,EF=8cm,EG=12cm,∠EGF=30°,则AB的长为_________cm.
三、作图
17.三根垂直地面的木杆甲、乙、丙,在路灯下乙、丙的影子如图所示.试确定路灯灯泡的位置,再作出甲的影子.(不写作法,保留作图痕迹)
四、解答题(6小题)
18.由大小相同的小立方块搭成的几何体,请在下图的方格中画出该几何体的三视图.
19.如图,AB和DE是直立在地面上的两根立柱.AB=5m,某一时刻AB在阳光下的投影BC=3m.
(1)请你在图中画出此时DE在阳光下的投影;
(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为6m,请你计算DE的长.
20.图(1)是一个蒙古包的照片,这个蒙古包可以近似看成是圆锥和圆柱组成的几何体,如图(2)所示.
(1)请画出这个几何体的俯视图;
(2)图(3)是这个几何体的正面示意图,已知蒙古包的顶部离地面的高度EO1=6米,圆柱部分的高OO1=4米,底面圆的直径BC=8米,求∠EAO的度数(结果精确到0.1°).
21.为了加强视力保护意识,小明想在长为4.3米,宽为3.2米的书房里挂一张测试距离为5米的视力表.在一次课题学习课上,小明向全班同学征集“解决空间过小,如何放置视力表问题”的方案,其中甲、乙、丙三位同学设计的方案新颖,构思巧妙.
(1)甲生的方案:如图1,将视力表挂在墙ABEF和墙ADGF的夹角处,被测试人站立在对角线AC上,问:甲生的设计方案是否可行?请说明理由.
(2)乙生的方案:如图2,将视力表挂在墙CDGH上,在墙ABEF上挂一面足够大的平面镜,根据平面镜成像原理课计算得到:测试线应画在距离墙ABEF
米处.
(3)丙生的方案:如图3,根据测试距离为5m的大视力表制作一个测试距离为3m的小视力表.图中的△ADF∽△ABC,如果大视力表中“E”的长是3.5cm,那么小视力表中相应的“E”的长是多少cm?
22.画图:⑴马小虎准备制作一个封闭的正方体盒子,他先用5个大小一样的正方形制成如下图所示的拼接图形(实线部分),经折叠后发现还少一个面,请你在右图中的拼接图形上再接一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子。
(注:①只需添加一个符合要求的正方形;②添加的正方形用阴影表示。)
⑵如图是一些小正方块所搭几何体的俯视图,小正方块中的数字表示该位置的小方块的个数,请画出这个几何体的主视图和左视图:
23.如图1,点O为直线AB上一点,过点O作射线OC,使∠AOC=60°.将一把直角三角尺的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方,其中∠OMN=30°。
(1)将图1中的三角尺绕点O顺时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC,求∠CON的度数;
(2)将图1中的三角尺绕点O按每秒10°的速度沿顺时针方向旋转一周,在旋转的过程中,在第
秒时,边MN恰好与射线OC平行;在第
秒时,直线ON恰好平分锐角∠AOC。(直接写出结果);
(3)将图1中的三角尺绕点O顺时针旋转至图3,使ON在∠AOC的内部,请探究∠AOM与∠NOC之间的数量关系,并说明理由.
参考答案
1.B.
2.D.
3.D.
4.C.
5.C.
6.C.
7.B.
8.D.
9.18
10.12
11.直三棱柱.
12.72.
13.球或正方体(答案不唯一).
14.18
15.C
16.6.
17.略
18.略
19.(1)略;(2)12m.
20.(1)略;(2)26.6°.
21.(1)可行;(2)米;(3)2.1cm
22.略
23.(1)已知∠AOC=60°,
所以∠BOC=120°,
又OM平分∠BOC,∠COM=∠BOC=60°
所以∠CON=∠COM+90°=150°
(2)当直线ON与OA重合时,MN恰好与射线OC平行,
∴∠AOM=90°,
由题意得,10t=90°
∴t=9
∵∠ONM=60°
∴当∠COM=30°时,MN恰好与射线OC平行
∴∠NOM=270°
由题意得,10t=270°
∴t=27
延长NO,
∵∠BOC=120°
∴∠AOC=60°,
当直线ON恰好平分锐角∠AOC,
∴∠AOD=∠COD=30°,
即顺时针旋转300°时NO延长线平分∠AOC,
由题意得,10t=300°
∴t=30,
当NO平分∠AOC,
∴∠NOR=30°,
即顺时针旋转120°时NO平分∠AOC,
∴10t=120°,
∴t=12,
∴t=12或30;
(3)因为∠MON=90°,∠AOC=60°,
所以∠AOM=90°-∠AON
∠NOC=60°-∠AON
所以∠AOM-∠NOC=(90°-∠AON)-(60°-∠AON)=30°,
所以∠AOM与∠NOC之间的数量关系为:∠AOM-∠NOC=30°
投影与视图
同步测试
一、选择题(8小题)
1.在下面的四个几何体中,左视图与主视图不相同的几何体是
(
)
2.下图由几个相同的小正方体搭成一个几何体,它的俯视图是
(
)
A.
B.
C.
D.
3.如图是由八个小正方形搭成的几何体的俯视图,小正方形中的数字表示该位置上的小正方体的个数,则这个几何体的左视图是(
)
4.如图是某几何体的三视图,则该几何体的全面积是(
).
A.36π
B.60π
C.96π
D.120π
5.如图,身高1.6米的学生小李想测量学校的旗杆的高度,当他站在C处时,他头顶端的影子正好与旗杆顶端的影子重合,并测得AC=2米,BC=8米,则旗杆的高度是(
).
A.6.4米
B.7米
C.8米
D.9米
6.下列四个几何体中,三视图都是中心对称图形的几何体是(
)
A.圆锥
B.三棱柱
C.圆柱
D.五棱柱
7.小红在观察由一些相同小立方块搭成的几何体时,发现它的主视图、俯视图、左视图均为如图,则构成该几何体的小立方块的个数有(
)
A.3个
B.4个
C.5个
D.6个
8.如图是某几何体的三视图及相关数据,则判断正确的是(
)
A.a>c
B.b>c
C.4a2+b2=c2
D.a2+b2=c2
二、填空题(8小题)
9.如图,这是一个长方体的主视图和俯视图,由图示数据(单元:cm)可以得出该长方体的体积是_________cm3.
10.阳光下,一根竹杆高6米,影长10米,同一时刻,房子的影长20米,则房子的高为
米.
11.一个几何体的三视图如图所示,则这个几何体的名称是
.
12.如图是一个几何体的三视图,若这个几何体的体积是36,则它的表面积是
.
13.写出一个在三视图中俯视图与主视图完全相同的几何体
.
14.如图,放映幻灯时,通过光源,把幻灯片上的图形放大到屏幕上,若光源到幻灯片的距离为20
cm,到屏幕的距离为60
cm,且幻灯片中图形的高度为6
cm,则屏幕上图形的高度为
cm.
15.如图所示的立体图形是由几个小正方体组成的一个几何体,这个几何体从上面看到的形状图是_____________.(填A或B或C或D)
16.三棱柱的三视图如图所示,△EFG中,EF=8cm,EG=12cm,∠EGF=30°,则AB的长为_________cm.
三、作图
17.三根垂直地面的木杆甲、乙、丙,在路灯下乙、丙的影子如图所示.试确定路灯灯泡的位置,再作出甲的影子.(不写作法,保留作图痕迹)
四、解答题(6小题)
18.由大小相同的小立方块搭成的几何体,请在下图的方格中画出该几何体的三视图.
19.如图,AB和DE是直立在地面上的两根立柱.AB=5m,某一时刻AB在阳光下的投影BC=3m.
(1)请你在图中画出此时DE在阳光下的投影;
(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为6m,请你计算DE的长.
20.图(1)是一个蒙古包的照片,这个蒙古包可以近似看成是圆锥和圆柱组成的几何体,如图(2)所示.
(1)请画出这个几何体的俯视图;
(2)图(3)是这个几何体的正面示意图,已知蒙古包的顶部离地面的高度EO1=6米,圆柱部分的高OO1=4米,底面圆的直径BC=8米,求∠EAO的度数(结果精确到0.1°).
21.为了加强视力保护意识,小明想在长为4.3米,宽为3.2米的书房里挂一张测试距离为5米的视力表.在一次课题学习课上,小明向全班同学征集“解决空间过小,如何放置视力表问题”的方案,其中甲、乙、丙三位同学设计的方案新颖,构思巧妙.
(1)甲生的方案:如图1,将视力表挂在墙ABEF和墙ADGF的夹角处,被测试人站立在对角线AC上,问:甲生的设计方案是否可行?请说明理由.
(2)乙生的方案:如图2,将视力表挂在墙CDGH上,在墙ABEF上挂一面足够大的平面镜,根据平面镜成像原理课计算得到:测试线应画在距离墙ABEF
米处.
(3)丙生的方案:如图3,根据测试距离为5m的大视力表制作一个测试距离为3m的小视力表.图中的△ADF∽△ABC,如果大视力表中“E”的长是3.5cm,那么小视力表中相应的“E”的长是多少cm?
22.画图:⑴马小虎准备制作一个封闭的正方体盒子,他先用5个大小一样的正方形制成如下图所示的拼接图形(实线部分),经折叠后发现还少一个面,请你在右图中的拼接图形上再接一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子。
(注:①只需添加一个符合要求的正方形;②添加的正方形用阴影表示。)
⑵如图是一些小正方块所搭几何体的俯视图,小正方块中的数字表示该位置的小方块的个数,请画出这个几何体的主视图和左视图:
23.如图1,点O为直线AB上一点,过点O作射线OC,使∠AOC=60°.将一把直角三角尺的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方,其中∠OMN=30°。
(1)将图1中的三角尺绕点O顺时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC,求∠CON的度数;
(2)将图1中的三角尺绕点O按每秒10°的速度沿顺时针方向旋转一周,在旋转的过程中,在第
秒时,边MN恰好与射线OC平行;在第
秒时,直线ON恰好平分锐角∠AOC。(直接写出结果);
(3)将图1中的三角尺绕点O顺时针旋转至图3,使ON在∠AOC的内部,请探究∠AOM与∠NOC之间的数量关系,并说明理由.
参考答案
1.B.
2.D.
3.D.
4.C.
5.C.
6.C.
7.B.
8.D.
9.18
10.12
11.直三棱柱.
12.72.
13.球或正方体(答案不唯一).
14.18
15.C
16.6.
17.略
18.略
19.(1)略;(2)12m.
20.(1)略;(2)26.6°.
21.(1)可行;(2)米;(3)2.1cm
22.略
23.(1)已知∠AOC=60°,
所以∠BOC=120°,
又OM平分∠BOC,∠COM=∠BOC=60°
所以∠CON=∠COM+90°=150°
(2)当直线ON与OA重合时,MN恰好与射线OC平行,
∴∠AOM=90°,
由题意得,10t=90°
∴t=9
∵∠ONM=60°
∴当∠COM=30°时,MN恰好与射线OC平行
∴∠NOM=270°
由题意得,10t=270°
∴t=27
延长NO,
∵∠BOC=120°
∴∠AOC=60°,
当直线ON恰好平分锐角∠AOC,
∴∠AOD=∠COD=30°,
即顺时针旋转300°时NO延长线平分∠AOC,
由题意得,10t=300°
∴t=30,
当NO平分∠AOC,
∴∠NOR=30°,
即顺时针旋转120°时NO平分∠AOC,
∴10t=120°,
∴t=12,
∴t=12或30;
(3)因为∠MON=90°,∠AOC=60°,
所以∠AOM=90°-∠AON
∠NOC=60°-∠AON
所以∠AOM-∠NOC=(90°-∠AON)-(60°-∠AON)=30°,
所以∠AOM与∠NOC之间的数量关系为:∠AOM-∠NOC=30°
