12.2.5全等三角形条件(5)
图片预览





文档简介
课件15张PPT。12.2.5三角形全等的条件(5) 1、目前,我们已经学习过了几种
判定三角形全等的方法?你能说全面吗?它们对于直角三角形也适用吗?
为什么?2、符合下列各条件的直角三角形全等吗? (1)已知两条直角边;
(2)已知一锐角和直角边;
(3)已知一锐角和一斜边;
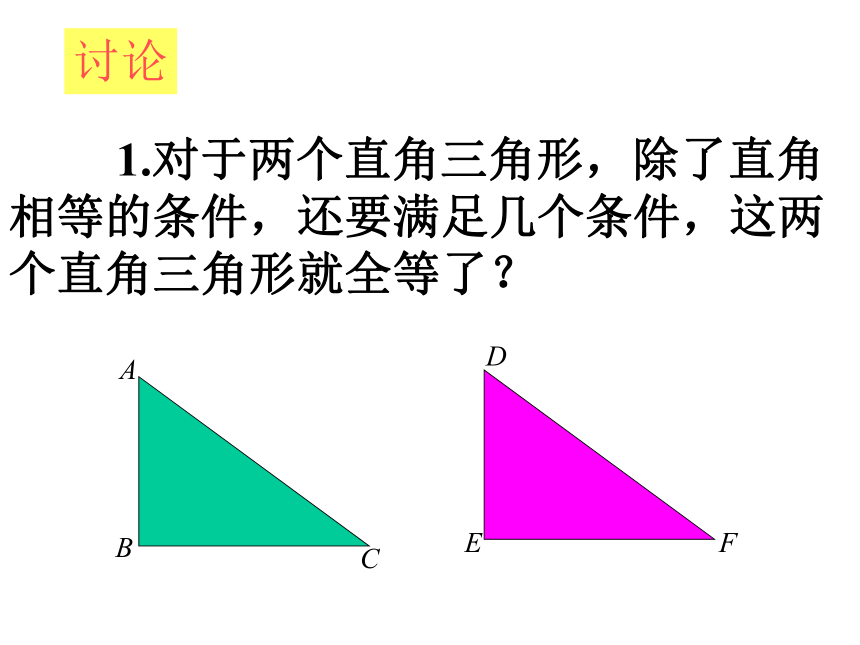
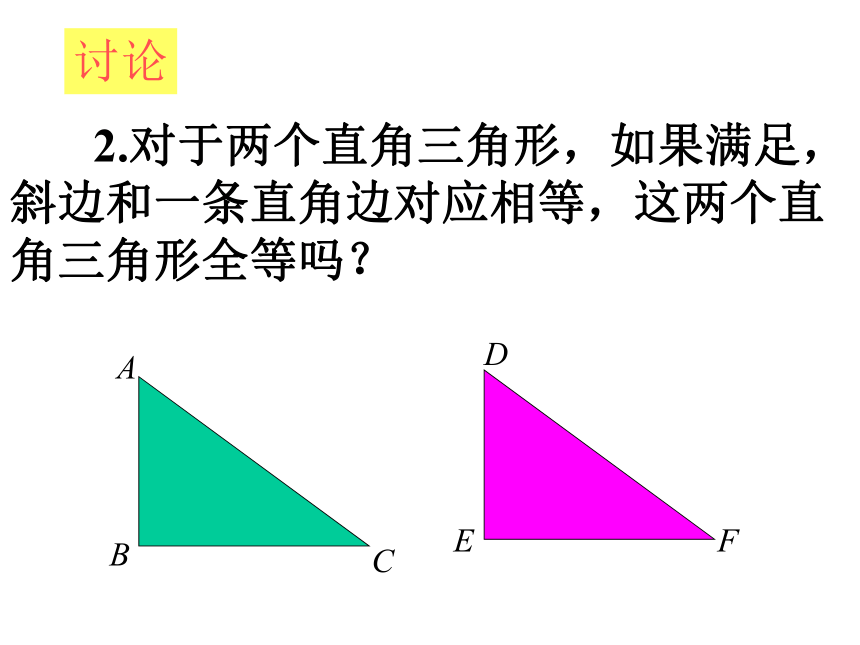
(4)已知一直角边和斜边。复习:问题: (1)舞台背景的形状是两个直角三角形,为了美观,工作人员想知道这两个直角三角形是否全等,但每个三角形都有一条直角边被花盆遮住无法测量,怎么办呢?(2)如果他带的测量工具只是一把卷尺时呢? (3)工作人员是这样做的,他测量了每个三角形没有被遮住的直角边和斜边,发现它们分别对应相等,于是他就肯定“两个直角三角形是全等的”.你相信他的结论吗? 1.对于两个直角三角形,除了直角相等的条件,还要满足几个条件,这两个直角三角形就全等了?讨论ABCDEF 2.对于两个直角三角形,如果满足,斜边和一条直角边对应相等,这两个直角三角形全等吗?讨论ABCDEF探究1 任意画出一个Rt△ABC,
使∠C=900,再画一个Rt△A/B/C/,
使∠C/=900 ,A/B/=AB,B/C/=BC,
把画好的Rt△A/B/C/剪下,放到
Rt△ABC上,它们全等吗? 画一个Rt△A/B/C/,使∠C/=900 ,A/B/=AB,B/C/=BC:1、画∠DC/ E= 900 .2、在射线C/ D上截取C/B/=CB.4、连结B/A/. △A/B/C/就是所要画的三角形.问:通过实验可以发现什么事实?3、以B/为圆心,AB为半径画弧,交射线C/ E于点A/. 有斜边和一条直角边
对应相等的两个直角三角
形全等(简写成“斜边、
直角边”或“HL”).探究反映的规律是:例题讲解:变式:(1)你还能找到其他的全等三角形吗?
(2)还可以得到哪些线段相等?O1.如图,AB⊥BC,AD⊥DC,
AB=AD.
求证∠1=∠2 .试一试我 会 了 2.如图,C是路段AB的中点,两人 从C同时出发,以相同的速度分别 沿两条直线行走,并同时到达D,E两地,DA⊥AB,EB⊥AB,D,E与路段AB的距离相等吗?为什么?小试牛刀3.如图,AB=CD,AE⊥BC,
DF⊥BC,CE=BF.
求证:AE=DF. 通过这节课的学习,你有什么收获和体会?还有什么疑问吗?好汉回头必做题: 习题12.2 6 ,7 ;
选做题:课外思考实践:
尽量画出两个全等的直角三角形所拼接的图形,并尝试寻求这两个直角三角形全等的条件。 推荐作业谢谢合作,再见!Bye-bye
判定三角形全等的方法?你能说全面吗?它们对于直角三角形也适用吗?
为什么?2、符合下列各条件的直角三角形全等吗? (1)已知两条直角边;
(2)已知一锐角和直角边;
(3)已知一锐角和一斜边;
(4)已知一直角边和斜边。复习:问题: (1)舞台背景的形状是两个直角三角形,为了美观,工作人员想知道这两个直角三角形是否全等,但每个三角形都有一条直角边被花盆遮住无法测量,怎么办呢?(2)如果他带的测量工具只是一把卷尺时呢? (3)工作人员是这样做的,他测量了每个三角形没有被遮住的直角边和斜边,发现它们分别对应相等,于是他就肯定“两个直角三角形是全等的”.你相信他的结论吗? 1.对于两个直角三角形,除了直角相等的条件,还要满足几个条件,这两个直角三角形就全等了?讨论ABCDEF 2.对于两个直角三角形,如果满足,斜边和一条直角边对应相等,这两个直角三角形全等吗?讨论ABCDEF探究1 任意画出一个Rt△ABC,
使∠C=900,再画一个Rt△A/B/C/,
使∠C/=900 ,A/B/=AB,B/C/=BC,
把画好的Rt△A/B/C/剪下,放到
Rt△ABC上,它们全等吗? 画一个Rt△A/B/C/,使∠C/=900 ,A/B/=AB,B/C/=BC:1、画∠DC/ E= 900 .2、在射线C/ D上截取C/B/=CB.4、连结B/A/. △A/B/C/就是所要画的三角形.问:通过实验可以发现什么事实?3、以B/为圆心,AB为半径画弧,交射线C/ E于点A/. 有斜边和一条直角边
对应相等的两个直角三角
形全等(简写成“斜边、
直角边”或“HL”).探究反映的规律是:例题讲解:变式:(1)你还能找到其他的全等三角形吗?
(2)还可以得到哪些线段相等?O1.如图,AB⊥BC,AD⊥DC,
AB=AD.
求证∠1=∠2 .试一试我 会 了 2.如图,C是路段AB的中点,两人 从C同时出发,以相同的速度分别 沿两条直线行走,并同时到达D,E两地,DA⊥AB,EB⊥AB,D,E与路段AB的距离相等吗?为什么?小试牛刀3.如图,AB=CD,AE⊥BC,
DF⊥BC,CE=BF.
求证:AE=DF. 通过这节课的学习,你有什么收获和体会?还有什么疑问吗?好汉回头必做题: 习题12.2 6 ,7 ;
选做题:课外思考实践:
尽量画出两个全等的直角三角形所拼接的图形,并尝试寻求这两个直角三角形全等的条件。 推荐作业谢谢合作,再见!Bye-bye
