大庆市肇源县2016-2017学年八年级(五四制)上学期期末考试数学试卷(含答案)
文档属性
| 名称 | 大庆市肇源县2016-2017学年八年级(五四制)上学期期末考试数学试卷(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 275.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-01-10 00:00:00 | ||
图片预览




文档简介
2016~2017学年度上学期期末质量监测
初三数学试题
题号
一
二
三
总分
21
22
23
24
25
26
27
28
得分
考生注意:1.考试时间120分钟。2.全卷共三道大题,共25个小题,总分120分。
一、选择题(本大题共10小题,每小题3分,共30分.在每小题所给出的选项中,只有一项是符合题目要求的,请将正确的选项书写在相应的位置上)
1.若a<0,则下列不等式不成立的是( )
A.a+5<a+7 B.5a>7a C.5-a<7-a D.
2.下列从左到右的变形是因式分解的是( )
A.(x+1)(x-1)=x2-1 B.(a-b)(m-n)=(b-a)(n-m)
C.ab-a-b+1=(a-1)(b-1) D.m2-2m-3=m(m-2-)
3.方程的解为( )
A.2 B.1 C.-2 D.-1
4.下列图形中,既是轴对称图形图形又是中心对称图形的是( )
A B C D
5. 等腰三角形的一个角是80°,则它的顶角的度数是 ( )
A.80° B.80°或20° C.80°或50° D.20°
6.若以A(-1,0),B(2,0),C(0,1)三点为顶点画平行四边形,则第四个顶点不可能在 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.若一个正多边形的每个内角等于120°,则这个多边形是( )边形。
A.8 B.7 C.6 D.5
9题图 10题图
8.去分母解关于x的方程时产生增根,则m的值为 ( )
A.m=1 B. m=-1 C. m=2 D. m无法求出
9.如图,平行四边形ABCD的对角线相交于点O,且AB≠AD,过O作OE⊥BD交BC于点E.若△CDE的周长为10,则AB+AD的值是( )
A.10 B.15 C.25 D.30
10.∠C=90°,AC=BC,AD平分∠CAB,交BC于点D,DE⊥AB于点E,且AB=10,则△EDB的周长是( )
A.4 B.6 C.8 D.10
二、填空题(本大题共10小题,每空3分,共30分.不需写出解答过程,请把答案直接填写在相应的位置上)
11.分解因式:x2y-y3=____________ 。
12.当________时,分式值为0。
13.如图,已知函数y=3x+b和y=ax-3的图象交于点P(-2,-5),则根据图象可得不等式3x+b>ax-3的解集是________。
13题图 14题图
14.如图,面积为12cm2的△ABC沿BC方向平移至△DEF位置,平移的距离是边BC长的两倍,则图中的四边形ACED的面积是______cm2。
15.某工厂现在平均每天比原计划多生产50台机器,现在生产600台机器所需要时间与原计划生产450台机器所需时间相同,现在平均每天生产________台机器。
16.若 ABCD中,∠A和∠B是一对邻角,如果∠A︰∠B=4︰5,那么∠A=____度。
17.已知关于x的方程3x+a=x-7的根是正数,则a的取值范围是 。
18.直角三角形三边长分别为x、3、4,则x= 。
19.,则的取值范围是_______。
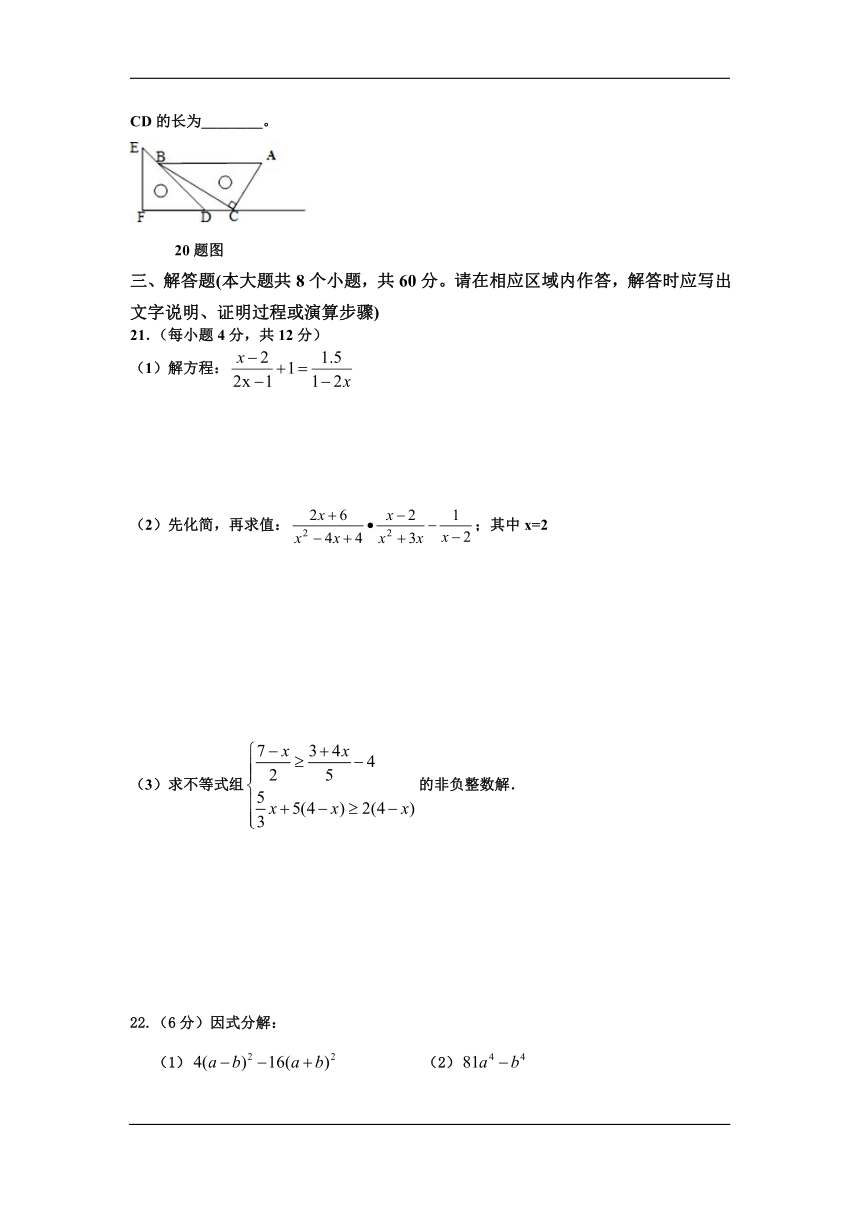
20.如图一副直角三角板放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,AC=5,CD的长为________。
20题图
三、解答题(本大题共8个小题,共60分。请在相应区域内作答,解答时应写出文字说明、证明过程或演算步骤)
21.(每小题4分,共12分)
(1)解方程:
(2)先化简,再求值:;其中x=2
WWW.ziyuanku.com
(3)求不等式组的非负整数解.
Ziyuanku.com
22.(6分)因式分解:
(1) (2)
$来&源:ziyuanku.com
23.(6分)如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,
点A的坐标为(2,4),请解答下列问题:(1)画出△ABC关于x轴对称的△A1B1C1,
并写出点A1的坐标;
(2)画出△A1B1C1绕原点O旋转180°,后得到的△A2B2C2,并写出点A2的坐标.
24.(6分)如图1,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.
求证:BE=CE;
25.(7分)大庆市移动通讯公司开设了两种通讯业务:“全球通”使用者先缴50元/月基础 费,然后每通话1分钟,再付0.4元;“神州行”不缴月基础费,每通话1分钟,付话费0.6元(这里均指市内通话)。若一个月内通话时间为x分钟,两种通讯方式的费用分别为y1元和y2元。
(1)写出y1、y2与x的关系式。
(2)请你根据用户通讯时间的多少,给出经济实惠的选择建议。
26.(7分)为了提高产品的附加值,某公司计划将研发生产的1200件新产品进行精加工后再投放市场.现有甲、乙两个工厂都具备加工能力,公司派出相关人员分别到这两间工厂了解情况,获得如下信息:
信息一:甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天;
信息二:乙工厂每天加工的数量是甲工厂每天加工数量的1.5倍。
根据以上信息,求甲、乙两个工厂每天分别能加工多少件新产品?
27.(8分)如图,OC是∠AOB的平分线,点P为OC上一点,若∠PDO+∠PEO=180°,试判断PD和PE的大小关系,并说明理由.
28. (8分)如图,在四边形ABCD中,AD平行且等于BC,AB平行且等于DC,AD⊥AB,E是AB边的中点,沿EC对折矩形ABCD,使B点落在点P处,折痕为EC,连结AP并延长AP交CD于F点.
(1)求证:四边形AECF为平行四边形;
(2)若△AEP是等边三角形,连结BP,求证:△APB≌△EPC;
(3)若四边形ABCD的边AB=6,BC=4,求△APB的面积.
2016~2017学年度上学期期末质量监测
初三数学试题参考答案
一、选择题
1
2
3
4
5
6
7
8
9
10
A
C
A
B
资*源%库 ziyuanku.comC
C
C
B
A
D
二.填空题
11.y(x-y)(x+y) 12.x=-1 13.x>-2 14.48 15.200
16.80 17. a<-7 18.5或 19.m< 3 20.
解答题
Ziyuanku.com21.(1)解得X= ----------------------------------3分
检验-----------------------------------------4分
资*源%库(2) , ------------------------------------3分
----------------------------------------4分
(3)不等式组的解集为, 所以不等式组的非负整数解为: 0,l,2,3,4,5.------------------------4分
22.(1)
资*源%库 原式=--------------------------------2分
----------------------------------------------------------3分
23.
(图形4分,两点2分)
24.证明:(1)∵AB=AC,D是BC的中点,
∴∠BAE=∠EAC,
在△ABE和△ACE中,,
∴△ABE≌△ACE(SAS),
∴BE=CE;-------------------6分
25题由题意可知y1=50+0.4x---------------------2分
y2=0.6x------------------------3分
当y1= y2 时,即50+0.4x=0.6x,解得x=250
当y1> y2 时,即50+0.4x>0.6x,解得x<250
当y1< y2 时,即50+0.4x<0.6x,解得x>250 ----- 6分
∴当用户每月通话时间少于250分钟,选“神州行”当多于250分钟选“全球通”,当通话时间为250分钟时,
选择哪种方式都一样。-------------7分
26题解:设甲工厂每天加工x件产品,则乙工厂每天加工1.5x件产品,--1分
依题意得:
-----------------------------------3分
解得:x=40-------------------------------------------5分
经检验:x=40是原方程的根,所以1.5x=60--------6分
答:甲工厂每天加工40件产品,乙工厂每天加工60件产品.-------------7分
27.解:DP=EP
作PF⊥OA于点F,PG⊥OB于点G.∠DFP=∠EGP=90°
∵O C是为角平分线
∴PF=PG
∵∠PDO+∠PEO=180°
∠PDO+∠FDP=180°
∴∠PEO=∠FDP
∴△DPF≌△EPG(ASA).
DP=EP. -------------------------------8分
方法二:
1分
8分
28.如图,在矩形ABCD中,E是AB边的中点,沿EC对折矩形ABCD,使B点落在点P处,折痕为EC,连结AP并延长AP交CD于F点.
(1)求证:四边形AECF为平行四边形;
(2)若△AEP是等边三角形,连结BP,求证:△APB≌△EPC;
(3)若矩形ABCD的边AB=6,BC=4,求△APB的面积.
(1)证明:由折叠得到BE=PE,EC⊥PB,又E为AB中点,
∴AE=PE=EB,
∴∠APB=90°,
即BP⊥AF,
∴AF∥EC,
∴四边形AECF为平行四边形;--------------------------3分
(2)由△AEP是等边三角形得∠AEP=60°,进而由折叠可得∠PEC=PAB=60°,又AP=PE,∴Rt△ABP≌Rt△EBC;-------------------------------6分
(3)在Rt△EBC中,EB=3,BC=4,EC=5,∵S△EBC=EB?BC=EC?BQ,∴BQ=,由折叠得:BP=2BQ=,在Rt△ABP中,AB=6,BP=,由勾股定理得AP=,则S△APB=AP?BP=××=.
-------------------------------8分
初三数学试题
题号
一
二
三
总分
21
22
23
24
25
26
27
28
得分
考生注意:1.考试时间120分钟。2.全卷共三道大题,共25个小题,总分120分。
一、选择题(本大题共10小题,每小题3分,共30分.在每小题所给出的选项中,只有一项是符合题目要求的,请将正确的选项书写在相应的位置上)
1.若a<0,则下列不等式不成立的是( )
A.a+5<a+7 B.5a>7a C.5-a<7-a D.
2.下列从左到右的变形是因式分解的是( )
A.(x+1)(x-1)=x2-1 B.(a-b)(m-n)=(b-a)(n-m)
C.ab-a-b+1=(a-1)(b-1) D.m2-2m-3=m(m-2-)
3.方程的解为( )
A.2 B.1 C.-2 D.-1
4.下列图形中,既是轴对称图形图形又是中心对称图形的是( )
A B C D
5. 等腰三角形的一个角是80°,则它的顶角的度数是 ( )
A.80° B.80°或20° C.80°或50° D.20°
6.若以A(-1,0),B(2,0),C(0,1)三点为顶点画平行四边形,则第四个顶点不可能在 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.若一个正多边形的每个内角等于120°,则这个多边形是( )边形。
A.8 B.7 C.6 D.5
9题图 10题图
8.去分母解关于x的方程时产生增根,则m的值为 ( )
A.m=1 B. m=-1 C. m=2 D. m无法求出
9.如图,平行四边形ABCD的对角线相交于点O,且AB≠AD,过O作OE⊥BD交BC于点E.若△CDE的周长为10,则AB+AD的值是( )
A.10 B.15 C.25 D.30
10.∠C=90°,AC=BC,AD平分∠CAB,交BC于点D,DE⊥AB于点E,且AB=10,则△EDB的周长是( )
A.4 B.6 C.8 D.10
二、填空题(本大题共10小题,每空3分,共30分.不需写出解答过程,请把答案直接填写在相应的位置上)
11.分解因式:x2y-y3=____________ 。
12.当________时,分式值为0。
13.如图,已知函数y=3x+b和y=ax-3的图象交于点P(-2,-5),则根据图象可得不等式3x+b>ax-3的解集是________。
13题图 14题图
14.如图,面积为12cm2的△ABC沿BC方向平移至△DEF位置,平移的距离是边BC长的两倍,则图中的四边形ACED的面积是______cm2。
15.某工厂现在平均每天比原计划多生产50台机器,现在生产600台机器所需要时间与原计划生产450台机器所需时间相同,现在平均每天生产________台机器。
16.若 ABCD中,∠A和∠B是一对邻角,如果∠A︰∠B=4︰5,那么∠A=____度。
17.已知关于x的方程3x+a=x-7的根是正数,则a的取值范围是 。
18.直角三角形三边长分别为x、3、4,则x= 。
19.,则的取值范围是_______。
20.如图一副直角三角板放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,AC=5,CD的长为________。
20题图
三、解答题(本大题共8个小题,共60分。请在相应区域内作答,解答时应写出文字说明、证明过程或演算步骤)
21.(每小题4分,共12分)
(1)解方程:
(2)先化简,再求值:;其中x=2
WWW.ziyuanku.com
(3)求不等式组的非负整数解.
Ziyuanku.com
22.(6分)因式分解:
(1) (2)
$来&源:ziyuanku.com
23.(6分)如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,
点A的坐标为(2,4),请解答下列问题:(1)画出△ABC关于x轴对称的△A1B1C1,
并写出点A1的坐标;
(2)画出△A1B1C1绕原点O旋转180°,后得到的△A2B2C2,并写出点A2的坐标.
24.(6分)如图1,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.
求证:BE=CE;
25.(7分)大庆市移动通讯公司开设了两种通讯业务:“全球通”使用者先缴50元/月基础 费,然后每通话1分钟,再付0.4元;“神州行”不缴月基础费,每通话1分钟,付话费0.6元(这里均指市内通话)。若一个月内通话时间为x分钟,两种通讯方式的费用分别为y1元和y2元。
(1)写出y1、y2与x的关系式。
(2)请你根据用户通讯时间的多少,给出经济实惠的选择建议。
26.(7分)为了提高产品的附加值,某公司计划将研发生产的1200件新产品进行精加工后再投放市场.现有甲、乙两个工厂都具备加工能力,公司派出相关人员分别到这两间工厂了解情况,获得如下信息:
信息一:甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天;
信息二:乙工厂每天加工的数量是甲工厂每天加工数量的1.5倍。
根据以上信息,求甲、乙两个工厂每天分别能加工多少件新产品?
27.(8分)如图,OC是∠AOB的平分线,点P为OC上一点,若∠PDO+∠PEO=180°,试判断PD和PE的大小关系,并说明理由.
28. (8分)如图,在四边形ABCD中,AD平行且等于BC,AB平行且等于DC,AD⊥AB,E是AB边的中点,沿EC对折矩形ABCD,使B点落在点P处,折痕为EC,连结AP并延长AP交CD于F点.
(1)求证:四边形AECF为平行四边形;
(2)若△AEP是等边三角形,连结BP,求证:△APB≌△EPC;
(3)若四边形ABCD的边AB=6,BC=4,求△APB的面积.
2016~2017学年度上学期期末质量监测
初三数学试题参考答案
一、选择题
1
2
3
4
5
6
7
8
9
10
A
C
A
B
资*源%库 ziyuanku.comC
C
C
B
A
D
二.填空题
11.y(x-y)(x+y) 12.x=-1 13.x>-2 14.48 15.200
16.80 17. a<-7 18.5或 19.m< 3 20.
解答题
Ziyuanku.com21.(1)解得X= ----------------------------------3分
检验-----------------------------------------4分
资*源%库(2) , ------------------------------------3分
----------------------------------------4分
(3)不等式组的解集为, 所以不等式组的非负整数解为: 0,l,2,3,4,5.------------------------4分
22.(1)
资*源%库 原式=--------------------------------2分
----------------------------------------------------------3分
23.
(图形4分,两点2分)
24.证明:(1)∵AB=AC,D是BC的中点,
∴∠BAE=∠EAC,
在△ABE和△ACE中,,
∴△ABE≌△ACE(SAS),
∴BE=CE;-------------------6分
25题由题意可知y1=50+0.4x---------------------2分
y2=0.6x------------------------3分
当y1= y2 时,即50+0.4x=0.6x,解得x=250
当y1> y2 时,即50+0.4x>0.6x,解得x<250
当y1< y2 时,即50+0.4x<0.6x,解得x>250 ----- 6分
∴当用户每月通话时间少于250分钟,选“神州行”当多于250分钟选“全球通”,当通话时间为250分钟时,
选择哪种方式都一样。-------------7分
26题解:设甲工厂每天加工x件产品,则乙工厂每天加工1.5x件产品,--1分
依题意得:
-----------------------------------3分
解得:x=40-------------------------------------------5分
经检验:x=40是原方程的根,所以1.5x=60--------6分
答:甲工厂每天加工40件产品,乙工厂每天加工60件产品.-------------7分
27.解:DP=EP
作PF⊥OA于点F,PG⊥OB于点G.∠DFP=∠EGP=90°
∵O C是为角平分线
∴PF=PG
∵∠PDO+∠PEO=180°
∠PDO+∠FDP=180°
∴∠PEO=∠FDP
∴△DPF≌△EPG(ASA).
DP=EP. -------------------------------8分
方法二:
1分
8分
28.如图,在矩形ABCD中,E是AB边的中点,沿EC对折矩形ABCD,使B点落在点P处,折痕为EC,连结AP并延长AP交CD于F点.
(1)求证:四边形AECF为平行四边形;
(2)若△AEP是等边三角形,连结BP,求证:△APB≌△EPC;
(3)若矩形ABCD的边AB=6,BC=4,求△APB的面积.
(1)证明:由折叠得到BE=PE,EC⊥PB,又E为AB中点,
∴AE=PE=EB,
∴∠APB=90°,
即BP⊥AF,
∴AF∥EC,
∴四边形AECF为平行四边形;--------------------------3分
(2)由△AEP是等边三角形得∠AEP=60°,进而由折叠可得∠PEC=PAB=60°,又AP=PE,∴Rt△ABP≌Rt△EBC;-------------------------------6分
(3)在Rt△EBC中,EB=3,BC=4,EC=5,∵S△EBC=EB?BC=EC?BQ,∴BQ=,由折叠得:BP=2BQ=,在Rt△ABP中,AB=6,BP=,由勾股定理得AP=,则S△APB=AP?BP=××=.
-------------------------------8分
同课章节目录
