2017考前3个月(通用版)物理课件:知识专题2 力与物体的直线运动45张PPT
文档属性
| 名称 | 2017考前3个月(通用版)物理课件:知识专题2 力与物体的直线运动45张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2017-01-13 14:34:01 | ||
图片预览









文档简介
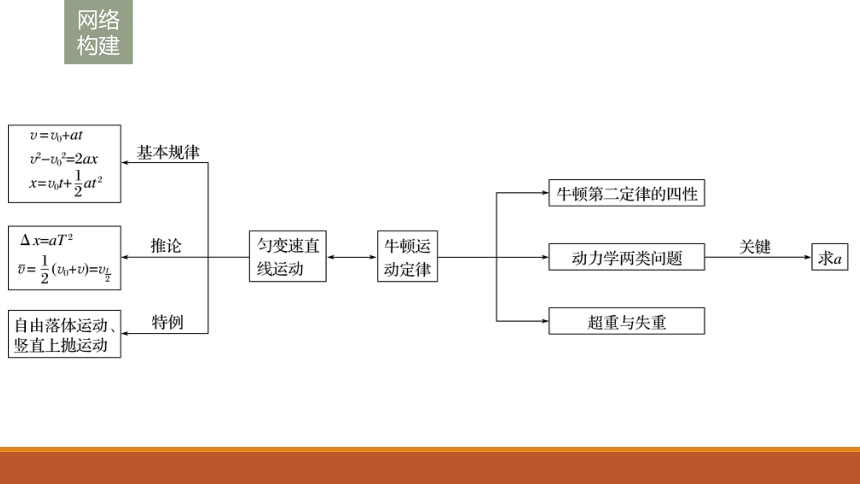
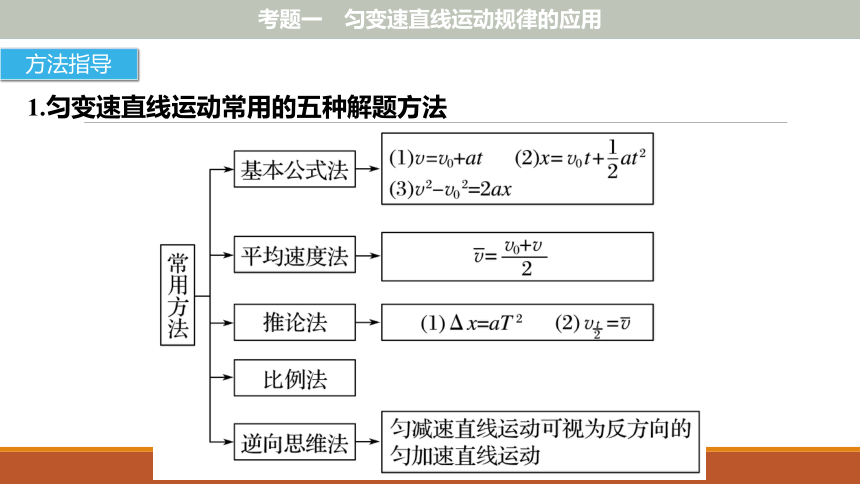
课件45张PPT。专题2 力与物体的直线运动知识专题网络构建考题二 运动学图象问题考题三 牛顿运动定律的应用栏目索引考题一 匀变速直线运动规律的应用考题四 “传送带”、“滑块-木板模型”问题考题一 匀变速直线运动规律的应用1.匀变速直线运动常用的五种解题方法方法指导2.追及问题的解题思路和技巧
(1)解题思路(2)解题技巧
①紧抓“一图三式”,即过程示意图、时间关系式、速度关系式和位移关系式.
②审题应抓住题目中的关键字眼,充分挖掘题目中的隐含条件,如“刚好”
“恰好”“最多”“至少”等,往往对应一个临界状态,满足相应的临界条件.③若被追赶的物体做匀减速运动,一定要注意追上前该物体是否已停止运动,另外还要注意最后对解的讨论分析.
3.处理刹车类问题的思路
先判断刹车时间t0= ,再进行分析计算.解析答案例1 如图1所示,云南省彝良县发生特大泥石流,一汽车停在小山坡底,司机突然发现在距坡底240 m的山坡处泥石流以8 m/s的初速度、0.4 m/s2的加速度匀加速倾泻而下,假设泥石流到达坡底后速率不变,在水平地面上做匀速直线运动.已知司机的反应时间为1 s,汽车启动后以0.5 m/s2的加速度一直做匀加速直线运动.试分析司机能否安全脱离.图1典例剖析解析 设泥石流到达坡底的时间为t1,速度为v1,
v1=v0+a1t1
解得:t1=20 s,v1=16 m/s
而汽车在t2=19 s的时间内发生的位移为:
速度为:v2=a2t2=9.5 m/s
假设再经时间t3,泥石流能够追上汽车,则有:因Δ<0,方程无解,所以泥石流无法追上汽车,司机能安全脱离.
答案 司机能安全脱离1.“蛟龙号”是我国首台自主研制的作业型深海载人潜水器,它是目前世界上下潜能力最强的潜水器.假设某次海试活动中,“蛟龙号”完成海底任务后竖直上浮,从上浮速度为v时开始计时,此后“蛟龙号”匀减速上浮,经过时间t上浮到海面,速度恰好减为零,则“蛟龙号”在t0(t0(1)看坐标轴:看清坐标轴所表示的物理量,明确因变量(纵轴表示的量)与自变量(横轴表示的量)之间的制约关系.
(2)看图象:识别两个相关量的变化趋势,从而分析具体的物理过程.
(3)看纵坐标、“斜率”和“面积”:v-t图象中根据坐标值、“斜率”和“面积”可分析速度、加速度和位移的大小、方向特点.x-t图象中根据坐标值、“斜率”可分析位移、速度的大小、方向特点.
(4)看交点:明确图线与图线的交点、图线与坐标轴的交点的物理意义.
(5)一注意:利用v-t图象分析两个物体的运动时,要注意两个物体的出发点,即注意它们是从同一位置出发,还是从不同位置出发.若从不同位置出发,要注意出发时两者的距离.例2 甲、乙两物体从同一地点同时开始沿同一方向运动,甲物体运动的v-t图象为两段直线,乙物体运动的v-t图象为两段半径相同的 圆弧曲线,如图3所示,图中t4=2t2,则在0~t4时间内,以下说法正确的是( )
A.甲物体的加速度不变
B.乙物体做曲线运动
C.两物体t1时刻相距最远,t4时刻相遇
D.甲物体的平均速度等于乙物体的平均速度解析典例剖析图3√解析 0~t2时间段内,甲做匀加速直线运动,t2~t4时间内甲物体做匀减速直线运动,故A错;
速度是矢量,在速度时间图象中,只能表示直线运动,B错;
在整个运动过程中,t3时刻两物体相距最远,C错;
在速度时间图象中,图线下面所包围的面积即为位移,可求知0~t4时间段内,位移相等,故平均速度相同,D对.3.如图4所示,x-t图象反映了甲、乙两车在同一条直线上行驶的位移随时间变化的关系,已知乙车做匀变速直线运动,其图线与t轴相切于10 s处,下列说法正确的是( )
A.5 s时两车速度相等
B.甲车的速度为4 m/s
C.乙车的加速度大小为1.6 m/s2
D.乙车的初位置在x0=80 m处解析34√[变式训练]图4√√解析 位移-时间图象的斜率等于速度,斜率大小越大,速度大小越大,则知5 s时乙车速度较大,故A错误.344.静止在光滑水平面上的物体,同时受到在同一直线
上的力F1、F2作用,F1、F2随时间变化的图象如图5
所示,则物体在0~2t时间内( )
A.离出发点越来越远
B.速度先变大后变小
C.速度先变小后变大
D.加速度先变大后变小
解析 由图线可知,物体受到的合力先减小后增大,加速度先减小后增大,速度一直变大,物体离出发点越来越远,选项A正确.√解析返回34图5 考题三 牛顿运动定律的应用方法指导1.动力学的两类基本问题
(1)由因推果——已知物体的受力情况,确定物体的运动情况.
(2)由果溯因——已知物体的运动情况,确定物体的受力情况.
桥梁:牛顿第二定律F=ma2.超重和失重现象的判断技巧
(1)从受力的角度判断:当物体所受向上的拉力(或支持力)大于重力时,物体处于超重状态,小于重力时处于失重状态,等于零时处于完全失重状态.
(2)从加速度的角度判断:当物体具有向上的加速度时处于超重状态,具有向下的加速度时处于失重状态,向下的加速度为重力加速度时处于完全失重状态.
(3)从速度变化的角度判断:物体向上加速或向下减速时,超重;物体向下加速或向上减速时,失重.3.瞬时性问题的处理
(1)牛顿第二定律是力的瞬时作用规律,加速度和力同时产生、同时变化、同时消失,分析物体在某一时刻的瞬时加速度,关键是分析该瞬时前后的受力情况及其变化.
(2)明确两种基本模型的特点:
①轻绳的形变可瞬时产生或恢复,故绳的弹力可以瞬时突变.
②轻弹簧(或橡皮绳)两端均连有物体时,形变恢复需较长时间,其弹力的大小与方向均不能突变.4.整体法和隔离法的优点及使用条件
(1)整体法:
①优点:研究对象减少,忽略物体之间的相互作用力,方程数减少,求解简捷.
②条件:连接体中各物体具有共同的加速度
(2)隔离法:
①优点:易看清各个物体具体的受力情况.
②条件:当系统内各物体的加速度不同时,一般采用隔离法;求连接体内各物体间的相互作用力时必须用隔离法.典例剖析例3 (2016·四川理综·10)避险车道是避免恶性交通事故的重要设施,由制动坡床和防撞设施等组成,如图6竖直平面内,制动坡床视为与水平面夹角为θ的斜面.一辆长12 m的载有货物的货车因刹车失灵从干道驶入制动坡床,当车速为23 m/s时,车尾位于制动坡床的底端,货物开始在车厢内向车头滑动,当货物在车厢内滑动了4 m时,车头距制动坡床顶端38 m,再过一段时间,货车停止.已知货车质量是货物质量的4倍,货物与车厢间的动摩擦因数为0.4;货车在制动坡床上运动受到的坡床阻力大小为货车和货物总重的0.44倍.货物与货车可分别视为小滑块和
平板,取cos θ=1,sin θ=0.1,g=10 m/s2.
求:图6(1)货物在车厢内滑动时加速度的大小和方向;
解析 设货物的质量为m,货物在车厢内滑动
过程中,货物与车厢的动摩擦因数μ=0.4,
受摩擦力大小为f,加速度大小为a1,则
f+mgsin θ=ma1 ①
f=μmgcos θ ②
联立①②并代入数据得a1=5 m/s2 ③
a1的方向沿制动坡床向下.
答案 5 m/s2 方向沿制动坡床向下解析答案(2)制动坡床的长度.解析答案解析 设货车的质量为M,车尾位于制动坡床底端时的车速为v=23 m/s.货物在车厢内开始滑动到车头距制动坡床顶端s0=38 m的过程中,用时为t,货物相对制动坡床的运动距离为s1,在车厢内滑动的距离s=4 m,货车的加速度大小为a2,货车相对制动坡床的运动距离为s2.货车受到制动坡床的阻力大小为F,F是货车和货物总重的k倍,k=0.44,货车长度l0=12 m,制动坡床的长度为l,则
Mgsin θ+F-f=Ma2 ④
F=k(m+M)g ⑤
⑥解析答案 ⑦
s=s1-s2 ⑧
l=l0+s0+s2 ⑨
联立①~⑨并代入数据得
l=98 m
答案 98 m5.为了让乘客乘车更为舒适,某探究小组设计了一种新的交通工具,乘客的座椅能随着坡度的变化而自动调整,使座椅始终保持水平,如图7所示,当此车加速上坡时,盘腿坐在座椅上的一位乘客( )
A.处于失重状态
B.不受摩擦力的作用
C.受到向前(水平向右)的摩擦力作用
D.所受力的合力竖直向上解析56√[变式训练]7图7解析 车加速上坡,车里的乘客与车相对静止,应该和车具有相同的加速度,方向沿斜坡向上,对乘客受力分析可知,乘客应受到竖直向下的重力,垂直水平面竖直向上的弹力和水平向右的摩擦力,三力合力沿斜面向上,B、D错误,C正确;
弹力大于重力,乘客处于超重状态,A错误.5676.如图8所示,A、B两小球分别连在弹簧两端,B端用绳子固定在倾角为30°的光滑斜面上,若不计弹簧质量,在绳子被剪断瞬间,A、B两球的加速度分别为( )图8解析√567解析 对A:在剪断绳子之前,A处于平衡状态,所以弹簧的拉力等于A的重力沿斜面的分力.在剪断上端的绳子的瞬间,绳子上的拉力立即减为零,而弹簧的伸长量没有来得及发生改变,故弹力不变仍等于A的重力沿斜面的分力.故A球的加速度为零;对B:在剪断绳子之前,对B球进行受力分析,B受到重力、弹簧对它斜向下的拉力、支持力及绳子的拉力,在剪断上端的绳子的瞬间,绳子上的拉力立即减为零,对B球进行受力分析,则B受到重力、弹簧斜向下的拉力、支持力.所以根据牛顿第二定律得5677.如图9所示用力F拉a、b、c三个物体在光滑水平面上运动,现在中间的物体b上加一块橡皮泥,它和中间的物体一起运动,且原拉力F不变,那么加上橡皮泥以后,两段绳的拉力FTa和FTb的变化情况是( )
A.FTa增大 B.FTb增大
C.FTa减小 D.FTb减小567图9解析√√返回567返回 考题四 “传送带”、“滑块-木板模型”问题方法指导1.传送带问题分析的要点是物体与传送带间的摩擦力,关注点是两个时刻:
(1)初始时刻物体相对于传送带的速度或滑动方向决定了该时刻摩擦力的方向.
(2)物体与传送带速度相等的时刻摩擦力的大小(或有无)、性质(滑动摩擦力或静摩擦力)或方向会发生改变.正确判断这两个时刻的摩擦力,才能正确确定物体的运动性质.2.分析滑块—木板类模型时要抓住一个转折和两个关联
(1)一个转折——滑块与木板达到相同速度或者滑块从木板上滑下是受力和运动状态变化的转折点.
(2)两个关联——转折前、后受力情况之间的关联和滑块、木板位移与板长之间的关联.一般情况下,由于摩擦力或其他力的转变,转折前、后滑块和木板的加速度都会发生变化,因此以转折点为界,对转折前、后进行受力分析是建立模型的关键.典例剖析例4 (18分)如图10所示,传送带Ⅰ与水平面的夹角为30°,传送带Ⅱ与水平面的夹角为37°,两传送带与一小段光滑的水平面BC平滑连接.两传送带均沿顺时针方向匀速率运行.现将装有货物的箱子轻放至传送带Ⅰ的A点,运送到水平面上后,工作人员将箱子内的物体取下,箱子速度不变继续运动到传送带Ⅱ上,传送带Ⅱ的D点与高处平台相切.已知箱子的质量M=1 kg,物体的质量m=3 kg,传送带Ⅰ的速度v1=8 m/s,AB长L1=15 m,与箱子间的动摩擦因数为μ1= .传送带Ⅱ的速度v2=4 m/s,CD长L2=8 m,由于水平面BC上不小心撒上水,致使箱子与传送带Ⅱ间的动摩擦因数变为μ2=0.5,重力加速度g=10 m/s2.求:
(1)装着物体的箱子在传送带Ⅰ上运动的时间;
(2)计算说明,箱子能否运送到高处平台上?
(已知sin 37°=0.6,cos 37°=0.8)图10答案[思维规范流程]μ1(M+m)gcos 30°-(M+m)g·sin 30°2.5 m/s212.8 m3.2 s0.275 s3.475 s答案μ2Mgcos 37°+Mgsin 37°10 m/s22.4 mMgsin 37°>μ2Mgcos 37°答案Mgsin 37°-μ2Mgcos 37°2 m/s24 m不能①⑦?各式2分,其余各式1分8.如图11甲所示,足够长的传送带与水平面夹角为θ,在传送带上某位置轻轻放置一小滑块,小滑块与传送带间动摩擦因数为μ,小滑块速度随时间变化关系如图乙所示,v0、t0已知,则( )解析89√[变式训练]图11√解析 若传送带顺时针转动,当滑块下滑时(mgsin θ>μmgcos θ),将一直匀加速到底端;当滑块上滑时(mgsin θ<μmgcos θ),先匀加速运动,在速度相等后将匀速运动,两种均不符合运动图象;故传送带是逆时针转动,选项A正确.传送带的速度等于v0,选项C错误.89解析答案9.正方形木板水平放置在地面上,木板的中心静置一小滑块(可视为质点),如图12所示为俯视图,为将木板从滑块下抽出,需要对木板施加一个作用线通过木板中心点的水平恒力F.已知木板边长L=2 m、质量M=3 kg,滑块质量m=2 kg,滑块与木板、木板与地面间的动摩擦因数均为μ=0.2,g取10 m/s2,设最大静摩擦力等于滑动摩擦力.求:
(1)要将木板抽出,水平恒力F需满足的条件;图1289解析 能抽出木板,滑块与木板发生相对滑动,当滑块达到随木板运动的最大加速度时,拉力最小.
对滑块,有:μmg=ma
对木板,有:Fmin-μ(M+m)g-μmg=Ma
联立解得:Fmin=2μ(M+m)g=20 N
故抽出木板,水平恒力F至少为20 N
答案 F≥20 N89(2)当水平恒力F=29 N时,在木板抽出时滑块能获得的最大速率.
解析 要使滑块获得的速度最大,则滑块在木板上相对滑动的距离最大,故应沿木板的对角线方向抽木板.
设此时木板加速度为a1,则有:
F-μ(M+m)g-μmg=Ma1vmax=μgt返回解析答案89
(1)解题思路(2)解题技巧
①紧抓“一图三式”,即过程示意图、时间关系式、速度关系式和位移关系式.
②审题应抓住题目中的关键字眼,充分挖掘题目中的隐含条件,如“刚好”
“恰好”“最多”“至少”等,往往对应一个临界状态,满足相应的临界条件.③若被追赶的物体做匀减速运动,一定要注意追上前该物体是否已停止运动,另外还要注意最后对解的讨论分析.
3.处理刹车类问题的思路
先判断刹车时间t0= ,再进行分析计算.解析答案例1 如图1所示,云南省彝良县发生特大泥石流,一汽车停在小山坡底,司机突然发现在距坡底240 m的山坡处泥石流以8 m/s的初速度、0.4 m/s2的加速度匀加速倾泻而下,假设泥石流到达坡底后速率不变,在水平地面上做匀速直线运动.已知司机的反应时间为1 s,汽车启动后以0.5 m/s2的加速度一直做匀加速直线运动.试分析司机能否安全脱离.图1典例剖析解析 设泥石流到达坡底的时间为t1,速度为v1,
v1=v0+a1t1
解得:t1=20 s,v1=16 m/s
而汽车在t2=19 s的时间内发生的位移为:
速度为:v2=a2t2=9.5 m/s
假设再经时间t3,泥石流能够追上汽车,则有:因Δ<0,方程无解,所以泥石流无法追上汽车,司机能安全脱离.
答案 司机能安全脱离1.“蛟龙号”是我国首台自主研制的作业型深海载人潜水器,它是目前世界上下潜能力最强的潜水器.假设某次海试活动中,“蛟龙号”完成海底任务后竖直上浮,从上浮速度为v时开始计时,此后“蛟龙号”匀减速上浮,经过时间t上浮到海面,速度恰好减为零,则“蛟龙号”在t0(t0
(2)看图象:识别两个相关量的变化趋势,从而分析具体的物理过程.
(3)看纵坐标、“斜率”和“面积”:v-t图象中根据坐标值、“斜率”和“面积”可分析速度、加速度和位移的大小、方向特点.x-t图象中根据坐标值、“斜率”可分析位移、速度的大小、方向特点.
(4)看交点:明确图线与图线的交点、图线与坐标轴的交点的物理意义.
(5)一注意:利用v-t图象分析两个物体的运动时,要注意两个物体的出发点,即注意它们是从同一位置出发,还是从不同位置出发.若从不同位置出发,要注意出发时两者的距离.例2 甲、乙两物体从同一地点同时开始沿同一方向运动,甲物体运动的v-t图象为两段直线,乙物体运动的v-t图象为两段半径相同的 圆弧曲线,如图3所示,图中t4=2t2,则在0~t4时间内,以下说法正确的是( )
A.甲物体的加速度不变
B.乙物体做曲线运动
C.两物体t1时刻相距最远,t4时刻相遇
D.甲物体的平均速度等于乙物体的平均速度解析典例剖析图3√解析 0~t2时间段内,甲做匀加速直线运动,t2~t4时间内甲物体做匀减速直线运动,故A错;
速度是矢量,在速度时间图象中,只能表示直线运动,B错;
在整个运动过程中,t3时刻两物体相距最远,C错;
在速度时间图象中,图线下面所包围的面积即为位移,可求知0~t4时间段内,位移相等,故平均速度相同,D对.3.如图4所示,x-t图象反映了甲、乙两车在同一条直线上行驶的位移随时间变化的关系,已知乙车做匀变速直线运动,其图线与t轴相切于10 s处,下列说法正确的是( )
A.5 s时两车速度相等
B.甲车的速度为4 m/s
C.乙车的加速度大小为1.6 m/s2
D.乙车的初位置在x0=80 m处解析34√[变式训练]图4√√解析 位移-时间图象的斜率等于速度,斜率大小越大,速度大小越大,则知5 s时乙车速度较大,故A错误.344.静止在光滑水平面上的物体,同时受到在同一直线
上的力F1、F2作用,F1、F2随时间变化的图象如图5
所示,则物体在0~2t时间内( )
A.离出发点越来越远
B.速度先变大后变小
C.速度先变小后变大
D.加速度先变大后变小
解析 由图线可知,物体受到的合力先减小后增大,加速度先减小后增大,速度一直变大,物体离出发点越来越远,选项A正确.√解析返回34图5 考题三 牛顿运动定律的应用方法指导1.动力学的两类基本问题
(1)由因推果——已知物体的受力情况,确定物体的运动情况.
(2)由果溯因——已知物体的运动情况,确定物体的受力情况.
桥梁:牛顿第二定律F=ma2.超重和失重现象的判断技巧
(1)从受力的角度判断:当物体所受向上的拉力(或支持力)大于重力时,物体处于超重状态,小于重力时处于失重状态,等于零时处于完全失重状态.
(2)从加速度的角度判断:当物体具有向上的加速度时处于超重状态,具有向下的加速度时处于失重状态,向下的加速度为重力加速度时处于完全失重状态.
(3)从速度变化的角度判断:物体向上加速或向下减速时,超重;物体向下加速或向上减速时,失重.3.瞬时性问题的处理
(1)牛顿第二定律是力的瞬时作用规律,加速度和力同时产生、同时变化、同时消失,分析物体在某一时刻的瞬时加速度,关键是分析该瞬时前后的受力情况及其变化.
(2)明确两种基本模型的特点:
①轻绳的形变可瞬时产生或恢复,故绳的弹力可以瞬时突变.
②轻弹簧(或橡皮绳)两端均连有物体时,形变恢复需较长时间,其弹力的大小与方向均不能突变.4.整体法和隔离法的优点及使用条件
(1)整体法:
①优点:研究对象减少,忽略物体之间的相互作用力,方程数减少,求解简捷.
②条件:连接体中各物体具有共同的加速度
(2)隔离法:
①优点:易看清各个物体具体的受力情况.
②条件:当系统内各物体的加速度不同时,一般采用隔离法;求连接体内各物体间的相互作用力时必须用隔离法.典例剖析例3 (2016·四川理综·10)避险车道是避免恶性交通事故的重要设施,由制动坡床和防撞设施等组成,如图6竖直平面内,制动坡床视为与水平面夹角为θ的斜面.一辆长12 m的载有货物的货车因刹车失灵从干道驶入制动坡床,当车速为23 m/s时,车尾位于制动坡床的底端,货物开始在车厢内向车头滑动,当货物在车厢内滑动了4 m时,车头距制动坡床顶端38 m,再过一段时间,货车停止.已知货车质量是货物质量的4倍,货物与车厢间的动摩擦因数为0.4;货车在制动坡床上运动受到的坡床阻力大小为货车和货物总重的0.44倍.货物与货车可分别视为小滑块和
平板,取cos θ=1,sin θ=0.1,g=10 m/s2.
求:图6(1)货物在车厢内滑动时加速度的大小和方向;
解析 设货物的质量为m,货物在车厢内滑动
过程中,货物与车厢的动摩擦因数μ=0.4,
受摩擦力大小为f,加速度大小为a1,则
f+mgsin θ=ma1 ①
f=μmgcos θ ②
联立①②并代入数据得a1=5 m/s2 ③
a1的方向沿制动坡床向下.
答案 5 m/s2 方向沿制动坡床向下解析答案(2)制动坡床的长度.解析答案解析 设货车的质量为M,车尾位于制动坡床底端时的车速为v=23 m/s.货物在车厢内开始滑动到车头距制动坡床顶端s0=38 m的过程中,用时为t,货物相对制动坡床的运动距离为s1,在车厢内滑动的距离s=4 m,货车的加速度大小为a2,货车相对制动坡床的运动距离为s2.货车受到制动坡床的阻力大小为F,F是货车和货物总重的k倍,k=0.44,货车长度l0=12 m,制动坡床的长度为l,则
Mgsin θ+F-f=Ma2 ④
F=k(m+M)g ⑤
⑥解析答案 ⑦
s=s1-s2 ⑧
l=l0+s0+s2 ⑨
联立①~⑨并代入数据得
l=98 m
答案 98 m5.为了让乘客乘车更为舒适,某探究小组设计了一种新的交通工具,乘客的座椅能随着坡度的变化而自动调整,使座椅始终保持水平,如图7所示,当此车加速上坡时,盘腿坐在座椅上的一位乘客( )
A.处于失重状态
B.不受摩擦力的作用
C.受到向前(水平向右)的摩擦力作用
D.所受力的合力竖直向上解析56√[变式训练]7图7解析 车加速上坡,车里的乘客与车相对静止,应该和车具有相同的加速度,方向沿斜坡向上,对乘客受力分析可知,乘客应受到竖直向下的重力,垂直水平面竖直向上的弹力和水平向右的摩擦力,三力合力沿斜面向上,B、D错误,C正确;
弹力大于重力,乘客处于超重状态,A错误.5676.如图8所示,A、B两小球分别连在弹簧两端,B端用绳子固定在倾角为30°的光滑斜面上,若不计弹簧质量,在绳子被剪断瞬间,A、B两球的加速度分别为( )图8解析√567解析 对A:在剪断绳子之前,A处于平衡状态,所以弹簧的拉力等于A的重力沿斜面的分力.在剪断上端的绳子的瞬间,绳子上的拉力立即减为零,而弹簧的伸长量没有来得及发生改变,故弹力不变仍等于A的重力沿斜面的分力.故A球的加速度为零;对B:在剪断绳子之前,对B球进行受力分析,B受到重力、弹簧对它斜向下的拉力、支持力及绳子的拉力,在剪断上端的绳子的瞬间,绳子上的拉力立即减为零,对B球进行受力分析,则B受到重力、弹簧斜向下的拉力、支持力.所以根据牛顿第二定律得5677.如图9所示用力F拉a、b、c三个物体在光滑水平面上运动,现在中间的物体b上加一块橡皮泥,它和中间的物体一起运动,且原拉力F不变,那么加上橡皮泥以后,两段绳的拉力FTa和FTb的变化情况是( )
A.FTa增大 B.FTb增大
C.FTa减小 D.FTb减小567图9解析√√返回567返回 考题四 “传送带”、“滑块-木板模型”问题方法指导1.传送带问题分析的要点是物体与传送带间的摩擦力,关注点是两个时刻:
(1)初始时刻物体相对于传送带的速度或滑动方向决定了该时刻摩擦力的方向.
(2)物体与传送带速度相等的时刻摩擦力的大小(或有无)、性质(滑动摩擦力或静摩擦力)或方向会发生改变.正确判断这两个时刻的摩擦力,才能正确确定物体的运动性质.2.分析滑块—木板类模型时要抓住一个转折和两个关联
(1)一个转折——滑块与木板达到相同速度或者滑块从木板上滑下是受力和运动状态变化的转折点.
(2)两个关联——转折前、后受力情况之间的关联和滑块、木板位移与板长之间的关联.一般情况下,由于摩擦力或其他力的转变,转折前、后滑块和木板的加速度都会发生变化,因此以转折点为界,对转折前、后进行受力分析是建立模型的关键.典例剖析例4 (18分)如图10所示,传送带Ⅰ与水平面的夹角为30°,传送带Ⅱ与水平面的夹角为37°,两传送带与一小段光滑的水平面BC平滑连接.两传送带均沿顺时针方向匀速率运行.现将装有货物的箱子轻放至传送带Ⅰ的A点,运送到水平面上后,工作人员将箱子内的物体取下,箱子速度不变继续运动到传送带Ⅱ上,传送带Ⅱ的D点与高处平台相切.已知箱子的质量M=1 kg,物体的质量m=3 kg,传送带Ⅰ的速度v1=8 m/s,AB长L1=15 m,与箱子间的动摩擦因数为μ1= .传送带Ⅱ的速度v2=4 m/s,CD长L2=8 m,由于水平面BC上不小心撒上水,致使箱子与传送带Ⅱ间的动摩擦因数变为μ2=0.5,重力加速度g=10 m/s2.求:
(1)装着物体的箱子在传送带Ⅰ上运动的时间;
(2)计算说明,箱子能否运送到高处平台上?
(已知sin 37°=0.6,cos 37°=0.8)图10答案[思维规范流程]μ1(M+m)gcos 30°-(M+m)g·sin 30°2.5 m/s212.8 m3.2 s0.275 s3.475 s答案μ2Mgcos 37°+Mgsin 37°10 m/s22.4 mMgsin 37°>μ2Mgcos 37°答案Mgsin 37°-μ2Mgcos 37°2 m/s24 m不能①⑦?各式2分,其余各式1分8.如图11甲所示,足够长的传送带与水平面夹角为θ,在传送带上某位置轻轻放置一小滑块,小滑块与传送带间动摩擦因数为μ,小滑块速度随时间变化关系如图乙所示,v0、t0已知,则( )解析89√[变式训练]图11√解析 若传送带顺时针转动,当滑块下滑时(mgsin θ>μmgcos θ),将一直匀加速到底端;当滑块上滑时(mgsin θ<μmgcos θ),先匀加速运动,在速度相等后将匀速运动,两种均不符合运动图象;故传送带是逆时针转动,选项A正确.传送带的速度等于v0,选项C错误.89解析答案9.正方形木板水平放置在地面上,木板的中心静置一小滑块(可视为质点),如图12所示为俯视图,为将木板从滑块下抽出,需要对木板施加一个作用线通过木板中心点的水平恒力F.已知木板边长L=2 m、质量M=3 kg,滑块质量m=2 kg,滑块与木板、木板与地面间的动摩擦因数均为μ=0.2,g取10 m/s2,设最大静摩擦力等于滑动摩擦力.求:
(1)要将木板抽出,水平恒力F需满足的条件;图1289解析 能抽出木板,滑块与木板发生相对滑动,当滑块达到随木板运动的最大加速度时,拉力最小.
对滑块,有:μmg=ma
对木板,有:Fmin-μ(M+m)g-μmg=Ma
联立解得:Fmin=2μ(M+m)g=20 N
故抽出木板,水平恒力F至少为20 N
答案 F≥20 N89(2)当水平恒力F=29 N时,在木板抽出时滑块能获得的最大速率.
解析 要使滑块获得的速度最大,则滑块在木板上相对滑动的距离最大,故应沿木板的对角线方向抽木板.
设此时木板加速度为a1,则有:
F-μ(M+m)g-μmg=Ma1vmax=μgt返回解析答案89
同课章节目录
