第一节等腰三角形 课时1同步练习

第一节等腰三角形
第1课时 三角形全等与等腰三角形的性质
基础检测
知识点1全等三角形
1.判定两个三角形全等的三个基本事实
为　　　　、　　　　、　　　　;一条判定定理为　　　　　;全等三角形的　　　　、　　　　相等.?
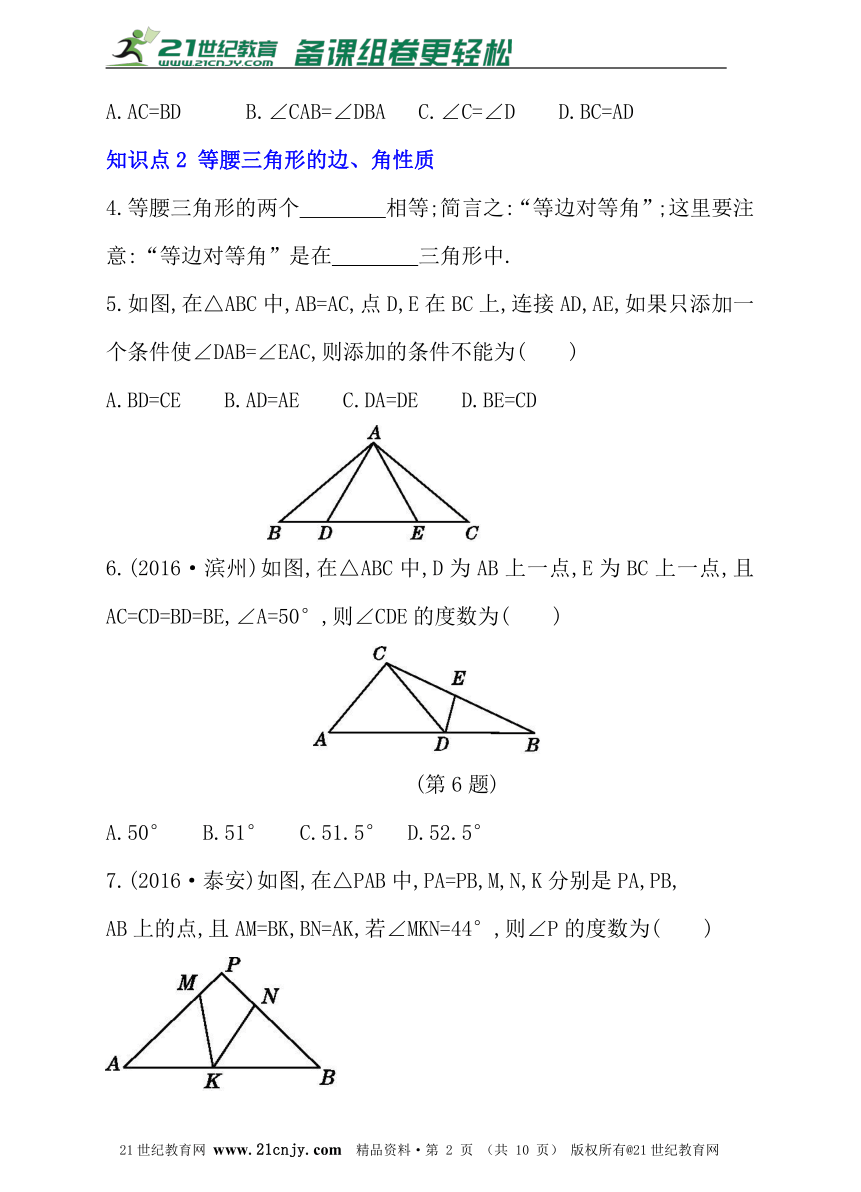
2.(2016·南京)如图,四边形ABCD的对角线AC,BD相交于点O,△ABO≌△ADO.下列结论:2·1·c·n·j·y
①AC⊥BD; ②CB=CD; ③△ABC≌△ADC; ④DA=DC.
其中所有正确结论的序号是　　　　.?
3.(2016·金华)如图,已知∠ABC=∠BAD,添加下列条件还不能判定△ABC≌△BAD的是(　　)【来源：21·世纪·教育·网】

　　　　 　　　　　 　　　　　
A.AC=BD B.∠CAB=∠DBA C.∠C=∠D D.BC=AD
知识点2 等腰三角形的边、角性质
4.等腰三角形的两个　　　　相等;简言之:“等边对等角”;这里要注意:“等边对等角”是在　　　　三角形中.21·世纪*教育网
5.如图,在△ABC中,AB=AC,点D,E在BC上,连接AD,AE,如果只添加一个条件使∠DAB=∠EAC,则添加的条件不能为(　　)2-1-c-n-j-y
A.BD=CE B.AD=AE C.DA=DE D.BE=CD

6.(2016·滨州)如图,在△ABC中,D为AB上一点,E为BC上一点,且AC=CD=BD=BE,∠A=50°,则∠CDE的度数为(　　)21*cnjy*com
(第6题)
A.50° B.51° C.51.5° D.52.5°
7.(2016·泰安)如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,
AB上的点,且AM=BK,BN=AK,若∠MKN=44°,则∠P的度数为(　　)
A.44° 　B.66° C.88° 　D.92°
知识点3 等腰三角形的“三线合一”性质
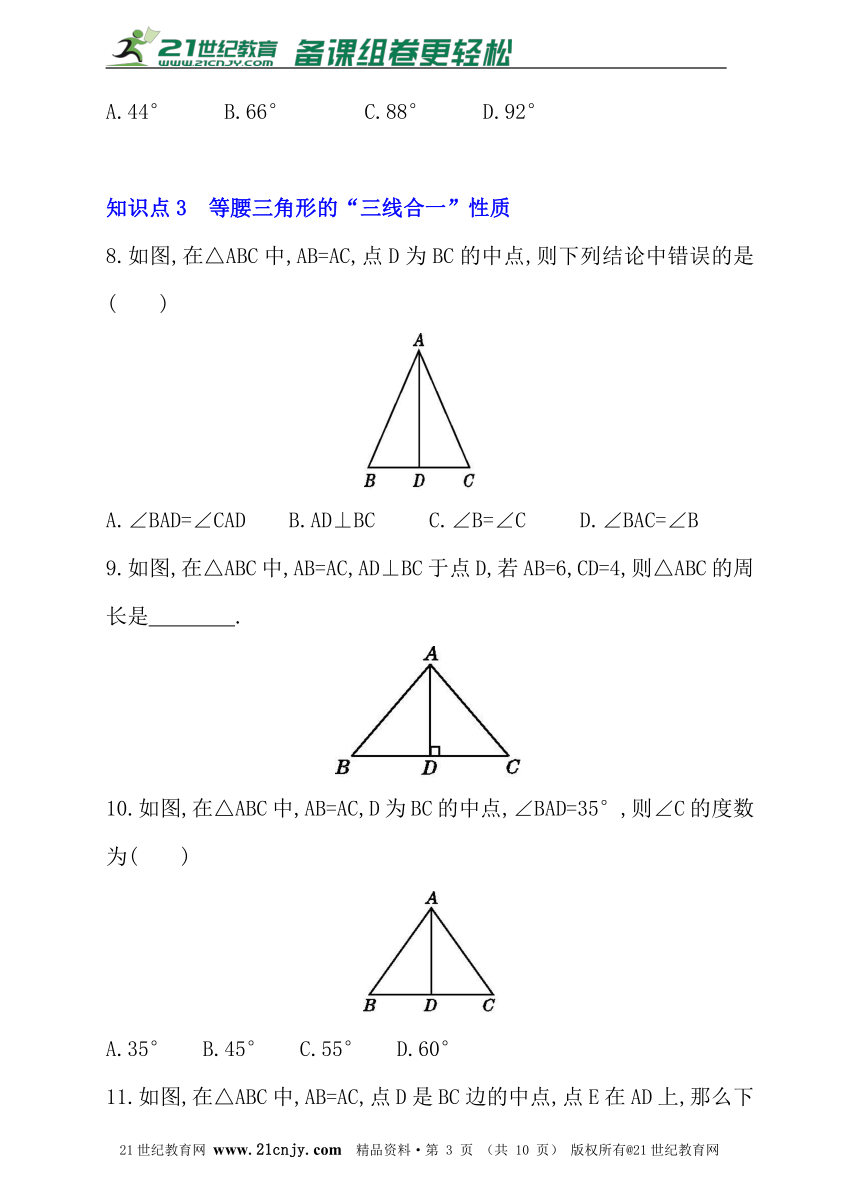
8.如图,在△ABC中,AB=AC,点D为BC的中点,则下列结论中错误的是(　　)

A.∠BAD=∠CAD B.AD⊥BC C.∠B=∠C D.∠BAC=∠B
9.如图,在△ABC中,AB=AC,AD⊥BC于点D,若AB=6,CD=4,则△ABC的周长是　　　　.?21教育网
10.如图,在△ABC中,AB=AC,D为BC的中点,∠BAD=35°,则∠C的度数为(　　)
A.35° B.45° C.55° D.60°
11.如图,在△ABC中,AB=AC,点D是BC边的中点,点E在AD上,那么下列结论不一定正确的是(　　)21cnjy.com
A.AD⊥BC B.∠EBC=∠ECB C.∠ABE=∠ACE D.AE=BE
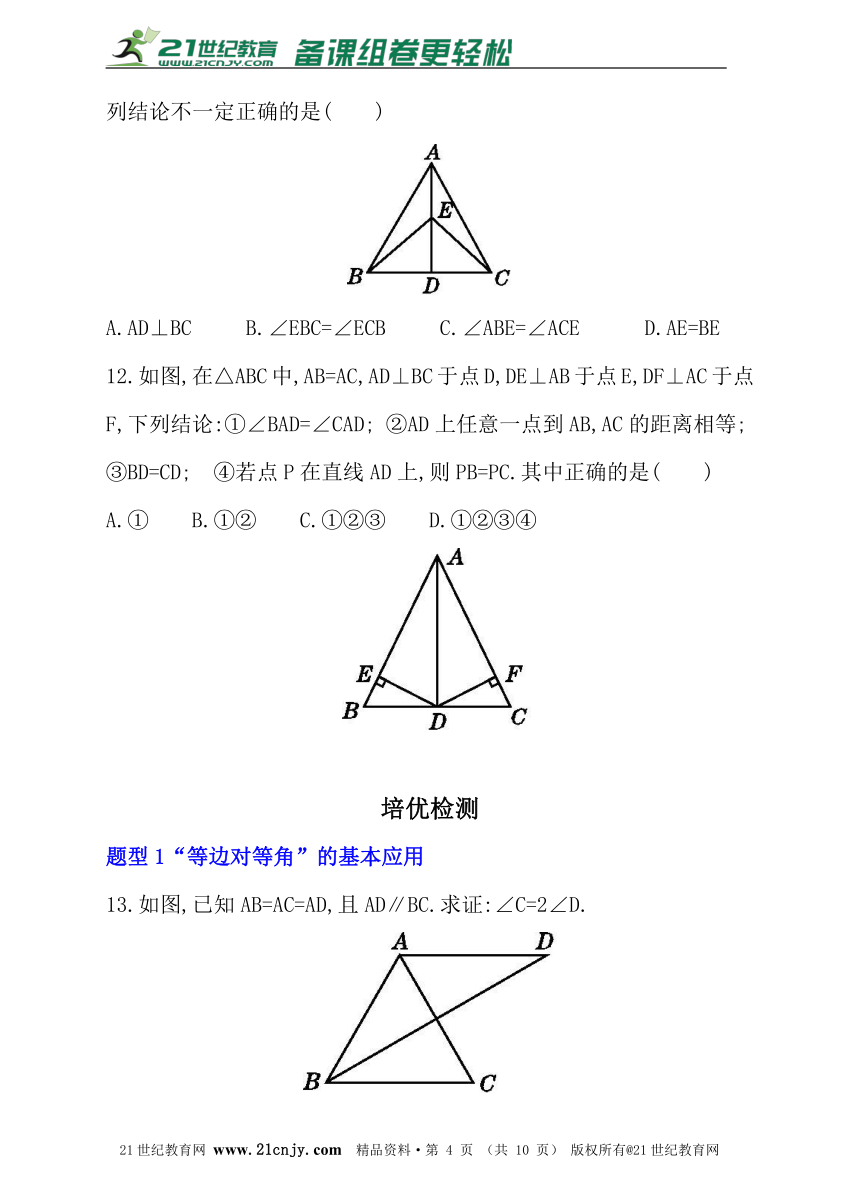
12.如图,在△ABC中,AB=AC,AD⊥BC于点D,DE⊥AB于点E,DF⊥AC于点F,下列结论:①∠BAD=∠CAD; ②AD上任意一点到AB,AC的距离相等;
③BD=CD; ④若点P在直线AD上,则PB=PC.其中正确的是(　　)
①　　B.①②　　C.①②③　　D.①②③④

培优检测
题型1“等边对等角”的基本应用
13.如图,已知AB=AC=AD,且AD∥BC.求证:∠C=2∠D.
题型2“三线合一”的基本应用
14.如图,在△ABC中,AB=AC,AD是BC边上的中线,BE⊥AC于点E.求证:∠CBE=∠BAD.www-2-1-cnjy-com
题型3等腰三角形性质与全等的综合应用
15.如图,在△ABC中,AB=AC,点D是BC边的中点,作∠EAB=∠BAD,AE边交CB的延长线于点E,延长AD到点F,使AF=AE,连接CF.求证:BE=CF.
题型4“三线合一”在证三角形全等中的应用
16.如图①,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.
(1)求证:BE=CE.
(2)如图②,若BE的延长线交AC于点F,且BF⊥AC,垂足为F,AF=BF,原题设其他条件不变.求证:△AEF≌△BCF.【来源：21cnj*y.co*m】
17.如图,AB=AC,∠BAC=90°,∠1=∠2,CE⊥BE.
求证:BD=2CE.
参考答案
1.【答案】.SAS;ASA;SSS;AAS;对应边;对应角
2.【答案】①②③
解:由△ABO≌△ADO得：AB＝AD，∠AOB＝∠AOD＝90°，∠BAC＝∠DAC，又AC＝AC，所以，有△ABC≌△ADC，CB＝CD，所以，①②③正确。
3.【答案】A
解：由题意，得∠ABC=∠BAD，AB=BA，A、∠ABC=∠BAD，AB=BA，AC=BD，（SSA）三角形不全等，故A错误；
4.【答案】底角;同一
5.【答案】C
分析:A、添加BD=CE，可以利用“边角边”证明△ABD和△ACE全等，再根据全等三角形对应角相等得到∠DAB=∠EAC，故本选项错误； B、添加AD=AE，根据等边对等角可得∠ADE=∠AED，然后利用三角形的一个外角等于与它不相邻的两个内角的和求出∠DAB=∠EAC，故本选项错误； C、添加DA=DE无法求出∠DAB=∠EAC，故本选项正确； D、添加BE=CD可以利用“边角边”证明△ABE和△ACD全等，再根据全等三角形对应角相等得到∠DAB=∠EAC，故本选项错误．故选C．
6.【答案】D
解∵AC=CD=BD=BE,∠A=50°,
∴∠A=∠CDA=50°,∠B=∠DCB,∠BDE=∠BED.
∵∠B+∠DCB=∠CDA=50°,∴∠B=25°.
∵∠B+∠EDB+∠DEB=180°,
∴∠BDE=∠BED=×(180°-25°)=77.5°.
∴∠CDE=180°-∠CDA-∠BDE=180°-50°-77.5°=52.5°.
7.【答案】D
解∵PA=PB,∴∠A=∠B.
在△AMK和△BKN中,
∴△AMK≌△BKN.∴∠AMK=∠BKN.
∵∠MKB=∠MKN+∠NKB=∠A+∠AMK,
∴∠A=∠MKN=44°.
∴∠P=∠180°-∠A-∠B=92°.
8.【答案】D
解：∵AB=AC，点D为BC的中点，∴∠BAD=∠CAD，AD⊥BC，∠B=∠C．故A、B、C正确，D错误．故选D．21·cn·jy·com
9.【答案】20
10.【答案】C
解：AB=AC，D为BC中点?∴AD 平分∠BAC，AD⊥BC∴∠DAC=∠BAD=35°，∠ADC=90°∴∠C=∠ADC -∠DAC=55° 故选C
11.【答案】D
解：∵AB=AC，点D是BC边上的中点，∴AD⊥BC，故A选项正确；∴EB=EC，∴∠EBC=∠ECB，故B选项正确；又∵AB=AC，∴∠ABC=∠ACB，∴∠ABC-∠EBC=∠ACB-∠ECB，即∠ABE=∠ACE，故C选项正确；根据题目条件无法得到∠ABE=∠BAE，所以，AE=BE不一定正确，故D选项错误．因为本题选择不正确的，故选：D．www.21-cn-jy.com
12.【答案】D
解：∵AB=AC，∴△ABC是等腰三角形，又∵AD⊥BC于D，∴∠BAD=∠CAD，BD=CD，故①③正确；∵∠BAD=∠CAD，∴AD上任意一点到AB、AC的距离相等，故②正确；∵AD是BC的中垂线，∴若点P在直线AD上，则PB=PC，故④正确．故选D．21世纪教育网版权所有
13.证明:∵AB=AC=AD,
∴∠C=∠ABC,∠D=∠ABD.
∵AD∥BC,
∴∠CBD=∠D.
∴∠ABC=∠ABD+∠CBD=2∠D.
∴∠C=2∠D.
14.证明:∵AB=AC,∴∠ABD=∠C.
又∵AD是BC边上的中线,∴AD⊥BC.
∵BE⊥AC于点E,∴∠BEC=∠ADB=90°.
∴∠C+∠CBE=∠ABD+∠BAD=90°.
∴∠CBE=∠BAD.
15.证明:∵AB=AC,点D是BC的中点,
∴∠BAD=∠CAD.
∵∠EAB=∠BAD,
∴∠EAB=∠CAD.
又∵AE=AF,AB=AC,
∴△ABE≌△ACF(SAS).
∴BE=CF.
16.证明:(1)∵AB=AC,D是BC的中点,∴∠BAE=∠CAE.在△ABE和△ACE中,
∴△ABE≌△ACE(SAS).∴BE=CE.
(2)∵AB=AC,点D是BC的中点,∴AD⊥BC.
∴∠EAF+∠C=90°.
∵BF⊥AC,∴∠CBF+∠C=90°.∴∠EAF=∠CBF.
在△AEF和△BCF中,
∴△AEF≌△BCF(ASA).
证明:延长CE交BA的延长线于点F,如图所示.

∵CE⊥BE,∴∠BEC=∠BEF=90°.
又∵∠1=∠2,∴∠F=∠BCE.∴BC=BF.
∴CE=FE=CF,即CF=2CE.　
∵∠F+∠2=90°,∠F+∠ACF=90°,∴∠2=∠ACF.
又∵AB=AC,∠BAD=∠CAF=90°,
∴△BDA≌△CFA(ASA).
∴BD=CF.∴BD=2CE.