第一节等腰三角形 课时2同步练习

第一节等腰三角形
第2课时 等边三角形的性质
基础检测
知识点1等腰三角形中相等的线段
1.等腰三角形两底角的平分线_______;两腰上的高_______;两腰上的中线_______.
2.在等腰三角形ABC中,AB=AC,那么下列说法中不正确的是(　　)
A.BC边上的高线和中线互相重合
B.AB边上的中线和AC边上的中线相等
C.顶点B处的角平分线和顶点C处的角平分线相等
D.AB,BC边上的高线相等
3.如图,已知在△ABC中,AB=AC,给出下列条件,不能使BD=CE的是(　　)
A.BD和CE分别为AC和AB边上的中线
B.BD和CE分别为∠ABC和∠ACB的平分线
C.BD和CE分别为AC和AB边上的高
D.∠ABD=∠BCE
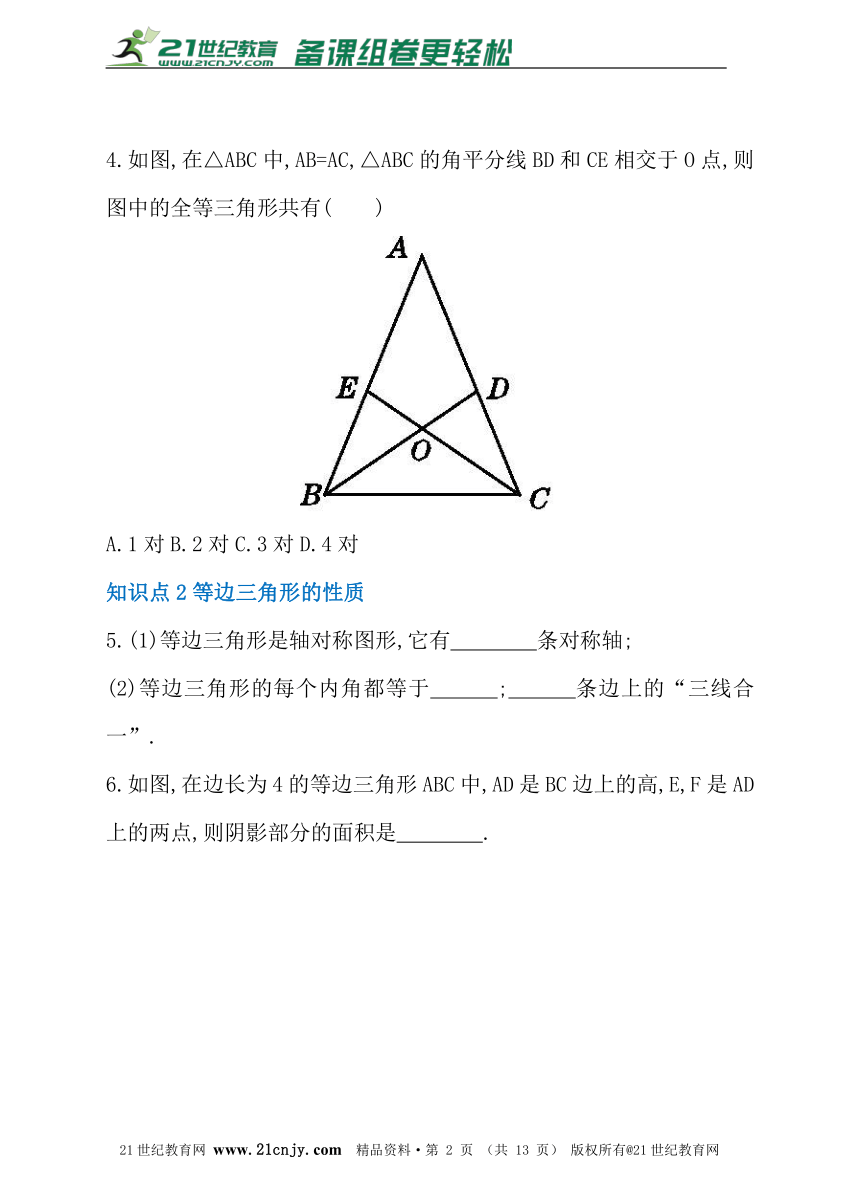
4.如图,在△ABC中,AB=AC,△ABC的角平分线BD和CE相交于O点,则图中的全等三角形共有(　　)
A.1对 B.2对 C.3对 D.4对
知识点2等边三角形的性质
5.(1)等边三角形是轴对称图形,它有　　　　条对称轴;　?
(2)等边三角形的每个内角都等于　　　;　　　条边上的“三线合一”.?
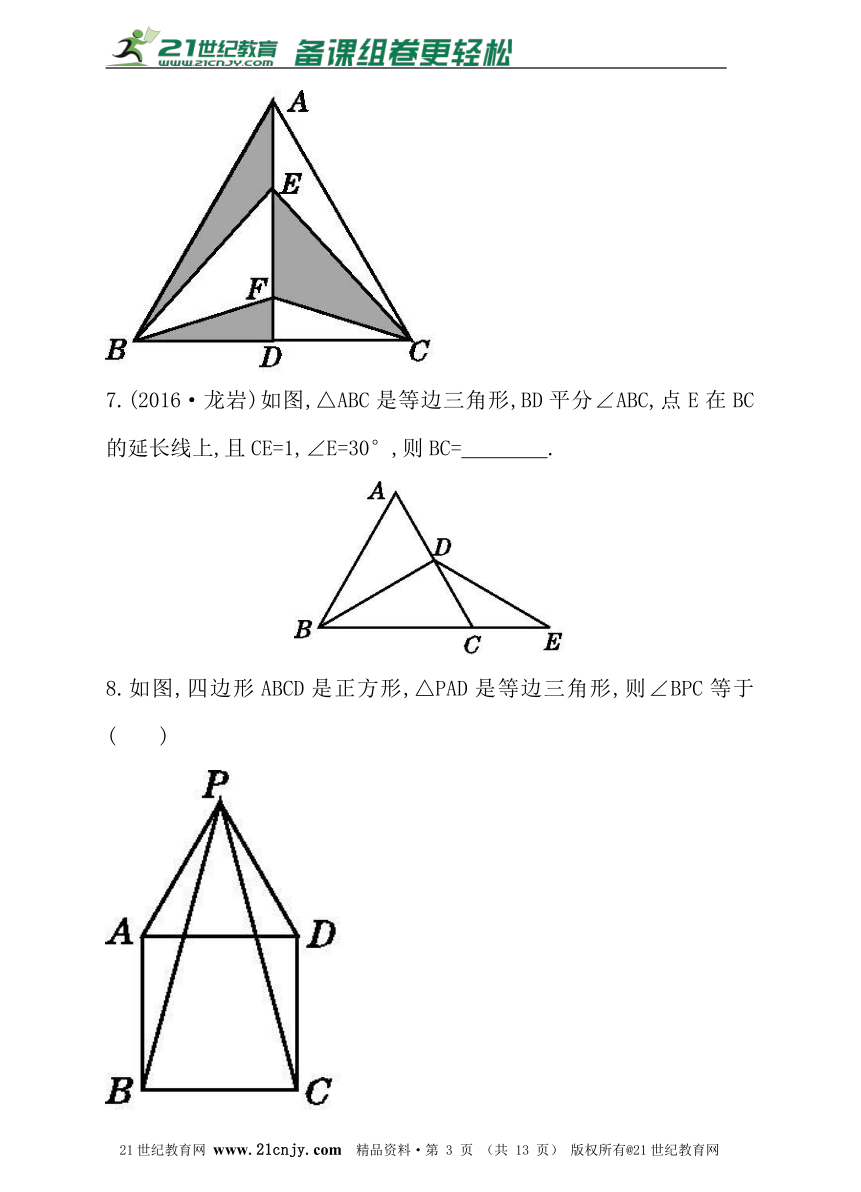
6.如图,在边长为4的等边三角形ABC中,AD是BC边上的高,E,F是AD上的两点,则阴影部分的面积是　　　　.?
7.(2016·龙岩)如图,△ABC是等边三角形,BD平分∠ABC,点E在BC的延长线上,且CE=1,∠E=30°,则BC=　　　　.?
8.如图,四边形ABCD是正方形,△PAD是等边三角形,则∠BPC等于(　　)
A.20° B.30° C.35° D.40°
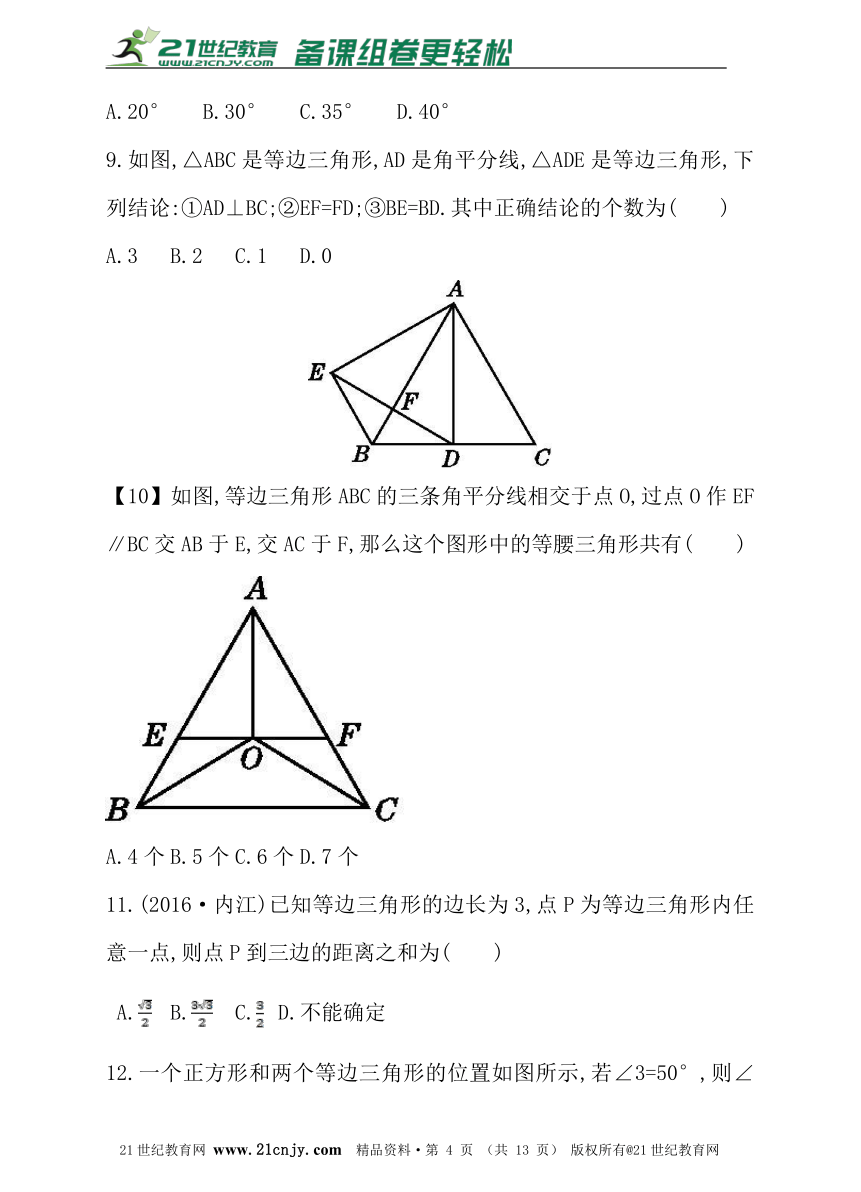
9.如图,△ABC是等边三角形,AD是角平分线,△ADE是等边三角形,下列结论:①AD⊥BC;②EF=FD;③BE=BD.其中正确结论的个数为(　　)
A.3 B.2 C.1 D.0
【10】如图,等边三角形ABC的三条角平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,那么这个图形中的等腰三角形共有(　　)
A.4个 B.5个 C.6个 D.7个
11.(2016·内江)已知等边三角形的边长为3,点P为等边三角形内任意一点,则点P到三边的距离之和为(　　)
A. B. C. D.不能确定
12.一个正方形和两个等边三角形的位置如图所示,若∠3=50°,则∠1+∠2等于(　　)
A.90° B.100° C.130° D.180°
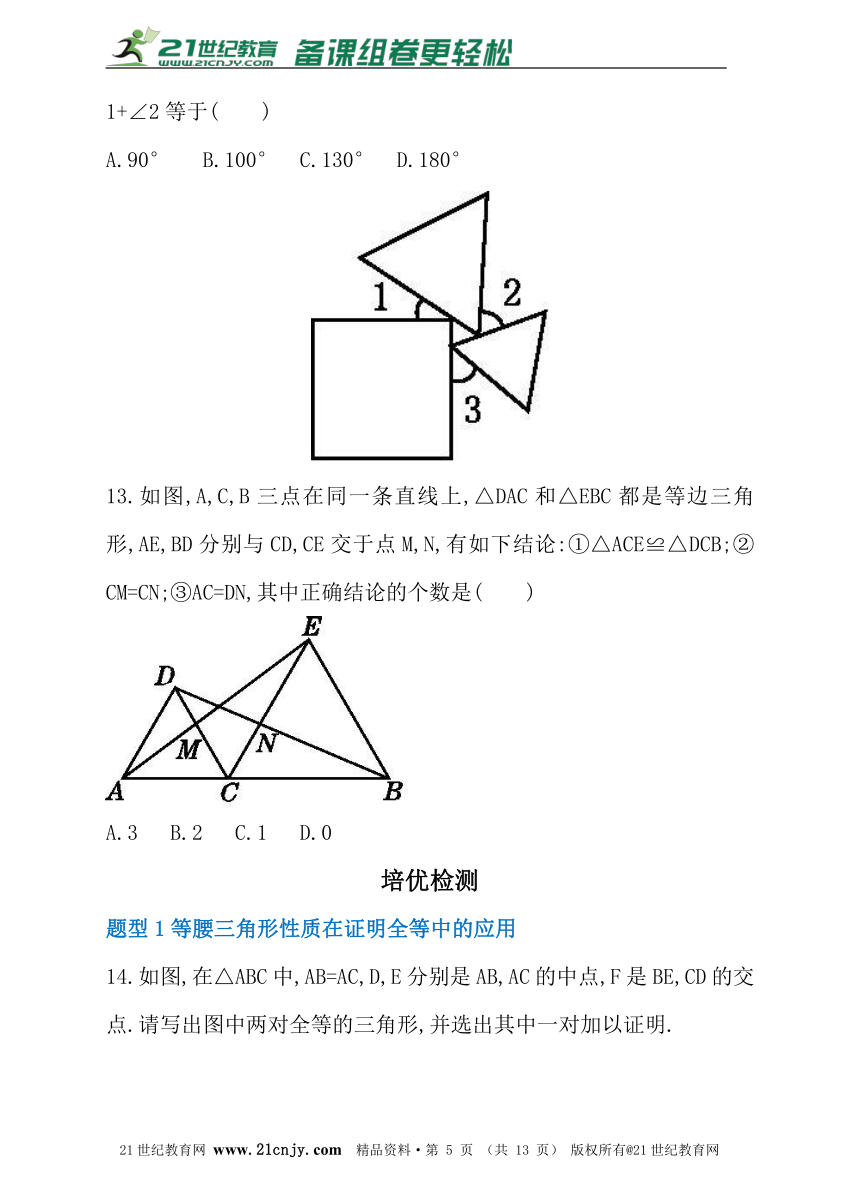
13.如图,A,C,B三点在同一条直线上,△DAC和△EBC都是等边三角形,AE,BD分别与CD,CE交于点M,N,有如下结论:①△ACE≌△DCB;②CM=CN;③AC=DN,其中正确结论的个数是(　　)
A.3 B.2 C.1 D.0
培优检测
题型1等腰三角形性质在证明全等中的应用
14.如图,在△ABC中,AB=AC,D,E分别是AB,AC的中点,F是BE,CD的交点.请写出图中两对全等的三角形,并选出其中一对加以证明.
题型2等边三角形性质在求边、角中的应用
15.如图,在等边三角形ABC中,点D,E分别在边BC,AB上,且BD=AE,AD与CE交于点F.
(1)求证:AD=CE;
(2)求∠DFC的度数.
题型3等边三角形性质在证边相等中的应用
16.如图,B是AC上一点,△ABD和△DCE都是等边三角形.求证:AC=BE.
题型4构造全等三角形法在证明边、角关系中的应用
17.如图,△ABC是等边三角形,D是边BC上(除B,C外)的任意一点,∠ADE=60°,且DE交∠ACF的平分线CE于点E.求证:
(1)∠1=∠2;
(2)AD=DE.
参考答案
1.【答案】相等;相等;相等　
2.【答案】D
解：A、BC边上的高线和中线互相重合，故本选项正确， B、AB和AC边上的中线相等，故本选项正确， C、三角形ABC中∠B和∠C的角平分线相等，所以此题选D
3.【答案】D　
4.【答案】C
解：①△BCE≌△CBD理由：∵AB=AC∴∠B=∠C∵BE=CD，BC=BC∴△BCE≌△CBD；②△BOE≌△COD理由：∵∠EOB=∠DOC，∠EBO=∠DCO，BE=CD∴△BOE≌△COD；③△ABD≌△ACE理由：∵AB=AC，∠A=∠A，∠ABD=∠ACE∴△ABD≌△ACE．故选C．
5.【答案】(1)3　(2)60°;三
6.【答案】2
解：在直角三角形中，两直角的平方和等于斜边的平方在说说你这道题 因为在等腰三角形中（等边也行）底边的高线也是中线,顶角的角平分线,由此可知BD=DC=1/2BC=2再由勾股定理
AD^=AB^-BD^=16-4=12 所以AD=√12=2√3所以S三角形
ABD=1/2BDxAD=1/2x2x2√3=2√3
7.【答案】2
解：∵△ABC是等边三角形，?
∴∠ABC=∠ACB=60°，BA=BC，?
∵BD平分∠ABC，?
∴∠DBC=∠E=30°，BD⊥AC，?
∴?∠BDC=90°，?∴BC=2DC，?
∵∠ACB=∠E+∠CDE，?
∴∠CDE=∠E=30°，?
∴CD=CE=1，?∴BC=2CD=2，?故答案为2?
8.【答案】B
∵四边形ABCD是正方形，△PAD是等边三角形，
∴∠BAP=∠BAD+∠PAB=90°+60°=150°．∵PA=AD，AB=AD，∴PA=AB，∴∠ABP=
180°-150°
2
=15°，
∴∠PBC=∠ABC-∠ABP=90°-15°=75°，
同理：∠PCB=75°，∴∠BPC=180°-75°-75°=30°．故答案为30°．
9.【答案】A
∵△ABC是等边三角形，∴AB=AC，∵AD是∠BAC的平分线，∴AD⊥BC，BD=DC，∴∠ADC=90°，∵△ABC和△ADE是等边三角形，∴AE=AD，AB=AC，∠EAD=∠BAC=60°，∴∠EAD-∠BAD=∠BAC-∠BAD，∴∠BAE=∠DAC，在△BAE和△CAD中，
AE＝AD
∠EAB∠DAC
AB＝AC
∴△BAE≌△CAD（SAS），∴∠DAC=∠BAE，BE=DC，∵BD=DC，∴BE=BD，∵△ABC是等边三角形，∴∠BAC=60°，∵AD是∠BAC的平分线，∴∠DAC=30°，∴∠BAE=30°，∵△ADE是等边三角形，∴∠DAE=60°，∴∠BAD=30°=∠BAE，∵AE=AD，∴EF=DF（三线合一），即①②③都正确，故选A．
10.【答案】D
解：根据角平分线的性质和等边三角形的性质就可以求出角相等，利用角相等根据等腰三角形的判定定理究竟可以求出图中的等腰三角形的个数，从而得出答案．
解：∵△ABC是等边三角形，
∴∠ABC=∠ACB=∠BAC
∵等边△ABC的三条角平分线相交于点O，
∴∠1=∠2=∠3=∠4=∠7=∠8=30°，
∵EF∥BC，
∴∠4=∠5=30°，∠7=∠8=30°，∠9=∠ABC=60°，∠10=∠ACB=60°．
∴∠9=∠10，∠3=∠5，∠6=∠7．∴△BEO，△CFO，△BOC，△AOB，△AOC，△AEF，△ABC是等腰三角形，共有7个．故选D．
11.【答案】B
12.【答案】B　
解:如图,由题意可知∠ABC+∠ACB=∠3+60°=110°,∠ABC=90°-∠1,∠ACB=120°-∠2,则90°-∠1+120°-∠2=110°,解得∠1+∠2=100°.
13.【答案】B
解：解：∵△DAC和△EBC都是等边三角形∴AC=CD，CE=BC，∠ACD=∠ECB=60°∴∠ACE=∠DCB∴△ACE≌△DCB（SAS）（①正确）∴∠AEC=∠DBC∵∠DCE+∠ACD+∠ECB=180°，∠ACD=∠ECB=60°∴∠DCE=∠ECB=60°∵CE=BC，∠DCE=∠ECB=60°，∠AEC=∠DBC∴△EMC≌△BNC（ASA）∴CM=CN（②正确）∵AC=DC 在△DNC中，DC所对的角为∠DNC=∠NCB+∠NBC=60°+∠NBC＞60°，而DN所对的角为60°，根据三角形中等边对等角、大边对大角，小边对小角的规律，则DC＞DN，即是AC＞DN，所以③错误，所以正确的结论有两个．故选B．
14.解:△ABE≌△ACD,△DBC≌△ECB或△BFD≌△CFE(写出两个即可).
选证△ABE≌△ACD(其他两对证明略).
证明:∵D,E分别是AB,AC的中点,
∴AD=AB,AE=AC.
又∵AB=AC,∴AD=AE.
在△ABE和△ACD中,
∴△ABE≌△ACD(SAS).
15.(1)证明:∵△ABC是等边三角形,
∴∠BAC=∠B=60°,AB=AC.
又∵AE=BD,
∴△AEC≌△BDA(SAS).
∴AD=CE.
(2)解:由(1)知△AEC≌△BDA,
∴∠ACE=∠BAD.
∴∠DFC=∠FAC+∠ACE=∠FAC+∠BAD=∠BAC=60°.　
16.证明:∵△ABD和△DCE都是等边三角形,
∴∠ADB=∠CDE=60°,AD=BD,CD=DE.
∴∠ADB+∠BDC=∠BDC+∠FDE,即∠ADC=∠BDE,
∴△ADC≌△BDE.
∴AC=BE.
17.证明:(1)∵△ABC是等边三角形,∠ADE=60°,
∴∠ADE=∠B=60°.
又∵∠ADC=∠2+∠ADE=∠1+∠B,∴∠1=∠2.
(2)如图,在AB上取一点M,使BM=BD,连接MD.
∵△ABC是等边三角形,∴∠B=60°.
∴△BMD是等边三角形,∠BMD=60°,∠AMD=120°.
∵CE是∠ACF的平分线,
∴∠ECA=60°,∠DCE=120°.
∴∠AMD=∠DCE.
∵BA-BM=BC-BD,
∴MA=CD.
在△AMD和△DCE中,
∴△AMD≌△DCE(ASA).
∴AD=DE.