第一节等腰三角形 课时3同步练习

第一节等腰三角形
第3课时 等腰三角形的判定
基础检测
知识点1等腰三角形的判定
1.如果一个三角形有两个角相等,那么这两个角所对的边也_____;简称:“等角对_____”.?
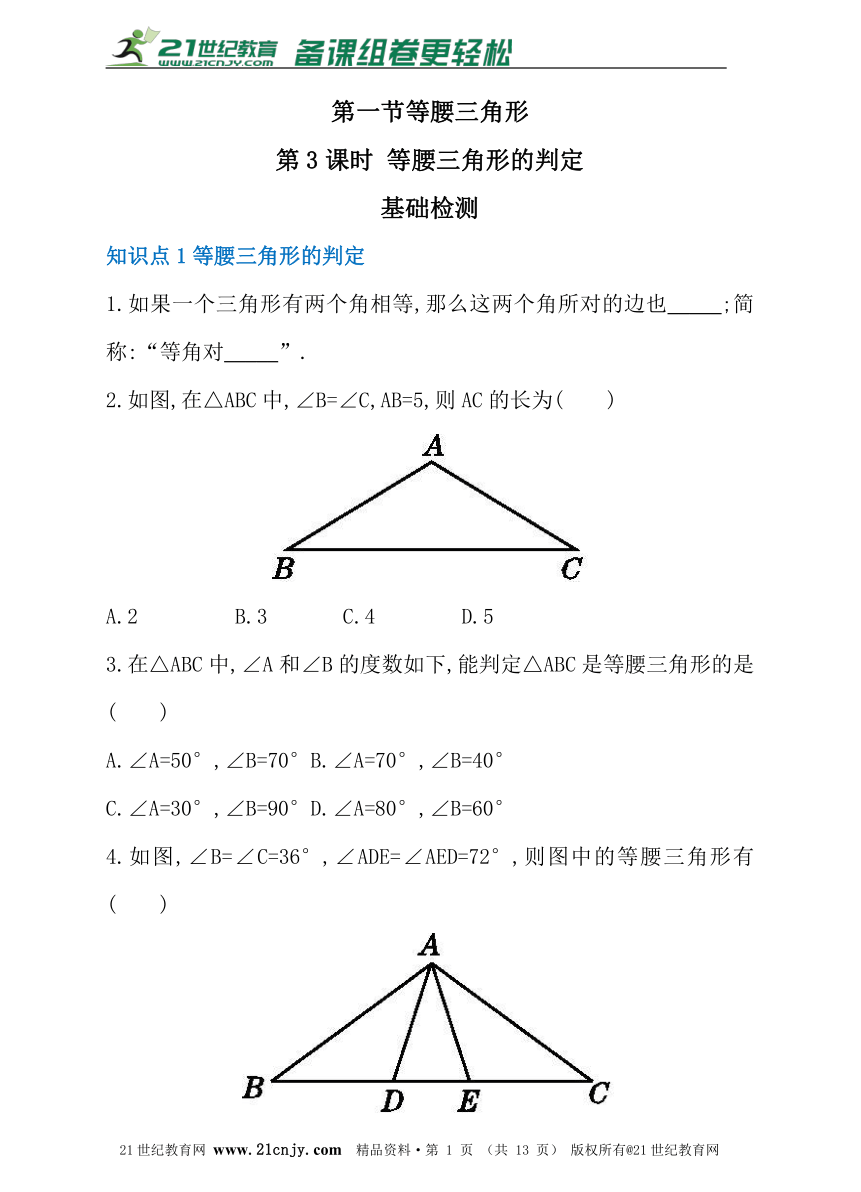
2.如图,在△ABC中,∠B=∠C,AB=5,则AC的长为(　　)
A.2 　　　B.3 C.4 　　　D.5
3.在△ABC中,∠A和∠B的度数如下,能判定△ABC是等腰三角形的是(　　)
A.∠A=50°,∠B=70°B.∠A=70°,∠B=40°
C.∠A=30°,∠B=90°D.∠A=80°,∠B=60°
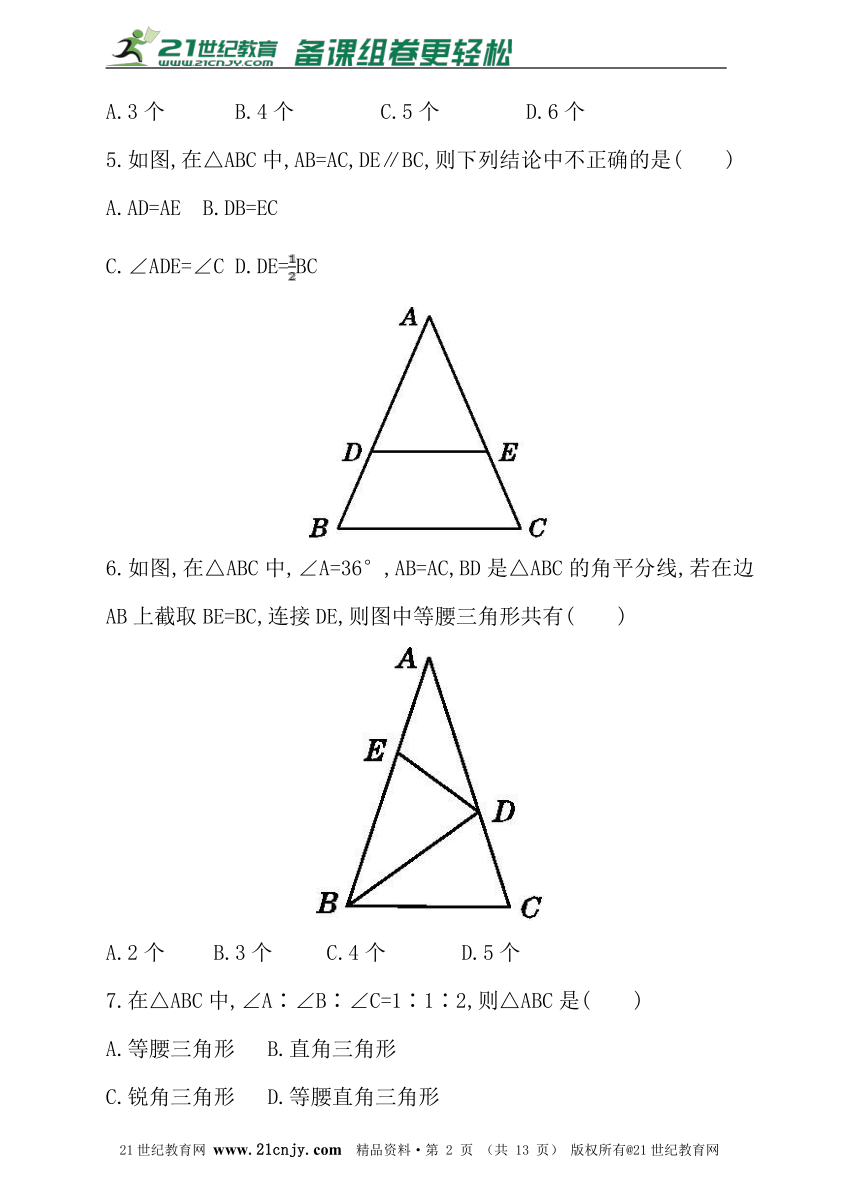
4.如图,∠B=∠C=36°,∠ADE=∠AED=72°,则图中的等腰三角形有(　　)
A.3个 　　　B.4个 C.5个 　　　D.6个
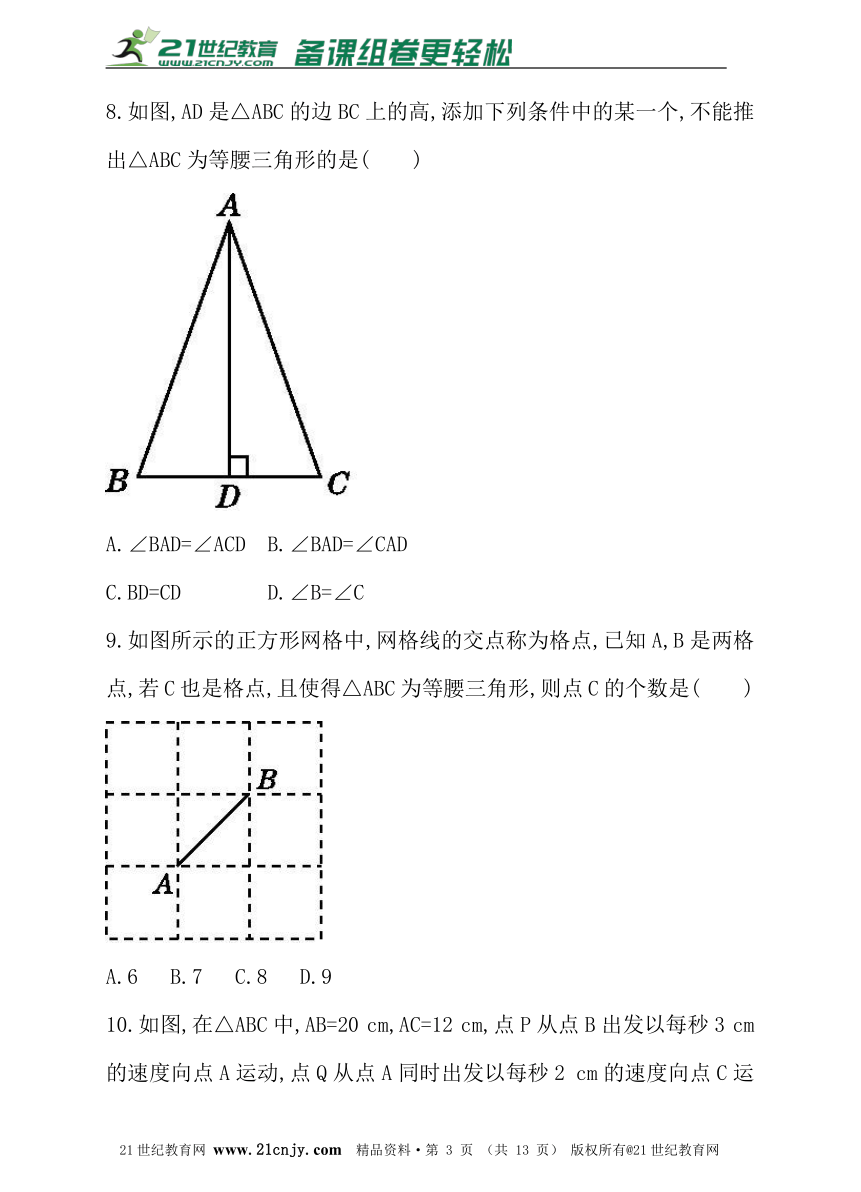
5.如图,在△ABC中,AB=AC,DE∥BC,则下列结论中不正确的是(　　)
A.AD=AE B.DB=EC
C.∠ADE=∠C D.DE=BC
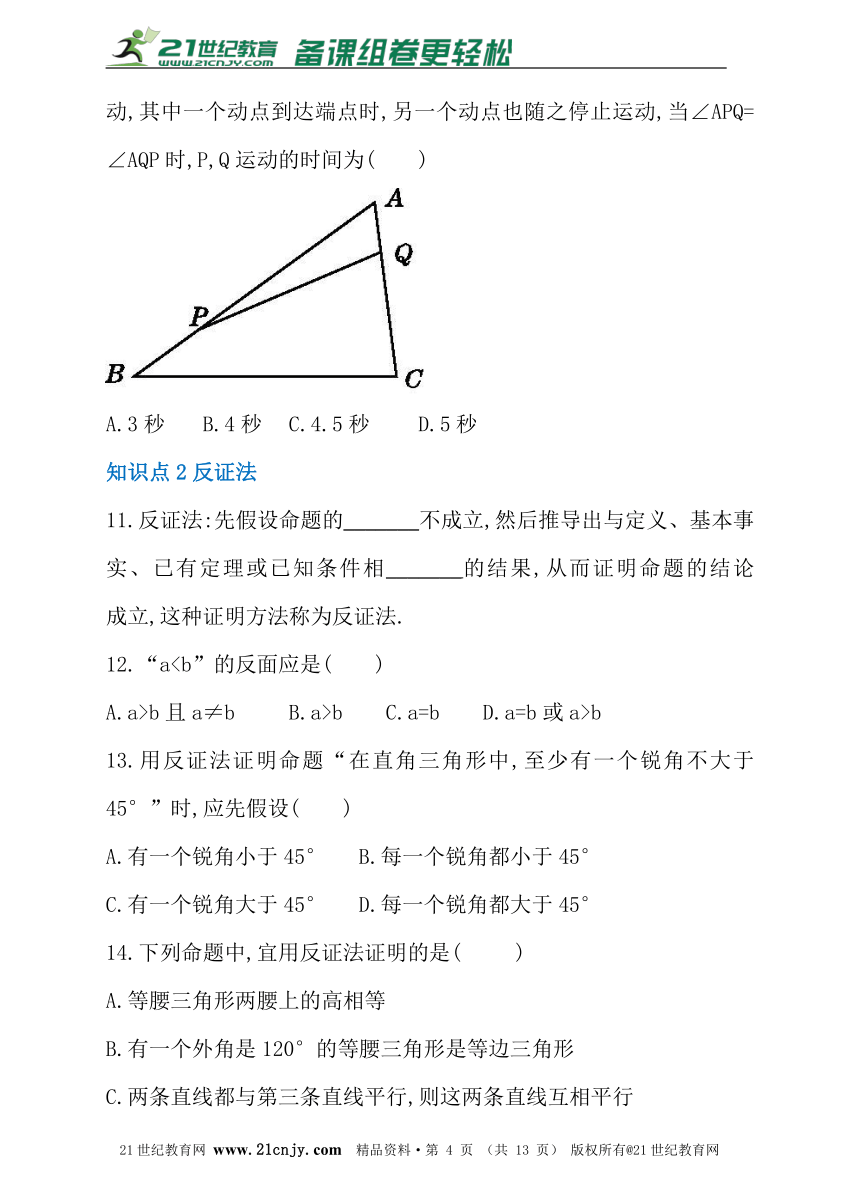
6.如图,在△ABC中,∠A=36°,AB=AC,BD是△ABC的角平分线,若在边AB上截取BE=BC,连接DE,则图中等腰三角形共有(　　)
A.2个 B.3个 C.4个 D.5个
7.在△ABC中,∠A∶∠B∶∠C=1∶1∶2,则△ABC是(　　)
A.等腰三角形 B.直角三角形
C.锐角三角形 D.等腰直角三角形
8.如图,AD是△ABC的边BC上的高,添加下列条件中的某一个,不能推出△ABC为等腰三角形的是(　　)
A.∠BAD=∠ACD B.∠BAD=∠CAD
C.BD=CD D.∠B=∠C
9.如图所示的正方形网格中,网格线的交点称为格点,已知A,B是两格点,若C也是格点,且使得△ABC为等腰三角形,则点C的个数是(　　)
A.6 B.7 C.8 D.9
10.如图,在△ABC中,AB=20 cm,AC=12 cm,点P从点B出发以每秒3 cm的速度向点A运动,点Q从点A同时出发以每秒2 cm的速度向点C运动,其中一个动点到达端点时,另一个动点也随之停止运动,当∠APQ=∠AQP时,P,Q运动的时间为(　　)
A.3秒 B.4秒 C.4.5秒 D.5秒
知识点2反证法
11.反证法:先假设命题的_______不成立,然后推导出与定义、基本事实、已有定理或已知条件相_______的结果,从而证明命题的结论　　　　成立,这种证明方法称为反证法.
12.“aA.a>b且a≠b B.a>b C.a=b D.a=b或a>b
13.用反证法证明命题“在直角三角形中,至少有一个锐角不大于45°”时,应先假设(　　)
A.有一个锐角小于45° B.每一个锐角都小于45°
C.有一个锐角大于45° D.每一个锐角都大于45°
14.下列命题中,宜用反证法证明的是(　 　)
A.等腰三角形两腰上的高相等
B.有一个外角是120°的等腰三角形是等边三角形
C.两条直线都与第三条直线平行,则这两条直线互相平行
D.全等三角形的面积相等
培优检测
题型1等角对等边在证等腰三角形中的应用
15.如图,在△ABC中,AB=AC,D是AB上的一点,过点D作DE⊥BC于E,并与CA的延长线交于点F.
求证:△ADF是等腰三角形.
题型2等腰三角形的判定在折叠中的应用
16.把一张长方形纸条按如图方式折叠,BD为折痕,重合部分是什么形状?请说明理由.
题型3等腰三角形判定和性质的综合应用
17.如图,在△ABC中,AB=AC,D为BC边的中点,F为CA的延长线上的一点,过点F 作FG⊥BC于G点,并交AB于E点.求证:
(1)AD∥FG;
(2)△AFE为等腰三角形.
题型4等腰三角形判定和性质在构造全等三角形中的应用
18.如图,在△ABC中,AB=AC,EF交AB于点E,交AC的延长线于点F,交BC于点D,且BE=CF.
求证:DE=DF.
参考答案
1.【答案】相等;等边
2.【答案】D
解：∵∠B=∠C，AB=5，∴AB=AC=5。故选D。
3.【答案】B
解；当顶角为∠A=50°时，∠B=65°，当顶角为∠B=70°时，∠A=55°所以A选项错误．当顶角为∠B=40°时，∠A=70°，所以B选项正确．当顶角为∠A=30°时，∠B=75°，当顶角为∠B=90°时，∠A=45°所以C选项错误．当顶角为∠A=80°时，∠B=50°，当顶角为∠B=60°时，∠A=60°所以D选项错误．故选B．
4.【答案】D
解：∵∠B=∠C=36°，∠ADE=∠AED=72°，∴△ABC和△ADE是等腰三角形，∵∠B=36°，∠ADE=72°，∴∠BAD=36°，∴AD=BD，∴△ABD是等腰三角形，同理△AEC是等腰三角形，∵∠ADE=∠AED=72°，∴∠DAE=36°，∴∠CAD=36°+36°=72°，∴∠CAD=∠CDA=72°，∴△ADC是等腰三角形，同理：△ABE是等腰三角形，综上所述：等腰三角形有6个，故选：D．
5.【答案】D
解：解：∵DE∥BC，
∴=，∠ADE=∠B，
∵AB=AC，
∴AD=AE，DB=EC，∠B=∠C，
∴∠ADE=∠C，
而DE不一定等于BC，
故选D．
6.【答案】D
解：∵AB=AC，
∴△ABC是等腰三角形；
∵AB=AC，∠A=36°，
∴∠ABC=∠C=72°，
∵BD是△ABC的角平分线，
∴∠ABD=∠DBC=∠ABC=36°，
∴∠A=∠ABD=36°，
∴BD=AD，
∴△ABD是等腰三角形；
在△BCD中，∵∠BDC=180°﹣∠DBC﹣∠C=180°﹣36°﹣72°=72°，
∴∠C=∠BDC=72°，
∴BD=BC，
∴△BCD是等腰三角形；
∵BE=BC，
∴BD=BE，
∴△BDE是等腰三角形；
∴∠BED=（180°﹣36°）÷2=72°，
∴∠ADE=∠BED﹣∠A=72°﹣36°=36°，
∴∠A=∠ADE，
∴DE=AE，
∴△ADE是等腰三角形；
∴图中的等腰三角形有5个．
故选D．
7.【答案】D
解：设一份为k°，则三个内角的度数分别为k°，k°，2k°．则k°+k°+2k°=180°，解得k°=45°．∴2k°=90°，所以这个三角形是等腰直角三角形．故选D
8.【答案】A
9.【答案】C
解：如吓图：分情况讨论．
①AB为等腰△ABC底边时，符合条件的C点有4个；②AB为等腰△ABC其中的一条腰时，符合条件的C点有4个．故选：C．
10.【答案】B
设运动的时间为x,在△ABC中,AB=20cm,AC=12cm,点P从点B出发以每秒3cm的速度向点A运动,点Q从点A同时出发以每秒2cm的速度向点C运动,当△APQ是等腰三角形时,AP=AQ,（当PA=PQ和QA=QP时,无法求出x的值）AP=20-3x,AQ=2x即20-3x=2x,解得x=4．故选B
11.【答案】结论;矛盾;一定
12.【答案】D
13.【答案】D
解：反证法的第一步是假设命题的结论不成立，据此可以得到答案．
若用反证法证明命题“在直角三角形中，至少有一个锐角不大于45°”时，应假设每一个角都小于45°．故选D。
14.【答案】C
A、利用三角形的面积公式比较容易证明，故选项错误；B、利用等边三角形的判定定理即可直接证明，故选项错误；C、正确；D、根据全等的定义可以直接证明，故选项错误．故选C．
15.证明:∵DE⊥BC于E,
∴∠F+∠C=90°,∠B+∠BDE=90°.
∵∠FDA=∠BDE,
∴∠B+∠FDA=90°.
∴∠F+∠C=∠B+∠FDA.
而AB=AC,∴∠B=∠C.
∴∠F=∠FDA.
∴AF=AD,即△ADF是等腰三角形.
16.解:重合部分△BDE是等腰三角形.理由如下:
∵△BC'D是由△BCD翻折得到的,
∴△BC'D与△BCD关于直线BD成轴对称.
∴∠EBD=∠CBD.
又∵四边形ABCD是长方形,
∴AD∥BC.
∴∠EDB=∠CBD.
∴∠EDB=∠EBD.
∴BE=DE,即△BDE是等腰三角形.
点拨:解决此题运用了轴对称的性质及“等角对等边”,注意折叠前后的图形全等.
17.证明:(1)∵AB=AC,D是BC的中点,
∴AD⊥BC.
又∵FG⊥BC,∴AD∥FG.
(2)∵AB=AC,D是BC的中点,∴∠BAD=∠CAD.
∵AD∥FG,∴∠F=∠CAD,∠AEF=∠BAD.
∴∠F=∠AEF.
∴AF=AE,即△AEF是等腰三角形.
18.证明:过点E作EG∥AC,交BC于点G,
∴∠F=∠DEG,∠ACB=∠EGB.
∵AB=AC,∴∠ACB=∠B(等边对等角).
∴∠B=∠EGB.
∴BE=EG(等角对等边).
∵BE=CF,∴EG=CF.
在△EGD和△FCD中,
∴△EGD≌△FCD(AAS).
∴DE=DF.