第一节等腰三角形 课时4同步练习

第一节等腰三角形
第4课时 等边三角形的判定
基础检测
知识点1等边三角形的判定
1.三个角都　　　　的三角形是等边三角形;有一个角是　　　　的等腰三角形是等边三角形.?
2.等腰三角形补充下列条件后,仍不一定成为等边三角形的是(　　)
A.有一个内角是60° B.有一个外角是120°
C.有两个角相等 D.腰与底边相等
3.下列三角形:
①有两个角等于60°的三角形;
②有一个角等于60°的等腰三角形;
③三个外角(每个顶点处各取一个外角)都相等的三角形;
④一腰上的中线也是这条腰上的高的等腰三角形.
其中是等边三角形的有(　　)
A.①②③　B.①②④　C.①③　D.①②③④
4.如图,木工师傅从边长为90 cm的正三角形木板上锯出一个正六边形木板,那么正六边形木板的边长为(　　)21·cn·jy·com
A.34 cm　　B.32 cm　　C.30 cm　　D.28 cm
5.(2015·荆门)如图,点A,B,C在一条直线上,△ABD,△BCE均为等边三角形,连接AE和CD,AE分别交CD,BD于点M,P,CD交BE于点Q,连接PQ,BM,下面的结论:①△ABE≌△DBC;②∠DMA=60°;③△BPQ为等边三角形;④MB平分∠AMC,其中结论正确的有(　　) www.21-cn-jy.com
A.1个 B.2个 C.3个 D.4个
6.(2016·河北)如图,∠AOB=120°,OP平分∠AOB,且OP=2.若点M,N分别在OA,OB上,且△PMN为等边三角形,则满足上述条件的△PMN有(　　)2·1·c·n·j·y
A.1个
B.2个
C.3个
D.3个以上
知识点2含30°角的直角三角形的性质
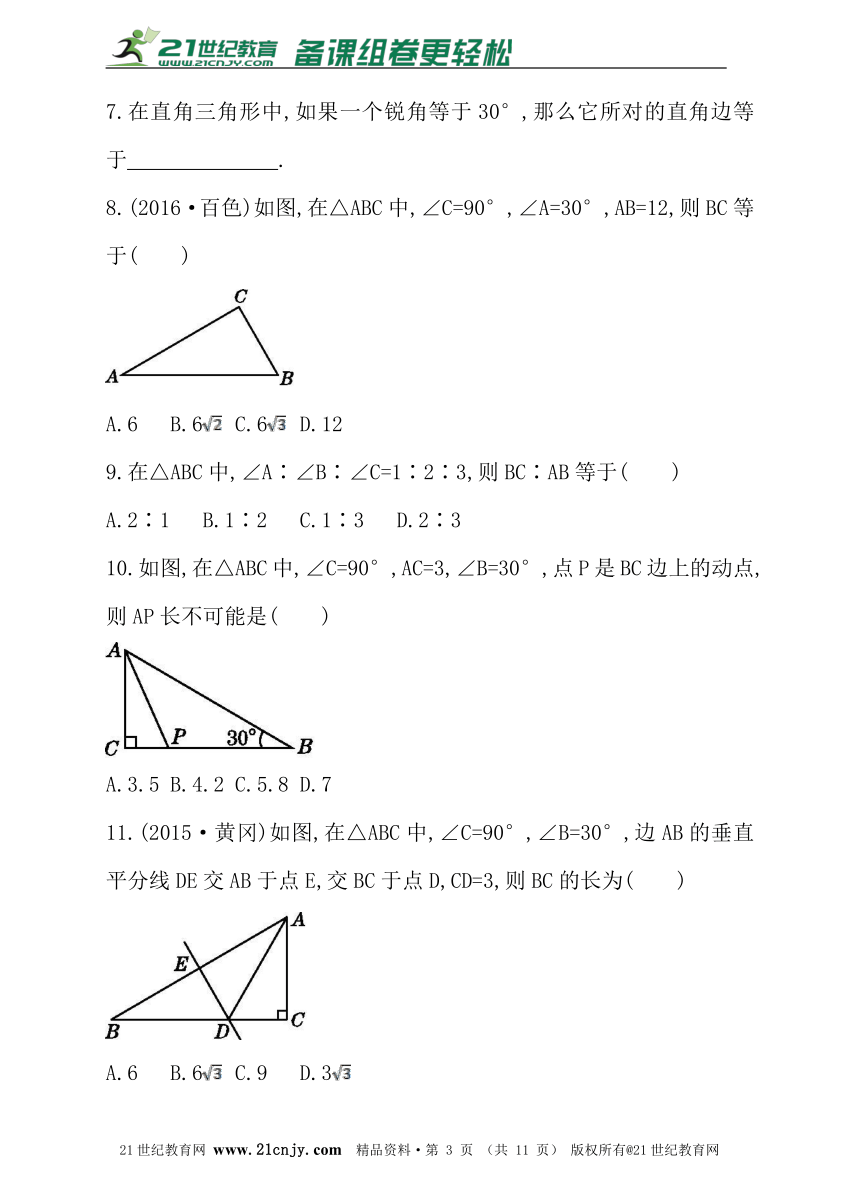
7.在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于　　　　　　　.?
8.(2016·百色)如图,在△ABC中,∠C=90°,∠A=30°,AB=12,则BC等于(　　)21世纪教育网版权所有
A.6 B.6 C.6 D.12
9.在△ABC中,∠A∶∠B∶∠C=1∶2∶3,则BC∶AB等于(　　)
A.2∶1 B.1∶2 C.1∶3 D.2∶3
10.如图,在△ABC中,∠C=90°,AC=3,∠B=30°,点P是BC边上的动点,则AP长不可能是(　　)www-2-1-cnjy-com
A.3.5 B.4.2 C.5.8 D.7
11.(2015·黄冈)如图,在△ABC中,∠C=90°,∠B=30°,边AB的垂直平分线DE交AB于点E,交BC于点D,CD=3,则BC的长为(　　)
A.6 B.6 C.9 D.3
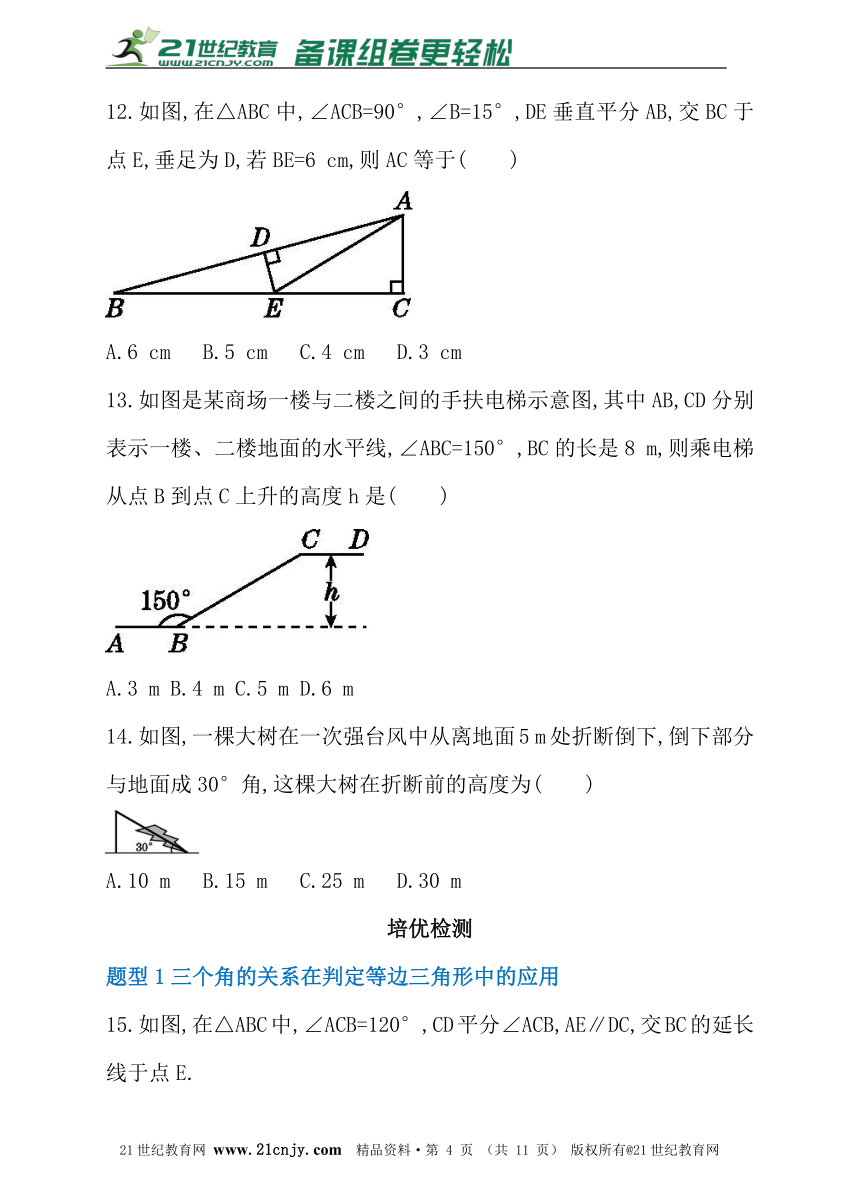
12.如图,在△ABC中,∠ACB=90°,∠B=15°,DE垂直平分AB,交BC于点E,垂足为D,若BE=6 cm,则AC等于(　　)【来源：21cnj*y.co*m】
A.6 cm B.5 cm C.4 cm D.3 cm
13.如图是某商场一楼与二楼之间的手扶电梯示意图,其中AB,CD分别表示一楼、二楼地面的水平线,∠ABC=150°,BC的长是8 m,则乘电梯从点B到点C上升的高度h是(　　)【版权所有：21教育】
A.3 m B.4 m C.5 m D.6 m
14.如图,一棵大树在一次强台风中从离地面5 m处折断倒下,倒下部分与地面成30°角,这棵大树在折断前的高度为(　　)
A.10 m B.15 m C.25 m D.30 m
培优检测
题型1三个角的关系在判定等边三角形中的应用
15.如图,在△ABC中,∠ACB=120°,CD平分∠ACB,AE∥DC,交BC的延长线于点E.
求证:△ACE是等边三角形.
题型2三边关系在判定等边三角形中的应用
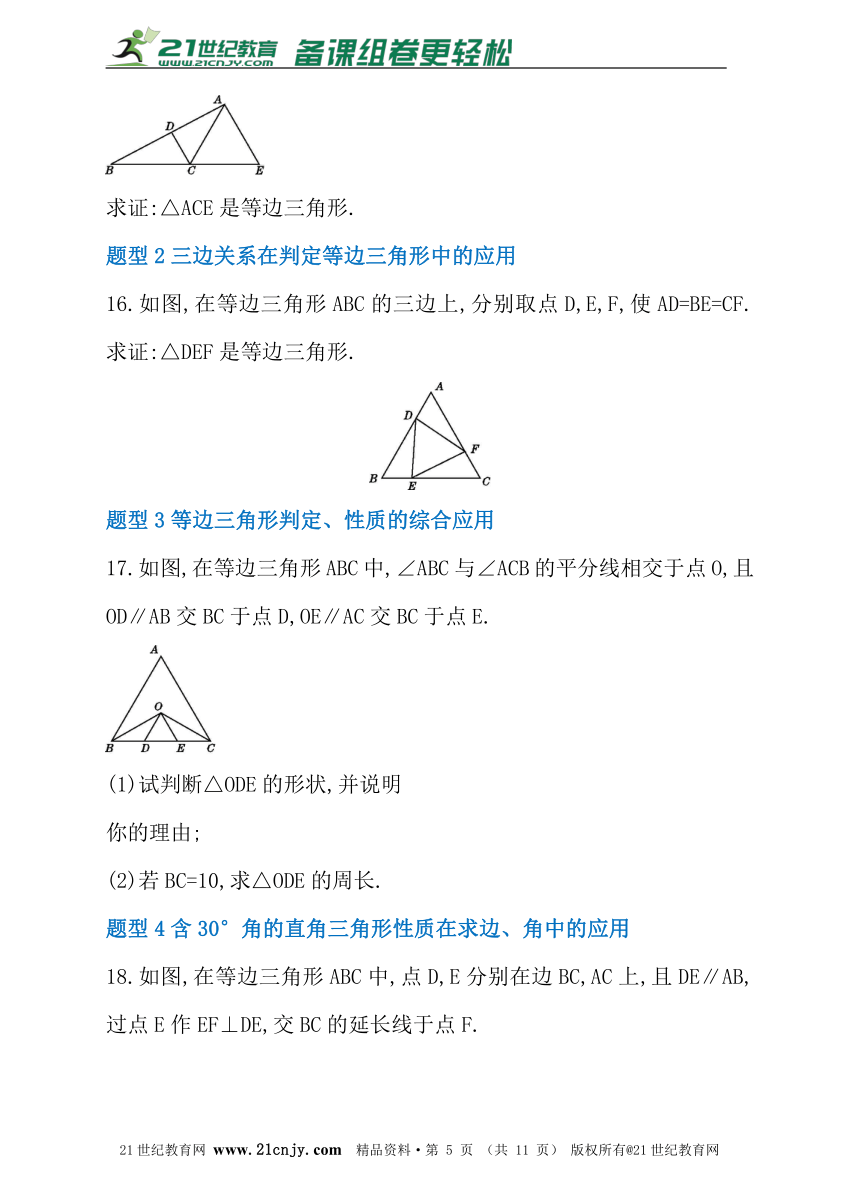
16.如图,在等边三角形ABC的三边上,分别取点D,E,F,使AD=BE=CF.求证:△DEF是等边三角形.21*cnjy*com
题型3等边三角形判定、性质的综合应用
17.如图,在等边三角形ABC中,∠ABC与∠ACB的平分线相交于点O,且OD∥AB交BC于点D,OE∥AC交BC于点E.21*cnjy*com
(1)试判断△ODE的形状,并说明
你的理由;
(2)若BC=10,求△ODE的周长.
题型4含30°角的直角三角形性质在求边、角中的应用
18.如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.21cnjy.com
(1)求∠F的度数;
(2)若CD=2,求DF的长.
参考答案
1.【答案】相等;60°　
2.【答案】C
解：A、有一个角是60°的等腰三角形是等边三角形，故本选项正确；B、有一个外角是120°，则该等腰三角形的一个内角是60°，根据“有一个角是60°的等腰三角形是等边三角形”推知，有一外角为120°的等腰三角形是等边三角形；故本选项正确；C、有两个角相等的等腰三角形有可能还是等腰三角形；故本选项错误；D、腰与底边相等的等腰三角形的三条边相等，所以腰与底边相等的等腰三角形是等边三角形；故本选项正确；故选C．【来源：21·世纪·教育·网】
3.【答案】D
解：根据等边三角形的性质和定义，可得：有一个角为60°的等腰三角形是等边三角形；三个内角都相等的三角形为等边三角形；三边相等的三角形是等边三角形；再由中线、高的性质和三角形内角和定理，依次分析各项即可判断。①两个角为60度，则第三个角也是60度，则其是等边三角形，故正确；②这是等边三角形的判定2，故正确；③三个外角相等则三个内角相等，则其是等边三角形，故正确；④根据等边三角形三线合一性质，故正确．所以都正确．故选D．
4.【答案】C
解：图中小三角形也是正三角形，且边长等于正六边形的边长，所以正六边形的周长是正三角形的周长的2/3，正六边形的周长为90×3×（2/3）=180cm，所以正六边形的边长是180÷6=30cm．故选C．
5.【答案】D
解：解：∵△ABD、△BCE为等边三角形，∴AB=DB，∠ABD=∠CBE=60°，BE=BC，∴∠ABE=∠DBC，∠PBQ=60°，在△ABE和△DBC中，
21·世纪*教育网
AB=DB ∠ABE=∠DBC BE=BC
∴△ABE≌△DBC（SAS），
∴①正确；∵△ABE≌△DBC，∴∠BAE=∠BDC，∵∠BDC+∠BCD=180°-60°-60°=60°，∴∠DMA=∠BAE+∠BCD=∠BDC+∠BCD=60°，∴②正确；在△ABP和△DBQ中，
∠BAP=∠BDQ AB=DB ∠ABP=∠DBQ=0°
∴△ABP≌△DBQ（ASA），∴BP=BQ，∴△BPQ为等边三角形，∴③正确；∵∠DMA=60°，∴∠AMC=120°，∴∠AMC+∠PBQ=180°，∴P、B、Q、M四点共圆，∵BP=BQ，∴
∴∠BMP=∠BMQ，即MB平分∠AMC；∴④正确；综上所述：正确的结论有4个；故选：D．
6.【答案】D　
解:如图,在OA,OB上截取OE=OF=OP,作∠MPN=60°.
∵OP平分∠AOB,
∴∠EOP=∠POF=60°.
∵OP=OE=OF,
∴△OPE,△OPF是等边三角形.
∴EP=OP,∠EPO=∠OEP=∠PON=∠MPN=60°,
∴∠EPM=∠OPN.
在△PEM和△PON中,
∴△PEM≌△PON(ASA).
∴PM=PN.又∵∠MPN=60°,
∴△PMN是等边三角形,
∴只要∠MPN=60°,△PMN就是等边三角形.
故这样的三角形有无数个.
7.【答案】斜边的一半　
8.【答案】A
解：∵在△ABC中，∠A=30°，∠C=90°，∴BC=1/2=AB，∵AB=12，∴BC=6，故选A．21教育网
9.【答案】B
解：因为∠A :∠B :∠C = 1:2:3所以∠B = 2∠A,∠C = 3∠A又因为 ∠A + ∠B + ∠C = 180o所以 ∠A + 2∠A + 3∠A = 180o所以 ∠A = 30o所以 ∠C = 90o所以BC：AB = 1:2?
2-1-c-n-j-y
10.【答案】D
解：利用垂线段最短分析AP最小不能小于3；利用含30度角的直角三角形的性质得出AB=6，可知AP最大不能大于6。故选D。
11.【答案】C
解：解：∵DE是AB的垂直平分线，
∴AD=BD，
∴∠DAE=∠B=30°，
∴∠ADC=60°，
∴∠CAD=30°，
∴AD为∠BAC的角平分线，
∵∠C=90°，DE⊥AB，
∴DE=CD=3，
∵∠B=30°，
∴BD=2DE=6，
∴BC=9，
故选C．
12.【答案】D
13.【答案】B
解：
过C作CM⊥AB于M则CM=h，∠CMB=90°，∵∠ABC=150°，∴∠CBM=30°，∴h=CM=1/2,BC=4m，故选B．【出处：21教育名师】
14.【答案】B
解：如图，在Rt△ABC中，∠C=90°，CB=5，∠A=30°∴AB=10，∴大树的高度为10+5=15m．故选B．21教育名师原创作品
15.证明:∵CD平分∠ACB,∴∠BCD=∠ACD.
∵AE∥DC,∴∠CAE=∠ACD,∠E=∠BCD.
∴∠CAE=∠E.
∵∠ACB=120°,∴∠ACE=60°.
∴∠CAE=∠E=∠ACE=60°.
∴△ACE为等边三角形.
16.证明:∵△ABC是等边三角形,
∴∠A=∠B=∠C=60°,AB=BC=CA.
∵AD=BE=CF,∴BD=CE=AF.
∴△BDE≌△CEF≌△AFD(SAS).
∴DE=EF=FD.
∴△DEF是等边三角形.
方法总结:证明一个三角形是等边三角形的三种方法:(1)证三条边相等;(2)证三个角相等;(3)证等腰三角形中有一个角等于60°.
17.解:(1)△ODE是等边三角形.理由如下:
∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°.
∵OD∥AB,OE∥AC,
∴∠ODE=∠ABC=60°,∠OED=∠ACB=60°.
∴∠DOE=60°.
∴∠DOE=∠ODE=∠OED.
∴△ODE是等边三角形.
(2)∵BO平分∠ABC,且∠ABC=60°,
∴∠OBD=30°.
∴∠BOD=∠ODE-∠OBD=60°-30°=30°.
∴∠OBD=∠BOD.
∴BD=OD.
同理可得:CE=OE.
∴△ODE的周长=OD+DE+OE=BD+DE+CE=BC=10.
18.解:(1)∵△ABC是等边三角形,∴∠B=60°.
∵DE∥AB,∴∠EDC=∠B=60°.
∵EF⊥DE,∴∠DEF=90°.
∴∠F=90°-∠EDC=30°.
(2)∵∠ACB=60°,∠EDC=60°,
∴∠DEC=60°.
∴△EDC是等边三角形.
∴DE=DC=2.
∵∠DEF=90°,∠F=30°,∴DF=2DE=4.