第二节 直角三角形 课时1同步练习
图片预览
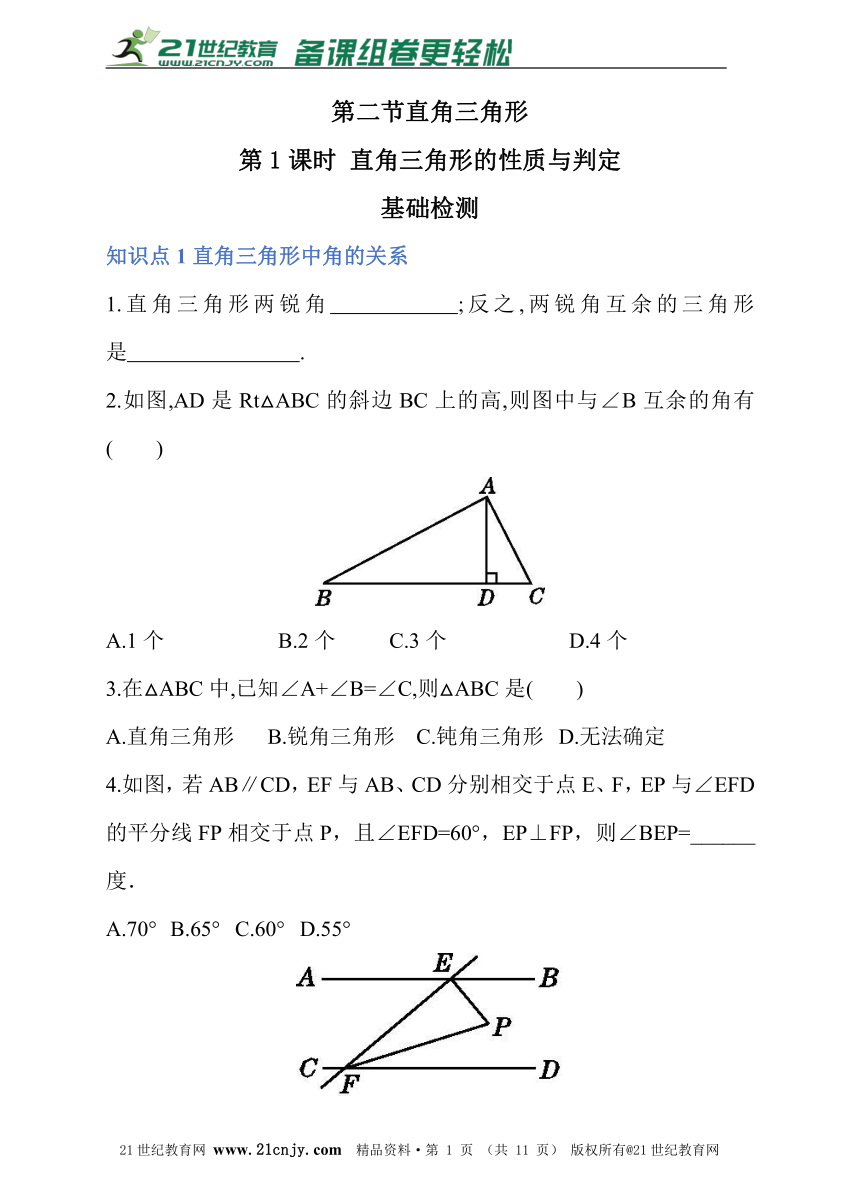


文档简介
第二节直角三角形
第1课时 直角三角形的性质与判定
基础检测
知识点1直角三角形中角的关系
1.直角三角形两锐角 ;反之,两锐角互余的三角形是 .?
2.如图,AD是Rt△ABC的斜边BC上的高,则图中与∠B互余的角有( )
A.1个 B.2个 C.3个 D.4个
3.在△ABC中,已知∠A+∠B=∠C,则△ABC是( )
A.直角三角形 B.锐角三角形 C.钝角三角形 D.无法确定
4.如图,若AB∥CD,EF与AB、CD分别相交于点E、F,EP与∠EFD的平分线FP相交于点P,且∠EFD=60°,EP⊥FP,则∠BEP=______度.21教育网
A.70° B.65° C.60° D.55°
5.(2016·咸宁)如图,直线l1∥l2,CD⊥AB于点D,∠1=50°,则∠BCD的度数为( )21cnjy.com
A.50° B.45° C.40° D.30°
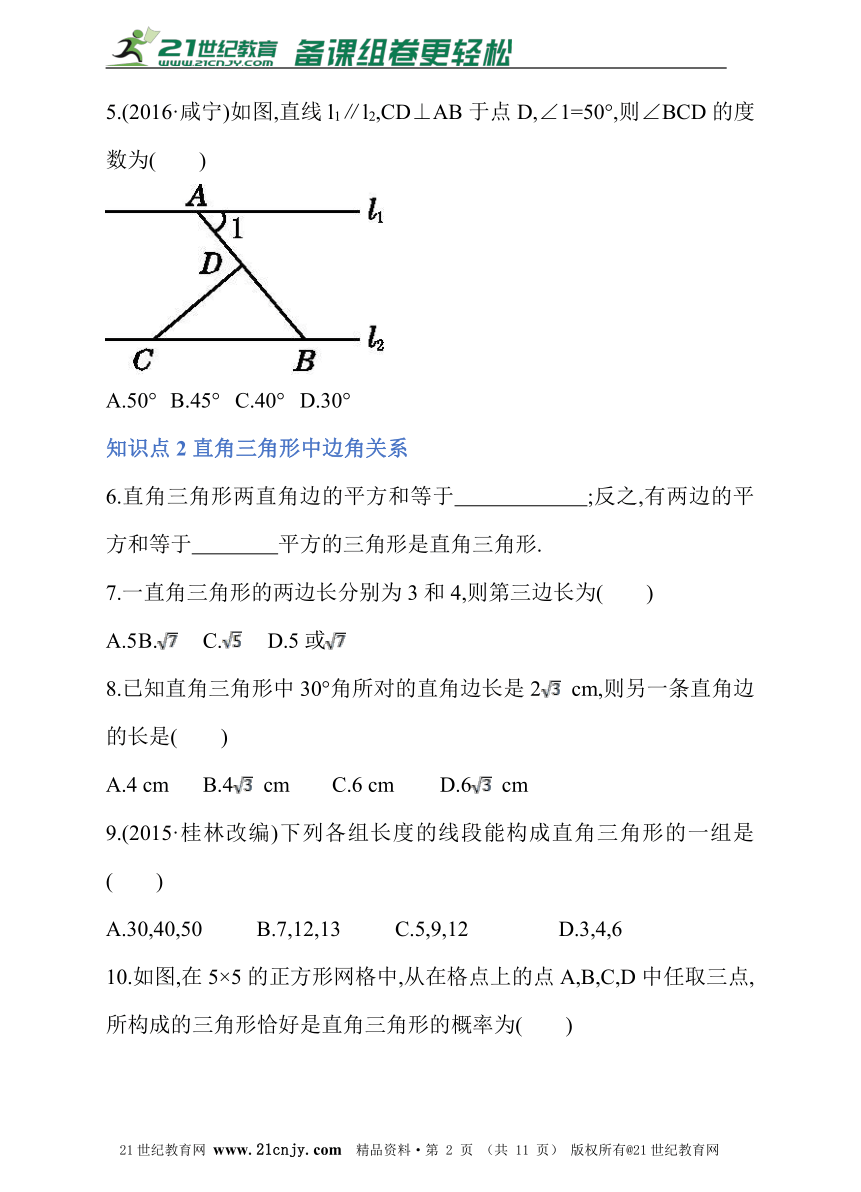
知识点2直角三角形中边角关系
6.直角三角形两直角边的平方和等于 ;反之,有两边的平方和等于 平方的三角形是直角三角形.?www.21-cn-jy.com
7.一直角三角形的两边长分别为3和4,则第三边长为( )
A.5 B. C. D.5或
8.已知直角三角形中30°角所对的直角边长是2 cm,则另一条直角边的长是( )
A.4 cm B.4 cm C.6 cm D.6 cm
9.(2015·桂林改编)下列各组长度的线段能构成直角三角形的一组是( )
A.30,40,50 B.7,12,13 C.5,9,12 D.3,4,6
10.如图,在5×5的正方形网格中,从在格点上的点A,B,C,D中任取三点,所构成的三角形恰好是直角三角形的概率为( )2·1·c·n·j·y
A. B. C. D.
11.△ABC的三边长分别为a,b,c,下列条件:
①∠A=∠B-∠C;
②∠A∶∠B∶∠C=3∶4∶5;
③a2=(b+c)(b-c);
④a∶b∶c=5∶12∶13,
其中能判定△ABC是直角三角形的有( )
A.1个 B.2个 C.3个 D.4个
12.(2016·南京)下列长度的三条线段能组成钝角三角形的是( )
A.3,4,4 B.3,4,5 C.3,4,6 D.3,4,7
知识点3互逆命题和互逆定理
13.逆命题的定义:如果两个命题的题设和结论刚好相反,那么这样的两个命题叫做 ,如果把其中一个命题叫做原命题,那么另一个叫做它的 .?【来源:21·世纪·教育·网】
14.逆定理的定义:一般地,如果一个定理的逆命题经过证明是正确的,那么它也是一个定理,称这两个定理互为 .?21·世纪*教育网
15.写出命题“如果a=b,那么3a=3b”的逆命
题: .?
16.下列命题的逆命题正确的是( )
A.两条直线平行,内错角相等
B.若两个实数相等,则它们的绝对值相等
C.全等三角形的对应角相等
D.若两个实数相等,则它们的平方也相等
17.下列定理有逆定理的是( )
A.同角的余角相等
B.线段垂直平分线上的点到线段两端点的距离相等
C.全等三角形的对应角相等
D.对顶角相等
培优检测
题型1直角三角形角的关系在求角中的应用
18.如图,在△ABC中,CD是∠ACB的平分线,CE是AB边上的高.
(1)若∠A=40°,∠B=72°,求∠DCE的度数;
(2)试写出∠DCE与∠A,∠B之间的数量关系,并证明.
题型2倍长中线法在构造直角三角形中的应用
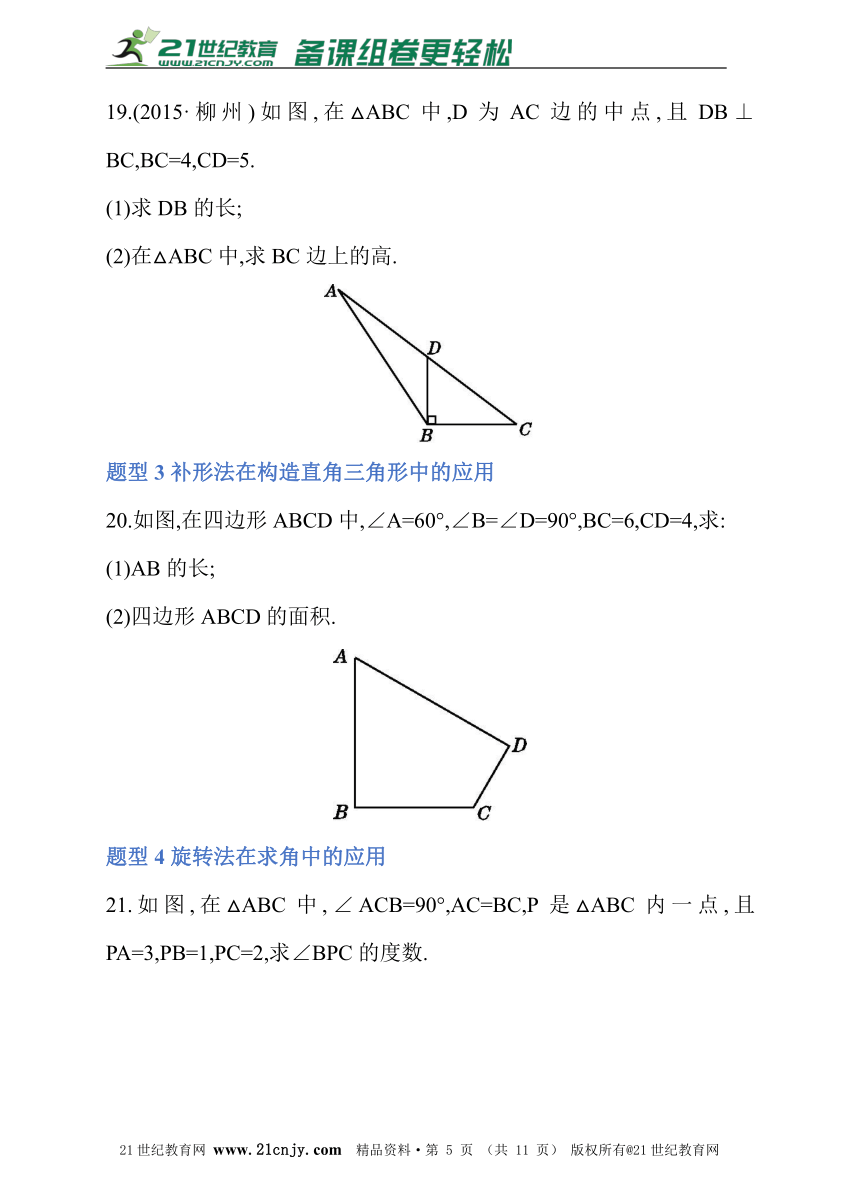
19.(2015·柳州)如图,在△ABC中,D为AC边的中点,且DB⊥BC,BC=4,CD=5.
(1)求DB的长;
(2)在△ABC中,求BC边上的高.
题型3补形法在构造直角三角形中的应用
20.如图,在四边形ABCD中,∠A=60°,∠B=∠D=90°,BC=6,CD=4,求:
(1)AB的长;
(2)四边形ABCD的面积.
题型4旋转法在求角中的应用
21.如图,在△ABC中,∠ACB=90°,AC=BC,P是△ABC内一点,且PA=3,PB=1,PC=2,求∠BPC的度数. 2-1-c-n-j-y
参考答案
1.【答案】互余;直角三角形
2.【答案】B
3.【答案】A
解:∠A+∠B=∠C(1)
∠A+∠B+∠C=180(2)
联立(1)(2)解得∠C=90
则得出△ABC为直角三角形 ! 选A
4.【答案】C
解:∵AB∥CD,
∴∠BEF=180-∠EFD=120°;
∵FP平分∠EFD,且∠EFD=60°,
∴∠EFP=30°,
在△EFP中,EP⊥FP,
∴∠FEP=60°;
∴∠BEP=∠BEF-∠FEP=60度.选C
5.【答案】C
解:∵l1∥l2,?∴∠ABC=∠1=50°;又∵CD⊥AB,?∴∠CDB=90°;?在△BCD中,∠BCD=180°-∠CDB-∠ABC=180°-90°-50°=40°?故选C.
6.【答案】斜边的平方;第三边
7.【答案】D
解:当已知边3和4都是直角边,则第三边是斜边,长是;当已知边3和4一条是直角边一条是斜边时,则第三边是直角边长是:=.故选D.21·cn·jy·com
8.【答案】C
9.【答案】A
解:∵30+40=50,∴该三角形符合勾股定理的逆定理,故是直角三角形,故选A
10.【答案】D
解:∵从点A,B,C,D中任取三点能组成三角形的一共有4种可能,其中△ABD,△ADC,△ABC是直角三角形,∴所构成的三角形恰好是直角三角形的概率为.故选D.www-2-1-cnjy-com
11.【答案】C
解:①∠A=∠B-∠C,∠A+∠B+∠C=180°,解得∠B=90°,故①是直角三角形;②∠A:∠B:∠C=3:4:5,∠A+∠B+∠C=180°,解得∠A=45°,∠B=60°,∠C=75°,故②不是直角三角形;③∵a2=(b+c)(b-c),∴a2+c2=b2,符合勾股定理的逆定理,故③是直角三角形;④∵a:b:c=5:12:13,∴a2+b2=c2,符合勾股定理的逆定理,故④是直角三角形.能判断△ABC是直角三角形的个数有3个;故选:C.
12.【答案】C
13.【答案】互逆命题;逆命题
14.【答案】逆定理
15.【答案】如果3a=3b,那么a=b
解:命题“如果”“a=b”那么“3a=3b”的逆命题是:如果3a=3b,那a=b,故答案为:如果3a=3b,那么a=b.21世纪教育网版权所有
16.【答案】A
解:逆命题:如果两个实数的绝对值相等,那么这两个实数相等.
不一定成立,如它们的绝对值相等,但一正一负,则这两个实数不相等.所以选A。
17.【答案】B
解:线段垂直平分线上的点到线段两端的距离相等
(到线段两端点距离相等的点在这线段的垂直平分线上.)故选B
18.解:(1)∵∠A=40°,∠B=72°,
∴∠ACB=180°-∠A-∠B=68°.
∵CD是∠ACB的平分线,
∴∠BCD=∠ACB=34°.
又∵CE⊥AB,∠B=72°,
∴∠BCE=18°.
∴∠DCE=∠BCD-∠BCE=16°.
(2)∠DCE=(∠B-∠A).
证明:∠DCE=90°-∠CDE=90°-(∠A+∠ACD)=90°-=90°-∠A+×(180°-∠A-∠B)=90°-=(∠B-∠A).
19.解:(1)∵DB⊥BC,BC=4,CD=5,∴DB==3.
(2)如图,延长BD至E.使DE=BD,连接AE.
∵D是AC的中点,
∴AD=DC.
在△BDC和△EDA中,
∴△BDC≌△EDA(SAS).
∴∠CAE=∠BCD.
∴AE∥BC.
∵DB⊥BC,∴BE⊥AE.
∴BE等于△ABC中BC边上的高.∴BE=2BD=6.
20.解:(1)如图,延长AD,BC交于点E.
在Rt△ABE中,∠A=60°,∴∠E=30°.
在Rt△CDE中,CD=4,∴CE=2CD=8.
∴BE=BC+CE=6+8=14.
设AB=x,则AE=2x,根据勾股定理得:x2+142=(2x)2,解得x=,则AB=.
(2)在Rt△CDE中,∠CDE=90°,
∴DE===4.
∴S四边形ABCD=S△ABE-S△CDE=·AB·BE-·CD·DE=××14-×4×4=.
21.解:如图,将△CPB绕点C顺时针旋转90°,得△CP'A,
则P'C=PC=2,P'A=PB=1.
连接PP',易知∠PCP'=90°,
∴PP'2=22+22=8.
又P'A=1,PA=3,而PP'2+P'A2=8+1=9,PA2=9,
∴PP'2+P'A2=PA2.
∴∠AP'P=90°.
又∠CP'P=45°,
∴∠BPC=∠CP'A=135°.
第1课时 直角三角形的性质与判定
基础检测
知识点1直角三角形中角的关系
1.直角三角形两锐角 ;反之,两锐角互余的三角形是 .?
2.如图,AD是Rt△ABC的斜边BC上的高,则图中与∠B互余的角有( )
A.1个 B.2个 C.3个 D.4个
3.在△ABC中,已知∠A+∠B=∠C,则△ABC是( )
A.直角三角形 B.锐角三角形 C.钝角三角形 D.无法确定
4.如图,若AB∥CD,EF与AB、CD分别相交于点E、F,EP与∠EFD的平分线FP相交于点P,且∠EFD=60°,EP⊥FP,则∠BEP=______度.21教育网
A.70° B.65° C.60° D.55°
5.(2016·咸宁)如图,直线l1∥l2,CD⊥AB于点D,∠1=50°,则∠BCD的度数为( )21cnjy.com
A.50° B.45° C.40° D.30°
知识点2直角三角形中边角关系
6.直角三角形两直角边的平方和等于 ;反之,有两边的平方和等于 平方的三角形是直角三角形.?www.21-cn-jy.com
7.一直角三角形的两边长分别为3和4,则第三边长为( )
A.5 B. C. D.5或
8.已知直角三角形中30°角所对的直角边长是2 cm,则另一条直角边的长是( )
A.4 cm B.4 cm C.6 cm D.6 cm
9.(2015·桂林改编)下列各组长度的线段能构成直角三角形的一组是( )
A.30,40,50 B.7,12,13 C.5,9,12 D.3,4,6
10.如图,在5×5的正方形网格中,从在格点上的点A,B,C,D中任取三点,所构成的三角形恰好是直角三角形的概率为( )2·1·c·n·j·y
A. B. C. D.
11.△ABC的三边长分别为a,b,c,下列条件:
①∠A=∠B-∠C;
②∠A∶∠B∶∠C=3∶4∶5;
③a2=(b+c)(b-c);
④a∶b∶c=5∶12∶13,
其中能判定△ABC是直角三角形的有( )
A.1个 B.2个 C.3个 D.4个
12.(2016·南京)下列长度的三条线段能组成钝角三角形的是( )
A.3,4,4 B.3,4,5 C.3,4,6 D.3,4,7
知识点3互逆命题和互逆定理
13.逆命题的定义:如果两个命题的题设和结论刚好相反,那么这样的两个命题叫做 ,如果把其中一个命题叫做原命题,那么另一个叫做它的 .?【来源:21·世纪·教育·网】
14.逆定理的定义:一般地,如果一个定理的逆命题经过证明是正确的,那么它也是一个定理,称这两个定理互为 .?21·世纪*教育网
15.写出命题“如果a=b,那么3a=3b”的逆命
题: .?
16.下列命题的逆命题正确的是( )
A.两条直线平行,内错角相等
B.若两个实数相等,则它们的绝对值相等
C.全等三角形的对应角相等
D.若两个实数相等,则它们的平方也相等
17.下列定理有逆定理的是( )
A.同角的余角相等
B.线段垂直平分线上的点到线段两端点的距离相等
C.全等三角形的对应角相等
D.对顶角相等
培优检测
题型1直角三角形角的关系在求角中的应用
18.如图,在△ABC中,CD是∠ACB的平分线,CE是AB边上的高.
(1)若∠A=40°,∠B=72°,求∠DCE的度数;
(2)试写出∠DCE与∠A,∠B之间的数量关系,并证明.
题型2倍长中线法在构造直角三角形中的应用
19.(2015·柳州)如图,在△ABC中,D为AC边的中点,且DB⊥BC,BC=4,CD=5.
(1)求DB的长;
(2)在△ABC中,求BC边上的高.
题型3补形法在构造直角三角形中的应用
20.如图,在四边形ABCD中,∠A=60°,∠B=∠D=90°,BC=6,CD=4,求:
(1)AB的长;
(2)四边形ABCD的面积.
题型4旋转法在求角中的应用
21.如图,在△ABC中,∠ACB=90°,AC=BC,P是△ABC内一点,且PA=3,PB=1,PC=2,求∠BPC的度数. 2-1-c-n-j-y
参考答案
1.【答案】互余;直角三角形
2.【答案】B
3.【答案】A
解:∠A+∠B=∠C(1)
∠A+∠B+∠C=180(2)
联立(1)(2)解得∠C=90
则得出△ABC为直角三角形 ! 选A
4.【答案】C
解:∵AB∥CD,
∴∠BEF=180-∠EFD=120°;
∵FP平分∠EFD,且∠EFD=60°,
∴∠EFP=30°,
在△EFP中,EP⊥FP,
∴∠FEP=60°;
∴∠BEP=∠BEF-∠FEP=60度.选C
5.【答案】C
解:∵l1∥l2,?∴∠ABC=∠1=50°;又∵CD⊥AB,?∴∠CDB=90°;?在△BCD中,∠BCD=180°-∠CDB-∠ABC=180°-90°-50°=40°?故选C.
6.【答案】斜边的平方;第三边
7.【答案】D
解:当已知边3和4都是直角边,则第三边是斜边,长是;当已知边3和4一条是直角边一条是斜边时,则第三边是直角边长是:=.故选D.21·cn·jy·com
8.【答案】C
9.【答案】A
解:∵30+40=50,∴该三角形符合勾股定理的逆定理,故是直角三角形,故选A
10.【答案】D
解:∵从点A,B,C,D中任取三点能组成三角形的一共有4种可能,其中△ABD,△ADC,△ABC是直角三角形,∴所构成的三角形恰好是直角三角形的概率为.故选D.www-2-1-cnjy-com
11.【答案】C
解:①∠A=∠B-∠C,∠A+∠B+∠C=180°,解得∠B=90°,故①是直角三角形;②∠A:∠B:∠C=3:4:5,∠A+∠B+∠C=180°,解得∠A=45°,∠B=60°,∠C=75°,故②不是直角三角形;③∵a2=(b+c)(b-c),∴a2+c2=b2,符合勾股定理的逆定理,故③是直角三角形;④∵a:b:c=5:12:13,∴a2+b2=c2,符合勾股定理的逆定理,故④是直角三角形.能判断△ABC是直角三角形的个数有3个;故选:C.
12.【答案】C
13.【答案】互逆命题;逆命题
14.【答案】逆定理
15.【答案】如果3a=3b,那么a=b
解:命题“如果”“a=b”那么“3a=3b”的逆命题是:如果3a=3b,那a=b,故答案为:如果3a=3b,那么a=b.21世纪教育网版权所有
16.【答案】A
解:逆命题:如果两个实数的绝对值相等,那么这两个实数相等.
不一定成立,如它们的绝对值相等,但一正一负,则这两个实数不相等.所以选A。
17.【答案】B
解:线段垂直平分线上的点到线段两端的距离相等
(到线段两端点距离相等的点在这线段的垂直平分线上.)故选B
18.解:(1)∵∠A=40°,∠B=72°,
∴∠ACB=180°-∠A-∠B=68°.
∵CD是∠ACB的平分线,
∴∠BCD=∠ACB=34°.
又∵CE⊥AB,∠B=72°,
∴∠BCE=18°.
∴∠DCE=∠BCD-∠BCE=16°.
(2)∠DCE=(∠B-∠A).
证明:∠DCE=90°-∠CDE=90°-(∠A+∠ACD)=90°-=90°-∠A+×(180°-∠A-∠B)=90°-=(∠B-∠A).
19.解:(1)∵DB⊥BC,BC=4,CD=5,∴DB==3.
(2)如图,延长BD至E.使DE=BD,连接AE.
∵D是AC的中点,
∴AD=DC.
在△BDC和△EDA中,
∴△BDC≌△EDA(SAS).
∴∠CAE=∠BCD.
∴AE∥BC.
∵DB⊥BC,∴BE⊥AE.
∴BE等于△ABC中BC边上的高.∴BE=2BD=6.
20.解:(1)如图,延长AD,BC交于点E.
在Rt△ABE中,∠A=60°,∴∠E=30°.
在Rt△CDE中,CD=4,∴CE=2CD=8.
∴BE=BC+CE=6+8=14.
设AB=x,则AE=2x,根据勾股定理得:x2+142=(2x)2,解得x=,则AB=.
(2)在Rt△CDE中,∠CDE=90°,
∴DE===4.
∴S四边形ABCD=S△ABE-S△CDE=·AB·BE-·CD·DE=××14-×4×4=.
21.解:如图,将△CPB绕点C顺时针旋转90°,得△CP'A,
则P'C=PC=2,P'A=PB=1.
连接PP',易知∠PCP'=90°,
∴PP'2=22+22=8.
又P'A=1,PA=3,而PP'2+P'A2=8+1=9,PA2=9,
∴PP'2+P'A2=PA2.
∴∠AP'P=90°.
又∠CP'P=45°,
∴∠BPC=∠CP'A=135°.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
