山东省日照市2016-2017学年度八年级上学期数学期末检测试卷(含答案)
文档属性
| 名称 | 山东省日照市2016-2017学年度八年级上学期数学期末检测试卷(含答案) | 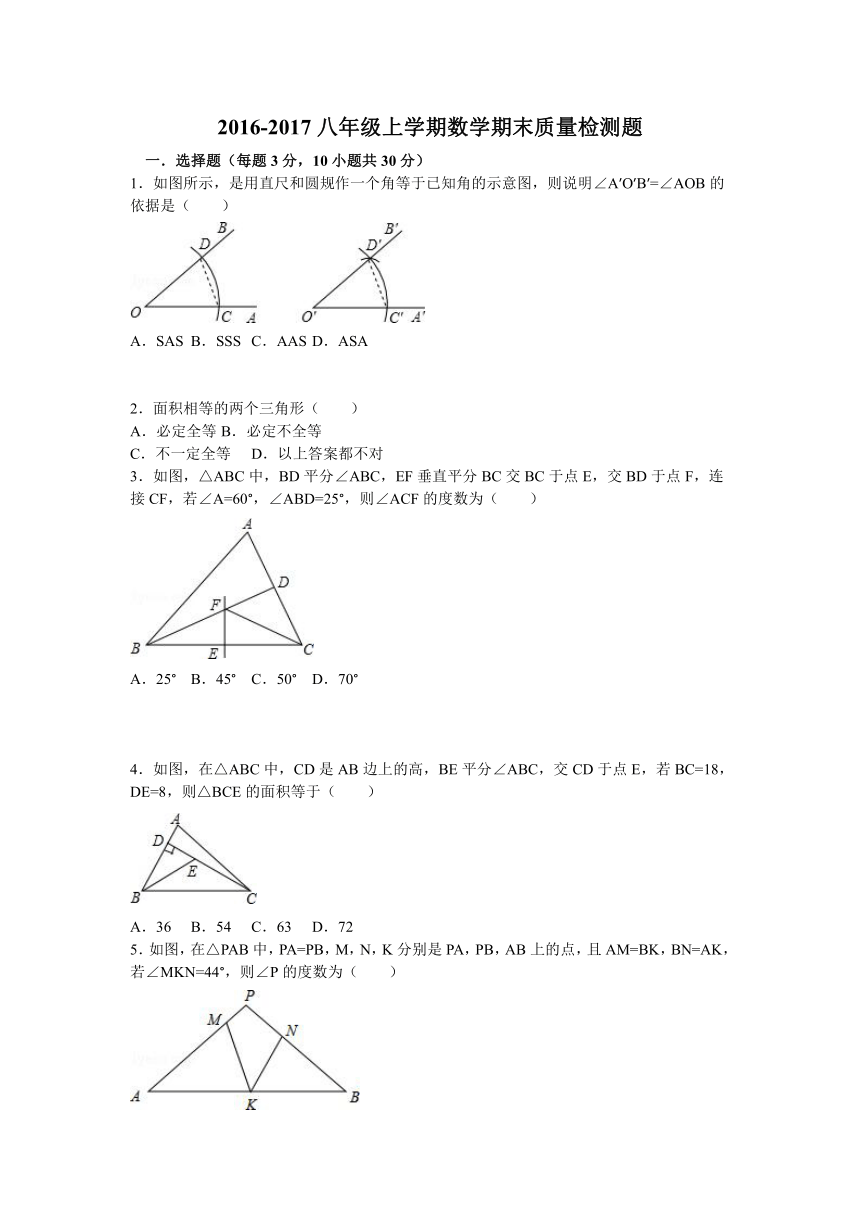 | |
| 格式 | zip | ||
| 文件大小 | 89.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-07 14:47:14 | ||
图片预览



文档简介
2016-2017八年级上学期数学期末质量检测题
一.选择题(每题3分,10小题共30分)
1.如图所示,是用直尺和圆规作一个角等于已知角的示意图,则说明∠A′O′B′=∠AOB的依据是( )
A.SAS
B.SSS
C.AAS
D.ASA
2.面积相等的两个三角形( )
A.必定全等
B.必定不全等
C.不一定全等
D.以上答案都不对
3.如图,△ABC中,BD平分∠ABC,EF垂直平分BC交BC于点E,交BD于点F,连接CF,若∠A=60°,∠ABD=25°,则∠ACF的度数为( )
A.25°
B.45°
C.50°
D.70°
4.如图,在△ABC中,CD是AB边上的高,BE平分∠ABC,交CD于点E,若BC=18,DE=8,则△BCE的面积等于( )
A.36
B.54
C.63
D.72
5.如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=44°,则∠P的度数为( )
A.44°
B.66°
C.88°
D.92°
6.如图,D是直角△ABC斜边BC上一点,AB=AD,记∠CAD=α,∠ABC=β.若α=10°,则β的度数是( )
A.40°
B.50°
C.60°
D.不能确定
7.已知分式的值为0,那么x的值是( )
A.﹣1
B.﹣2
C.1
D.1或﹣2
8.若分式中的a、b的值同时扩大到原来的10倍,则分式的值( )
A.是原来的20倍
B.是原来的10倍
C.是原来的0.1倍
D.不变
9.已知一组数据:60,30,40,50,70,这组数据的平均数和中位数分别是( )
A.60,50
B.50,60
C.50,50
D.60,60
10.某校九年级(1)班全体学生2016年初中毕业体育考试的成绩统计如表:
成绩(分)
35
39
42
44
45
48
50
人数(人)
2
5
6
6
8
7
6
根据表中的信息判断,下列结论中错误的是( )
A.该班一共有40名同学
B.该班学生这次考试成绩的众数是45分
C.该班学生这次考试成绩的中位数是45分
D.该班学生这次考试成绩的平均数是45分
二.填空题(每题3分,5小题共15分)
11.如图,在△ABC中,AB=10,AC=8,O为△ABC角平分线的交点,若△ABO的面积为20,则△ACO的面积为 .
12.如图,∠BAC=110°,若MP和NQ分别垂直平分AB和AC,则∠PAQ的度数是 .
13.已知点A(3,3)和点B是平面内两点,且它们关于直线x=2轴对称,则点B的坐标为 .
14.计算22,24,26,28,30这组数据的方差是 .
15.等腰三角形一腰上的高与另一腰的夹角为48°,则该等腰三角形的底角的度数为 .
三、解答题(共75分)
16、(每题5分,共20分)(1).化简:.
(2).化简:(1+)÷.
(3).若关于x的分式方程有增根,求m的值.
(4).已知a:b:c=2:3:4,且2a+3b﹣2c=10,求a,b,c的值.
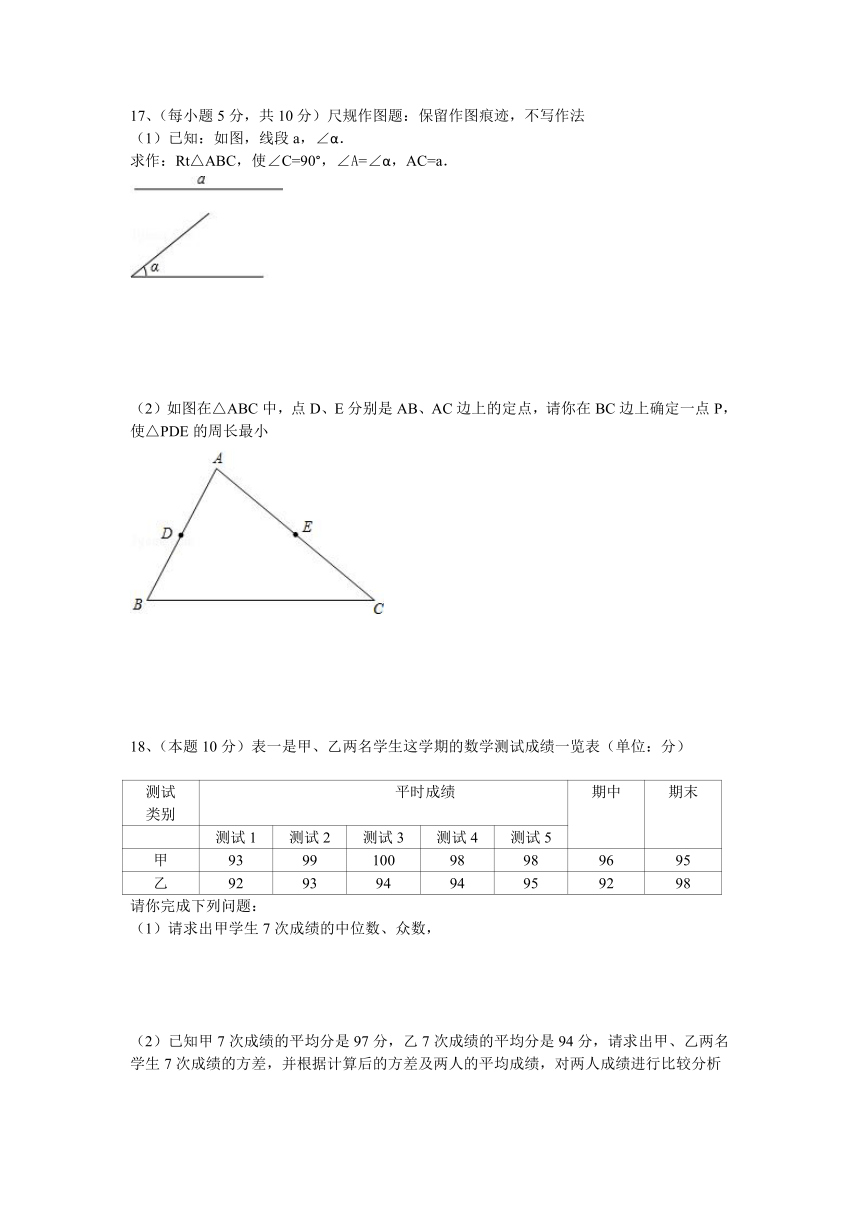
17、(每小题5分,共10分)尺规作图题:保留作图痕迹,不写作法
(1)已知:如图,线段a,∠α.
求作:Rt△ABC,使∠C=90°,∠A=∠α,AC=a.
(2)如图在△ABC中,点D、E分别是AB、AC边上的定点,请你在BC边上确定一点P,使△PDE的周长最小
18、(本题10分)表一是甲、乙两名学生这学期的数学测试成绩一览表(单位:分)
测试
类别
平时成绩
期中
期末
测试1
测试2
测试3
测试4
测试5
甲
93
99
100
98
98
96
95
乙
92
93
94
94
95
92
98
请你完成下列问题:
(1)请求出甲学生7次成绩的中位数、众数,
(2)已知甲7次成绩的平均分是97分,乙7次成绩的平均分是94分,请求出甲、乙两名学生7次成绩的方差,并根据计算后的方差及两人的平均成绩,对两人成绩进行比较分析
(3)已知甲平时成绩的平均分是97.6分,乙平时成绩的平均分是93.6分,学校规定:学生平时成绩的平均数、期中成绩、期末成绩三项分别按40%、20%、40%的比例计入学期总评成绩,这两名学生的期末总评成绩是多少?
19、(本题10分)五月初,我市多地遭遇了持续强降雨的恶劣天气,造成部分地区出现严重洪涝灾害,某爱心组织紧急筹集了部分资金,计划购买甲、乙两种救灾物品共2000件送往灾区,已知每件甲种物品的价格比每件乙种物品的价格贵10元,用350元购买甲种物品的件数恰好与用300元购买乙种物品的件数相同
(1)求甲、乙两种救灾物品每件的价格各是多少元?
(2)经调查,灾区对乙种物品件数的需求量是甲种物品件数的3倍,若该爱心组织按照此需求的比例购买这2000件物品,需筹集资金多少元?
20、(本题8分)如图,OM平分∠POQ,MA⊥OP,MB⊥OQ,A、B为垂足,AB交OM于点N.
求证:AN=BN
21、(本题8分)如图:△ABC中,BE⊥AC,CF⊥AB,BM=AC,CN=AB。求证:(1)AM=AN;(2)AM⊥AN。
打字员注意:把上图的大小不变,重新画个线段不带锯齿的。注意要把这俩条件画准:(1)AM=AN;(2)AM⊥AN。
22、(本题9分)如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形.BE交AC于F,AD交CE于H.
(1)求证:△BCE≌△ACD;
(2)求证:FH∥BD.
2016-2017八年级上学期数学期末质量检测题
参考答案及评分标准
选择题:(每题3分,共30分)
B
2、C
3、B
4、D
5、D
6、B
7、B
8、B
9、C
10、D
填空题:(每题3分,共15分)
11、16
12、40°
13、点B(1,3)
14、8
15、69°或21°
解答题:
16、(每题5分,共20分)(1)解:
=++2=++2=++
=……………………2分
=……………………5分
注意:此题分母为x(x+2)或x2+2x均不扣分
(2)解:原式=a-1……………………5分
此题最后结果不对就不再给过程分
m=-2……………………5分
此题最后结果不对就不再给过程分
(4)
解:设a=2k,b=3k,c=4k,
又∵2a+3b﹣2c=10,∴4k+9k﹣8k=10,
5k=10,解得k=2.……………………3分
∴a=4,b=6,c=8.……………………5分
17、(每小题5分,共10分)解:(1)如图,△ABC为所作.
评分标准:本题满分5分,1、在已知角上直接作图的不得分2、没有垂直作图痕迹的扣2分3、作角痕迹不对的扣2分
4、不写结论扣1分,仅有结论不得分。
(2)解:如图所示:
评分标准:本题满分5分,1、参考答案的图形没有作垂直的痕迹,没有垂直作图痕迹的扣2分
2、不写结论扣1分,仅有结论不得分。
18、(本题10分)(1)甲学生7次成绩的中位数是98、众数是98
………………2分
(2)甲七次成绩的方差是S2甲=5,乙七次成绩的方差是S2乙=3.7,……………………4分
甲成绩波动大,乙成绩波动小;……………………6分
但是甲平均分高于乙,说明几次考试的总体水平甲高于乙……………………8分
(3)甲96.24
乙95.04……………………10分
19、(本题10分)解:(1)设每件乙种物品的价格是x元,则每件甲种物品的价格是(x+10)元,根据题意得,=,……………………3分
解得:x=60.……………………4分
经检验,x=60是原方程的解.……………………5分
答:甲、乙两种救灾物品每件的价格各是70元、60元;……………………6分
(2)设甲种物品件数为m件,则乙种物品件数为3m件,
根据题意得,m+3m=2000,
解得m=500,……………………7分
即甲种物品件数为500件,则乙种物品件数为1500件,
此时需筹集资金:70×500+60×1500=125000(元).……………………9分
答:若该爱心组织按照此需求的比例购买这2000件物品,需筹集资金125000元.……………………10分
其它方法只要合理都要酌情给分!
20、(本题8分)证明:
∵OM平分∠POQ∴∠POM=∠QOM……………………1分
∵MA⊥OP,MB⊥OQ
∴∠MAO=∠MBO=90……………………2分
∵OM=OM
∴△AOM≌△BOM
(AAS)……………………4分
∴OA=OB……………………5分
∵ON=ON
∴△AON≌△BON
(SAS)……………………7分
∴AN=BN……………………8分
其它方法只要合理都要酌情给分!
21、(本题8分)证明:(1)∵BE⊥AC,CF⊥AB
∴∠ABM+∠BAC=90°,∠ACN+∠BAC=90°
∴∠ABM=∠ACN……………………2分
∵BM=AC,CN=AB
∴△ABM≌△NAC……………………4分
∴AM=AN……………………5分
(2)∵△ABM≌△NAC
∴∠BAM=∠N……………………6分
∵∠N+∠BAN=90°
∴∠BAM+∠BAN=90°……………………7分
即∠MAN=90°
∴AM⊥AN……………………8分
其它方法只要合理都要酌情给分!
22、(本题9分)证明:(1)∵△ABC和△CDE都是等边三角形,
∴BC=AC,CE=CD,∠BCA=∠ECD=60°,……………………1分
∴∠BCA+∠ACE=∠ECD+∠ACE,即∠BCE=∠ACD,……………………2分
∴在△BCE和△ACD中,
∵,
∴△BCE≌△ACD
(SAS).……………………4分
(2)由(1)知△BCE≌△ACD,
则∠CBF=∠CAH,BC=AC……………………5分
又∵△ABC和△CDE都是等边三角形,且点B、C、D在同一条直线上,
∴∠ACH=180°﹣∠ACB﹣∠HCD=60°=∠BCF,
在△BCF和△ACH中,
∵,
∴△BCF≌△ACH
(ASA),……………………7分
∴CF=CH,……………………8分
又∵∠FCH=60°,
∴△CHF为等边三角形
∴∠FHC=∠HCD=60°,
∴FH∥BD.……………………9分
其它方法只要合理都要酌情给分!
一.选择题(每题3分,10小题共30分)
1.如图所示,是用直尺和圆规作一个角等于已知角的示意图,则说明∠A′O′B′=∠AOB的依据是( )
A.SAS
B.SSS
C.AAS
D.ASA
2.面积相等的两个三角形( )
A.必定全等
B.必定不全等
C.不一定全等
D.以上答案都不对
3.如图,△ABC中,BD平分∠ABC,EF垂直平分BC交BC于点E,交BD于点F,连接CF,若∠A=60°,∠ABD=25°,则∠ACF的度数为( )
A.25°
B.45°
C.50°
D.70°
4.如图,在△ABC中,CD是AB边上的高,BE平分∠ABC,交CD于点E,若BC=18,DE=8,则△BCE的面积等于( )
A.36
B.54
C.63
D.72
5.如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=44°,则∠P的度数为( )
A.44°
B.66°
C.88°
D.92°
6.如图,D是直角△ABC斜边BC上一点,AB=AD,记∠CAD=α,∠ABC=β.若α=10°,则β的度数是( )
A.40°
B.50°
C.60°
D.不能确定
7.已知分式的值为0,那么x的值是( )
A.﹣1
B.﹣2
C.1
D.1或﹣2
8.若分式中的a、b的值同时扩大到原来的10倍,则分式的值( )
A.是原来的20倍
B.是原来的10倍
C.是原来的0.1倍
D.不变
9.已知一组数据:60,30,40,50,70,这组数据的平均数和中位数分别是( )
A.60,50
B.50,60
C.50,50
D.60,60
10.某校九年级(1)班全体学生2016年初中毕业体育考试的成绩统计如表:
成绩(分)
35
39
42
44
45
48
50
人数(人)
2
5
6
6
8
7
6
根据表中的信息判断,下列结论中错误的是( )
A.该班一共有40名同学
B.该班学生这次考试成绩的众数是45分
C.该班学生这次考试成绩的中位数是45分
D.该班学生这次考试成绩的平均数是45分
二.填空题(每题3分,5小题共15分)
11.如图,在△ABC中,AB=10,AC=8,O为△ABC角平分线的交点,若△ABO的面积为20,则△ACO的面积为 .
12.如图,∠BAC=110°,若MP和NQ分别垂直平分AB和AC,则∠PAQ的度数是 .
13.已知点A(3,3)和点B是平面内两点,且它们关于直线x=2轴对称,则点B的坐标为 .
14.计算22,24,26,28,30这组数据的方差是 .
15.等腰三角形一腰上的高与另一腰的夹角为48°,则该等腰三角形的底角的度数为 .
三、解答题(共75分)
16、(每题5分,共20分)(1).化简:.
(2).化简:(1+)÷.
(3).若关于x的分式方程有增根,求m的值.
(4).已知a:b:c=2:3:4,且2a+3b﹣2c=10,求a,b,c的值.
17、(每小题5分,共10分)尺规作图题:保留作图痕迹,不写作法
(1)已知:如图,线段a,∠α.
求作:Rt△ABC,使∠C=90°,∠A=∠α,AC=a.
(2)如图在△ABC中,点D、E分别是AB、AC边上的定点,请你在BC边上确定一点P,使△PDE的周长最小
18、(本题10分)表一是甲、乙两名学生这学期的数学测试成绩一览表(单位:分)
测试
类别
平时成绩
期中
期末
测试1
测试2
测试3
测试4
测试5
甲
93
99
100
98
98
96
95
乙
92
93
94
94
95
92
98
请你完成下列问题:
(1)请求出甲学生7次成绩的中位数、众数,
(2)已知甲7次成绩的平均分是97分,乙7次成绩的平均分是94分,请求出甲、乙两名学生7次成绩的方差,并根据计算后的方差及两人的平均成绩,对两人成绩进行比较分析
(3)已知甲平时成绩的平均分是97.6分,乙平时成绩的平均分是93.6分,学校规定:学生平时成绩的平均数、期中成绩、期末成绩三项分别按40%、20%、40%的比例计入学期总评成绩,这两名学生的期末总评成绩是多少?
19、(本题10分)五月初,我市多地遭遇了持续强降雨的恶劣天气,造成部分地区出现严重洪涝灾害,某爱心组织紧急筹集了部分资金,计划购买甲、乙两种救灾物品共2000件送往灾区,已知每件甲种物品的价格比每件乙种物品的价格贵10元,用350元购买甲种物品的件数恰好与用300元购买乙种物品的件数相同
(1)求甲、乙两种救灾物品每件的价格各是多少元?
(2)经调查,灾区对乙种物品件数的需求量是甲种物品件数的3倍,若该爱心组织按照此需求的比例购买这2000件物品,需筹集资金多少元?
20、(本题8分)如图,OM平分∠POQ,MA⊥OP,MB⊥OQ,A、B为垂足,AB交OM于点N.
求证:AN=BN
21、(本题8分)如图:△ABC中,BE⊥AC,CF⊥AB,BM=AC,CN=AB。求证:(1)AM=AN;(2)AM⊥AN。
打字员注意:把上图的大小不变,重新画个线段不带锯齿的。注意要把这俩条件画准:(1)AM=AN;(2)AM⊥AN。
22、(本题9分)如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形.BE交AC于F,AD交CE于H.
(1)求证:△BCE≌△ACD;
(2)求证:FH∥BD.
2016-2017八年级上学期数学期末质量检测题
参考答案及评分标准
选择题:(每题3分,共30分)
B
2、C
3、B
4、D
5、D
6、B
7、B
8、B
9、C
10、D
填空题:(每题3分,共15分)
11、16
12、40°
13、点B(1,3)
14、8
15、69°或21°
解答题:
16、(每题5分,共20分)(1)解:
=++2=++2=++
=……………………2分
=……………………5分
注意:此题分母为x(x+2)或x2+2x均不扣分
(2)解:原式=a-1……………………5分
此题最后结果不对就不再给过程分
m=-2……………………5分
此题最后结果不对就不再给过程分
(4)
解:设a=2k,b=3k,c=4k,
又∵2a+3b﹣2c=10,∴4k+9k﹣8k=10,
5k=10,解得k=2.……………………3分
∴a=4,b=6,c=8.……………………5分
17、(每小题5分,共10分)解:(1)如图,△ABC为所作.
评分标准:本题满分5分,1、在已知角上直接作图的不得分2、没有垂直作图痕迹的扣2分3、作角痕迹不对的扣2分
4、不写结论扣1分,仅有结论不得分。
(2)解:如图所示:
评分标准:本题满分5分,1、参考答案的图形没有作垂直的痕迹,没有垂直作图痕迹的扣2分
2、不写结论扣1分,仅有结论不得分。
18、(本题10分)(1)甲学生7次成绩的中位数是98、众数是98
………………2分
(2)甲七次成绩的方差是S2甲=5,乙七次成绩的方差是S2乙=3.7,……………………4分
甲成绩波动大,乙成绩波动小;……………………6分
但是甲平均分高于乙,说明几次考试的总体水平甲高于乙……………………8分
(3)甲96.24
乙95.04……………………10分
19、(本题10分)解:(1)设每件乙种物品的价格是x元,则每件甲种物品的价格是(x+10)元,根据题意得,=,……………………3分
解得:x=60.……………………4分
经检验,x=60是原方程的解.……………………5分
答:甲、乙两种救灾物品每件的价格各是70元、60元;……………………6分
(2)设甲种物品件数为m件,则乙种物品件数为3m件,
根据题意得,m+3m=2000,
解得m=500,……………………7分
即甲种物品件数为500件,则乙种物品件数为1500件,
此时需筹集资金:70×500+60×1500=125000(元).……………………9分
答:若该爱心组织按照此需求的比例购买这2000件物品,需筹集资金125000元.……………………10分
其它方法只要合理都要酌情给分!
20、(本题8分)证明:
∵OM平分∠POQ∴∠POM=∠QOM……………………1分
∵MA⊥OP,MB⊥OQ
∴∠MAO=∠MBO=90……………………2分
∵OM=OM
∴△AOM≌△BOM
(AAS)……………………4分
∴OA=OB……………………5分
∵ON=ON
∴△AON≌△BON
(SAS)……………………7分
∴AN=BN……………………8分
其它方法只要合理都要酌情给分!
21、(本题8分)证明:(1)∵BE⊥AC,CF⊥AB
∴∠ABM+∠BAC=90°,∠ACN+∠BAC=90°
∴∠ABM=∠ACN……………………2分
∵BM=AC,CN=AB
∴△ABM≌△NAC……………………4分
∴AM=AN……………………5分
(2)∵△ABM≌△NAC
∴∠BAM=∠N……………………6分
∵∠N+∠BAN=90°
∴∠BAM+∠BAN=90°……………………7分
即∠MAN=90°
∴AM⊥AN……………………8分
其它方法只要合理都要酌情给分!
22、(本题9分)证明:(1)∵△ABC和△CDE都是等边三角形,
∴BC=AC,CE=CD,∠BCA=∠ECD=60°,……………………1分
∴∠BCA+∠ACE=∠ECD+∠ACE,即∠BCE=∠ACD,……………………2分
∴在△BCE和△ACD中,
∵,
∴△BCE≌△ACD
(SAS).……………………4分
(2)由(1)知△BCE≌△ACD,
则∠CBF=∠CAH,BC=AC……………………5分
又∵△ABC和△CDE都是等边三角形,且点B、C、D在同一条直线上,
∴∠ACH=180°﹣∠ACB﹣∠HCD=60°=∠BCF,
在△BCF和△ACH中,
∵,
∴△BCF≌△ACH
(ASA),……………………7分
∴CF=CH,……………………8分
又∵∠FCH=60°,
∴△CHF为等边三角形
∴∠FHC=∠HCD=60°,
∴FH∥BD.……………………9分
其它方法只要合理都要酌情给分!
同课章节目录
