湖南省株洲市长鸿实验学校、南方中学、醴陵一中2016-2017学年高一(上)12月联考数学试卷(解析版)
文档属性
| 名称 | 湖南省株洲市长鸿实验学校、南方中学、醴陵一中2016-2017学年高一(上)12月联考数学试卷(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 342.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-01-21 10:01:36 | ||
图片预览




文档简介
2016-2017学年湖南省株洲市长鸿实验学校、南方中学、醴陵一中高一(上)12月联考数学试卷
一、单项选择题(本大题共12小题,每小题5分,共60分)
1.已知全集U={1,2,3,4,5},集合A={3,4},B={2,3,5},那么集合A∪( UB)等于( )
A.{1,2,3,4,5}
B.{3,4}
C.{1,3,4}
D.{2,3,4,5}
2.有下列命题:
①若直线l平行于平面α内的无数条直线,则直线l∥α:
②若直线a在平面α外.则a∥α:
③若直线a∥b,b∥α,则a∥α:
④若直线a∥b.b∥α.则a平行于平面α内的无数条直线.
其中真命题的个数是( )
A.1
B.2
C.3
D.4
3.函数f(x)=+log2(x+1)的定义域为( )
A.[1,3)
B.(
1,3)
C.(﹣1,3]
D.[﹣1,3]
4.某四棱锥的三视图如图所示,该四棱锥的表面积是( )
A.16
B.16+16
C.32
D.16+32
5.函数f(x)=2x+x﹣2的零点所在区间是( )
A.(﹣∞,﹣1)
B.(﹣l,0)
C.(0,1)
D.(1,2)
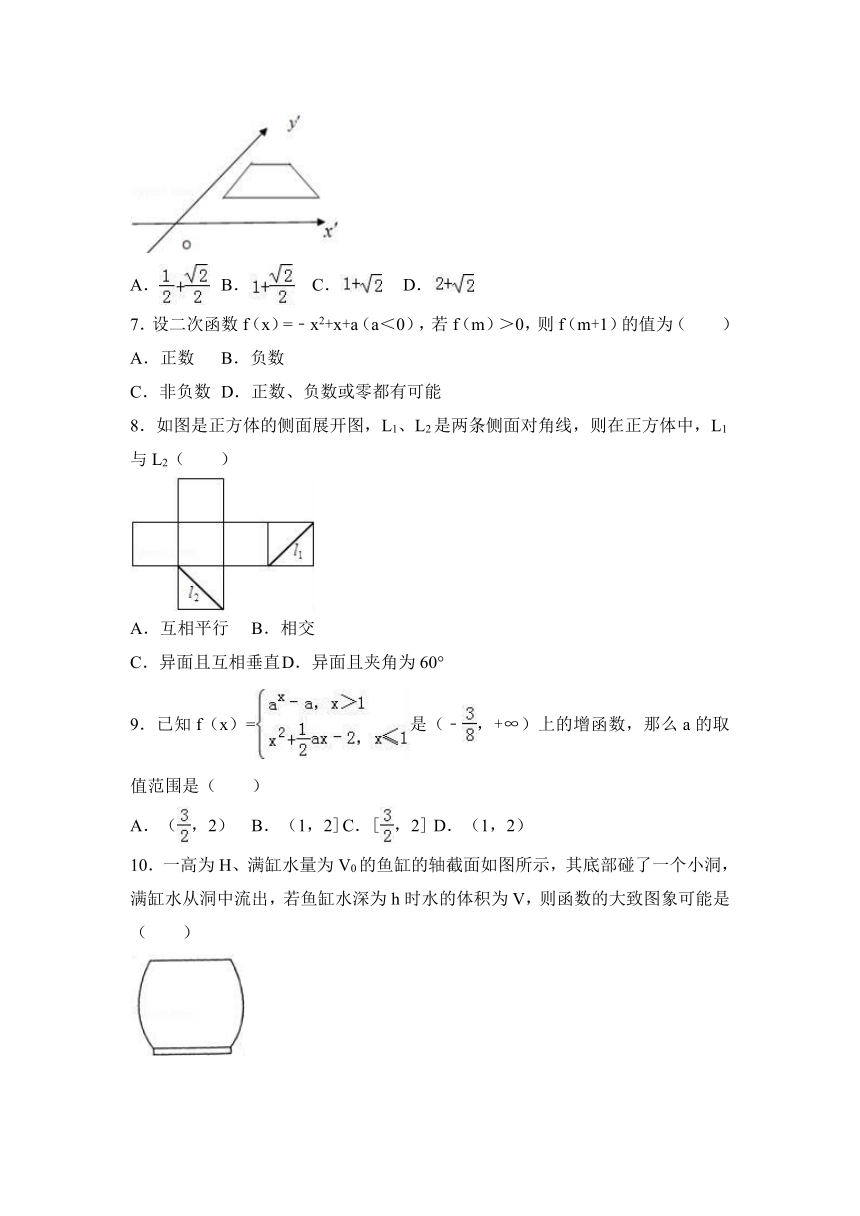
6.如图,一个水平放置的平面图形的斜二测直观图是一个底角为45°,腰和上底均为1的等腰梯形,那么原平面图形的面积是( )
A.
B.
C.
D.
7.设二次函数f(x)=﹣x2+x+a(a<0),若f(m)>0,则f(m+1)的值为( )
A.正数
B.负数
C.非负数
D.正数、负数或零都有可能
8.如图是正方体的侧面展开图,L1、L2是两条侧面对角线,则在正方体中,L1与L2( )
A.互相平行
B.相交
C.异面且互相垂直
D.异面且夹角为60°
9.已知f(x)=是(﹣,+∞)上的增函数,那么a的取值范围是( )
A.(,2)
B.(1,2]
C.[,2]
D.(1,2)
10.一高为H、满缸水量为V0的鱼缸的轴截面如图所示,其底部碰了一个小洞,满缸水从洞中流出,若鱼缸水深为h时水的体积为V,则函数的大致图象可能是( )
A.
B.
C.
D.
11.下列四个正方体图形中,A,B为正方体的两个顶点,M,N,P分别为其所在棱的中点,能得出AB∥平面MNP的图形的序号是( )
A.①、②
B.①、③
C.②、③
D.②、④
12.对于集合M、N,定义M﹣N={x|x∈M,且x N},M N=(M﹣N)∪(N﹣M).设A={y|y=x2﹣3x,x∈R},B={y|y=﹣2x,x∈R},则A B=( )
A.
B.
C.
D.
二、填空题(本大题共4小题,每小题5分,共20分,将答案填在题中的横线上.)
13.f(x)=,若f(x)=1,则x= .
14.若三棱锥P﹣ABC的侧棱长PA=PB=PC,则点P在底面的射影O是△ABC的 心.
15.函数f(x)是定义在(0,+∞)上的增函数,且满足f(a b)=f(a)+f(b),f(3)=1则不等式:f(x)﹣f(x﹣2)>3的解集为 .
16.如图,半径为4的球O中有一内接圆柱,当圆柱的侧面积最大时,球的表面积与该圆柱的侧面积之差是 .
三、解答题(本大题共6小题,共70分,解答应写出文字说明.证明过程或演算步骤)
17.已知函数f(x)是定义在R上的奇函数,当x≥0时,f(x)=x2﹣2x.
(1)求f(x)的解析式,并画出的f(x)图象;
(2)设g(x)=f(x)﹣k,利用图象求:当实数k为何值时,函数g(x)有三个零点.
18.设全集为U=R,集合A={x|(x+3)(4﹣x)≤0},B={x|log2(x+2)<3}.
(1)求A∩ UB;
(2)已知C={x|2a<x<a+1},若C A∪B,求实数a的取值范围.
19.已知四棱锥P﹣ABCD,底面ABCD是∠A=60°、边长为a的菱形,又PD⊥底面
ABCD,且PD=CD,点M、N分别是棱AD、PC的中点.
(1)证明:DN∥平面PMB;
(2)证明:平面PMB⊥平面PAD;
(3)直线PB与平面PCD所成角的正弦值.
20.已知四棱锥P﹣ABCD(图1)的三视图如图2所示,△PBC为正三角形,PA垂直底面ABCD,俯视图是直角梯形.
(1)求正视图的面积;
(2)求四棱锥P﹣ABCD的体积;
(3)求证:AC⊥平面PAB.
21.已知函数f(x)=(log2x﹣2)(log4x﹣),2≤x≤4
(1)求该函数的值域;
(2)若f(x)≤mlog2x对于x∈[2,4]恒成立,求m的取值范围.
22.定义:若函数y=f(x)在某一区间D上任取两个实数x1、x2,且x1≠x2,都有,则称函数y=f(x)在区间D上具有性质L.
(1)写出一个在其定义域上具有性质L的对数函数(不要求证明).
(2)对于函数,判断其在区间(0,+∞)上是否具有性质L?并用所给定义证明你的结论.
(3)若函数在区间(0,1)上具有性质L,求实数a的取值范围.
2016-2017学年湖南省株洲市长鸿实验学校、南方中学、醴陵一中高一(上)12月联考数学试卷
参考答案与试题解析
一、单项选择题(本大题共12小题,每小题5分,共60分)
1.已知全集U={1,2,3,4,5},集合A={3,4},B={2,3,5},那么集合A∪( UB)等于( )
A.{1,2,3,4,5}
B.{3,4}
C.{1,3,4}
D.{2,3,4,5}
【考点】交、并、补集的混合运算.
【分析】由题意全集U={1,2,3,4,5},集合A={3,4},B={2,3,5},根据补集的定义可得C∪B={1,4},再根据并集的定义计算A∪(C∪B).
【解答】解:∵U={1,2,3,4,5},B={2,3,5},
∴C∪B={1,4},
∵集合A={3,4},
∴A∪(C∪B)={1,3,4},
故选C.
2.有下列命题:
①若直线l平行于平面α内的无数条直线,则直线l∥α:
②若直线a在平面α外.则a∥α:
③若直线a∥b,b∥α,则a∥α:
④若直线a∥b.b∥α.则a平行于平面α内的无数条直线.
其中真命题的个数是( )
A.1
B.2
C.3
D.4
【考点】空间中直线与平面之间的位置关系.
【分析】在①中,直线l与α相交、平行或l α:在②中,a与α平行或相交;在③中,a∥α或a α;在④中,a∥α或a α,故a平行于平面α内的无数条直线.
【解答】解:在①中,若直线l平行于平面α内的无数条直线,当这无数条直线不相交时,
则直线l与α相交、平行或l α,故①错误:
在②中,若直线a在平面α外.则a与α平行或相交,故②错误;
在③中,若直线a∥b,b∥a,则a∥α或a α,故③错误;
在④中,若直线a∥b.b∥a,则a∥α或a α,
∴a平行于平面α内的无数条直线,故④正确.
故选:A.
3.函数f(x)=+log2(x+1)的定义域为( )
A.[1,3)
B.(
1,3)
C.(﹣1,3]
D.[﹣1,3]
【考点】函数的定义域及其求法.
【分析】函数f(x)=+log2(x+1)有意义,只需3﹣x≥0,且x+1>0,解不等式即可得到所求定义域.
【解答】解:函数f(x)=+log2(x+1)有意义,
只需3﹣x≥0,且x+1>0,
解得﹣1<x≤3,
定义域为(﹣1,3].
故选:C.
4.某四棱锥的三视图如图所示,该四棱锥的表面积是( )
A.16
B.16+16
C.32
D.16+32
【考点】由三视图求面积、体积.
【分析】由已知中的三视力可得该几何体是一个四棱锥,求出各个面的面积,相加可得答案.
【解答】解:由已知中的三视力可得该几何体是一个四棱锥,
棱锥的底面边长为4,故底面面积为16,
棱锥的高为2,故侧面的高为:2,
则每个侧面的面积为:
=4,
故棱锥的表面积为:16+16,
故选:B
5.函数f(x)=2x+x﹣2的零点所在区间是( )
A.(﹣∞,﹣1)
B.(﹣l,0)
C.(0,1)
D.(1,2)
【考点】函数零点的判定定理.
【分析】据函数零点的判定定理,判断f(﹣1),f(0),f(1),f(2)的符号,即可求得结论.
【解答】解:f(﹣1)=2﹣1+1﹣2=﹣<0,
f(0)=﹣1<0,f(1)=1>0,f(2)=4>0,
故有f(0) f(1)<0,由零点的存在性定理可知:
函数f(x)=2x+x﹣2的零点所在的区间是(0,1)
故选:C.
6.如图,一个水平放置的平面图形的斜二测直观图是一个底角为45°,腰和上底均为1的等腰梯形,那么原平面图形的面积是( )
A.
B.
C.
D.
【考点】平面图形的直观图.
【分析】根据题意,画出图形,结合图形,得出原来的平面图形的上底与下底、高,从而求出它的面积.
【解答】解:根据题意,画出图形,如图所示;
则原来的平面图形上底是1,下底是1+,高是2,
∴它的面积是×(1+1+)×2=2+.
故选:D.
7.设二次函数f(x)=﹣x2+x+a(a<0),若f(m)>0,则f(m+1)的值为( )
A.正数
B.负数
C.非负数
D.正数、负数或零都有可能
【考点】二次函数的性质.
【分析】由f(x)=﹣x2+x+a(a<0),可知f(0)=(1)=a<0,再判断出0<m<1,从而解出问题.
【解答】解:∵f(x)=﹣x2+x+a(a<0),
∴f(0)=(1)=a<0,又∵f(m)>0,
则0<m<1,
则m+1>1,
则f(m+1)<f(1)<0,
故为负数,
故选B.
8.如图是正方体的侧面展开图,L1、L2是两条侧面对角线,则在正方体中,L1与L2( )
A.互相平行
B.相交
C.异面且互相垂直
D.异面且夹角为60°
【考点】空间中直线与直线之间的位置关系;异面直线及其所成的角.
【分析】以涂有红色的正方形为下底面,并且使l1所在侧面正对着我们,可得l1与l2是相交直线.
【解答】解:如图,以涂有红色的正方形为下底面,
并且使l1所在侧面正对着我们,
可得l2所在的面是上底面,且两条直线有一个公共点
∴在正方体中,l1与l2是相交直线.
故选:B.
9.已知f(x)=是(﹣,+∞)上的增函数,那么a的取值范围是( )
A.(,2)
B.(1,2]
C.[,2]
D.(1,2)
【考点】函数单调性的性质.
【分析】根据分段函数在(﹣,+∞)上是增函数,y1=ax﹣a,x>1必须是增函数,即a>1,(1,+∞)单调递增,那么y2=,其对称轴x=,在[,1]必须是单调递增.结合单调递增的性质,y1≥y2可得结论.
【解答】解:分段函数在(﹣,+∞)上是增函数,y1=ax﹣a,x>1必须是增函数,即a>1,(1,+∞)单调递增,
那么y2=,其对称轴x=,在[,1]必须是单调递增.
∴,解得:.
在(﹣,+∞)上是增函数,那么y1的最小值要大于y2的最大值,即1,
解得:a≤2
∴a的取值范围是[,2].
故选:C.
10.一高为H、满缸水量为V0的鱼缸的轴截面如图所示,其底部碰了一个小洞,满缸水从洞中流出,若鱼缸水深为h时水的体积为V,则函数的大致图象可能是( )
A.
B.
C.
D.
【考点】函数的图象.
【分析】水深h越大,水的体积v就越大,故函数v=f(h)是个增函数,一开始增长越来越快,后来增长越来越慢,图象是先凹后凸的.
【解答】解:由图得水深h越大,水的体积v就越大,故函数v=f(h)是个增函数.
据四个选项提供的信息,
当h∈[O,H],我们可将水“流出”设想成“流入”,
这样每当h增加一个单位增量△h时,
根据鱼缸形状可知,函数V的变化,开始其增量越来越大,但经过中截面后则增量越来越小,
故V关于h的函数图象是先凹后凸的,曲线上的点的切线斜率先是逐渐变大,后又逐渐变小,
故选B.
11.下列四个正方体图形中,A,B为正方体的两个顶点,M,N,P分别为其所在棱的中点,能得出AB∥平面MNP的图形的序号是( )
A.①、②
B.①、③
C.②、③
D.②、④
【考点】直线与平面平行的判定.
【分析】分别利用线面平行的判定定理,在平面MNP中能否寻找一条直线和AB平行即可.
【解答】解:在①中NP平行所在正方体的那个侧面的对角线,从而平行AB,所以AB∥平面MNP;
在③中设过点B且垂直于上底面的棱与上底面交点为C,
则由NP∥CB,MN∥AC可知平面MNP∥平行平面ABC,
即AB∥平面MNP.
故选B.
12.对于集合M、N,定义M﹣N={x|x∈M,且x N},M N=(M﹣N)∪(N﹣M).设A={y|y=x2﹣3x,x∈R},B={y|y=﹣2x,x∈R},则A B=( )
A.
B.
C.
D.
【考点】交、并、补集的混合运算.
【分析】由题设条件求出A=[﹣,+∞),B=(﹣∞,0),从而得到A﹣B=[0,+∞),B﹣A=,由此能求出A B.
【解答】解:∵A={y|y=x2﹣3x,x∈R}={x|y=(x﹣)2﹣}={y|y}=[﹣,+∞),
B={y|y=﹣2x,x∈R}={y|y<0}=(﹣∞,0),
∴A﹣B=[0,+∞),B﹣A=.
∴,
故选C.
二、填空题(本大题共4小题,每小题5分,共20分,将答案填在题中的横线上.)
13.f(x)=,若f(x)=1,则x= 2 .
【考点】函数的值.
【分析】当x<2时,f(x)=3x﹣2=1;当x≥2时,f(x)=.由此能求出结果.
【解答】解:∵f(x)=,f(x)=1,
∴当x<2时,f(x)=3x﹣2=1,解得x=2,不成立;
当x≥2时,f(x)=,解得x=2或x=﹣2(舍).
综上,x=2.
故答案为:2.
14.若三棱锥P﹣ABC的侧棱长PA=PB=PC,则点P在底面的射影O是△ABC的 外 心.
【考点】平行投影及平行投影作图法.
【分析】根据从一点出发的斜线段,如果斜线段长相等,那么它们的射影长也相等得到,点P在底面的射影O到三角形三个顶点的距离相等,从而即可选出答案.
【解答】解:如图,由题意得:
PA=PB=PC,
∴OA=OB=OC,
即O点是三角形ABC的外心,
故答案为外.
15.函数f(x)是定义在(0,+∞)上的增函数,且满足f(a b)=f(a)+f(b),f(3)=1则不等式:f(x)﹣f(x﹣2)>3的解集为 (2,) .
【考点】抽象函数及其应用.
【分析】由题意知f(2×2)=f(2)+f(2)=2,f(2×4)=f(2)+f(4)=3,f(x)>f(8x﹣16),再由f(x)的定义域为(0,+∞),且在其上为增函数得得到不等式组,即可解得答案.
【解答】解:∵f(xy)=f(x)+f(y),f(3)=1,
∴f(3×3)=f(3)+f(3)=2,
f(3×9)=f(3)+f(9)=3,
∵f(x)﹣f(x﹣2)>3,
∴f(x)>f(x﹣2)+f(27)=f(27x﹣54)
∵f(x)是定义在(0,+∞)上的增函数解得,
解得,2<x<.
所以不等式f(x)﹣f(x﹣2)<3的解集为(2,).
故答案为:(2,).
16.如图,半径为4的球O中有一内接圆柱,当圆柱的侧面积最大时,球的表面积与该圆柱的侧面积之差是 32π .
【考点】球内接多面体.
【分析】根据题意,结合图形,利用直角三角形的边角关系,求出内接圆柱的侧面积以及面积最大值,再求出S球﹣S圆柱侧的值.
【解答】解:如图所示,
设∠OAO′=θ,半径O′A=4cosθ=r,OO′=4sinθ;
∴S圆柱侧=2πr 2OO′
=2π 4cosθ 2 4sinθ
=64πsinθcosθ
=32πsin2θ,
∴当sin2θ=1,即θ=45°时,圆柱的侧面积取得最大值32π,
此时S球=4π×16=64π,
S球﹣S圆柱侧=32π.
故答案为:32π.
三、解答题(本大题共6小题,共70分,解答应写出文字说明.证明过程或演算步骤)
17.已知函数f(x)是定义在R上的奇函数,当x≥0时,f(x)=x2﹣2x.
(1)求f(x)的解析式,并画出的f(x)图象;
(2)设g(x)=f(x)﹣k,利用图象求:当实数k为何值时,函数g(x)有三个零点.
【考点】函数奇偶性的性质;函数解析式的求解及常用方法.
【分析】(1)设x<0,则﹣x>0,由条件求得f(x)的解析式,再根据奇函数的性质求出f(x)的解析式.
(2)由题意可得f(x)的图象和直线y=k有3个交点,数形结合求得k的范围.
【解答】解:(1)设x<0,则﹣x>0,由当x≥0时,f(x)=x2﹣2x,可得f(﹣x)=x2
+2x,
∵函数f(x)是定义在R上的奇函数,故有f(﹣x)=x2
+2x=﹣f(x),
∴f(x)=﹣x2
﹣2x,∴f(x)=.
(2)g(x)=f(x)﹣k有三个零点,即f(x)的图象和直线y=k有3个交点.
由于函数f(x)的极大值为f(﹣1)=1,极小值
f(1)=﹣1,如图:
故﹣1<k<1.
18.设全集为U=R,集合A={x|(x+3)(4﹣x)≤0},B={x|log2(x+2)<3}.
(1)求A∩ UB;
(2)已知C={x|2a<x<a+1},若C A∪B,求实数a的取值范围.
【考点】集合的包含关系判断及应用;交、并、补集的混合运算.
【分析】(1)由题目所给的条件,可以分别解出集合A与集合B,由补集的知识,可得 UB,即可求得A∩ UB;
(2)求出A∪B,通过分类讨论,对a进行分类,可以确定C是否为空集,进而可以讨论的a的取值范围.
【解答】解:(1)集合A={x|(x+3)(4﹣x)≤0}={x|x≤﹣3或x≥4},….
对于集合B={x|log2(x+2)<3}.,有x+2>0且x+2<8,即﹣2<x<6,….
即B=(﹣2,6),∴CUB=(﹣∞,﹣2]∪[6,+∞),
所以A∩ UB=(﹣∞,﹣3]∪[6,+∞).…
(2)因为A∪B=(﹣∞,﹣3]∪[﹣2,+∞).…
①当2a≥a+!,即a≥1时,C= ,满足题意.…
②当2a<a+1,即a<1时,有a+1≤﹣3或2a≥﹣2,
即a≤﹣4或﹣1≤a<1.
综上,实数a的取值范围为(﹣∞,﹣4]∪[﹣1,+∞).…
19.已知四棱锥P﹣ABCD,底面ABCD是∠A=60°、边长为a的菱形,又PD⊥底面
ABCD,且PD=CD,点M、N分别是棱AD、PC的中点.
(1)证明:DN∥平面PMB;
(2)证明:平面PMB⊥平面PAD;
(3)直线PB与平面PCD所成角的正弦值.
【考点】直线与平面所成的角;直线与平面平行的判定;平面与平面垂直的判定.
【分析】(1)取PB中点Q,连结MQ、NQ,利用三角形中位线定理和菱形的性质,证出DN∥MQ.利用线面平行判定定理,即可证出DN∥平面PMB;
(2)由菱形ABCD中∠A=60°,得到△ABD是正三角形,从而MB⊥AD.由PD⊥底ABCD得到PD⊥MB,利用线面垂直的判定定理,证出MB⊥平面PAD,结合面面垂直判定定理可得平面PMB⊥平面PAD;
(3)证明△BCD为等边三角形,设CD中点为E,连接PE,DE,可得∠PBE为直线PB与平面PCD所成角.
【解答】(1)证明:取PB中点Q,连结MQ、NQ,
因为M、N分别是棱AD、PC中点,
所以QN∥BC∥MD,且QN=MD,于是DN∥MQ.
∵MQ 平面PMB,DN 平面PMB
∴DN∥平面PMB;…
(2)证明:∵PD⊥底ABCD,MB 平面ABCD,
∴PD⊥MB
又∵底面ABCD为菱形,∠A=60°且M为AD中点,
∴MB⊥AD.
又∵AD、PD是平面PAD内的相交直线,∴MB⊥平面PAD.
∵MB 平面PMB,∴平面PMB⊥平面PAD;
…
(3)解:设CD中点为E,连接PE,DE,
∵底面ABCD是∠A=60°、边长为a
的菱形
∴△BCD是等边三角形,
∴BE⊥DC,
∵PD⊥底面
ABCD,
∴PD⊥BE,
∴BE⊥平面PCD,
∴∠PBE为直线PB与平面PCD所成角,
∵BE=a,PA=,
∴sin∠BPE=…
20.已知四棱锥P﹣ABCD(图1)的三视图如图2所示,△PBC为正三角形,PA垂直底面ABCD,俯视图是直角梯形.
(1)求正视图的面积;
(2)求四棱锥P﹣ABCD的体积;
(3)求证:AC⊥平面PAB.
【考点】直线与平面垂直的判定;由三视图求面积、体积;棱柱、棱锥、棱台的体积.
【分析】(1)过A作AE∥CD,可得E是BC的中点,且BE=CE=AE=CD=1.正三角形PBC中,算出中线PE=,由PA⊥平面ABCD,在Rt△PAE中,算出PA=即为正视图三角形的高长,由此结合BC=2即可求出正视图的面积;
(2)由(1)的证明,结合题意可得四棱锥P﹣ABCD是以PA为高、底面ABCD是直角梯形的四棱锥,结合题中的数据即可算出四棱锥P﹣ABCD的体积;
(3)分别在Rt△ABE、Rt△ADC中,算出AB=AC=,结合BC=2利用勾股定理的逆定理证出AC⊥AB,再由PA⊥平面ABCD得PA⊥AC,根据线面垂直的判定定理即可证出AC⊥平面PAB.
【解答】解:(1)过A作AE∥CD,根据三视图可知,E是BC的中点,(1
分)
且BE=CE=1,AE=CD=1(2
分)
又∵△PBC为正三角形,∴BC=PB=PC=2,且PE⊥BC
∴PE2=PC2﹣CE2=3(3
分)
∵PA⊥平面ABCD,AE 平面ABCD,∴PA⊥AE(4
分)
可得PA2=PE2﹣AE2=2,即(5
分)
因此,正视图的面积为(6
分)
(2)由(1)可知,四棱锥P﹣ABCD的高为PA,,(7
分)
底面积为
∴四棱锥P﹣ABCD的体积为(10
分)
(3)∵PA⊥平面ABCD,AC 平面ABCD,∴PA⊥AC(11
分)
∵在Rt△ABE中,AB2=AE2+BE2=2,在Rt△ADC中,AC2=AD2+CD2=2(12
分)
∴BC2=4=AB2+AC2,可得△BAC是直角三角形
(13
分)
∴AC⊥AB.
由此结合AB∩PA=A,可得AC⊥平面PAB(14
分)
21.已知函数f(x)=(log2x﹣2)(log4x﹣),2≤x≤4
(1)求该函数的值域;
(2)若f(x)≤mlog2x对于x∈[2,4]恒成立,求m的取值范围.
【考点】函数恒成立问题;函数的值域;二次函数的性质;二次函数在闭区间上的最值.
【分析】(1)f(x)=(log2x﹣2)(log4x﹣)=,2≤x≤4令t=log2x,则y==,由此能求出函数的值域.
(2)令t=log2x,得对于1≤t≤2恒成立,从而得到m≥对于t∈[1,2]恒成立,构造函数g(t)=,t∈[1,2],能求出m的取值范围.
【解答】解:(1)f(x)=(log2x﹣2)(log4x﹣)
=,2≤x≤4
令t=log2x,则y==,
∵2≤x≤4,∴1≤t≤2.
当t=时,ymin=﹣,当t=1,或t=2时,ymax=0.
∴函数的值域是[﹣].
(2)令t=log2x,得对于1≤t≤2恒成立.
∴m≥对于t∈[1,2]恒成立,
设g(t)=,t∈[1,2],
∴g(t)==,
∵g(1)=0,g(2)=0,
∴g(t)max=0,∴m≥0.
故m的取值范围是[0,+∞).
22.定义:若函数y=f(x)在某一区间D上任取两个实数x1、x2,且x1≠x2,都有,则称函数y=f(x)在区间D上具有性质L.
(1)写出一个在其定义域上具有性质L的对数函数(不要求证明).
(2)对于函数,判断其在区间(0,+∞)上是否具有性质L?并用所给定义证明你的结论.
(3)若函数在区间(0,1)上具有性质L,求实数a的取值范围.
【考点】函数与方程的综合运用.
【分析】(1)写出的函数是下凹的函数即可;
(2)函数在区间(0,+∞)上具有性质L.根据定义,任取x1、x2∈(0,+∞),且x1≠x2
只需要证明>0即可;
(3)任取x1、x2∈(0,1),且x1≠x2则>0,只需要2﹣a x1 x2(x1+x2)>0在x1、x2∈(0,1)上恒成立,即,故可求实数a的取值范围.
【解答】解:(1)(或其它底在(0,1)上的对数函数).…
(2)函数在区间(0,+∞)上具有性质L.…
证明:任取x1、x2∈(0,+∞),且x1≠x2
则==
∵x1、x2∈(0,+∞)且x1≠x2,
∴(x1﹣x2)2>0,2x1 x2(x1+x2)>0
即>0,
∴
所以函数在区间(0,+∞)上具有性质L.…
(3)任取x1、x2∈(0,1),且x1≠x2
则===
∵x1、x2∈(0,1)且x1≠x2,
∴(x1﹣x2)2>0,4x1 x2(x1+x2)>0
要使上式大于零,必须2﹣a x1 x2(x1+x2)>0在x1、x2∈(0,1)上恒成立,
即,
∴a≤1,
即实数a的取值范围为(﹣∞,1]…
2017年1月20日
一、单项选择题(本大题共12小题,每小题5分,共60分)
1.已知全集U={1,2,3,4,5},集合A={3,4},B={2,3,5},那么集合A∪( UB)等于( )
A.{1,2,3,4,5}
B.{3,4}
C.{1,3,4}
D.{2,3,4,5}
2.有下列命题:
①若直线l平行于平面α内的无数条直线,则直线l∥α:
②若直线a在平面α外.则a∥α:
③若直线a∥b,b∥α,则a∥α:
④若直线a∥b.b∥α.则a平行于平面α内的无数条直线.
其中真命题的个数是( )
A.1
B.2
C.3
D.4
3.函数f(x)=+log2(x+1)的定义域为( )
A.[1,3)
B.(
1,3)
C.(﹣1,3]
D.[﹣1,3]
4.某四棱锥的三视图如图所示,该四棱锥的表面积是( )
A.16
B.16+16
C.32
D.16+32
5.函数f(x)=2x+x﹣2的零点所在区间是( )
A.(﹣∞,﹣1)
B.(﹣l,0)
C.(0,1)
D.(1,2)
6.如图,一个水平放置的平面图形的斜二测直观图是一个底角为45°,腰和上底均为1的等腰梯形,那么原平面图形的面积是( )
A.
B.
C.
D.
7.设二次函数f(x)=﹣x2+x+a(a<0),若f(m)>0,则f(m+1)的值为( )
A.正数
B.负数
C.非负数
D.正数、负数或零都有可能
8.如图是正方体的侧面展开图,L1、L2是两条侧面对角线,则在正方体中,L1与L2( )
A.互相平行
B.相交
C.异面且互相垂直
D.异面且夹角为60°
9.已知f(x)=是(﹣,+∞)上的增函数,那么a的取值范围是( )
A.(,2)
B.(1,2]
C.[,2]
D.(1,2)
10.一高为H、满缸水量为V0的鱼缸的轴截面如图所示,其底部碰了一个小洞,满缸水从洞中流出,若鱼缸水深为h时水的体积为V,则函数的大致图象可能是( )
A.
B.
C.
D.
11.下列四个正方体图形中,A,B为正方体的两个顶点,M,N,P分别为其所在棱的中点,能得出AB∥平面MNP的图形的序号是( )
A.①、②
B.①、③
C.②、③
D.②、④
12.对于集合M、N,定义M﹣N={x|x∈M,且x N},M N=(M﹣N)∪(N﹣M).设A={y|y=x2﹣3x,x∈R},B={y|y=﹣2x,x∈R},则A B=( )
A.
B.
C.
D.
二、填空题(本大题共4小题,每小题5分,共20分,将答案填在题中的横线上.)
13.f(x)=,若f(x)=1,则x= .
14.若三棱锥P﹣ABC的侧棱长PA=PB=PC,则点P在底面的射影O是△ABC的 心.
15.函数f(x)是定义在(0,+∞)上的增函数,且满足f(a b)=f(a)+f(b),f(3)=1则不等式:f(x)﹣f(x﹣2)>3的解集为 .
16.如图,半径为4的球O中有一内接圆柱,当圆柱的侧面积最大时,球的表面积与该圆柱的侧面积之差是 .
三、解答题(本大题共6小题,共70分,解答应写出文字说明.证明过程或演算步骤)
17.已知函数f(x)是定义在R上的奇函数,当x≥0时,f(x)=x2﹣2x.
(1)求f(x)的解析式,并画出的f(x)图象;
(2)设g(x)=f(x)﹣k,利用图象求:当实数k为何值时,函数g(x)有三个零点.
18.设全集为U=R,集合A={x|(x+3)(4﹣x)≤0},B={x|log2(x+2)<3}.
(1)求A∩ UB;
(2)已知C={x|2a<x<a+1},若C A∪B,求实数a的取值范围.
19.已知四棱锥P﹣ABCD,底面ABCD是∠A=60°、边长为a的菱形,又PD⊥底面
ABCD,且PD=CD,点M、N分别是棱AD、PC的中点.
(1)证明:DN∥平面PMB;
(2)证明:平面PMB⊥平面PAD;
(3)直线PB与平面PCD所成角的正弦值.
20.已知四棱锥P﹣ABCD(图1)的三视图如图2所示,△PBC为正三角形,PA垂直底面ABCD,俯视图是直角梯形.
(1)求正视图的面积;
(2)求四棱锥P﹣ABCD的体积;
(3)求证:AC⊥平面PAB.
21.已知函数f(x)=(log2x﹣2)(log4x﹣),2≤x≤4
(1)求该函数的值域;
(2)若f(x)≤mlog2x对于x∈[2,4]恒成立,求m的取值范围.
22.定义:若函数y=f(x)在某一区间D上任取两个实数x1、x2,且x1≠x2,都有,则称函数y=f(x)在区间D上具有性质L.
(1)写出一个在其定义域上具有性质L的对数函数(不要求证明).
(2)对于函数,判断其在区间(0,+∞)上是否具有性质L?并用所给定义证明你的结论.
(3)若函数在区间(0,1)上具有性质L,求实数a的取值范围.
2016-2017学年湖南省株洲市长鸿实验学校、南方中学、醴陵一中高一(上)12月联考数学试卷
参考答案与试题解析
一、单项选择题(本大题共12小题,每小题5分,共60分)
1.已知全集U={1,2,3,4,5},集合A={3,4},B={2,3,5},那么集合A∪( UB)等于( )
A.{1,2,3,4,5}
B.{3,4}
C.{1,3,4}
D.{2,3,4,5}
【考点】交、并、补集的混合运算.
【分析】由题意全集U={1,2,3,4,5},集合A={3,4},B={2,3,5},根据补集的定义可得C∪B={1,4},再根据并集的定义计算A∪(C∪B).
【解答】解:∵U={1,2,3,4,5},B={2,3,5},
∴C∪B={1,4},
∵集合A={3,4},
∴A∪(C∪B)={1,3,4},
故选C.
2.有下列命题:
①若直线l平行于平面α内的无数条直线,则直线l∥α:
②若直线a在平面α外.则a∥α:
③若直线a∥b,b∥α,则a∥α:
④若直线a∥b.b∥α.则a平行于平面α内的无数条直线.
其中真命题的个数是( )
A.1
B.2
C.3
D.4
【考点】空间中直线与平面之间的位置关系.
【分析】在①中,直线l与α相交、平行或l α:在②中,a与α平行或相交;在③中,a∥α或a α;在④中,a∥α或a α,故a平行于平面α内的无数条直线.
【解答】解:在①中,若直线l平行于平面α内的无数条直线,当这无数条直线不相交时,
则直线l与α相交、平行或l α,故①错误:
在②中,若直线a在平面α外.则a与α平行或相交,故②错误;
在③中,若直线a∥b,b∥a,则a∥α或a α,故③错误;
在④中,若直线a∥b.b∥a,则a∥α或a α,
∴a平行于平面α内的无数条直线,故④正确.
故选:A.
3.函数f(x)=+log2(x+1)的定义域为( )
A.[1,3)
B.(
1,3)
C.(﹣1,3]
D.[﹣1,3]
【考点】函数的定义域及其求法.
【分析】函数f(x)=+log2(x+1)有意义,只需3﹣x≥0,且x+1>0,解不等式即可得到所求定义域.
【解答】解:函数f(x)=+log2(x+1)有意义,
只需3﹣x≥0,且x+1>0,
解得﹣1<x≤3,
定义域为(﹣1,3].
故选:C.
4.某四棱锥的三视图如图所示,该四棱锥的表面积是( )
A.16
B.16+16
C.32
D.16+32
【考点】由三视图求面积、体积.
【分析】由已知中的三视力可得该几何体是一个四棱锥,求出各个面的面积,相加可得答案.
【解答】解:由已知中的三视力可得该几何体是一个四棱锥,
棱锥的底面边长为4,故底面面积为16,
棱锥的高为2,故侧面的高为:2,
则每个侧面的面积为:
=4,
故棱锥的表面积为:16+16,
故选:B
5.函数f(x)=2x+x﹣2的零点所在区间是( )
A.(﹣∞,﹣1)
B.(﹣l,0)
C.(0,1)
D.(1,2)
【考点】函数零点的判定定理.
【分析】据函数零点的判定定理,判断f(﹣1),f(0),f(1),f(2)的符号,即可求得结论.
【解答】解:f(﹣1)=2﹣1+1﹣2=﹣<0,
f(0)=﹣1<0,f(1)=1>0,f(2)=4>0,
故有f(0) f(1)<0,由零点的存在性定理可知:
函数f(x)=2x+x﹣2的零点所在的区间是(0,1)
故选:C.
6.如图,一个水平放置的平面图形的斜二测直观图是一个底角为45°,腰和上底均为1的等腰梯形,那么原平面图形的面积是( )
A.
B.
C.
D.
【考点】平面图形的直观图.
【分析】根据题意,画出图形,结合图形,得出原来的平面图形的上底与下底、高,从而求出它的面积.
【解答】解:根据题意,画出图形,如图所示;
则原来的平面图形上底是1,下底是1+,高是2,
∴它的面积是×(1+1+)×2=2+.
故选:D.
7.设二次函数f(x)=﹣x2+x+a(a<0),若f(m)>0,则f(m+1)的值为( )
A.正数
B.负数
C.非负数
D.正数、负数或零都有可能
【考点】二次函数的性质.
【分析】由f(x)=﹣x2+x+a(a<0),可知f(0)=(1)=a<0,再判断出0<m<1,从而解出问题.
【解答】解:∵f(x)=﹣x2+x+a(a<0),
∴f(0)=(1)=a<0,又∵f(m)>0,
则0<m<1,
则m+1>1,
则f(m+1)<f(1)<0,
故为负数,
故选B.
8.如图是正方体的侧面展开图,L1、L2是两条侧面对角线,则在正方体中,L1与L2( )
A.互相平行
B.相交
C.异面且互相垂直
D.异面且夹角为60°
【考点】空间中直线与直线之间的位置关系;异面直线及其所成的角.
【分析】以涂有红色的正方形为下底面,并且使l1所在侧面正对着我们,可得l1与l2是相交直线.
【解答】解:如图,以涂有红色的正方形为下底面,
并且使l1所在侧面正对着我们,
可得l2所在的面是上底面,且两条直线有一个公共点
∴在正方体中,l1与l2是相交直线.
故选:B.
9.已知f(x)=是(﹣,+∞)上的增函数,那么a的取值范围是( )
A.(,2)
B.(1,2]
C.[,2]
D.(1,2)
【考点】函数单调性的性质.
【分析】根据分段函数在(﹣,+∞)上是增函数,y1=ax﹣a,x>1必须是增函数,即a>1,(1,+∞)单调递增,那么y2=,其对称轴x=,在[,1]必须是单调递增.结合单调递增的性质,y1≥y2可得结论.
【解答】解:分段函数在(﹣,+∞)上是增函数,y1=ax﹣a,x>1必须是增函数,即a>1,(1,+∞)单调递增,
那么y2=,其对称轴x=,在[,1]必须是单调递增.
∴,解得:.
在(﹣,+∞)上是增函数,那么y1的最小值要大于y2的最大值,即1,
解得:a≤2
∴a的取值范围是[,2].
故选:C.
10.一高为H、满缸水量为V0的鱼缸的轴截面如图所示,其底部碰了一个小洞,满缸水从洞中流出,若鱼缸水深为h时水的体积为V,则函数的大致图象可能是( )
A.
B.
C.
D.
【考点】函数的图象.
【分析】水深h越大,水的体积v就越大,故函数v=f(h)是个增函数,一开始增长越来越快,后来增长越来越慢,图象是先凹后凸的.
【解答】解:由图得水深h越大,水的体积v就越大,故函数v=f(h)是个增函数.
据四个选项提供的信息,
当h∈[O,H],我们可将水“流出”设想成“流入”,
这样每当h增加一个单位增量△h时,
根据鱼缸形状可知,函数V的变化,开始其增量越来越大,但经过中截面后则增量越来越小,
故V关于h的函数图象是先凹后凸的,曲线上的点的切线斜率先是逐渐变大,后又逐渐变小,
故选B.
11.下列四个正方体图形中,A,B为正方体的两个顶点,M,N,P分别为其所在棱的中点,能得出AB∥平面MNP的图形的序号是( )
A.①、②
B.①、③
C.②、③
D.②、④
【考点】直线与平面平行的判定.
【分析】分别利用线面平行的判定定理,在平面MNP中能否寻找一条直线和AB平行即可.
【解答】解:在①中NP平行所在正方体的那个侧面的对角线,从而平行AB,所以AB∥平面MNP;
在③中设过点B且垂直于上底面的棱与上底面交点为C,
则由NP∥CB,MN∥AC可知平面MNP∥平行平面ABC,
即AB∥平面MNP.
故选B.
12.对于集合M、N,定义M﹣N={x|x∈M,且x N},M N=(M﹣N)∪(N﹣M).设A={y|y=x2﹣3x,x∈R},B={y|y=﹣2x,x∈R},则A B=( )
A.
B.
C.
D.
【考点】交、并、补集的混合运算.
【分析】由题设条件求出A=[﹣,+∞),B=(﹣∞,0),从而得到A﹣B=[0,+∞),B﹣A=,由此能求出A B.
【解答】解:∵A={y|y=x2﹣3x,x∈R}={x|y=(x﹣)2﹣}={y|y}=[﹣,+∞),
B={y|y=﹣2x,x∈R}={y|y<0}=(﹣∞,0),
∴A﹣B=[0,+∞),B﹣A=.
∴,
故选C.
二、填空题(本大题共4小题,每小题5分,共20分,将答案填在题中的横线上.)
13.f(x)=,若f(x)=1,则x= 2 .
【考点】函数的值.
【分析】当x<2时,f(x)=3x﹣2=1;当x≥2时,f(x)=.由此能求出结果.
【解答】解:∵f(x)=,f(x)=1,
∴当x<2时,f(x)=3x﹣2=1,解得x=2,不成立;
当x≥2时,f(x)=,解得x=2或x=﹣2(舍).
综上,x=2.
故答案为:2.
14.若三棱锥P﹣ABC的侧棱长PA=PB=PC,则点P在底面的射影O是△ABC的 外 心.
【考点】平行投影及平行投影作图法.
【分析】根据从一点出发的斜线段,如果斜线段长相等,那么它们的射影长也相等得到,点P在底面的射影O到三角形三个顶点的距离相等,从而即可选出答案.
【解答】解:如图,由题意得:
PA=PB=PC,
∴OA=OB=OC,
即O点是三角形ABC的外心,
故答案为外.
15.函数f(x)是定义在(0,+∞)上的增函数,且满足f(a b)=f(a)+f(b),f(3)=1则不等式:f(x)﹣f(x﹣2)>3的解集为 (2,) .
【考点】抽象函数及其应用.
【分析】由题意知f(2×2)=f(2)+f(2)=2,f(2×4)=f(2)+f(4)=3,f(x)>f(8x﹣16),再由f(x)的定义域为(0,+∞),且在其上为增函数得得到不等式组,即可解得答案.
【解答】解:∵f(xy)=f(x)+f(y),f(3)=1,
∴f(3×3)=f(3)+f(3)=2,
f(3×9)=f(3)+f(9)=3,
∵f(x)﹣f(x﹣2)>3,
∴f(x)>f(x﹣2)+f(27)=f(27x﹣54)
∵f(x)是定义在(0,+∞)上的增函数解得,
解得,2<x<.
所以不等式f(x)﹣f(x﹣2)<3的解集为(2,).
故答案为:(2,).
16.如图,半径为4的球O中有一内接圆柱,当圆柱的侧面积最大时,球的表面积与该圆柱的侧面积之差是 32π .
【考点】球内接多面体.
【分析】根据题意,结合图形,利用直角三角形的边角关系,求出内接圆柱的侧面积以及面积最大值,再求出S球﹣S圆柱侧的值.
【解答】解:如图所示,
设∠OAO′=θ,半径O′A=4cosθ=r,OO′=4sinθ;
∴S圆柱侧=2πr 2OO′
=2π 4cosθ 2 4sinθ
=64πsinθcosθ
=32πsin2θ,
∴当sin2θ=1,即θ=45°时,圆柱的侧面积取得最大值32π,
此时S球=4π×16=64π,
S球﹣S圆柱侧=32π.
故答案为:32π.
三、解答题(本大题共6小题,共70分,解答应写出文字说明.证明过程或演算步骤)
17.已知函数f(x)是定义在R上的奇函数,当x≥0时,f(x)=x2﹣2x.
(1)求f(x)的解析式,并画出的f(x)图象;
(2)设g(x)=f(x)﹣k,利用图象求:当实数k为何值时,函数g(x)有三个零点.
【考点】函数奇偶性的性质;函数解析式的求解及常用方法.
【分析】(1)设x<0,则﹣x>0,由条件求得f(x)的解析式,再根据奇函数的性质求出f(x)的解析式.
(2)由题意可得f(x)的图象和直线y=k有3个交点,数形结合求得k的范围.
【解答】解:(1)设x<0,则﹣x>0,由当x≥0时,f(x)=x2﹣2x,可得f(﹣x)=x2
+2x,
∵函数f(x)是定义在R上的奇函数,故有f(﹣x)=x2
+2x=﹣f(x),
∴f(x)=﹣x2
﹣2x,∴f(x)=.
(2)g(x)=f(x)﹣k有三个零点,即f(x)的图象和直线y=k有3个交点.
由于函数f(x)的极大值为f(﹣1)=1,极小值
f(1)=﹣1,如图:
故﹣1<k<1.
18.设全集为U=R,集合A={x|(x+3)(4﹣x)≤0},B={x|log2(x+2)<3}.
(1)求A∩ UB;
(2)已知C={x|2a<x<a+1},若C A∪B,求实数a的取值范围.
【考点】集合的包含关系判断及应用;交、并、补集的混合运算.
【分析】(1)由题目所给的条件,可以分别解出集合A与集合B,由补集的知识,可得 UB,即可求得A∩ UB;
(2)求出A∪B,通过分类讨论,对a进行分类,可以确定C是否为空集,进而可以讨论的a的取值范围.
【解答】解:(1)集合A={x|(x+3)(4﹣x)≤0}={x|x≤﹣3或x≥4},….
对于集合B={x|log2(x+2)<3}.,有x+2>0且x+2<8,即﹣2<x<6,….
即B=(﹣2,6),∴CUB=(﹣∞,﹣2]∪[6,+∞),
所以A∩ UB=(﹣∞,﹣3]∪[6,+∞).…
(2)因为A∪B=(﹣∞,﹣3]∪[﹣2,+∞).…
①当2a≥a+!,即a≥1时,C= ,满足题意.…
②当2a<a+1,即a<1时,有a+1≤﹣3或2a≥﹣2,
即a≤﹣4或﹣1≤a<1.
综上,实数a的取值范围为(﹣∞,﹣4]∪[﹣1,+∞).…
19.已知四棱锥P﹣ABCD,底面ABCD是∠A=60°、边长为a的菱形,又PD⊥底面
ABCD,且PD=CD,点M、N分别是棱AD、PC的中点.
(1)证明:DN∥平面PMB;
(2)证明:平面PMB⊥平面PAD;
(3)直线PB与平面PCD所成角的正弦值.
【考点】直线与平面所成的角;直线与平面平行的判定;平面与平面垂直的判定.
【分析】(1)取PB中点Q,连结MQ、NQ,利用三角形中位线定理和菱形的性质,证出DN∥MQ.利用线面平行判定定理,即可证出DN∥平面PMB;
(2)由菱形ABCD中∠A=60°,得到△ABD是正三角形,从而MB⊥AD.由PD⊥底ABCD得到PD⊥MB,利用线面垂直的判定定理,证出MB⊥平面PAD,结合面面垂直判定定理可得平面PMB⊥平面PAD;
(3)证明△BCD为等边三角形,设CD中点为E,连接PE,DE,可得∠PBE为直线PB与平面PCD所成角.
【解答】(1)证明:取PB中点Q,连结MQ、NQ,
因为M、N分别是棱AD、PC中点,
所以QN∥BC∥MD,且QN=MD,于是DN∥MQ.
∵MQ 平面PMB,DN 平面PMB
∴DN∥平面PMB;…
(2)证明:∵PD⊥底ABCD,MB 平面ABCD,
∴PD⊥MB
又∵底面ABCD为菱形,∠A=60°且M为AD中点,
∴MB⊥AD.
又∵AD、PD是平面PAD内的相交直线,∴MB⊥平面PAD.
∵MB 平面PMB,∴平面PMB⊥平面PAD;
…
(3)解:设CD中点为E,连接PE,DE,
∵底面ABCD是∠A=60°、边长为a
的菱形
∴△BCD是等边三角形,
∴BE⊥DC,
∵PD⊥底面
ABCD,
∴PD⊥BE,
∴BE⊥平面PCD,
∴∠PBE为直线PB与平面PCD所成角,
∵BE=a,PA=,
∴sin∠BPE=…
20.已知四棱锥P﹣ABCD(图1)的三视图如图2所示,△PBC为正三角形,PA垂直底面ABCD,俯视图是直角梯形.
(1)求正视图的面积;
(2)求四棱锥P﹣ABCD的体积;
(3)求证:AC⊥平面PAB.
【考点】直线与平面垂直的判定;由三视图求面积、体积;棱柱、棱锥、棱台的体积.
【分析】(1)过A作AE∥CD,可得E是BC的中点,且BE=CE=AE=CD=1.正三角形PBC中,算出中线PE=,由PA⊥平面ABCD,在Rt△PAE中,算出PA=即为正视图三角形的高长,由此结合BC=2即可求出正视图的面积;
(2)由(1)的证明,结合题意可得四棱锥P﹣ABCD是以PA为高、底面ABCD是直角梯形的四棱锥,结合题中的数据即可算出四棱锥P﹣ABCD的体积;
(3)分别在Rt△ABE、Rt△ADC中,算出AB=AC=,结合BC=2利用勾股定理的逆定理证出AC⊥AB,再由PA⊥平面ABCD得PA⊥AC,根据线面垂直的判定定理即可证出AC⊥平面PAB.
【解答】解:(1)过A作AE∥CD,根据三视图可知,E是BC的中点,(1
分)
且BE=CE=1,AE=CD=1(2
分)
又∵△PBC为正三角形,∴BC=PB=PC=2,且PE⊥BC
∴PE2=PC2﹣CE2=3(3
分)
∵PA⊥平面ABCD,AE 平面ABCD,∴PA⊥AE(4
分)
可得PA2=PE2﹣AE2=2,即(5
分)
因此,正视图的面积为(6
分)
(2)由(1)可知,四棱锥P﹣ABCD的高为PA,,(7
分)
底面积为
∴四棱锥P﹣ABCD的体积为(10
分)
(3)∵PA⊥平面ABCD,AC 平面ABCD,∴PA⊥AC(11
分)
∵在Rt△ABE中,AB2=AE2+BE2=2,在Rt△ADC中,AC2=AD2+CD2=2(12
分)
∴BC2=4=AB2+AC2,可得△BAC是直角三角形
(13
分)
∴AC⊥AB.
由此结合AB∩PA=A,可得AC⊥平面PAB(14
分)
21.已知函数f(x)=(log2x﹣2)(log4x﹣),2≤x≤4
(1)求该函数的值域;
(2)若f(x)≤mlog2x对于x∈[2,4]恒成立,求m的取值范围.
【考点】函数恒成立问题;函数的值域;二次函数的性质;二次函数在闭区间上的最值.
【分析】(1)f(x)=(log2x﹣2)(log4x﹣)=,2≤x≤4令t=log2x,则y==,由此能求出函数的值域.
(2)令t=log2x,得对于1≤t≤2恒成立,从而得到m≥对于t∈[1,2]恒成立,构造函数g(t)=,t∈[1,2],能求出m的取值范围.
【解答】解:(1)f(x)=(log2x﹣2)(log4x﹣)
=,2≤x≤4
令t=log2x,则y==,
∵2≤x≤4,∴1≤t≤2.
当t=时,ymin=﹣,当t=1,或t=2时,ymax=0.
∴函数的值域是[﹣].
(2)令t=log2x,得对于1≤t≤2恒成立.
∴m≥对于t∈[1,2]恒成立,
设g(t)=,t∈[1,2],
∴g(t)==,
∵g(1)=0,g(2)=0,
∴g(t)max=0,∴m≥0.
故m的取值范围是[0,+∞).
22.定义:若函数y=f(x)在某一区间D上任取两个实数x1、x2,且x1≠x2,都有,则称函数y=f(x)在区间D上具有性质L.
(1)写出一个在其定义域上具有性质L的对数函数(不要求证明).
(2)对于函数,判断其在区间(0,+∞)上是否具有性质L?并用所给定义证明你的结论.
(3)若函数在区间(0,1)上具有性质L,求实数a的取值范围.
【考点】函数与方程的综合运用.
【分析】(1)写出的函数是下凹的函数即可;
(2)函数在区间(0,+∞)上具有性质L.根据定义,任取x1、x2∈(0,+∞),且x1≠x2
只需要证明>0即可;
(3)任取x1、x2∈(0,1),且x1≠x2则>0,只需要2﹣a x1 x2(x1+x2)>0在x1、x2∈(0,1)上恒成立,即,故可求实数a的取值范围.
【解答】解:(1)(或其它底在(0,1)上的对数函数).…
(2)函数在区间(0,+∞)上具有性质L.…
证明:任取x1、x2∈(0,+∞),且x1≠x2
则==
∵x1、x2∈(0,+∞)且x1≠x2,
∴(x1﹣x2)2>0,2x1 x2(x1+x2)>0
即>0,
∴
所以函数在区间(0,+∞)上具有性质L.…
(3)任取x1、x2∈(0,1),且x1≠x2
则===
∵x1、x2∈(0,1)且x1≠x2,
∴(x1﹣x2)2>0,4x1 x2(x1+x2)>0
要使上式大于零,必须2﹣a x1 x2(x1+x2)>0在x1、x2∈(0,1)上恒成立,
即,
∴a≤1,
即实数a的取值范围为(﹣∞,1]…
2017年1月20日
同课章节目录
