2.2轴对称的基本性质（第2课时）课件

课件23张PPT。2.2 轴对称的基本性质
第2课时1.探索利用坐标来表示轴对称；
2.掌握关于x轴、y轴对称的点的坐标特点.已知点A和一条直线MN，你能画出这个点关于已知直线
的对称点吗?AA′MN∴ A′就是点A关于直线MN的对称点.O然后延长AO至A′,使AO=OA′.过点A作AO⊥MN于O,·OA (2,3)你能说出点A与点A′坐标的关系吗？如图，在平面直角坐标
系中,你能画出点A关于
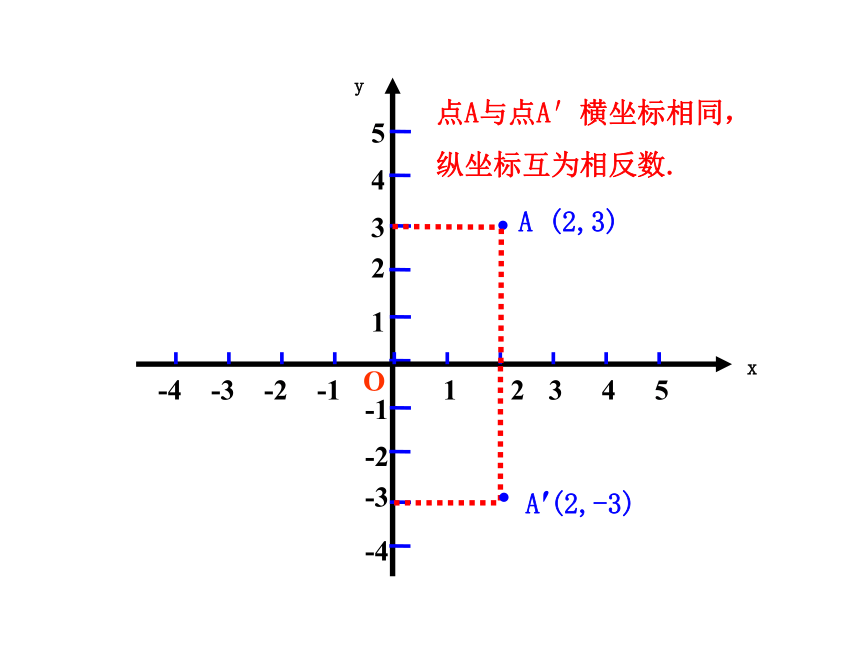
x轴的对称点吗?yx·12345-4-3-2-1A (2,3)·A′(2,-3)点A与点A′横坐标相同，
纵坐标互为相反数.xyOB (-4, 2)··C(3, -4)关于x轴
对称的点
的坐标具
有怎样的
关系？在平面直角坐标系中画出下列各点
关于x轴的对称点.yxOB (-4, 2)··C(3, -4)·B′ (-4, -2)·C′(3, 4)关于x轴对称的点的横坐标
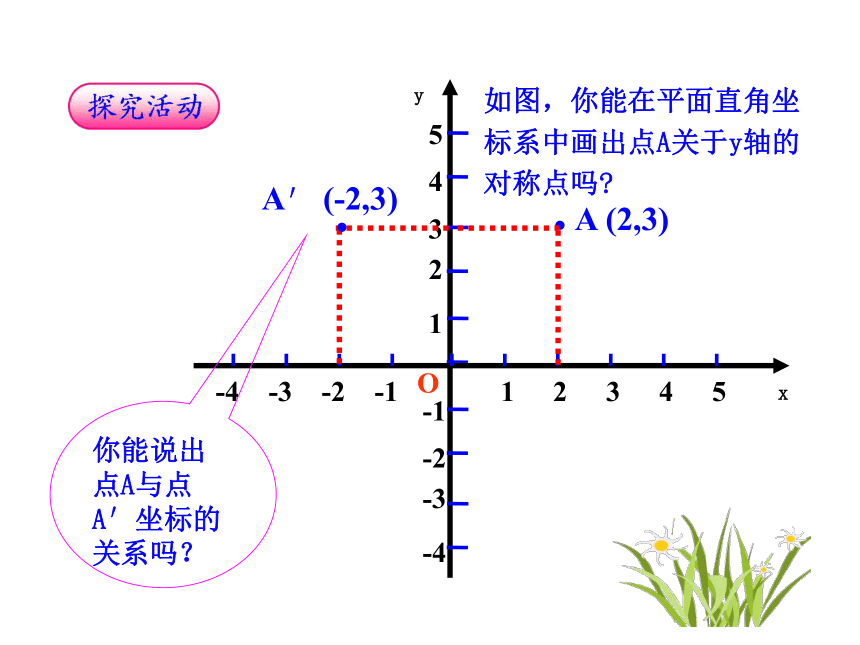
相同，纵坐标互为相反数.yxO·A (2,3)·A′ (-2,3)你能说出点A与点A′坐标的关系吗？如图，你能在平面直角坐
标系中画出点A关于y轴的
对称点吗?yxOB (-4, 2)··C(3, -4)·B′ (4, 2)·C′(-3, -4)关于y轴对
称的点的
坐标具有
怎样的关
系？在平面直角坐标系中画出下列各点关于y轴的对称点.yxO 关于y轴对称的点的横坐标互为相反数, 纵坐标
相等.点（x, y）关于x轴对称的点的坐标为________.
点（x, y）关于y轴对称的点的坐标为________.(x,－y)(－x,y)【解析】点A(-3,5),
B(-4,1),C(-1,3)，关于
y轴对称的点的坐标分别为
A′(3,5),B′(4,1),
C′(1,3).依次连接A′B′,B′C′,
C′A′,就得到△ABC关于y
轴对称的△A′B′C′.····A·C BB′A′C′已知△ABC的三个顶点的坐标分别为A(-3，5),B(-4，1),
C(-1，3)，作出△ABC关于y轴对称的图形.yx·【例 题】技巧:对于这类问题,只要先求出已知图形中的一些特殊
点(如多边形的顶点)的对应点的坐标,描出并连接这些点,
就可以得到这个图形的轴对称图形.1.点P(-5, 6)与点Q关于x轴对称，则点Q的坐标为__________.
2.点M(a, -5)与点N(-2, b)关于x轴对称，则a=_____,b =_____.(- 5 ,-6 )-25【跟踪训练】3.点P(-3, 2)与点Q关于y轴对称，则点Q的坐标为__________.
4.点M(a, -6)与点N(-2, b)关于y轴对称，则a=_____,
b =_____.( 3 , 2 )2-6运用变化规律作图　　例 如图，四边形ABCD 的四个顶点的坐标分别为
A（-5，1），B（-2，1），
C（-2，5），D（-5，4），
画出与四边形ABCD 关
于y 轴对称的图形．解：依次连接 , , , ,
就可得到与四边形ABCD
关于y轴对称的四边形
．A′B′C′D′ A′B′ B′C′ C′D′ D′A′ 1.关于x轴对称的点横坐标相等，纵坐标互为相反数.
关于y轴对称的点横坐标互为相反数，纵坐标相等. 2.在平面直角坐标系中画一个图形关于x轴或y轴的对
称图形：先求出已知图形中的一些特殊点(如多边形的顶
点)的对应点的坐标,描出并连接这些点,就可以得到这个
图形的轴对称图形. 通过本课时的学习，需要我们掌握：1.完成下表:(-3,-3)(3, 3)(-1,-2)(1, 2)(8,-5)(-8,5)(0, -1)(0,1)(-4,0)（4，0）2.已知点P(2a+b,-3a)与点P′(8,b+2).
若点P与点P′关于x轴对称，则a=_____,b=_______.
若点P与点P′关于y轴对称，则a=_____,b=_______.246-20x=1·····P(-2,3)M(-1,1)N′ (5,-2)N(-3,-2)M′ (3,1)P′(4,3)3.如图,分别
作出点P,M,N
关于直线x=1
的对称点,
你能发现它
们坐标之间
分别有什么
关系吗?·yx(-x+2,y)(-x-2,y)(x,-y+2)(x,-y-2)（1）在平面直角坐标系中,点(x,y)关于直线x=1对称的点的坐标是多少?（2）在平面直角坐标系中,点(x,y)关于直线x=-1对称的点的坐标是多少? （3）在平面直角坐标系中,点(x,y)关于直线y=1对称的点的坐标是多少?（4）在平面直角坐标系中,点(x,y)关于直线y=-1对称的点的坐标是多少? 成功：A=x+y+z.A代表成功，x代表艰苦的劳动，y代表正确的方法，Z代表少说空话.
——爱因斯坦