2.6等腰三角形(第1课时)(25张ppt)课件
文档属性
| 名称 | 2.6等腰三角形(第1课时)(25张ppt)课件 |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-01-23 09:48:06 | ||
图片预览







文档简介
课件25张PPT。第1课时2.6 等腰三角形下列图形不一定是轴对称图形的是( )
A.圆 B.长方形 C.线段 D.三角形D1.了解等腰三角形的概念,掌握等腰三角形的性质;
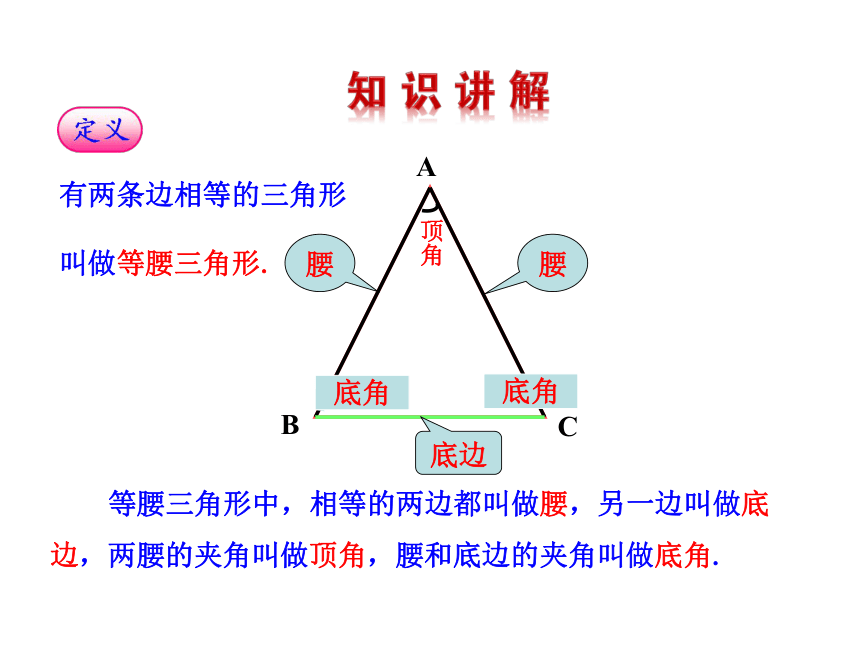
2.运用等腰三角形的概念及性质解决相关问题.有两条边相等的三角形
叫做等腰三角形. 等腰三角形中,相等的两边都叫做腰,另一边叫做底
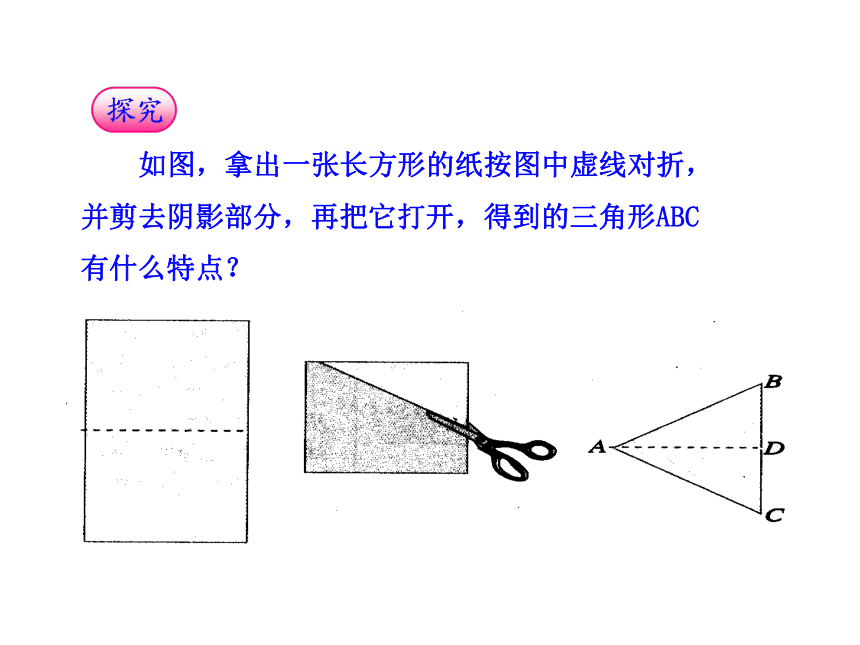
边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角.ACB底边 如图,拿出一张长方形的纸按图中虚线对折,
并剪去阴影部分,再把它打开,得到的三角形ABC
有什么特点?把剪出的等腰三角形ABC沿折痕
对折,找出其中重合的线段和角. AC B D AB=AC BD=CD AD=AD ∠B =∠C∠BAD=∠CAD∠ADB=∠ADC 等腰三角形除了两腰相等以外,你还能发现它的其他
性质吗?等腰三角形的两个底角相等.已知:△ABC中,AB=AC试说明:∠B=?C分析:1.如何说明两个角相等? 2.如何构造两个全等的三角形?D【解析】作△ABC的高线AD, (HL) 则有∠ADB=∠ADC=90°,在Rt△ABD和Rt△ACD中AB=AC, AD=AD, 所以 Rt△ABD≌Rt△ACD 所以 ∠B=∠C (全等三角形的对应角相等) 还有其他的方法吗?还可以作BC边上的中线或∠BAC的角平分线来解决 等腰三角形顶角的平分线,底边上的高、底边上的
中线有什么关系?
刚才的推理除了能得到∠B=∠C,你还能发现什么?(等腰三角形“三线合一”) 等腰三角形的顶角平分线、底边上的中线、底边上
的高互相重合.等腰三角形的性质 :性质1:等腰三角形是轴对称图形,等腰三角形的对称轴
是底边的垂直平分线.
性质2:等腰三角形的两个底角相等(简写成“等边对等
角”)
性质3:等腰三角形的顶角平分线、底边上的中线、底边
上的高相互重合.(简写成“三线合一”)例题讲解例题1:如图2-39,屋椽AB和AC的长相等,∠A=120o,求∠B的度数。巩固练习(1)⒈等腰三角形一个底角为75°,它的另外两个
角为_____ __;
⒉等腰三角形一个角为70°,它的另外两个角
为___________________;
⒊等腰三角形一个角为110°,它的另外两个角
为______ __。
75°, 30°70°,40°或 55°,55°35°,35°例2 如图,在△ABC中 ,AB=AC,点D在AC上,且BD=BC=AD,
求△ABC各角的度数.【练习】【解析】因为AB=AC,BD=BC=AD,
所以∠ABC=∠C=∠BDC,∠A=∠ABD (等边对等角)
设∠A=x,则∠BDC=∠A+∠ABD=2x,
从而∠ABC=∠C=∠BDC=2x,
于是在△ABC中,有∠A+∠ABC+∠C=x+2x+2x=180°,
解得x=36°,
所以,在△ABC中,∠A=36°,∠ABC=∠C=72°.⒈等腰三角形一个底角为50°,它的另外两个角为_____________;
⒉等腰三角形一个角为70°,它的另外两个角为___________________;
⒊等腰三角形一个角为120°,它的另外两个角为
________.50°, 80°70°,40°或55°,55°30°,30°【跟踪训练】两个底角相等,简称“等边对等角”顶角平分线、底边上的中线和底边上的高互相
重合,简称“三线合 一” 轴对称图形等腰三角形的性质1.(烟台·中考)如图,等腰△ABC中,AB=AC,∠A=20°.
线段AB的垂直平分线交AB于D,交AC于E,连接BE,则∠CBE
等于( )
A.80° B. 70° C.60° D.50°
【解析】选C. 因为AB=AC,∠A=20°,所以∠ABC=
(180°-∠A)=80°,因为DE垂直平分AB,所以∠ABE=∠A=20°,所以∠CBE=∠ABC-∠ABE=80°-20°=60°.达标检测2.(日照·中考)已知等腰梯形的底角为45°,
高为2,上底为2,则其面积为( )
A.2 B.6 C.8 D.12【解析】选C.过上底的两个顶点分别作下底的垂线,又因
为底角为45°,高为2,则下底的长等于2+2+2=6,
S=(2+6)×2=8. 3.(泰州·中考)等腰△ABC的两边长为2和5,则第三边
长为 .
【解析】因为2,5,5能构成三角形,2,2,5不能构成三角
形,所以第三边长为5.
答案:5 因为宇宙的结构是最完善的而且是最明智的上帝的创造,因此,如果在宇宙里没有某种极大的或极小的法则,那就根本不会发生任何事情.
——欧拉
A.圆 B.长方形 C.线段 D.三角形D1.了解等腰三角形的概念,掌握等腰三角形的性质;
2.运用等腰三角形的概念及性质解决相关问题.有两条边相等的三角形
叫做等腰三角形. 等腰三角形中,相等的两边都叫做腰,另一边叫做底
边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角.ACB底边 如图,拿出一张长方形的纸按图中虚线对折,
并剪去阴影部分,再把它打开,得到的三角形ABC
有什么特点?把剪出的等腰三角形ABC沿折痕
对折,找出其中重合的线段和角. AC B D AB=AC BD=CD AD=AD ∠B =∠C∠BAD=∠CAD∠ADB=∠ADC 等腰三角形除了两腰相等以外,你还能发现它的其他
性质吗?等腰三角形的两个底角相等.已知:△ABC中,AB=AC试说明:∠B=?C分析:1.如何说明两个角相等? 2.如何构造两个全等的三角形?D【解析】作△ABC的高线AD, (HL) 则有∠ADB=∠ADC=90°,在Rt△ABD和Rt△ACD中AB=AC, AD=AD, 所以 Rt△ABD≌Rt△ACD 所以 ∠B=∠C (全等三角形的对应角相等) 还有其他的方法吗?还可以作BC边上的中线或∠BAC的角平分线来解决 等腰三角形顶角的平分线,底边上的高、底边上的
中线有什么关系?
刚才的推理除了能得到∠B=∠C,你还能发现什么?(等腰三角形“三线合一”) 等腰三角形的顶角平分线、底边上的中线、底边上
的高互相重合.等腰三角形的性质 :性质1:等腰三角形是轴对称图形,等腰三角形的对称轴
是底边的垂直平分线.
性质2:等腰三角形的两个底角相等(简写成“等边对等
角”)
性质3:等腰三角形的顶角平分线、底边上的中线、底边
上的高相互重合.(简写成“三线合一”)例题讲解例题1:如图2-39,屋椽AB和AC的长相等,∠A=120o,求∠B的度数。巩固练习(1)⒈等腰三角形一个底角为75°,它的另外两个
角为_____ __;
⒉等腰三角形一个角为70°,它的另外两个角
为___________________;
⒊等腰三角形一个角为110°,它的另外两个角
为______ __。
75°, 30°70°,40°或 55°,55°35°,35°例2 如图,在△ABC中 ,AB=AC,点D在AC上,且BD=BC=AD,
求△ABC各角的度数.【练习】【解析】因为AB=AC,BD=BC=AD,
所以∠ABC=∠C=∠BDC,∠A=∠ABD (等边对等角)
设∠A=x,则∠BDC=∠A+∠ABD=2x,
从而∠ABC=∠C=∠BDC=2x,
于是在△ABC中,有∠A+∠ABC+∠C=x+2x+2x=180°,
解得x=36°,
所以,在△ABC中,∠A=36°,∠ABC=∠C=72°.⒈等腰三角形一个底角为50°,它的另外两个角为_____________;
⒉等腰三角形一个角为70°,它的另外两个角为___________________;
⒊等腰三角形一个角为120°,它的另外两个角为
________.50°, 80°70°,40°或55°,55°30°,30°【跟踪训练】两个底角相等,简称“等边对等角”顶角平分线、底边上的中线和底边上的高互相
重合,简称“三线合 一” 轴对称图形等腰三角形的性质1.(烟台·中考)如图,等腰△ABC中,AB=AC,∠A=20°.
线段AB的垂直平分线交AB于D,交AC于E,连接BE,则∠CBE
等于( )
A.80° B. 70° C.60° D.50°
【解析】选C. 因为AB=AC,∠A=20°,所以∠ABC=
(180°-∠A)=80°,因为DE垂直平分AB,所以∠ABE=∠A=20°,所以∠CBE=∠ABC-∠ABE=80°-20°=60°.达标检测2.(日照·中考)已知等腰梯形的底角为45°,
高为2,上底为2,则其面积为( )
A.2 B.6 C.8 D.12【解析】选C.过上底的两个顶点分别作下底的垂线,又因
为底角为45°,高为2,则下底的长等于2+2+2=6,
S=(2+6)×2=8. 3.(泰州·中考)等腰△ABC的两边长为2和5,则第三边
长为 .
【解析】因为2,5,5能构成三角形,2,2,5不能构成三角
形,所以第三边长为5.
答案:5 因为宇宙的结构是最完善的而且是最明智的上帝的创造,因此,如果在宇宙里没有某种极大的或极小的法则,那就根本不会发生任何事情.
——欧拉
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
