一次函数的应用分层练习

《一次函数的应用》分层练习
根据本校学生及教学情况可在教学过程中，选择以下内容进行补充或拓展。
基础训练
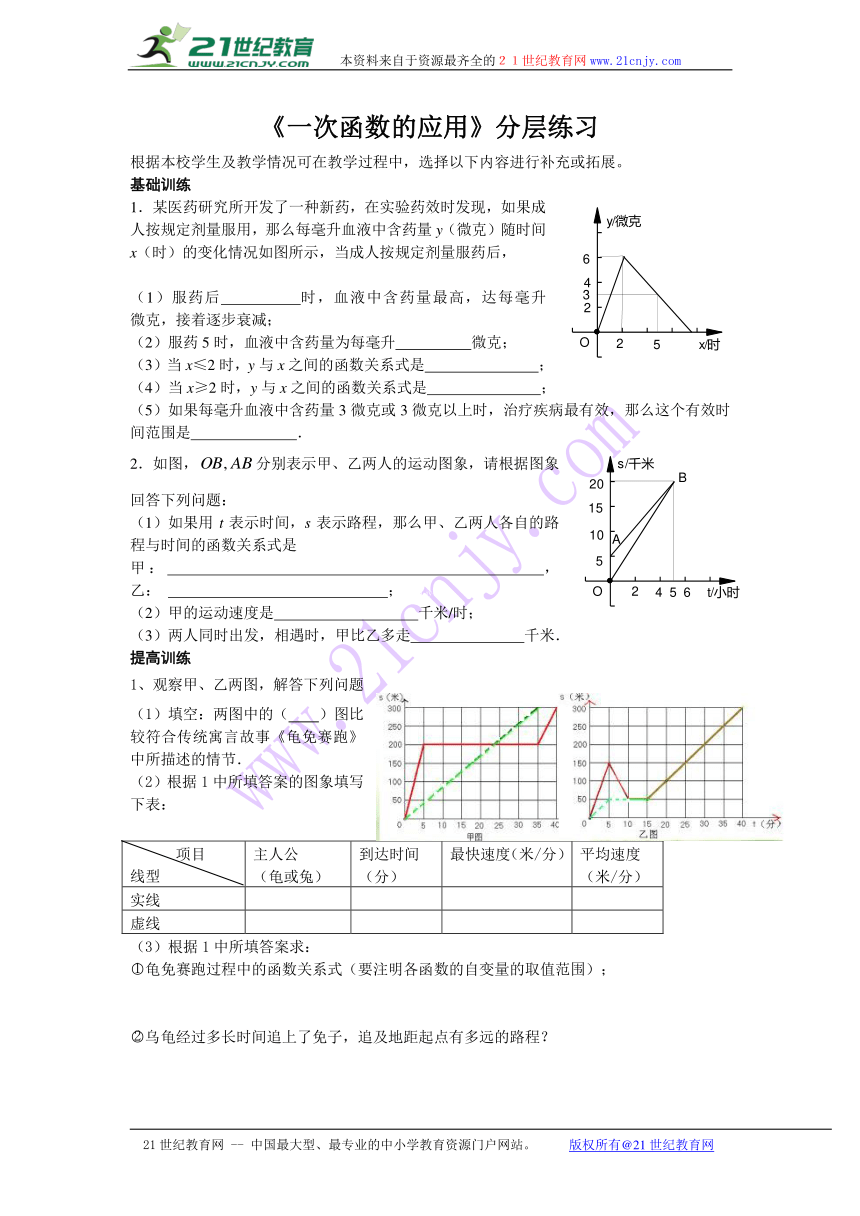
1．某医药研究所开发了一种新药，在实验药效时发现，如果成人按规定剂量服用，那么每毫升血液中含药量y（微克）随时间x（时）的变化情况如图所示，当成人按规定剂量服药后，21教育网
（1）服药后 时，血液中含药量最高，达每毫升 微克，接着逐步衰减；
（2）服药5时，血液中含药量为每毫升 微克；
（3）当x≤2时，y与x之间的函数关系式是 ；
（4）当x≥2时，y与x之间的函数关系式是 ；
（5）如果每毫升血液中含药量3微克或3微克以上时，治疗疾病最有效，那么这个有效时间范围是 ．21cnjy.com
2．如图，分别表示甲、乙两人的运动图象，请根据图象回答下列问题：
（1）如果用t表示时间，s表示路程，那么甲、乙两人各自的路程与时间的函数关系式是
甲： ，乙： ；21·cn·jy·com
（2）甲的运动速度是 千米/时；
（3）两人同时出发，相遇时，甲比乙多走 千米．
提高训练
1、观察甲、乙两图，解答下列问题
（1）填空：两图中的（ ）图比较符合传统寓言故事《龟免赛跑》中所描述的情节．
（2）根据1中所填答案的图象填写下表：
项目
主人公
（龟或兔）
到达时间（分）
最快速度（米/分）
平均速度（米/分）
实线
虚线
（3）根据1中所填答案求：
龟免赛跑过程中的函数关系式（要注明各函数的自变量的取值范围）；
乌龟经过多长时间追上了免子，追及地距起点有多远的路程？
2、某电视机厂要印刷产品宣传材料，甲印刷厂提出：每份材料收1元印刷费，另收1500元制版费；乙印刷厂提出：每份材料收2.5元印刷费，不收制版费．
（1）分别写出两厂的收费（元）与印制数量（份）之间的关系式；
（2）在同一直角坐标系内作出它们的图象；
（3）根据图象回答下列问题：
① 印制800份宣传材料时，选择哪家印刷厂比较合算？
② 电视机厂拟拿出3000元用于印刷宣传材料，找哪家印刷厂印刷宣传材料能多些？
3、生态公园计划在园内的坡地上造一片有两种树的混合林，需要购买这两种树苗2000棵．种植两种树苗的相关信息如下表：设购买种树苗棵，造这片林的总费用为元．解答下列问题：（1）写出（元）与（棵）之间的函数关系式；
单价（元/棵）
成活率
劳务费（元/棵）
A
15
3
B
20
4
（2）假设这批树苗种植后成活1960棵，则造这片林的总费用需多少元？
4、如图，lA与 lB分别表示步行与骑车同一路上行驶的路程与时间的关系．
（1）出发时与相距多少千米？
（2）走了一段路后，自行车发生故障，进行修理，所用的时间是多少小时？
（3）出发后经过多少小时与相遇？
（4）若的自行车不发生故障，保持出发时的速度前进，那么经
过多少时间与相遇？相遇点离的出发点多远？你能用哪些方法
解决这个问题？在图中表示出这个相遇点．
视野拓展
抗震救灾中，某县粮食局为了保证库存粮食的安全，决定将甲、乙两个仓库的粮食，全部转移到具有较强抗震功能的,两仓库。已知甲库有粮食100吨，乙库有粮食80吨，而库的容量为70吨，库的容量为110吨。从甲、乙两库到，两库的路程和运费如下表（表中“元/吨·千米”表示每吨粮食运送1千米所需人民币）21世纪教育网版权所有

（1）若甲库运往库粮食吨，请写出将粮食运往A、两库的总运费（元）与（吨）的函数关系式
（2）当甲、乙两库各运往、两库多少吨粮食时，总运费最省，最省的总运费是多少？