山东省滨州市三校2016-2017学年八年级(上)第三次月考数学试卷(解析版)
文档属性
| 名称 | 山东省滨州市三校2016-2017学年八年级(上)第三次月考数学试卷(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 237.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-01-28 00:00:00 | ||
图片预览




文档简介
2016-2017学年山东省滨州市三校八年级(上)第三次月考数学试卷
一、选择题(本大题有12小题,每小题3分,共36分,请把正确的选项填在答题卡的相应位置上.)
1.以下五家银行行标中,是轴对称图形的有( )
A.1个
B.2个
C.3个
D.4个
2.下列计算中正确的是( )
A.a2+b3=2a5
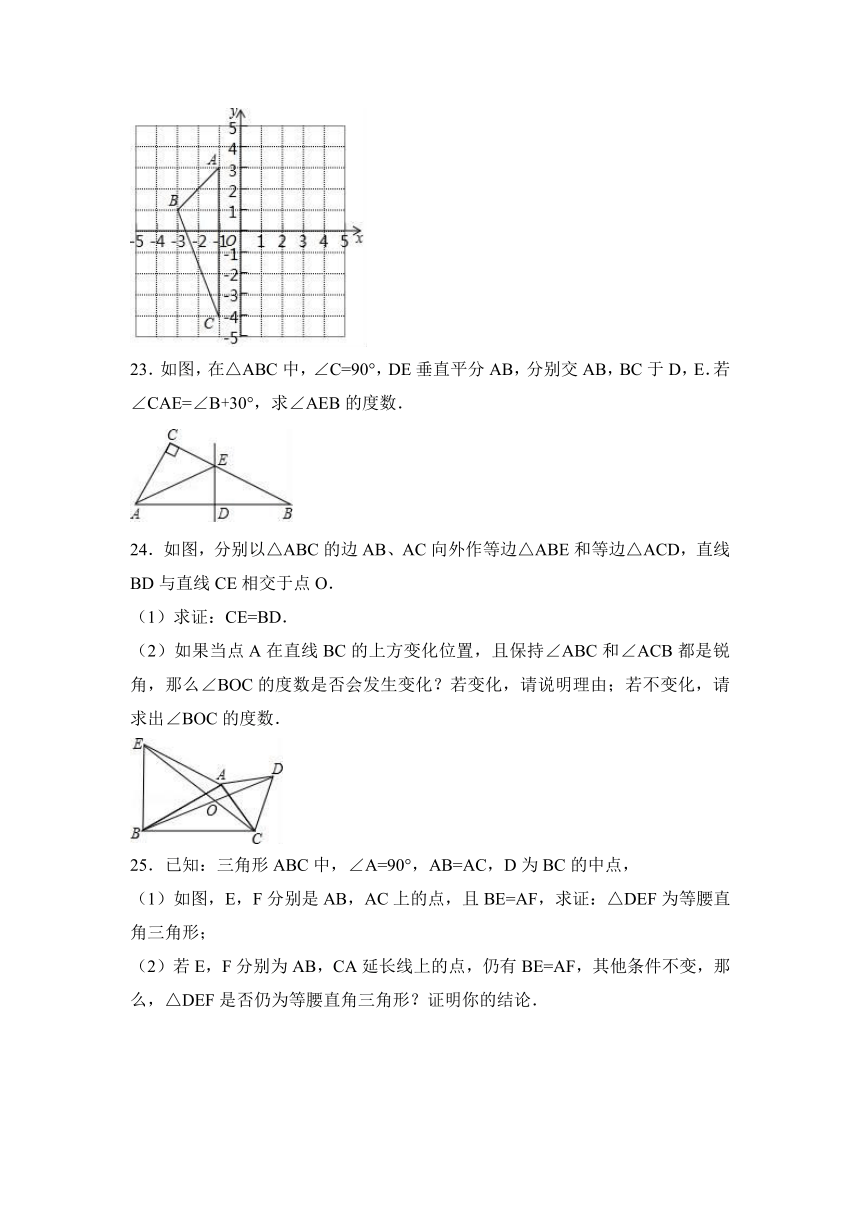
B.a4÷a=a4
C.a2 a4=a8
D.(﹣a2)3=﹣a6
3.已知三角形的两边长分别为3cm和8cm,则此三角形的第三边的长可能是( )
A.4cm
B.5cm
C.6cm
D.13cm
4.n边形的内角和与外角和相等,则n=( )
A.3
B.4
C.5
D.6
5.若等腰三角形的周长为26cm,一边为11cm,则腰长为( )
A.11cm
B.7.5cm
C.11cm或7.5cm
D.以上都不对
6.如图,已知点A、D、C、F在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加一个条件是( )
A.∠BCA=∠F
B.∠B=∠E
C.BC∥EF
D.∠A=∠EDF
7.把多项式x3﹣2x2+x分解因式结果正确的是( )
A.x(x2﹣2x)
B.x2(x﹣2)
C.x(x+1)(x﹣1)
D.x(x﹣1)2
8.如图,△ABC中边AB的垂直平分线分别交BC,AB于点D,E,AE=3cm,△ADC的周长为9cm,则△ABC的周长是( )
A.10cm
B.12cm
C.15cm
D.17cm
9.如果(x+1)(x2﹣5ax+a)的乘积中不含x2项,则a为( )
A.
B.﹣
C.﹣5
D.5
10.如图,C、E和B、D、F分别在∠GAH的两边上,且AB=BC=CD=DE=EF,若∠A=18°,则∠GEF的度数为( )
A.75°
B.80°
C.85°
D.90°
11.若x=1,,则x2+4xy+4y2的值是( )
A.2
B.4
C.
D.
12.若x2﹣3x=1,则代数式x4﹣6x3+9x2+2016的值是( )
A.2015
B.2016
C.2017
D.2018
二、填空题(本大题有6小题,每小题4分,共24分)
13.小明从镜子里看到镜子对面电子钟的像,如图所示,实际时间是
14.若点A(m+2,﹣3)与点B(4,n+5)关于x轴对称,则(mn)2= .
15.若4x2﹣2kx+1是完全平方式,则k= .
16.如图,在△ABC中,∠C是直角,AD平分∠BAC交BC于点D.如果AB=8,CD=2那么△ABD的面积等于 .
17.如图,△ABC中,∠A=65°,∠B=75°,将△ABC沿EF对折,使C点与C′点重合.当∠1=45°时,∠2= °.
18.观察下列各式:
1×3+1=4=22
2×4+1=9=32
3×5+1=16=42
4×6+1=25=52
…
请你把发现的规律用含正整数n的等式表示为 .
三、解答题(本大题共有7个小题,共60分)
19.分解因式:
(1)a3﹣ab2
(2)3ax2﹣6axy+3ay2.
20.计算:
(1)(3x﹣2)(2x+3)﹣(x﹣1)2;
(2)12ab2(abc)4÷(﹣3a2b3c)÷[2(abc)3].
21.先化简,再求值:[(x﹣2y)2﹣x(x﹣4y)﹣8xy]÷4y,其中x=﹣1,y=2.
22.在边长为1的小正方形组成的正方形网格中建立如图所示的平面直角坐标系,已知格点三角形ABC(三角形的三个顶点都在小正方形的顶点上).
(1)写出△ABC的面积: .
(2)画出△ABC关于y轴对称的△A1B1C1.
(3)写出点B及其对称点B1的坐标. ; .
23.如图,在△ABC中,∠C=90°,DE垂直平分AB,分别交AB,BC于D,E.若∠CAE=∠B+30°,求∠AEB的度数.
24.如图,分别以△ABC的边AB、AC向外作等边△ABE和等边△ACD,直线BD与直线CE相交于点O.
(1)求证:CE=BD.
(2)如果当点A在直线BC的上方变化位置,且保持∠ABC和∠ACB都是锐角,那么∠BOC的度数是否会发生变化?若变化,请说明理由;若不变化,请求出∠BOC的度数.
25.已知:三角形ABC中,∠A=90°,AB=AC,D为BC的中点,
(1)如图,E,F分别是AB,AC上的点,且BE=AF,求证:△DEF为等腰直角三角形;
(2)若E,F分别为AB,CA延长线上的点,仍有BE=AF,其他条件不变,那么,△DEF是否仍为等腰直角三角形?证明你的结论.
2016-2017学年山东省滨州市三校八年级(上)第三次月考数学试卷
参考答案与试题解析
一、选择题(本大题有12小题,每小题3分,共36分,请把正确的选项填在答题卡的相应位置上.)
1.以下五家银行行标中,是轴对称图形的有( )
A.1个
B.2个
C.3个
D.4个
【考点】轴对称图形.
【分析】轴对称图形的概念:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴,这时,我们也可以说这个图形关于这条直线(成轴)对称可得答案.
【解答】解:第一、二、三个图形是轴对称图形,第四、五个图形不是轴对称图形,
故选:C.
2.下列计算中正确的是( )
A.a2+b3=2a5
B.a4÷a=a4
C.a2 a4=a8
D.(﹣a2)3=﹣a6
【考点】同底数幂的除法;合并同类项;同底数幂的乘法;幂的乘方与积的乘方.
【分析】根据合并同类项,可判断A;根据同底数幂的除法,可判断B;根据同底数幂的乘法,可判断C;根据积的乘方,可判断D.
【解答】解:A、不是同类项不能合并,故A错误;
B、同底数幂的除法底数不变指数相减,故B错误;
C、同底数幂的乘法底数不变指数相加,故C错误;
D、积的乘方等于乘方的积,故D正确;
故选:D.
3.已知三角形的两边长分别为3cm和8cm,则此三角形的第三边的长可能是( )
A.4cm
B.5cm
C.6cm
D.13cm
【考点】三角形三边关系.
【分析】已知三角形的两边长分别为3cm和8cm,根据在三角形中任意两边之和>第三边,任意两边之差<第三边;即可求第三边长的范围.
【解答】解:设第三边长为x,则由三角形三边关系定理得8﹣3<x<8+3,即5<x<11.
因此,本题的第三边应满足5<x<11,把各项代入不等式符合的即为答案.
4,5,13都不符合不等式5<x<11,只有6符合不等式,故答案为6cm.故选C.
4.n边形的内角和与外角和相等,则n=( )
A.3
B.4
C.5
D.6
【考点】多边形内角与外角.
【分析】n边形的内角和为:(n﹣2)×180°,外角和为360°,列式计算.
【解答】解:由题意得:(n﹣2)×180=360,
n=4,
故选B.
5.若等腰三角形的周长为26cm,一边为11cm,则腰长为( )
A.11cm
B.7.5cm
C.11cm或7.5cm
D.以上都不对
【考点】等腰三角形的性质.
【分析】分边11cm是腰长与底边两种情况讨论求解.
【解答】解:①11cm是腰长时,腰长为11cm,
②11cm是底边时,腰长=(26﹣11)=7.5cm,
所以,腰长是11cm或7.5cm.
故选C.
6.如图,已知点A、D、C、F在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加一个条件是( )
A.∠BCA=∠F
B.∠B=∠E
C.BC∥EF
D.∠A=∠EDF
【考点】全等三角形的判定.
【分析】全等三角形的判定方法SAS是指有两边对应相等,且这两边的夹角相等的两三角形全等,已知AB=DE,BC=EF,其两边的夹角是∠B和∠E,只要求出∠B=∠E即可.
【解答】解:A、根据AB=DE,BC=EF和∠BCA=∠F不能推出△ABC≌△DEF,故本选项错误;
B、∵在△ABC和△DEF中
,
∴△ABC≌△DEF(SAS),故本选项正确;
C、∵BC∥EF,
∴∠F=∠BCA,根据AB=DE,BC=EF和∠F=∠BCA不能推出△ABC≌△DEF,故本选项错误;
D、根据AB=DE,BC=EF和∠A=∠EDF不能推出△ABC≌△DEF,故本选项错误.
故选B.
7.把多项式x3﹣2x2+x分解因式结果正确的是( )
A.x(x2﹣2x)
B.x2(x﹣2)
C.x(x+1)(x﹣1)
D.x(x﹣1)2
【考点】提公因式法与公式法的综合运用.
【分析】这个多项式含有公因式x,应先提取公因式,然后再按完全平分公式进行二次分解.
【解答】解:原式=x(x2﹣2x+1)=x(x﹣1)2.
故选D.
8.如图,△ABC中边AB的垂直平分线分别交BC,AB于点D,E,AE=3cm,△ADC的周长为9cm,则△ABC的周长是( )
A.10cm
B.12cm
C.15cm
D.17cm
【考点】线段垂直平分线的性质.
【分析】求△ABC的周长,已经知道AE=3cm,则知道AB=6cm,只需求得BC+AC即可,根据线段垂直平分线的性质得AD=BD,于是BC+AC等于△ADC的周长,答案可得.
【解答】解:∵AB的垂直平分AB,
∴AE=BE,BD=AD,
∵AE=3cm,△ADC的周长为9cm,
∴△ABC的周长是9+2×3=15cm,
故选:C.
9.如果(x+1)(x2﹣5ax+a)的乘积中不含x2项,则a为( )
A.
B.﹣
C.﹣5
D.5
【考点】多项式乘多项式.
【分析】先根据多项式乘以多项式的法则展开,再合并同类项,根据已知得出方程﹣5a+1=0,求出即可.
【解答】解:(x+1)(x2﹣5ax+a)
=x3﹣5ax2+ax+x2﹣5ax+a
=x3+(﹣5a+1)x2+ax+a,
∵(x+1)(x2﹣5ax+a)的乘积中不含x2项,
∴﹣5a+1=0,
a=,
故选A.
10.如图,C、E和B、D、F分别在∠GAH的两边上,且AB=BC=CD=DE=EF,若∠A=18°,则∠GEF的度数为( )
A.75°
B.80°
C.85°
D.90°
【考点】等腰三角形的性质;三角形的外角性质.
【分析】由AB=BC=CD=DE=EF,根据等腰三角形的性质:等边对等角,可得∠ACB=∠A,∠CDB=∠CBD,∠CED=∠DCE,∠EFD=∠EDF,又由三角形外角的性质与∠A=18°,即可求得∠GEF的度数.
【解答】解:∵AB=BC,
∴∠ACB=∠A=18°,
∴∠CBD=∠A+∠ACB=36°,
∵BC=CD,
∴∠CDB=∠CBD=36°,
∴∠DCE=∠A+∠CDA=18°+36°=54°,
∵CD=DE,
∴∠CED=∠DCE=54°,
∴∠EDF=∠A+∠AED=18°+54°=72°,
∵DE=EF,
∴∠EFD=∠EDF=72°,
∴∠GEF=∠A+∠AFE=18°+72°=90°.
故选D.
11.若x=1,,则x2+4xy+4y2的值是( )
A.2
B.4
C.
D.
【考点】完全平方公式.
【分析】首先用完全平方公式将原式化简,然后再代值计算.
【解答】解:原式=(x+2y)2=(1+2×)2=4.
故选B.
12.若x2﹣3x=1,则代数式x4﹣6x3+9x2+2016的值是( )
A.2015
B.2016
C.2017
D.2018
【考点】因式分解的应用.
【分析】先将代数式进行适当的变形,然后将x2﹣3x=1代入即可求出答案.
【解答】解:∵x2﹣3x=1,
∴原式=x2(x2﹣6x+9)+2016
=x2(x﹣3)2+2016
=[x(x﹣3)]2+2016
=(x2﹣3x)2+2016
=2017
故选(C)
二、填空题(本大题有6小题,每小题4分,共24分)
13.小明从镜子里看到镜子对面电子钟的像,如图所示,实际时间是 10:51
【考点】镜面对称.
【分析】根据镜面对称的性质求解,在平面镜中的像与现实中的事物恰好左右或上下顺序颠倒,且关于镜面对称.
【解答】解:根据镜面对称的性质,分析可得题中所显示的图片与10:51成轴对称,所以此时实际时刻为10:51.故答案为10:51.
14.若点A(m+2,﹣3)与点B(4,n+5)关于x轴对称,则(mn)2= 16 .
【考点】关于x轴、y轴对称的点的坐标.
【分析】关于x轴对称的点,横坐标相同,纵坐标互为相反数
【解答】解:由题意,得
m+2=4,n+5=3,
解得m=﹣2,n=﹣2.
(mn)2=[﹣2×(﹣2)]2=16,
故答案为:16.
15.若4x2﹣2kx+1是完全平方式,则k= ±2 .
【考点】完全平方式.
【分析】这里首末两项是2x和1这两个数的平方,那么中间一项为加上或减去2x和1积的2倍.
【解答】解:∵4x2﹣2kx+1是完全平方式,
∵4x2±4x+1=(2x±1)2是完全平方式,
∴﹣2k=±4,
解得k=±2.
16.如图,在△ABC中,∠C是直角,AD平分∠BAC交BC于点D.如果AB=8,CD=2那么△ABD的面积等于 8 .
【考点】角平分线的性质;三角形的面积.
【分析】过点D作DE⊥AB,由角平分线的性质可知DE=CD=2,再根据S△ABD=AB DE即可得出结论.
【解答】解:过点D作DE⊥AB,
∵AD平分∠BAC,
∴DE=CD=2,
∴S△ABD=AB DE=×8×2=8.
故答案为:8.
17.如图,△ABC中,∠A=65°,∠B=75°,将△ABC沿EF对折,使C点与C′点重合.当∠1=45°时,∠2= 35 °.
【考点】三角形内角和定理;翻折变换(折叠问题).
【分析】由△ABC中,∠A=65°,∠B=75°,可求得∠C的度数,又由三角形内角和定理,求得∠CEF+∠CFE,继而求得∠C′EF+∠C′FE,则可求得∠1+∠2,继而求得答案.
【解答】解:∵△ABC中,∠A=65°,∠B=75°,
∴∠C=180°﹣(∠A+∠B)=40°,
∴∠CEF+∠CFE=180°﹣∠C=140°,
∵将△ABC沿EF对折,使C点与C′点重合,
∴∠C′EF+∠C′FE=∠CEF+∠CFE=140°,
∴∠1+∠2=360°﹣(∠C′EF+∠C′FE+∠CEF+∠CFE)=80°,
∵∠1=45°,
∴∠2=35°.
故答案为:35.
18.观察下列各式:
1×3+1=4=22
2×4+1=9=32
3×5+1=16=42
4×6+1=25=52
…
请你把发现的规律用含正整数n的等式表示为 n(n+2)+1=(n+1)2 .
【考点】规律型:数字的变化类.
【分析】观察不难发现,一个数前后两个数的积加上1等于这个数的平方,根据此规律写出即可.
【解答】解:∵1×3+1=4=22,
2×4+1=9=32,
3×5+1=16=42,
4×6+1=25=52,
…
∴用含正整数n的等式表示为n(n+2)+1=(n+1)2.
故答案为:n(n+2)+1=(n+1)2.
三、解答题(本大题共有7个小题,共60分)
19.分解因式:
(1)a3﹣ab2
(2)3ax2﹣6axy+3ay2.
【考点】提公因式法与公式法的综合运用.
【分析】(1)先提取公因式a,再对余下的多项式利用平方差公式继续分解;
(2)先提取公因式3a,再对余下的多项式利用完全平方公式继续分解.
【解答】解:(1)a3﹣ab2
=a(a2﹣b2)
=a(a+b)(a﹣b);
(2)3ax2﹣6axy+3ay2
=3a(x2﹣2xy+y2)
=3a(x﹣y)2.
20.计算:
(1)(3x﹣2)(2x+3)﹣(x﹣1)2;
(2)12ab2(abc)4÷(﹣3a2b3c)÷[2(abc)3].
【考点】整式的混合运算.
【分析】(1)原式第一项利用多项式乘多项式法则计算,第二项利用完全平方公式展开,去括号合并即可得到结果;
(2)原式利用幂的乘方及积的乘方运算法则计算,再利用单项式除以单项式法则计算即可得到结果.
【解答】解:(1)原式=6x2+9x﹣4x﹣6﹣x2+2x﹣1=5x2+7x﹣7;
(2)原式=12a5b6c4÷(﹣3a2b3c)÷(2a3b3c3)=﹣2c2.
21.先化简,再求值:[(x﹣2y)2﹣x(x﹣4y)﹣8xy]÷4y,其中x=﹣1,y=2.
【考点】整式的混合运算—化简求值.
【分析】原式中括号中第一项利用完全平方公式展开,第二项利用单项式乘以多项式法则计算,合并后利用多项式除以单项式法则计算得到最简结果,将x与y的值代入计算即可求出值.
【解答】解:原式=(x2﹣4xy+4y2﹣x2+4xy﹣8xy)÷4y=(4y2﹣12xy)÷4y=y﹣3x,
当x=﹣1,y=2时,原式=2+3=5.
22.在边长为1的小正方形组成的正方形网格中建立如图所示的平面直角坐标系,已知格点三角形ABC(三角形的三个顶点都在小正方形的顶点上).
(1)写出△ABC的面积: 7 .
(2)画出△ABC关于y轴对称的△A1B1C1.
(3)写出点B及其对称点B1的坐标. (﹣3,1) ; (3,1) .
【考点】作图-轴对称变换.
【分析】(1)根据图形结合坐标系可得△ABC的底AC为7,高为2,进而可得面积;
(2)首先确定A、B、C三点关于y轴的对称点位置,然后再连接即可;
(3)根据坐标系可得答案.
【解答】解:(1)2×7=7,
故答案为:7;
(2)如图所示:
(3)B(﹣3,1),B1(3,1),
故答案为:(﹣3,1);(3,1)
23.如图,在△ABC中,∠C=90°,DE垂直平分AB,分别交AB,BC于D,E.若∠CAE=∠B+30°,求∠AEB的度数.
【考点】线段垂直平分线的性质.
【分析】根据线段垂直平分线求出AE=BE,推出∠B=∠EAB,根据已知和三角形内角和定理得出∠B+30°+∠B+∠B=90°,求出∠B,即可得出答案.
【解答】解:∵DE垂直平分AB,
∴AE=BE,
∴∠B=∠EAB,
∵∠C=90°,∠CAE=∠B+30°,
∴∠B+30°+∠B+∠B=90°,
∴∠B=20°,
∴∠AEB=180°﹣20°﹣20°=140°.
24.如图,分别以△ABC的边AB、AC向外作等边△ABE和等边△ACD,直线BD与直线CE相交于点O.
(1)求证:CE=BD.
(2)如果当点A在直线BC的上方变化位置,且保持∠ABC和∠ACB都是锐角,那么∠BOC的度数是否会发生变化?若变化,请说明理由;若不变化,请求出∠BOC的度数.
【考点】全等三角形的判定与性质;等边三角形的性质.
【分析】(1)根据等边三角形的性质可得AB=AE,AC=AD,∠CAD=∠BAE=60°,再求出∠BAD=∠EAC,然后利用“边角边”证明△ABD和△AEC全等,根据全等三角形对应边相等证明即可;
(2)根据全等三角形对应角相等可得∠AEC=∠ABD,然后求出∠OEB+∠OBE=∠AEB+∠ABE,再根据三角形的一个外角等于与它不相邻的两个内角的和解答.
【解答】(1)证明:∵△ABE和△ACD都是等边三角形,
∴AB=AE,AC=AD,∠CAD=∠BAE=60°,
∵∠BAD=∠CAD+∠BAC,∠EAC=∠BAE+∠BAC,
∴∠BAD=∠EAC,
在△ABD和△AEC中,,
∴△ABD≌△AEC(SAS),
∴CE=BD;
(2)解:由(1)知,△ABD≌△AEC,
∴∠AEC=∠ABD,
又∵△ABE是等边三角形,
∴∠AEB=∠ABE=60°,
∴∠OEB+∠OBE=∠AEB+∠ABE=60°+60°=120°,
在△BOE中,∠BOC=∠OEB+∠OBE=120°,
故∠BOC的度数不会发生变化;
25.已知:三角形ABC中,∠A=90°,AB=AC,D为BC的中点,
(1)如图,E,F分别是AB,AC上的点,且BE=AF,求证:△DEF为等腰直角三角形;
(2)若E,F分别为AB,CA延长线上的点,仍有BE=AF,其他条件不变,那么,△DEF是否仍为等腰直角三角形?证明你的结论.
【考点】等腰直角三角形;全等三角形的判定与性质.
【分析】(1)先连接AD,构造全等三角形:△BED和△AFD.AD是等腰直角三角形ABC底边上的中线,所以有∠CAD=∠BAD=45°,AD=BD=CD,而∠B=∠C=45°,所以∠B=∠DAF,再加上BE=AF,AD=BD,可证出:△BED≌△AFD,从而得出DE=DF,∠BDE=∠ADF,从而得出∠EDF=90°,即△DEF是等腰直角三角形;
(2)还是证明:△BED≌△AFD,主要证∠DAF=∠DBE(∠DBE=180°﹣45°=135°,∠DAF=90°+45°=135°),再结合两组对边对应相等,所以两个三角形全等.
【解答】(1)证明:连接AD,
∵AB=AC,∠BAC=90°,D为BC的中点,
∴AD⊥BC,BD=AD.
∴∠B=∠DAC=45°
又BE=AF,
∴△BDE≌△ADF(SAS).
∴ED=FD,∠BDE=∠ADF.
∴∠EDF=∠EDA+∠ADF=∠EDA+∠BDE=∠BDA=90°.
∴△DEF为等腰直角三角形.
(2)解:△DEF为等腰直角三角形.
证明:若E,F分别是AB,CA延长线上的点,如图所示:
连接AD,
∵AB=AC,
∴△ABC为等腰三角形,
∵∠BAC=90°,D为BC的中点,
∴AD=BD,AD⊥BC(三线合一),
∴∠DAC=∠ABD=45°.
∴∠DAF=∠DBE=135°.
又AF=BE,
∴△DAF≌△DBE(SAS).
∴FD=ED,∠FDA=∠EDB.
∴∠EDF=∠EDB+∠FDB=∠FDA+∠FDB=∠ADB=90°.
∴△DEF仍为等腰直角三角形.
2017年1月27日
一、选择题(本大题有12小题,每小题3分,共36分,请把正确的选项填在答题卡的相应位置上.)
1.以下五家银行行标中,是轴对称图形的有( )
A.1个
B.2个
C.3个
D.4个
2.下列计算中正确的是( )
A.a2+b3=2a5
B.a4÷a=a4
C.a2 a4=a8
D.(﹣a2)3=﹣a6
3.已知三角形的两边长分别为3cm和8cm,则此三角形的第三边的长可能是( )
A.4cm
B.5cm
C.6cm
D.13cm
4.n边形的内角和与外角和相等,则n=( )
A.3
B.4
C.5
D.6
5.若等腰三角形的周长为26cm,一边为11cm,则腰长为( )
A.11cm
B.7.5cm
C.11cm或7.5cm
D.以上都不对
6.如图,已知点A、D、C、F在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加一个条件是( )
A.∠BCA=∠F
B.∠B=∠E
C.BC∥EF
D.∠A=∠EDF
7.把多项式x3﹣2x2+x分解因式结果正确的是( )
A.x(x2﹣2x)
B.x2(x﹣2)
C.x(x+1)(x﹣1)
D.x(x﹣1)2
8.如图,△ABC中边AB的垂直平分线分别交BC,AB于点D,E,AE=3cm,△ADC的周长为9cm,则△ABC的周长是( )
A.10cm
B.12cm
C.15cm
D.17cm
9.如果(x+1)(x2﹣5ax+a)的乘积中不含x2项,则a为( )
A.
B.﹣
C.﹣5
D.5
10.如图,C、E和B、D、F分别在∠GAH的两边上,且AB=BC=CD=DE=EF,若∠A=18°,则∠GEF的度数为( )
A.75°
B.80°
C.85°
D.90°
11.若x=1,,则x2+4xy+4y2的值是( )
A.2
B.4
C.
D.
12.若x2﹣3x=1,则代数式x4﹣6x3+9x2+2016的值是( )
A.2015
B.2016
C.2017
D.2018
二、填空题(本大题有6小题,每小题4分,共24分)
13.小明从镜子里看到镜子对面电子钟的像,如图所示,实际时间是
14.若点A(m+2,﹣3)与点B(4,n+5)关于x轴对称,则(mn)2= .
15.若4x2﹣2kx+1是完全平方式,则k= .
16.如图,在△ABC中,∠C是直角,AD平分∠BAC交BC于点D.如果AB=8,CD=2那么△ABD的面积等于 .
17.如图,△ABC中,∠A=65°,∠B=75°,将△ABC沿EF对折,使C点与C′点重合.当∠1=45°时,∠2= °.
18.观察下列各式:
1×3+1=4=22
2×4+1=9=32
3×5+1=16=42
4×6+1=25=52
…
请你把发现的规律用含正整数n的等式表示为 .
三、解答题(本大题共有7个小题,共60分)
19.分解因式:
(1)a3﹣ab2
(2)3ax2﹣6axy+3ay2.
20.计算:
(1)(3x﹣2)(2x+3)﹣(x﹣1)2;
(2)12ab2(abc)4÷(﹣3a2b3c)÷[2(abc)3].
21.先化简,再求值:[(x﹣2y)2﹣x(x﹣4y)﹣8xy]÷4y,其中x=﹣1,y=2.
22.在边长为1的小正方形组成的正方形网格中建立如图所示的平面直角坐标系,已知格点三角形ABC(三角形的三个顶点都在小正方形的顶点上).
(1)写出△ABC的面积: .
(2)画出△ABC关于y轴对称的△A1B1C1.
(3)写出点B及其对称点B1的坐标. ; .
23.如图,在△ABC中,∠C=90°,DE垂直平分AB,分别交AB,BC于D,E.若∠CAE=∠B+30°,求∠AEB的度数.
24.如图,分别以△ABC的边AB、AC向外作等边△ABE和等边△ACD,直线BD与直线CE相交于点O.
(1)求证:CE=BD.
(2)如果当点A在直线BC的上方变化位置,且保持∠ABC和∠ACB都是锐角,那么∠BOC的度数是否会发生变化?若变化,请说明理由;若不变化,请求出∠BOC的度数.
25.已知:三角形ABC中,∠A=90°,AB=AC,D为BC的中点,
(1)如图,E,F分别是AB,AC上的点,且BE=AF,求证:△DEF为等腰直角三角形;
(2)若E,F分别为AB,CA延长线上的点,仍有BE=AF,其他条件不变,那么,△DEF是否仍为等腰直角三角形?证明你的结论.
2016-2017学年山东省滨州市三校八年级(上)第三次月考数学试卷
参考答案与试题解析
一、选择题(本大题有12小题,每小题3分,共36分,请把正确的选项填在答题卡的相应位置上.)
1.以下五家银行行标中,是轴对称图形的有( )
A.1个
B.2个
C.3个
D.4个
【考点】轴对称图形.
【分析】轴对称图形的概念:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴,这时,我们也可以说这个图形关于这条直线(成轴)对称可得答案.
【解答】解:第一、二、三个图形是轴对称图形,第四、五个图形不是轴对称图形,
故选:C.
2.下列计算中正确的是( )
A.a2+b3=2a5
B.a4÷a=a4
C.a2 a4=a8
D.(﹣a2)3=﹣a6
【考点】同底数幂的除法;合并同类项;同底数幂的乘法;幂的乘方与积的乘方.
【分析】根据合并同类项,可判断A;根据同底数幂的除法,可判断B;根据同底数幂的乘法,可判断C;根据积的乘方,可判断D.
【解答】解:A、不是同类项不能合并,故A错误;
B、同底数幂的除法底数不变指数相减,故B错误;
C、同底数幂的乘法底数不变指数相加,故C错误;
D、积的乘方等于乘方的积,故D正确;
故选:D.
3.已知三角形的两边长分别为3cm和8cm,则此三角形的第三边的长可能是( )
A.4cm
B.5cm
C.6cm
D.13cm
【考点】三角形三边关系.
【分析】已知三角形的两边长分别为3cm和8cm,根据在三角形中任意两边之和>第三边,任意两边之差<第三边;即可求第三边长的范围.
【解答】解:设第三边长为x,则由三角形三边关系定理得8﹣3<x<8+3,即5<x<11.
因此,本题的第三边应满足5<x<11,把各项代入不等式符合的即为答案.
4,5,13都不符合不等式5<x<11,只有6符合不等式,故答案为6cm.故选C.
4.n边形的内角和与外角和相等,则n=( )
A.3
B.4
C.5
D.6
【考点】多边形内角与外角.
【分析】n边形的内角和为:(n﹣2)×180°,外角和为360°,列式计算.
【解答】解:由题意得:(n﹣2)×180=360,
n=4,
故选B.
5.若等腰三角形的周长为26cm,一边为11cm,则腰长为( )
A.11cm
B.7.5cm
C.11cm或7.5cm
D.以上都不对
【考点】等腰三角形的性质.
【分析】分边11cm是腰长与底边两种情况讨论求解.
【解答】解:①11cm是腰长时,腰长为11cm,
②11cm是底边时,腰长=(26﹣11)=7.5cm,
所以,腰长是11cm或7.5cm.
故选C.
6.如图,已知点A、D、C、F在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加一个条件是( )
A.∠BCA=∠F
B.∠B=∠E
C.BC∥EF
D.∠A=∠EDF
【考点】全等三角形的判定.
【分析】全等三角形的判定方法SAS是指有两边对应相等,且这两边的夹角相等的两三角形全等,已知AB=DE,BC=EF,其两边的夹角是∠B和∠E,只要求出∠B=∠E即可.
【解答】解:A、根据AB=DE,BC=EF和∠BCA=∠F不能推出△ABC≌△DEF,故本选项错误;
B、∵在△ABC和△DEF中
,
∴△ABC≌△DEF(SAS),故本选项正确;
C、∵BC∥EF,
∴∠F=∠BCA,根据AB=DE,BC=EF和∠F=∠BCA不能推出△ABC≌△DEF,故本选项错误;
D、根据AB=DE,BC=EF和∠A=∠EDF不能推出△ABC≌△DEF,故本选项错误.
故选B.
7.把多项式x3﹣2x2+x分解因式结果正确的是( )
A.x(x2﹣2x)
B.x2(x﹣2)
C.x(x+1)(x﹣1)
D.x(x﹣1)2
【考点】提公因式法与公式法的综合运用.
【分析】这个多项式含有公因式x,应先提取公因式,然后再按完全平分公式进行二次分解.
【解答】解:原式=x(x2﹣2x+1)=x(x﹣1)2.
故选D.
8.如图,△ABC中边AB的垂直平分线分别交BC,AB于点D,E,AE=3cm,△ADC的周长为9cm,则△ABC的周长是( )
A.10cm
B.12cm
C.15cm
D.17cm
【考点】线段垂直平分线的性质.
【分析】求△ABC的周长,已经知道AE=3cm,则知道AB=6cm,只需求得BC+AC即可,根据线段垂直平分线的性质得AD=BD,于是BC+AC等于△ADC的周长,答案可得.
【解答】解:∵AB的垂直平分AB,
∴AE=BE,BD=AD,
∵AE=3cm,△ADC的周长为9cm,
∴△ABC的周长是9+2×3=15cm,
故选:C.
9.如果(x+1)(x2﹣5ax+a)的乘积中不含x2项,则a为( )
A.
B.﹣
C.﹣5
D.5
【考点】多项式乘多项式.
【分析】先根据多项式乘以多项式的法则展开,再合并同类项,根据已知得出方程﹣5a+1=0,求出即可.
【解答】解:(x+1)(x2﹣5ax+a)
=x3﹣5ax2+ax+x2﹣5ax+a
=x3+(﹣5a+1)x2+ax+a,
∵(x+1)(x2﹣5ax+a)的乘积中不含x2项,
∴﹣5a+1=0,
a=,
故选A.
10.如图,C、E和B、D、F分别在∠GAH的两边上,且AB=BC=CD=DE=EF,若∠A=18°,则∠GEF的度数为( )
A.75°
B.80°
C.85°
D.90°
【考点】等腰三角形的性质;三角形的外角性质.
【分析】由AB=BC=CD=DE=EF,根据等腰三角形的性质:等边对等角,可得∠ACB=∠A,∠CDB=∠CBD,∠CED=∠DCE,∠EFD=∠EDF,又由三角形外角的性质与∠A=18°,即可求得∠GEF的度数.
【解答】解:∵AB=BC,
∴∠ACB=∠A=18°,
∴∠CBD=∠A+∠ACB=36°,
∵BC=CD,
∴∠CDB=∠CBD=36°,
∴∠DCE=∠A+∠CDA=18°+36°=54°,
∵CD=DE,
∴∠CED=∠DCE=54°,
∴∠EDF=∠A+∠AED=18°+54°=72°,
∵DE=EF,
∴∠EFD=∠EDF=72°,
∴∠GEF=∠A+∠AFE=18°+72°=90°.
故选D.
11.若x=1,,则x2+4xy+4y2的值是( )
A.2
B.4
C.
D.
【考点】完全平方公式.
【分析】首先用完全平方公式将原式化简,然后再代值计算.
【解答】解:原式=(x+2y)2=(1+2×)2=4.
故选B.
12.若x2﹣3x=1,则代数式x4﹣6x3+9x2+2016的值是( )
A.2015
B.2016
C.2017
D.2018
【考点】因式分解的应用.
【分析】先将代数式进行适当的变形,然后将x2﹣3x=1代入即可求出答案.
【解答】解:∵x2﹣3x=1,
∴原式=x2(x2﹣6x+9)+2016
=x2(x﹣3)2+2016
=[x(x﹣3)]2+2016
=(x2﹣3x)2+2016
=2017
故选(C)
二、填空题(本大题有6小题,每小题4分,共24分)
13.小明从镜子里看到镜子对面电子钟的像,如图所示,实际时间是 10:51
【考点】镜面对称.
【分析】根据镜面对称的性质求解,在平面镜中的像与现实中的事物恰好左右或上下顺序颠倒,且关于镜面对称.
【解答】解:根据镜面对称的性质,分析可得题中所显示的图片与10:51成轴对称,所以此时实际时刻为10:51.故答案为10:51.
14.若点A(m+2,﹣3)与点B(4,n+5)关于x轴对称,则(mn)2= 16 .
【考点】关于x轴、y轴对称的点的坐标.
【分析】关于x轴对称的点,横坐标相同,纵坐标互为相反数
【解答】解:由题意,得
m+2=4,n+5=3,
解得m=﹣2,n=﹣2.
(mn)2=[﹣2×(﹣2)]2=16,
故答案为:16.
15.若4x2﹣2kx+1是完全平方式,则k= ±2 .
【考点】完全平方式.
【分析】这里首末两项是2x和1这两个数的平方,那么中间一项为加上或减去2x和1积的2倍.
【解答】解:∵4x2﹣2kx+1是完全平方式,
∵4x2±4x+1=(2x±1)2是完全平方式,
∴﹣2k=±4,
解得k=±2.
16.如图,在△ABC中,∠C是直角,AD平分∠BAC交BC于点D.如果AB=8,CD=2那么△ABD的面积等于 8 .
【考点】角平分线的性质;三角形的面积.
【分析】过点D作DE⊥AB,由角平分线的性质可知DE=CD=2,再根据S△ABD=AB DE即可得出结论.
【解答】解:过点D作DE⊥AB,
∵AD平分∠BAC,
∴DE=CD=2,
∴S△ABD=AB DE=×8×2=8.
故答案为:8.
17.如图,△ABC中,∠A=65°,∠B=75°,将△ABC沿EF对折,使C点与C′点重合.当∠1=45°时,∠2= 35 °.
【考点】三角形内角和定理;翻折变换(折叠问题).
【分析】由△ABC中,∠A=65°,∠B=75°,可求得∠C的度数,又由三角形内角和定理,求得∠CEF+∠CFE,继而求得∠C′EF+∠C′FE,则可求得∠1+∠2,继而求得答案.
【解答】解:∵△ABC中,∠A=65°,∠B=75°,
∴∠C=180°﹣(∠A+∠B)=40°,
∴∠CEF+∠CFE=180°﹣∠C=140°,
∵将△ABC沿EF对折,使C点与C′点重合,
∴∠C′EF+∠C′FE=∠CEF+∠CFE=140°,
∴∠1+∠2=360°﹣(∠C′EF+∠C′FE+∠CEF+∠CFE)=80°,
∵∠1=45°,
∴∠2=35°.
故答案为:35.
18.观察下列各式:
1×3+1=4=22
2×4+1=9=32
3×5+1=16=42
4×6+1=25=52
…
请你把发现的规律用含正整数n的等式表示为 n(n+2)+1=(n+1)2 .
【考点】规律型:数字的变化类.
【分析】观察不难发现,一个数前后两个数的积加上1等于这个数的平方,根据此规律写出即可.
【解答】解:∵1×3+1=4=22,
2×4+1=9=32,
3×5+1=16=42,
4×6+1=25=52,
…
∴用含正整数n的等式表示为n(n+2)+1=(n+1)2.
故答案为:n(n+2)+1=(n+1)2.
三、解答题(本大题共有7个小题,共60分)
19.分解因式:
(1)a3﹣ab2
(2)3ax2﹣6axy+3ay2.
【考点】提公因式法与公式法的综合运用.
【分析】(1)先提取公因式a,再对余下的多项式利用平方差公式继续分解;
(2)先提取公因式3a,再对余下的多项式利用完全平方公式继续分解.
【解答】解:(1)a3﹣ab2
=a(a2﹣b2)
=a(a+b)(a﹣b);
(2)3ax2﹣6axy+3ay2
=3a(x2﹣2xy+y2)
=3a(x﹣y)2.
20.计算:
(1)(3x﹣2)(2x+3)﹣(x﹣1)2;
(2)12ab2(abc)4÷(﹣3a2b3c)÷[2(abc)3].
【考点】整式的混合运算.
【分析】(1)原式第一项利用多项式乘多项式法则计算,第二项利用完全平方公式展开,去括号合并即可得到结果;
(2)原式利用幂的乘方及积的乘方运算法则计算,再利用单项式除以单项式法则计算即可得到结果.
【解答】解:(1)原式=6x2+9x﹣4x﹣6﹣x2+2x﹣1=5x2+7x﹣7;
(2)原式=12a5b6c4÷(﹣3a2b3c)÷(2a3b3c3)=﹣2c2.
21.先化简,再求值:[(x﹣2y)2﹣x(x﹣4y)﹣8xy]÷4y,其中x=﹣1,y=2.
【考点】整式的混合运算—化简求值.
【分析】原式中括号中第一项利用完全平方公式展开,第二项利用单项式乘以多项式法则计算,合并后利用多项式除以单项式法则计算得到最简结果,将x与y的值代入计算即可求出值.
【解答】解:原式=(x2﹣4xy+4y2﹣x2+4xy﹣8xy)÷4y=(4y2﹣12xy)÷4y=y﹣3x,
当x=﹣1,y=2时,原式=2+3=5.
22.在边长为1的小正方形组成的正方形网格中建立如图所示的平面直角坐标系,已知格点三角形ABC(三角形的三个顶点都在小正方形的顶点上).
(1)写出△ABC的面积: 7 .
(2)画出△ABC关于y轴对称的△A1B1C1.
(3)写出点B及其对称点B1的坐标. (﹣3,1) ; (3,1) .
【考点】作图-轴对称变换.
【分析】(1)根据图形结合坐标系可得△ABC的底AC为7,高为2,进而可得面积;
(2)首先确定A、B、C三点关于y轴的对称点位置,然后再连接即可;
(3)根据坐标系可得答案.
【解答】解:(1)2×7=7,
故答案为:7;
(2)如图所示:
(3)B(﹣3,1),B1(3,1),
故答案为:(﹣3,1);(3,1)
23.如图,在△ABC中,∠C=90°,DE垂直平分AB,分别交AB,BC于D,E.若∠CAE=∠B+30°,求∠AEB的度数.
【考点】线段垂直平分线的性质.
【分析】根据线段垂直平分线求出AE=BE,推出∠B=∠EAB,根据已知和三角形内角和定理得出∠B+30°+∠B+∠B=90°,求出∠B,即可得出答案.
【解答】解:∵DE垂直平分AB,
∴AE=BE,
∴∠B=∠EAB,
∵∠C=90°,∠CAE=∠B+30°,
∴∠B+30°+∠B+∠B=90°,
∴∠B=20°,
∴∠AEB=180°﹣20°﹣20°=140°.
24.如图,分别以△ABC的边AB、AC向外作等边△ABE和等边△ACD,直线BD与直线CE相交于点O.
(1)求证:CE=BD.
(2)如果当点A在直线BC的上方变化位置,且保持∠ABC和∠ACB都是锐角,那么∠BOC的度数是否会发生变化?若变化,请说明理由;若不变化,请求出∠BOC的度数.
【考点】全等三角形的判定与性质;等边三角形的性质.
【分析】(1)根据等边三角形的性质可得AB=AE,AC=AD,∠CAD=∠BAE=60°,再求出∠BAD=∠EAC,然后利用“边角边”证明△ABD和△AEC全等,根据全等三角形对应边相等证明即可;
(2)根据全等三角形对应角相等可得∠AEC=∠ABD,然后求出∠OEB+∠OBE=∠AEB+∠ABE,再根据三角形的一个外角等于与它不相邻的两个内角的和解答.
【解答】(1)证明:∵△ABE和△ACD都是等边三角形,
∴AB=AE,AC=AD,∠CAD=∠BAE=60°,
∵∠BAD=∠CAD+∠BAC,∠EAC=∠BAE+∠BAC,
∴∠BAD=∠EAC,
在△ABD和△AEC中,,
∴△ABD≌△AEC(SAS),
∴CE=BD;
(2)解:由(1)知,△ABD≌△AEC,
∴∠AEC=∠ABD,
又∵△ABE是等边三角形,
∴∠AEB=∠ABE=60°,
∴∠OEB+∠OBE=∠AEB+∠ABE=60°+60°=120°,
在△BOE中,∠BOC=∠OEB+∠OBE=120°,
故∠BOC的度数不会发生变化;
25.已知:三角形ABC中,∠A=90°,AB=AC,D为BC的中点,
(1)如图,E,F分别是AB,AC上的点,且BE=AF,求证:△DEF为等腰直角三角形;
(2)若E,F分别为AB,CA延长线上的点,仍有BE=AF,其他条件不变,那么,△DEF是否仍为等腰直角三角形?证明你的结论.
【考点】等腰直角三角形;全等三角形的判定与性质.
【分析】(1)先连接AD,构造全等三角形:△BED和△AFD.AD是等腰直角三角形ABC底边上的中线,所以有∠CAD=∠BAD=45°,AD=BD=CD,而∠B=∠C=45°,所以∠B=∠DAF,再加上BE=AF,AD=BD,可证出:△BED≌△AFD,从而得出DE=DF,∠BDE=∠ADF,从而得出∠EDF=90°,即△DEF是等腰直角三角形;
(2)还是证明:△BED≌△AFD,主要证∠DAF=∠DBE(∠DBE=180°﹣45°=135°,∠DAF=90°+45°=135°),再结合两组对边对应相等,所以两个三角形全等.
【解答】(1)证明:连接AD,
∵AB=AC,∠BAC=90°,D为BC的中点,
∴AD⊥BC,BD=AD.
∴∠B=∠DAC=45°
又BE=AF,
∴△BDE≌△ADF(SAS).
∴ED=FD,∠BDE=∠ADF.
∴∠EDF=∠EDA+∠ADF=∠EDA+∠BDE=∠BDA=90°.
∴△DEF为等腰直角三角形.
(2)解:△DEF为等腰直角三角形.
证明:若E,F分别是AB,CA延长线上的点,如图所示:
连接AD,
∵AB=AC,
∴△ABC为等腰三角形,
∵∠BAC=90°,D为BC的中点,
∴AD=BD,AD⊥BC(三线合一),
∴∠DAC=∠ABD=45°.
∴∠DAF=∠DBE=135°.
又AF=BE,
∴△DAF≌△DBE(SAS).
∴FD=ED,∠FDA=∠EDB.
∴∠EDF=∠EDB+∠FDB=∠FDA+∠FDB=∠ADB=90°.
∴△DEF仍为等腰直角三角形.
2017年1月27日
同课章节目录
