2017中考数学二轮复习---函数的综合应用
文档属性
| 名称 | 2017中考数学二轮复习---函数的综合应用 | 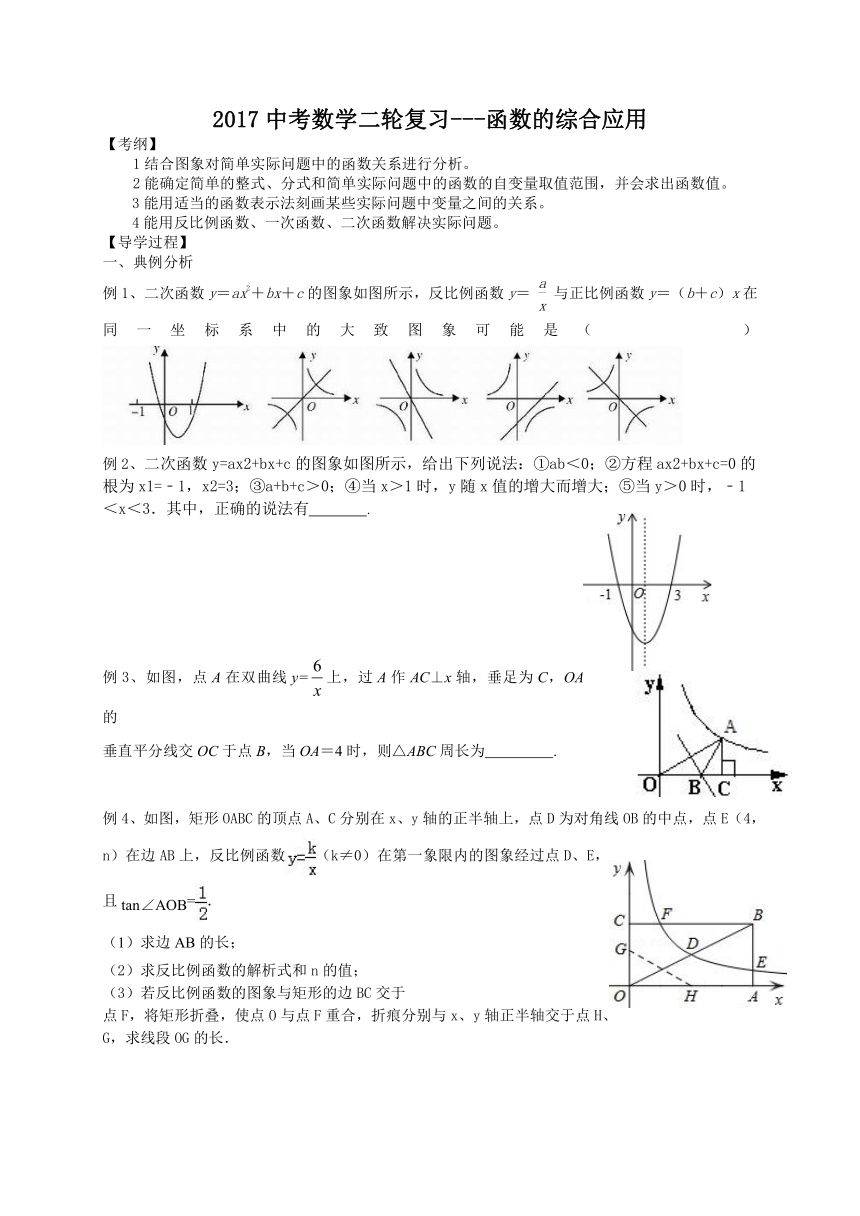 | |
| 格式 | zip | ||
| 文件大小 | 381.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-01 16:28:55 | ||
图片预览


文档简介
2017中考数学二轮复习---函数的综合应用
【考纲】
1结合图象对简单实际问题中的函数关系进行分析。
2能确定简单的整式、分式和简单实际问题中的函数的自变量取值范围,并会求出函数值。
3能用适当的函数表示法刻画某些实际问题中变量之间的关系。
4能用反比例函数、一次函数、二次函数解决实际问题。
【导学过程】
一、典例分析
例1、二次函数y=ax2+bx+c的图象如图所示,反比例函数y=
与正比例函数y=(b+c)x在同一坐标系中的大致图象可能是(
)
例2、二次函数y=ax2+bx+c的图象如图所示,给出下列说法:①ab<0;②方程ax2+bx+c=0的根为x1=﹣1,x2=3;③a+b+c>0;④当x>1时,y随x值的增大而增大;⑤当y>0时,﹣1<x<3.其中,正确的说法有
.
例3、如图,点A在双曲线y=上,过A作AC⊥x轴,垂足为C,OA的
垂直平分线交OC于点B,当OA=4时,则△ABC周长为
.
例4、如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,点E(4,n)在边AB上,反比例函数(k≠0)在第一象限内的图象经过点D、E,且tan∠AOB=.
(1)求边AB的长;
(2)求反比例函数的解析式和n的值;
(3)若反比例函数的图象与矩形的边BC交于
点F,将矩形折叠,使点O与点F重合,折痕分别与x、y轴正半轴交于点H、G,求线段OG的长.
例5、如图1,已知点A(a,0),B(0,b),且a、b满足, ABCD的边AD与y轴交于点E,且E为AD中点,双曲线经过C、D两点.
(1)求k的值;
(2)点P在双曲线上,点Q在y轴上,若以点A、B、P、Q为顶点的四边形是平行四边形,试求满足要求的所有点P、Q的坐标;
(3)以线段AB为对角线作正方形AFBH(如图3),点T是边AF上一动点,M是HT的中点,MN⊥HT,交AB于N,当T在AF上运动时,的值是否发生改变?若改变,求出其变化范围;若不改变,请求出其值,并给出你的证明.
二、基础过关
1、如图,△ABC是等腰直角三角形,∠A=90°,BC=4,点P是△BAC边上一动点,沿B→A→C的路径移动,过P点作PD⊥BC于D点,BD=x,△BDP的面积为y,则下列能大致反映y与x的函数关系的图象的是( )
2、下列图形中阴影部分的面积相等的是(
)
A.①②
B.②③
C.③④
D.①④
三、能力提升
1、如图,过点C(1,2)分别作x轴、y轴的平行线,交直线y=-x+6于A、B两点,若反比例函数(x>0)的图像与△ABC有公共点,则k的取值范围是(
)
A.2≤k≤9
B.
2≤k≤8
C.
2≤k≤5
D.
5≤k≤8
2、如图3,直角梯形AOCD的边OC在轴上,O为坐标原点,CD垂直于轴,D(5,4),AD=2.若动点同时从点O出发,点沿折线运动,到达点时停止;点沿运动,到达点时停止,它们运动的速度都是每秒1个单位长度。设运动秒时,△的面积为(平方单位)则关于的函数图象大致为( )
3、已知点A是双曲线在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为一边作等边三角形ABC,点C在第四象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为 .
4、如图,在平面直角坐标系中,点A,B坐标分别为(8,4),(0,4),点C,D在x轴上,C(t,0),D(t+3,0)(0<t≤5),过点D作x轴的垂线交线段AB于点E,交OA于点G,连接CE交OA于点F
(1)请用含t的代数式表示线段AE与EF的长;
(2)若当△EFG的面积为时,点G恰在的图象上,求k的值;
(3)若存在点Q(0,2t)与点R,其中点R在(2)中的的图象上,以A,C,Q,R为顶点的四边形是平行四边形,求R点的坐标.
5、如图,抛物线y=ax2+bx+c经过A(1,0)、B(4,0)、C(0,3)三点.
(1)求抛物线的解析式;
(2)如图①,在抛物线的对称轴上是否存在点P,使得四边形PAOC的周长最小?若存在,求出四边形PAOC周长的最小值;若不存在,请说明理由.
(3)如图②,点Q是线段OB上一动点,连接BC,在线段BC上是否存在这样的点M,使△CQM为等腰三角形且△BQM为直角三角形?若存在,求点M的坐标;若不存在,请说明理由.
【考纲】
1结合图象对简单实际问题中的函数关系进行分析。
2能确定简单的整式、分式和简单实际问题中的函数的自变量取值范围,并会求出函数值。
3能用适当的函数表示法刻画某些实际问题中变量之间的关系。
4能用反比例函数、一次函数、二次函数解决实际问题。
【导学过程】
一、典例分析
例1、二次函数y=ax2+bx+c的图象如图所示,反比例函数y=
与正比例函数y=(b+c)x在同一坐标系中的大致图象可能是(
)
例2、二次函数y=ax2+bx+c的图象如图所示,给出下列说法:①ab<0;②方程ax2+bx+c=0的根为x1=﹣1,x2=3;③a+b+c>0;④当x>1时,y随x值的增大而增大;⑤当y>0时,﹣1<x<3.其中,正确的说法有
.
例3、如图,点A在双曲线y=上,过A作AC⊥x轴,垂足为C,OA的
垂直平分线交OC于点B,当OA=4时,则△ABC周长为
.
例4、如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,点E(4,n)在边AB上,反比例函数(k≠0)在第一象限内的图象经过点D、E,且tan∠AOB=.
(1)求边AB的长;
(2)求反比例函数的解析式和n的值;
(3)若反比例函数的图象与矩形的边BC交于
点F,将矩形折叠,使点O与点F重合,折痕分别与x、y轴正半轴交于点H、G,求线段OG的长.
例5、如图1,已知点A(a,0),B(0,b),且a、b满足, ABCD的边AD与y轴交于点E,且E为AD中点,双曲线经过C、D两点.
(1)求k的值;
(2)点P在双曲线上,点Q在y轴上,若以点A、B、P、Q为顶点的四边形是平行四边形,试求满足要求的所有点P、Q的坐标;
(3)以线段AB为对角线作正方形AFBH(如图3),点T是边AF上一动点,M是HT的中点,MN⊥HT,交AB于N,当T在AF上运动时,的值是否发生改变?若改变,求出其变化范围;若不改变,请求出其值,并给出你的证明.
二、基础过关
1、如图,△ABC是等腰直角三角形,∠A=90°,BC=4,点P是△BAC边上一动点,沿B→A→C的路径移动,过P点作PD⊥BC于D点,BD=x,△BDP的面积为y,则下列能大致反映y与x的函数关系的图象的是( )
2、下列图形中阴影部分的面积相等的是(
)
A.①②
B.②③
C.③④
D.①④
三、能力提升
1、如图,过点C(1,2)分别作x轴、y轴的平行线,交直线y=-x+6于A、B两点,若反比例函数(x>0)的图像与△ABC有公共点,则k的取值范围是(
)
A.2≤k≤9
B.
2≤k≤8
C.
2≤k≤5
D.
5≤k≤8
2、如图3,直角梯形AOCD的边OC在轴上,O为坐标原点,CD垂直于轴,D(5,4),AD=2.若动点同时从点O出发,点沿折线运动,到达点时停止;点沿运动,到达点时停止,它们运动的速度都是每秒1个单位长度。设运动秒时,△的面积为(平方单位)则关于的函数图象大致为( )
3、已知点A是双曲线在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为一边作等边三角形ABC,点C在第四象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为 .
4、如图,在平面直角坐标系中,点A,B坐标分别为(8,4),(0,4),点C,D在x轴上,C(t,0),D(t+3,0)(0<t≤5),过点D作x轴的垂线交线段AB于点E,交OA于点G,连接CE交OA于点F
(1)请用含t的代数式表示线段AE与EF的长;
(2)若当△EFG的面积为时,点G恰在的图象上,求k的值;
(3)若存在点Q(0,2t)与点R,其中点R在(2)中的的图象上,以A,C,Q,R为顶点的四边形是平行四边形,求R点的坐标.
5、如图,抛物线y=ax2+bx+c经过A(1,0)、B(4,0)、C(0,3)三点.
(1)求抛物线的解析式;
(2)如图①,在抛物线的对称轴上是否存在点P,使得四边形PAOC的周长最小?若存在,求出四边形PAOC周长的最小值;若不存在,请说明理由.
(3)如图②,点Q是线段OB上一动点,连接BC,在线段BC上是否存在这样的点M,使△CQM为等腰三角形且△BQM为直角三角形?若存在,求点M的坐标;若不存在,请说明理由.
同课章节目录
