3.6比和比例课件(第1课时)(共19张PPT)
文档属性
| 名称 | 3.6比和比例课件(第1课时)(共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-03 00:00:00 | ||
图片预览






文档简介
课件19张PPT。3.6 比和比例
第1课时1.判断∶ (1)500千克∶14 吨化成最简整数比1∶125( ) ×(2)因为A×3=B×4,所以A∶B=3∶4. ( ) (3)含盐率10%的盐水中,盐和盐水的比是1∶9( ) ××(4)同一段路程,甲车行完要4小时,乙车行完要6小时,
甲、乙两车的速度比是3 ∶ 2.( ) √(5)甲、乙两个正方体棱长的比是1 ∶ 2,则它们的表
面积的比是1 ∶ 4,体积比是1 ∶ 6.( ) ×2.选择,把正确答案的序号填在括号里. (1)有一天,某班的出勤率是90%,出勤人数和缺勤人
数的比是( )
①9∶10 ②10∶9 ③1∶9 ④9∶1 ④(2)用3、5、9、15这四个数组成的比例式是( )
①15∶3=5∶9 ②3∶15=9∶5
③15∶9=5∶3 ④9∶3=5∶15 ③(3)大、小两圆半径的比是3∶2,它们的周长之比是( ),
面积之比是( ).
①3∶2 ②6∶4 ③9∶4 ①③3.化简比14 ∶21= ∶=1.25∶2=2 ∶ 33∶45∶8(比的前项和后项同时除以它们的最大公约数.)(一般先把比的前项、后项同时乘上分母的最小公
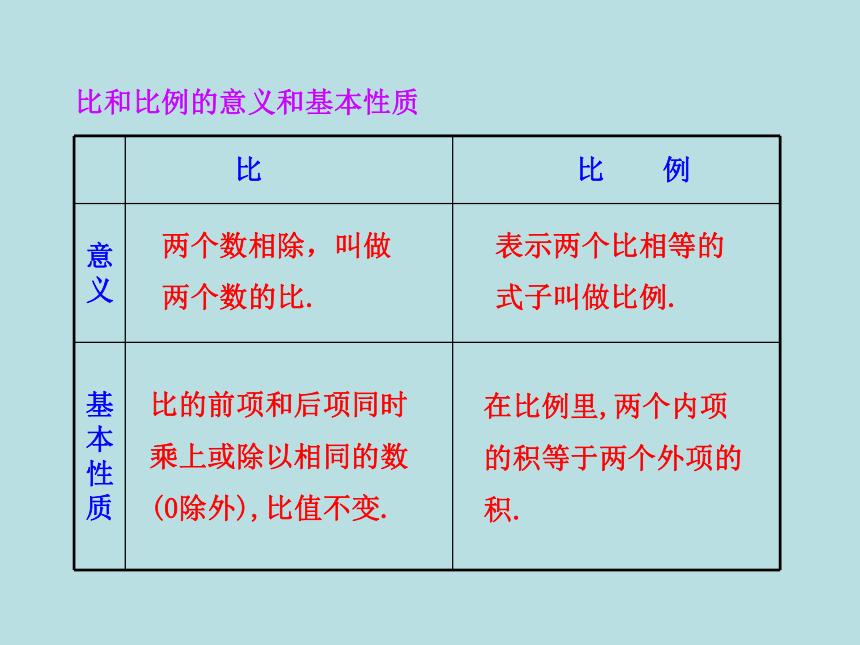
倍数,使它成为整数比,再化简)(一般是把前项、后项的小数点向右移动相同的位数,使它成为整数比,再化简)比和比例的意义和基本性质表示两个比相等的式子叫做比例.两个数相除,叫做两个数的比.比的前项和后项同时乘上或除以相同的数(0除外),比值不变.在比例里,两个内项的积等于两个外项的积.求比值和化简比的区别根据比值的意义,用前项除以后项.是一个商,可以是整数、小数或分数.根据比的基本性质,把比的前项和后项同时乘上或除以相同的数(0除外).是一个比,它的前项和后项都是整数.1.理解比例的意义,认识比例各部分名称,初步了解比和
比例的区别;理解比例的基本性质.
2.能根据比例的意义和基本性质,正确判断两个比能否组
成比例.
3.在自主探究、观察比较中,培养学生分析、概括能力和
勇于探索的精神. 两个数a与b(b≠0)相除,叫做a与b的比,记作a:b,其中a叫做比的前项,b叫做比的后项.表示两个比相等的式子叫做比例式,简称比例.
如果a与b的比等于c与d的比,就说a、b、c、d四个数成
比例.可以写成a:b=c:d
在比例中,a,b,c,d叫做组成比例的项,其中a与d叫
做比例的外项,b与c叫做比例的内项.
当比例的两个内项相等,即a:b=b:c时,b叫做a和c的比
例中项.比例的各部分名称是怎么规定的?18 ︰ 15 = 24 ︰ 20 内项 外项请指出下列比例的两个外项和内项各是多少?①6 ∶ 10=9 ∶ 15 ???? ②?0.2 ∶ 2.5=4 ∶ 50
③2.4 ∶ 1.6=60 ∶ 40 学校航模组有男生18人,女生15人;美术组有男生24人,女生20人.航模组男、女生人数的比和美术组男、女生人数的比能组成比例吗?即如果a∶b=c∶d,
那么ad=bc或bc=ad(bd ≠0)每个比例的两个外项和两个内项之间存在有什么共同的特
点么? ①6 ∶ 10=9∶15 ??? ②?0.2∶2.5=4∶50
③2.4∶1.6=60∶40 比例的基本性质∶在比例中,两个外项的积等于两个内项
的积(1)2a=3b?
(2)解析∶(1)由2a=3b,得 ,所以a∶b=3∶2
(2)由 ,可得2(a-b)=a,从而a=2b,
所以a∶b=2∶1=2【例 题】例1 根据下列各题的条件,求a∶b的值如果三个数进行比怎么办?甲、乙、丙三人合伙经营水果,去年年底按投资的比例
进行分红,甲分红5万元,乙分红4万元,丙分红3万元.
思考下面的问题
1)甲的分红∶乙的分红=_________;
乙的分红∶丙的分红=_________.
2)按照上面的结果,可以把甲、乙、丙三人的
分红的比写成
甲的分红∶乙的分红∶丙的分红=__∶__∶__.这种形式叫做连比5 4 35∶44∶3例2 ①已知a∶b=2∶3,b∶c=3∶5,求a∶b∶c
②已知a∶b=2∶3,b∶c=4∶5,求a∶b∶c解析∶①因为a∶b=2∶3,b∶c=3∶5,
所以a∶b∶c=2∶3∶5②a∶b=2∶3=(2×4)∶(3×4)=8∶12b∶c=4∶5=(4×3)∶(5×3)=12∶15所以a ∶ b ∶ c=8 ∶ 12 ∶ 15【例 题】根据下列条件,求x∶y∶z
① 已知x∶y=3∶4,y∶z=4∶7;
② x∶y=3∶4,y∶z=6∶7. 解析∶① x∶y=3∶4,y∶z=4∶7,
所以x∶y∶z=3∶4∶7
② x∶y=3∶4=9∶12,y∶z=6∶7=12∶14.
所以x∶y∶z=9∶ 12∶14【跟踪训练】通过本课时的学习,需要我们掌握∶1.比例及比例式的相关概念.
2.比例的基本性质∶
在比例中,两个外项的积等于两个内项的积1.把下列各连比化为最简整数比.
(1)80∶120∶160;??
(2)0.2∶0.4∶0.6解析∶(1) 80∶120∶160=2∶3∶4
(2)0.2∶0.4∶0.6=2∶4∶6=1∶2∶32.某工厂有三种主要产品的年产值分别是1250万元、
950万元、150万元.求这三种产品的年产值的比.解析:1250∶950∶150=25∶19∶3
答:这三种产品的年产值的比为25∶19∶33.已知
求 的值.解析∶设 =k,则x=3k,y=4k,z=6k.
第1课时1.判断∶ (1)500千克∶14 吨化成最简整数比1∶125( ) ×(2)因为A×3=B×4,所以A∶B=3∶4. ( ) (3)含盐率10%的盐水中,盐和盐水的比是1∶9( ) ××(4)同一段路程,甲车行完要4小时,乙车行完要6小时,
甲、乙两车的速度比是3 ∶ 2.( ) √(5)甲、乙两个正方体棱长的比是1 ∶ 2,则它们的表
面积的比是1 ∶ 4,体积比是1 ∶ 6.( ) ×2.选择,把正确答案的序号填在括号里. (1)有一天,某班的出勤率是90%,出勤人数和缺勤人
数的比是( )
①9∶10 ②10∶9 ③1∶9 ④9∶1 ④(2)用3、5、9、15这四个数组成的比例式是( )
①15∶3=5∶9 ②3∶15=9∶5
③15∶9=5∶3 ④9∶3=5∶15 ③(3)大、小两圆半径的比是3∶2,它们的周长之比是( ),
面积之比是( ).
①3∶2 ②6∶4 ③9∶4 ①③3.化简比14 ∶21= ∶=1.25∶2=2 ∶ 33∶45∶8(比的前项和后项同时除以它们的最大公约数.)(一般先把比的前项、后项同时乘上分母的最小公
倍数,使它成为整数比,再化简)(一般是把前项、后项的小数点向右移动相同的位数,使它成为整数比,再化简)比和比例的意义和基本性质表示两个比相等的式子叫做比例.两个数相除,叫做两个数的比.比的前项和后项同时乘上或除以相同的数(0除外),比值不变.在比例里,两个内项的积等于两个外项的积.求比值和化简比的区别根据比值的意义,用前项除以后项.是一个商,可以是整数、小数或分数.根据比的基本性质,把比的前项和后项同时乘上或除以相同的数(0除外).是一个比,它的前项和后项都是整数.1.理解比例的意义,认识比例各部分名称,初步了解比和
比例的区别;理解比例的基本性质.
2.能根据比例的意义和基本性质,正确判断两个比能否组
成比例.
3.在自主探究、观察比较中,培养学生分析、概括能力和
勇于探索的精神. 两个数a与b(b≠0)相除,叫做a与b的比,记作a:b,其中a叫做比的前项,b叫做比的后项.表示两个比相等的式子叫做比例式,简称比例.
如果a与b的比等于c与d的比,就说a、b、c、d四个数成
比例.可以写成a:b=c:d
在比例中,a,b,c,d叫做组成比例的项,其中a与d叫
做比例的外项,b与c叫做比例的内项.
当比例的两个内项相等,即a:b=b:c时,b叫做a和c的比
例中项.比例的各部分名称是怎么规定的?18 ︰ 15 = 24 ︰ 20 内项 外项请指出下列比例的两个外项和内项各是多少?①6 ∶ 10=9 ∶ 15 ???? ②?0.2 ∶ 2.5=4 ∶ 50
③2.4 ∶ 1.6=60 ∶ 40 学校航模组有男生18人,女生15人;美术组有男生24人,女生20人.航模组男、女生人数的比和美术组男、女生人数的比能组成比例吗?即如果a∶b=c∶d,
那么ad=bc或bc=ad(bd ≠0)每个比例的两个外项和两个内项之间存在有什么共同的特
点么? ①6 ∶ 10=9∶15 ??? ②?0.2∶2.5=4∶50
③2.4∶1.6=60∶40 比例的基本性质∶在比例中,两个外项的积等于两个内项
的积(1)2a=3b?
(2)解析∶(1)由2a=3b,得 ,所以a∶b=3∶2
(2)由 ,可得2(a-b)=a,从而a=2b,
所以a∶b=2∶1=2【例 题】例1 根据下列各题的条件,求a∶b的值如果三个数进行比怎么办?甲、乙、丙三人合伙经营水果,去年年底按投资的比例
进行分红,甲分红5万元,乙分红4万元,丙分红3万元.
思考下面的问题
1)甲的分红∶乙的分红=_________;
乙的分红∶丙的分红=_________.
2)按照上面的结果,可以把甲、乙、丙三人的
分红的比写成
甲的分红∶乙的分红∶丙的分红=__∶__∶__.这种形式叫做连比5 4 35∶44∶3例2 ①已知a∶b=2∶3,b∶c=3∶5,求a∶b∶c
②已知a∶b=2∶3,b∶c=4∶5,求a∶b∶c解析∶①因为a∶b=2∶3,b∶c=3∶5,
所以a∶b∶c=2∶3∶5②a∶b=2∶3=(2×4)∶(3×4)=8∶12b∶c=4∶5=(4×3)∶(5×3)=12∶15所以a ∶ b ∶ c=8 ∶ 12 ∶ 15【例 题】根据下列条件,求x∶y∶z
① 已知x∶y=3∶4,y∶z=4∶7;
② x∶y=3∶4,y∶z=6∶7. 解析∶① x∶y=3∶4,y∶z=4∶7,
所以x∶y∶z=3∶4∶7
② x∶y=3∶4=9∶12,y∶z=6∶7=12∶14.
所以x∶y∶z=9∶ 12∶14【跟踪训练】通过本课时的学习,需要我们掌握∶1.比例及比例式的相关概念.
2.比例的基本性质∶
在比例中,两个外项的积等于两个内项的积1.把下列各连比化为最简整数比.
(1)80∶120∶160;??
(2)0.2∶0.4∶0.6解析∶(1) 80∶120∶160=2∶3∶4
(2)0.2∶0.4∶0.6=2∶4∶6=1∶2∶32.某工厂有三种主要产品的年产值分别是1250万元、
950万元、150万元.求这三种产品的年产值的比.解析:1250∶950∶150=25∶19∶3
答:这三种产品的年产值的比为25∶19∶33.已知
求 的值.解析∶设 =k,则x=3k,y=4k,z=6k.
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
