【冀教版】2017年春九下数学:29.3《切线的性质和判定》课件
文档属性
| 名称 | 【冀教版】2017年春九下数学:29.3《切线的性质和判定》课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-07 00:00:00 | ||
图片预览



文档简介
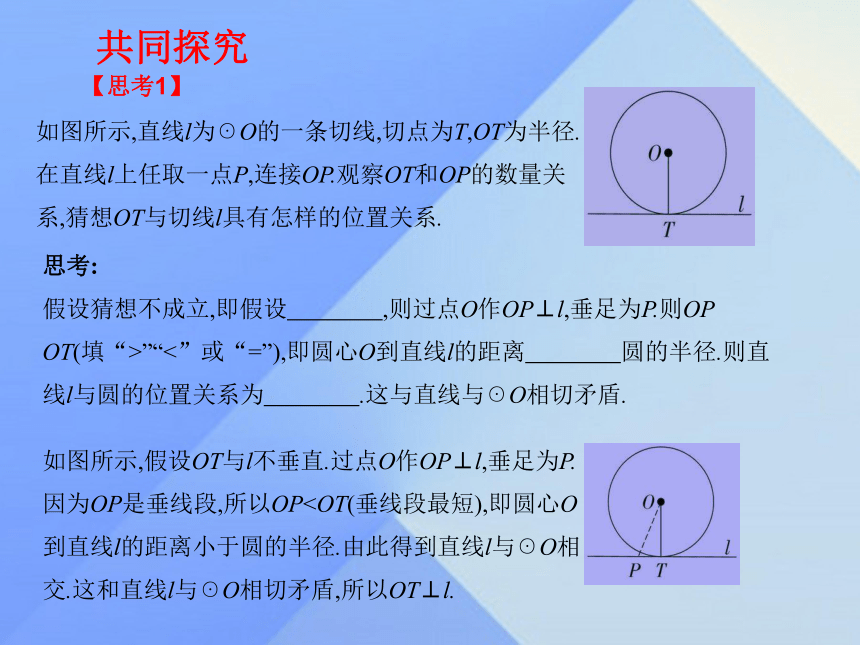
课件10张PPT。九年级数学·下 新课标[冀教]第二十九章 直线与圆的位置关系29.3 切线的性质和判定1.下雨天,当你转动雨伞,你会发现雨伞上的水珠顺着伞面的边缘飞出.仔细观察一下,水珠是顺着什么样的方向飞出的?这就是我们所要研究的直线与圆相切的情况.2.在我们的生活中,经常会遇到直线与圆相切的情形.如沿直线行驶的自行车车轮与车印,可以看成直线与圆相切的具体实例.共同探究【思考1】 如图所示,直线l为☉O的一条切线,切点为T,OT为半径.在直线l上任取一点P,连接OP.观察OT和OP的数量关系,猜想OT与切线l具有怎样的位置关系.思考:
假设猜想不成立,即假设 ,则过点O作OP⊥l,垂足为P.则OP OT(填“>”“<”或“=”),即圆心O到直线l的距离 圆的半径.则直线l与圆的位置关系为 .这与直线与☉O相切矛盾.?如图所示,假设OT与l不垂直.过点O作OP⊥l,垂足为P.因为OP是垂线段,所以OP2.如何用几何语言表示你得出的结论?【思考2】 性质:圆的切线垂直于过切点的半径.
几何语言:如图所示,∵直线l切☉O于T,
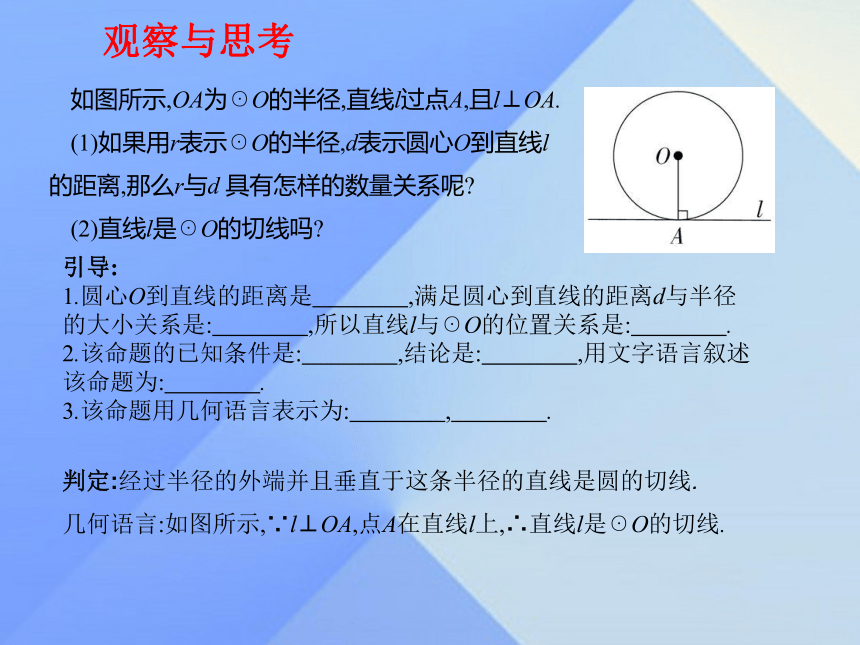
∴OT⊥l.观察与思考如图所示,OA为☉O的半径,直线l过点A,且l⊥OA.
(1)如果用r表示☉O的半径,d表示圆心O到直线l的距离,那么r与d 具有怎样的数量关系呢?
(2)直线l是☉O的切线吗?引导:
1.圆心O到直线的距离是 ,满足圆心到直线的距离d与半径的大小关系是: ,所以直线l与☉O的位置关系是: .?
2.该命题的已知条件是: ,结论是: ,用文字语言叙述该命题为: .?
3.该命题用几何语言表示为: , .?判定:经过半径的外端并且垂直于这条半径的直线是圆的切线.
几何语言:如图所示,∵l⊥OA,点A在直线l上,∴直线l是☉O的切线.追加思考:
1.你如何证明一条直线是圆的切线?
2.你能举出生活中直线与圆相切的实例吗?(直线与圆只有一个公共点;圆心到直线的距离等于半径;经过半径的外端并且垂直于这条半径的直线.)做一做如图所示,P为☉O上的一点,请你用三角尺画出这个圆经过点P的切线.思考:
过点P的切线与半径OP有怎样的位置关系?(过点P的切线与半径OP垂直.)先连接OP,再过点P作直线l⊥OP,直线l就是过点P的切线.1.利用切线的判定定理需要满足两个条件:(1)经过半径的外端;(2)与半径垂直.两个条件缺一不可,否则不一定是切线.如下图所示,这里的直线l都不是☉O的切线.[知识拓展]2.判定一条直线是圆的切线的方法:(1)若直线与圆只有一个公共点,则该直线是圆的切线;(2)若圆心到直线的距离等于半径,则该直线是圆的切线;(3)经过半径的外端并且垂直于这条半径的直线是圆的切线.3.利用切线的判定定理进行证明时,当直线和圆有公共点时,连接过公共点的半径,然后证明直线垂直于这条半径,简称“作半径,证垂直”;当直线与圆的公共点不明确时,可过圆心作直线的垂线,再证明圆心到直线的距离等于圆的半径,简称“作垂直,证半径”.1.(2016·长春中考)如图所示,PA,PB是☉O的切线,切点分别为A,B.若OA=2,∠P=60°,则 的长为( )
A. π B. π C. π D. π解析:由切线的性质可得∠PBO=∠PAO=90°,又四边形的内角和为360°,所以∠AOB=120°,由弧长公式可得 的长为 故选C.C2.如图所示,若☉O的直径AB与弦AC的夹角为30°,切线CD与AB的延长线交于点D,且☉O的半径为2,则CD的长为 ( )
A.2 B.4
C.2 D.4解析:连接OC.∵CD是圆的切线,
∴∠OCD=90°.∵OA=OC,∴∠ACO=∠A=30°,
∴∠COD=∠A+∠ACO=60°,∴∠D=30°.又OC=2,∴OD=2OC=4,∴CD= .故选A.A3.如图所示,从☉O外一点A引圆的切线AB,切点为B,连接AO并延长交圆于点C,连接BC,若∠A=26°,则∠ACB= .?解析:连接OB,易得OB⊥AB,由∠A=26°,得∠AOB=64°,从而求得∠ACB=32°.故填32°.32°4.如图所示,线段AB经过圆心O,交☉O于A,C两点,∠BAD=∠B=30°,直线BD交☉O于点D.
(1)BD是☉O的切线吗?为什么?
(2)若AC=10,求线段BD的长度.解:(1)BD是☉O的切线.
理由:∵∠BAD=∠B=30°,
∴∠ADB=180°-30°-30°=120°.
∵AO=DO,∴∠A=∠ADO=30°,
∴∠ODB=120°-30°=90°,
∴BD是☉O的切线.(2)∵AC=10,∴CO=5,∴DO=5.
∵∠B=30°,由(1)知∠ODB=90°,∴BO=2DO=10.
在Rt△OBD中,
BD=
假设猜想不成立,即假设 ,则过点O作OP⊥l,垂足为P.则OP OT(填“>”“<”或“=”),即圆心O到直线l的距离 圆的半径.则直线l与圆的位置关系为 .这与直线与☉O相切矛盾.?如图所示,假设OT与l不垂直.过点O作OP⊥l,垂足为P.因为OP是垂线段,所以OP
几何语言:如图所示,∵直线l切☉O于T,
∴OT⊥l.观察与思考如图所示,OA为☉O的半径,直线l过点A,且l⊥OA.
(1)如果用r表示☉O的半径,d表示圆心O到直线l的距离,那么r与d 具有怎样的数量关系呢?
(2)直线l是☉O的切线吗?引导:
1.圆心O到直线的距离是 ,满足圆心到直线的距离d与半径的大小关系是: ,所以直线l与☉O的位置关系是: .?
2.该命题的已知条件是: ,结论是: ,用文字语言叙述该命题为: .?
3.该命题用几何语言表示为: , .?判定:经过半径的外端并且垂直于这条半径的直线是圆的切线.
几何语言:如图所示,∵l⊥OA,点A在直线l上,∴直线l是☉O的切线.追加思考:
1.你如何证明一条直线是圆的切线?
2.你能举出生活中直线与圆相切的实例吗?(直线与圆只有一个公共点;圆心到直线的距离等于半径;经过半径的外端并且垂直于这条半径的直线.)做一做如图所示,P为☉O上的一点,请你用三角尺画出这个圆经过点P的切线.思考:
过点P的切线与半径OP有怎样的位置关系?(过点P的切线与半径OP垂直.)先连接OP,再过点P作直线l⊥OP,直线l就是过点P的切线.1.利用切线的判定定理需要满足两个条件:(1)经过半径的外端;(2)与半径垂直.两个条件缺一不可,否则不一定是切线.如下图所示,这里的直线l都不是☉O的切线.[知识拓展]2.判定一条直线是圆的切线的方法:(1)若直线与圆只有一个公共点,则该直线是圆的切线;(2)若圆心到直线的距离等于半径,则该直线是圆的切线;(3)经过半径的外端并且垂直于这条半径的直线是圆的切线.3.利用切线的判定定理进行证明时,当直线和圆有公共点时,连接过公共点的半径,然后证明直线垂直于这条半径,简称“作半径,证垂直”;当直线与圆的公共点不明确时,可过圆心作直线的垂线,再证明圆心到直线的距离等于圆的半径,简称“作垂直,证半径”.1.(2016·长春中考)如图所示,PA,PB是☉O的切线,切点分别为A,B.若OA=2,∠P=60°,则 的长为( )
A. π B. π C. π D. π解析:由切线的性质可得∠PBO=∠PAO=90°,又四边形的内角和为360°,所以∠AOB=120°,由弧长公式可得 的长为 故选C.C2.如图所示,若☉O的直径AB与弦AC的夹角为30°,切线CD与AB的延长线交于点D,且☉O的半径为2,则CD的长为 ( )
A.2 B.4
C.2 D.4解析:连接OC.∵CD是圆的切线,
∴∠OCD=90°.∵OA=OC,∴∠ACO=∠A=30°,
∴∠COD=∠A+∠ACO=60°,∴∠D=30°.又OC=2,∴OD=2OC=4,∴CD= .故选A.A3.如图所示,从☉O外一点A引圆的切线AB,切点为B,连接AO并延长交圆于点C,连接BC,若∠A=26°,则∠ACB= .?解析:连接OB,易得OB⊥AB,由∠A=26°,得∠AOB=64°,从而求得∠ACB=32°.故填32°.32°4.如图所示,线段AB经过圆心O,交☉O于A,C两点,∠BAD=∠B=30°,直线BD交☉O于点D.
(1)BD是☉O的切线吗?为什么?
(2)若AC=10,求线段BD的长度.解:(1)BD是☉O的切线.
理由:∵∠BAD=∠B=30°,
∴∠ADB=180°-30°-30°=120°.
∵AO=DO,∴∠A=∠ADO=30°,
∴∠ODB=120°-30°=90°,
∴BD是☉O的切线.(2)∵AC=10,∴CO=5,∴DO=5.
∵∠B=30°,由(1)知∠ODB=90°,∴BO=2DO=10.
在Rt△OBD中,
BD=
