【冀教版】2017年春九下数学:29.4《切线长定理》课件
文档属性
| 名称 | 【冀教版】2017年春九下数学:29.4《切线长定理》课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-07 13:35:06 | ||
图片预览




文档简介
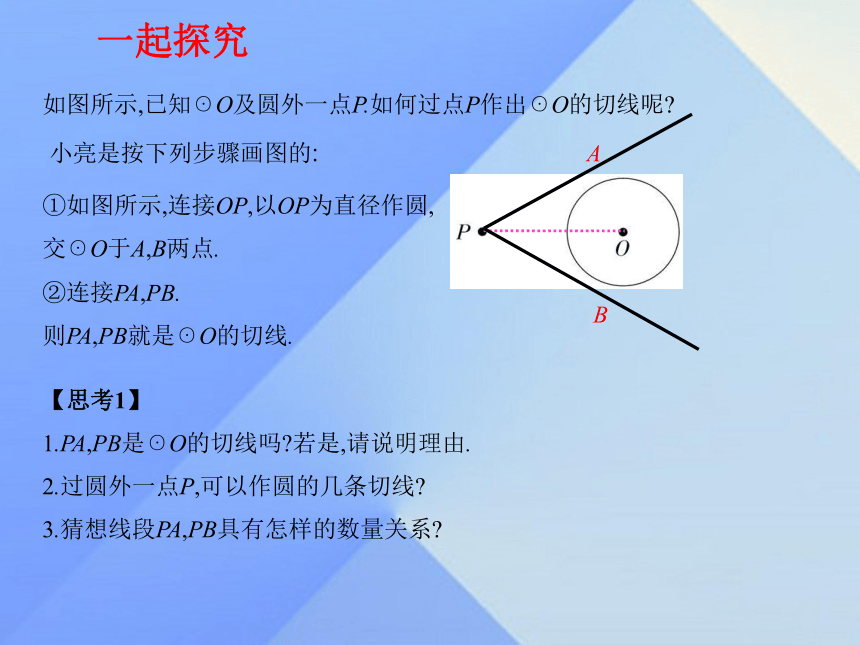
课件11张PPT。九年级数学·下 新课标[冀教]第二十九章 直线与圆的位置关系29.4 切线长定理如图所示,小明同学测量一个光盘的直径,他将直尺、光盘和三角尺置于桌面上,如果量出AB的长度,就可以求此光盘的直径,你能说出怎样求出光盘的直径吗?一起探究如图所示,已知☉O及圆外一点P.如何过点P作出☉O的切线呢?小亮是按下列步骤画图的:①如图所示,连接OP,以OP为直径作圆,交☉O于A,B两点.AB②连接PA,PB.
则PA,PB就是☉O的切线.【思考1】
1.PA,PB是☉O的切线吗?若是,请说明理由.
2.过圆外一点P,可以作圆的几条切线?
3.猜想线段PA,PB具有怎样的数量关系?4.完成下面的证明过程.已知:如图所示,P是☉O外一点,PA,PB分别与☉O相切于点A,B.
求证PA=PB.证明:如图所示,连接OA,OB,OP.在Rt△OAP和Rt△OBP中,
∵PA,PB分别与☉O相切于点A,B,
∴PA⊥OA,PB⊥OB.
∴∠OAP=∠OBP=90°.又∵OA=OB,OP=OP,
∴Rt△OAP≌Rt△OBP.
∴PA=PB.切线长:我们把线段PA,PB的长叫做点P到☉O的切线长.【思考2】
切线与切线长有什么区别?(切线是直线,无法度量;切线长是切线上一条线段的长,即圆外一点与切点之间的距离,可以度量.)【思考3】
1.你能用语言叙述上述结论吗?
2.在上图中还有其他的结论成立吗?若连接AB,你又能得到哪些结论?切线长定理:过圆外一点所画的圆的两条切线的切线长相等.
上图中的结论还有:∠APO=∠BPO= ∠APB,∠AOP=∠BOP= ∠AOB,∠OAP=∠OBP=90°,∠BOA+∠APB=180°.若连接AB,则有PO垂直平分AB等结论.(教材第12页例1)已知:如图所示,过点P的两条直线分别与☉O相切于点A,B,Q为劣弧 上异于点A,B的任意一点,过点Q的切线分别与切线PA,PB相交于点C,D.
求证△PCD的周长等于2PA.证明:∵PA,PB,CD都是☉O的切线,
∴PA=PB,CQ=CA,DQ=DB.∴△PCD的周长=PC+PD+CD
=PC+PD+CQ+DQ
=PC+PD+CA+DB
=PA+PB=2PA.(教材第12页例2)用尺规作圆,使其与已知三角形的三边都相切.已知:如图所示,△ABC.
求作:☉I,使它与△ABC的三边都相切.分析:1.作圆的关键是什么?
2.如果☉I与△ABC的三边都相切,那么圆心I到三边的距离有什么等量关系?
3.三角形三条角平分线的交点有什么性质?
4.圆心I与三角形三条角平分线的交点有什么关系?
5.找到圆心后,如何确定圆的半径?(找圆心和半径)(圆心I到三边的距离相等)(到三角形三边的距离相等)(圆心I为三角形三条角平分线的交点)(圆心到三边的距离相等,且为半径)作法:如图所示.(1)分别作∠B和∠C的平分线BM和CN.设BM与CN交于点I.(2)过点I作ID⊥BC,垂足为D.(3)以点I为圆心、ID的长为半径作☉I,☉I即为所求.内切圆:与三角形的三边都相切的圆有且只有一个,我们称这个圆为三角形的内切圆.
内心:内切圆的圆心是三角形三条角平分线的交点,叫做三角形的内心.MNID1.如图所示,PA切☉O于点A,PB切☉O于点B,OP交☉O于点C,下列结论中错误的是 ( )
A.∠APO=∠BPO B.PA=PB
C.AB⊥OP D.C是PO的中点解析:根据切线长定理可得∠APO=∠BPO,PA=PB,AB⊥OP都成立,只有D不正确.故选D.D2.如图所示,从圆外一点P引☉O的两条切线PA,PB,切点分别为A,B,若∠APB=60°,PA=10,则弦AB的长为 ( )
A.5 B. 5 C.10 D. 10 解析:∵PA,PB都是☉O的切线,∴PA=PB.∵∠APB=60°,∴△PAB是等边三角形.∵PA=10,∴AB=10.故选C.C3.如图所示,PA,PB分别切☉O于A,B两点,并与☉O的切线分别相交于C,D两点,已知PA=7 cm,则△PCD的周长等于 .?解析:设DC与☉O的切点为E,∵PA,PB分别是☉O的切线,且切点为A,B,∴PA=PB=7 cm.同理可得DE=DA,CE=CB,即△PCD的周长=PD+DE+CE+PC=PD+DA+PC+CB=PA+PB=14(cm).故填14 cm.14 cm.4.在△ABC中,∠A=50°,I是△ABC的内心,则∠BIC= .?解析:∵IB,IC分别是∠ABC,∠ACB的平分线,∴∠IBC+∠ICB= (∠ABC+∠ACB)= (180°-50°)=65°,∴∠BIC=180°-65°=115°.故填115°.115°5.如图所示,已知AB为☉O的直径,PA,PC是☉O的切线,
A,C为切点,∠BAC=30°.
(1)求∠P的大小;
(2)若AB=2,求PA的长(结果保留根号).解:(1)∵PA是☉O的切线,AB为☉O的直径,
∴PA⊥AB,∴∠BAP=90°.
∵∠BAC=30°,
∴∠CAP=90°-∠BAC=60°.
又∵PA,PC分别切☉O于点A,C,
∴PA=PC,∴△PAC为等边三角形,
∴∠P=60°.(2)如图所示,连接BC,
∵AB是☉O的直径,
∴∠ACB=90°.
在Rt△ACB中,AB=2,∠BAC=30°,
∴BC= AB=1,∴AC=
∵△PAC为等边三角形,
∴PA=AC,∴PA=
则PA,PB就是☉O的切线.【思考1】
1.PA,PB是☉O的切线吗?若是,请说明理由.
2.过圆外一点P,可以作圆的几条切线?
3.猜想线段PA,PB具有怎样的数量关系?4.完成下面的证明过程.已知:如图所示,P是☉O外一点,PA,PB分别与☉O相切于点A,B.
求证PA=PB.证明:如图所示,连接OA,OB,OP.在Rt△OAP和Rt△OBP中,
∵PA,PB分别与☉O相切于点A,B,
∴PA⊥OA,PB⊥OB.
∴∠OAP=∠OBP=90°.又∵OA=OB,OP=OP,
∴Rt△OAP≌Rt△OBP.
∴PA=PB.切线长:我们把线段PA,PB的长叫做点P到☉O的切线长.【思考2】
切线与切线长有什么区别?(切线是直线,无法度量;切线长是切线上一条线段的长,即圆外一点与切点之间的距离,可以度量.)【思考3】
1.你能用语言叙述上述结论吗?
2.在上图中还有其他的结论成立吗?若连接AB,你又能得到哪些结论?切线长定理:过圆外一点所画的圆的两条切线的切线长相等.
上图中的结论还有:∠APO=∠BPO= ∠APB,∠AOP=∠BOP= ∠AOB,∠OAP=∠OBP=90°,∠BOA+∠APB=180°.若连接AB,则有PO垂直平分AB等结论.(教材第12页例1)已知:如图所示,过点P的两条直线分别与☉O相切于点A,B,Q为劣弧 上异于点A,B的任意一点,过点Q的切线分别与切线PA,PB相交于点C,D.
求证△PCD的周长等于2PA.证明:∵PA,PB,CD都是☉O的切线,
∴PA=PB,CQ=CA,DQ=DB.∴△PCD的周长=PC+PD+CD
=PC+PD+CQ+DQ
=PC+PD+CA+DB
=PA+PB=2PA.(教材第12页例2)用尺规作圆,使其与已知三角形的三边都相切.已知:如图所示,△ABC.
求作:☉I,使它与△ABC的三边都相切.分析:1.作圆的关键是什么?
2.如果☉I与△ABC的三边都相切,那么圆心I到三边的距离有什么等量关系?
3.三角形三条角平分线的交点有什么性质?
4.圆心I与三角形三条角平分线的交点有什么关系?
5.找到圆心后,如何确定圆的半径?(找圆心和半径)(圆心I到三边的距离相等)(到三角形三边的距离相等)(圆心I为三角形三条角平分线的交点)(圆心到三边的距离相等,且为半径)作法:如图所示.(1)分别作∠B和∠C的平分线BM和CN.设BM与CN交于点I.(2)过点I作ID⊥BC,垂足为D.(3)以点I为圆心、ID的长为半径作☉I,☉I即为所求.内切圆:与三角形的三边都相切的圆有且只有一个,我们称这个圆为三角形的内切圆.
内心:内切圆的圆心是三角形三条角平分线的交点,叫做三角形的内心.MNID1.如图所示,PA切☉O于点A,PB切☉O于点B,OP交☉O于点C,下列结论中错误的是 ( )
A.∠APO=∠BPO B.PA=PB
C.AB⊥OP D.C是PO的中点解析:根据切线长定理可得∠APO=∠BPO,PA=PB,AB⊥OP都成立,只有D不正确.故选D.D2.如图所示,从圆外一点P引☉O的两条切线PA,PB,切点分别为A,B,若∠APB=60°,PA=10,则弦AB的长为 ( )
A.5 B. 5 C.10 D. 10 解析:∵PA,PB都是☉O的切线,∴PA=PB.∵∠APB=60°,∴△PAB是等边三角形.∵PA=10,∴AB=10.故选C.C3.如图所示,PA,PB分别切☉O于A,B两点,并与☉O的切线分别相交于C,D两点,已知PA=7 cm,则△PCD的周长等于 .?解析:设DC与☉O的切点为E,∵PA,PB分别是☉O的切线,且切点为A,B,∴PA=PB=7 cm.同理可得DE=DA,CE=CB,即△PCD的周长=PD+DE+CE+PC=PD+DA+PC+CB=PA+PB=14(cm).故填14 cm.14 cm.4.在△ABC中,∠A=50°,I是△ABC的内心,则∠BIC= .?解析:∵IB,IC分别是∠ABC,∠ACB的平分线,∴∠IBC+∠ICB= (∠ABC+∠ACB)= (180°-50°)=65°,∴∠BIC=180°-65°=115°.故填115°.115°5.如图所示,已知AB为☉O的直径,PA,PC是☉O的切线,
A,C为切点,∠BAC=30°.
(1)求∠P的大小;
(2)若AB=2,求PA的长(结果保留根号).解:(1)∵PA是☉O的切线,AB为☉O的直径,
∴PA⊥AB,∴∠BAP=90°.
∵∠BAC=30°,
∴∠CAP=90°-∠BAC=60°.
又∵PA,PC分别切☉O于点A,C,
∴PA=PC,∴△PAC为等边三角形,
∴∠P=60°.(2)如图所示,连接BC,
∵AB是☉O的直径,
∴∠ACB=90°.
在Rt△ACB中,AB=2,∠BAC=30°,
∴BC= AB=1,∴AC=
∵△PAC为等边三角形,
∴PA=AC,∴PA=
