【冀教版】2017年春九下数学:30.2《二次函数的图象和性质(2)》课件
文档属性
| 名称 | 【冀教版】2017年春九下数学:30.2《二次函数的图象和性质(2)》课件 |  | |
| 格式 | zip | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-07 13:33:47 | ||
图片预览






文档简介
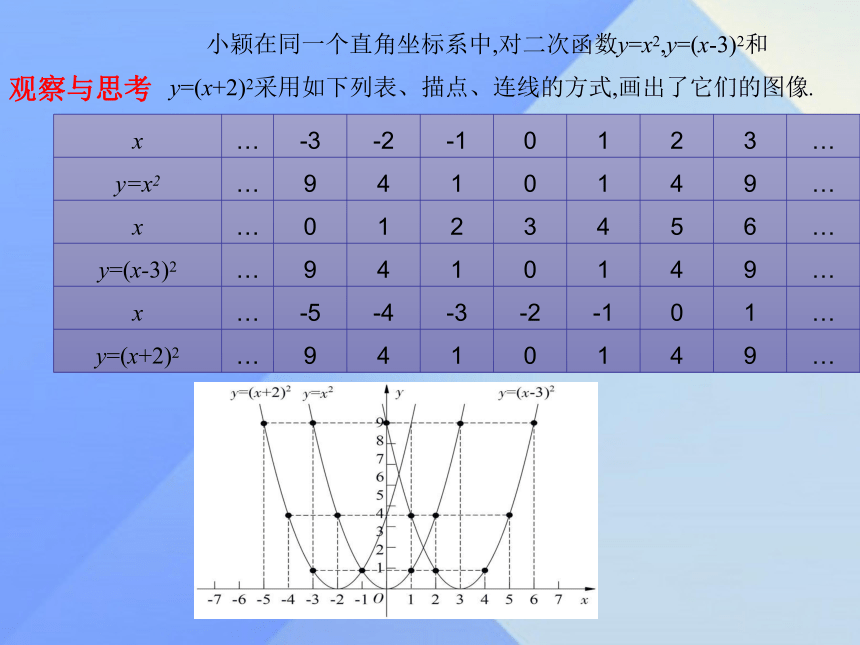
课件14张PPT。九年级数学·下 新课标[冀教]第三十章 二次函数30.2 二次函数的图象和性质(第2课时)学 习 新 知 要修建一个圆形喷水池,在池中心竖直安装一根水管,在水管的顶端安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为1 m处达到最高,高度为3 m,水柱落地处与池中心的水平距离为3 m,水管应多长?观察与思考 小颖在同一个直角坐标系中,对二次函数y=x2,y=(x-3)2和y=(x+2)2采用如下列表、描点、连线的方式,画出了它们的图像.思考:
1.将下表补充完整:2.从形状上看,二次函数y=(x-3)2,y=(x+2)2的图像与二次函数y=x2的图像的形状和位置有什么关系?(形状相同,位置不同.)3.y=(x-3)2的图像可以由y=x2的图像沿什么方向平移多少个单位长度得到?(沿x轴向右平移3个单位长度得到.)4.y=(x+2)2的图像可以由y=x2的图像沿什么方向平移多少个单位长度得到?(沿x轴向左平移2个单位长度得到.)5.以上三个函数写成y=a(x-h)2的形式,你能类比函数y=ax2的性质归纳这类函数的性质吗?6.二次函数y=a(x-h)2的图像可以由y=ax2的图像沿什么方向平移多少个单位长度得到?1.一般地,抛物线y=a(x-h)2有如下性质:向上向下x=hx=h(h,0)(h,0)当xh时,y随x的增大而增大当xh时,y随x的增大而减小有最低点(h,0).当x=h时,y最小=0有最高点(h,0).当x=h时,y最大=0 2.二次函数y=a(x-h)2的图像可以由y=ax2的图像作如下平移得到:当h>0时,向右平移h个单位长度;当h<0时,向左平移|h|个单位长度.一起探究在如图所示的直角坐标系中,已经画出了二次函数y=(x-3)2的图像.(1)请你在该坐标系中再画出二次函数y=(x-3)2+1和y=(x-3)2-3的图像.(2)请写出函数y=(x-3)2+1和y=(x-3)2-3的图像的对称轴与顶点坐标.(3)类比前边探究函数图像的方法,函数y=a(x-h)2+k有哪些性质?(4)试着说明函数y=(x-3)2+1和y=(x-3)2-3的图像可以分别由函数y=x2的图像经过怎样的平移得到?(5)归纳函数y=a(x-h)2+k的图像可以由函数y=ax2的图像作怎样的平移得到?1.二次函数y=a(x-h)2+k的图像和性质:向上向下x=hx=h(h,k)(h,k)当xh时,y随x的增大而增大当xh时,y随x的增大而减小有最低点(h,k).当x=h时,y最小=k有最低点(h,k).当x=h时,y最大=k2.二次函数y=a(x-h)2+k的图像可以由y=ax2的图像作如下平移得到:当h>0时,向右平移h个单位长度;当h<0时,向左平移|h|个单位长度.当k>0时,向上平移k个单位长度;当k<0时,向下平移|k|个单位长度.大家谈谈(1)请说出将二次函数y=-2x2的图像,分别经过怎样的平移,可以得到函数y=-2(x-4)2+6和y=-2 -4的图像.
(2)指出函数y=-2(x-4)2+6和y=-2 -4的图像的对称轴与顶点坐标,并说明是如何确定的.归纳结论:
1.归纳函数y=a(x-h)2+k的图像是由函数y=x2的图像怎样平移得到的?2.完成下列表格:(教材第34页例1)(1)求函数y=- (x+5)2-2的最大(或最小)值.
(2)先将函数y=- x2的图像向左平移2个单位长度,再向下平移3个单位长度,请写出平移后得到的图像的函数表达式.解:(1)由- <0,知该函数有最大值.
当x=-5时,函数取得最大值,y最大=-2.(2)平移后得到的图像的函数表达式为y=- (x+2)2-3.[知识拓展]1.二次函数y=a(x-h)2,y=a(x-h)2+k的图像和性质综合列表如下:2.二次函数y=a(x-h)2+k的形式叫做二次函数的顶点式,其图像的顶点坐标是(h,k),对称轴是直线x=h.3.把y=ax2的图像向左(或右)平移|h|个单位长度,再向上(或下)平移|k|个单位长度,可以得到函数y=a(x-h)2+k的图像,一般依据“左加右减、上加下减”的原则.检测反馈1.对于二次函数y=(x-2)2+3的图像,下列说法正确的是 ( )
A.开口向下 B.对称轴是x=-1
C.顶点坐标是(2,3) D.与x轴有两个交点解析:二次函数的图像开口向上,所以A错误;对称轴为直线x=2,所以B错误;顶点坐标为(2,3),所以C正确;根据函数图像可得,抛物线与x轴没有交点,所以D错误.故选C.C2.将二次函数y=x2的图像向右平移1个单位长度,再向上平移2个单位长度后,所得图像的函数表达式是 ( )
A.y=(x-1)2+2 B.y=(x+1)2+2 C.y=(x-1)2-2 D.y=(x+1)2-2解析:抛物线y=x2的顶点坐标为(0,0),将该点向右平移1个单位长度,再向上平移2个单位长度得点的坐标为(1,2),所以所得图像的函数表达式为y=(x-1)2+2.故选A.A3.如图所示,在平面直角坐标系中,抛物线所表示的函数表达式为y=-2(x-h)2+k,则下列结论正确的
是 ( )
A.h>0,k>0 B.h<0,k>0
C.h<0,k<0 D.h>0,k<0解析:抛物线y=-2(x-h)2+k的顶点坐标为(h,k),观察图像得顶点在第一象限,所以h>0,k>0.故选A.A4.抛物线y=-3(x-2)2的开口向 ,对称轴是 .?解析:∵a=-3<0,∴抛物线的开口向下.∵抛物线y=a(x-h)2的对称轴是x=h,∴对称轴是直线x=2.x=2下解析:根据平移的规律可得平移后抛物线的解析为y=-3(x+3)2,平移前后的图像形状相同,平移后抛物线的顶点坐标为(-3,0),所以当x=-3时,y有最大值,是0.5.抛物线y=-3x2向左平移3个单位长度后的表达式为 ,它们的形状 ,当x= 时,y有最 值,是 .?y=-3( x+3)2相同-3大0
1.将下表补充完整:2.从形状上看,二次函数y=(x-3)2,y=(x+2)2的图像与二次函数y=x2的图像的形状和位置有什么关系?(形状相同,位置不同.)3.y=(x-3)2的图像可以由y=x2的图像沿什么方向平移多少个单位长度得到?(沿x轴向右平移3个单位长度得到.)4.y=(x+2)2的图像可以由y=x2的图像沿什么方向平移多少个单位长度得到?(沿x轴向左平移2个单位长度得到.)5.以上三个函数写成y=a(x-h)2的形式,你能类比函数y=ax2的性质归纳这类函数的性质吗?6.二次函数y=a(x-h)2的图像可以由y=ax2的图像沿什么方向平移多少个单位长度得到?1.一般地,抛物线y=a(x-h)2有如下性质:向上向下x=hx=h(h,0)(h,0)当x
(2)指出函数y=-2(x-4)2+6和y=-2 -4的图像的对称轴与顶点坐标,并说明是如何确定的.归纳结论:
1.归纳函数y=a(x-h)2+k的图像是由函数y=x2的图像怎样平移得到的?2.完成下列表格:(教材第34页例1)(1)求函数y=- (x+5)2-2的最大(或最小)值.
(2)先将函数y=- x2的图像向左平移2个单位长度,再向下平移3个单位长度,请写出平移后得到的图像的函数表达式.解:(1)由- <0,知该函数有最大值.
当x=-5时,函数取得最大值,y最大=-2.(2)平移后得到的图像的函数表达式为y=- (x+2)2-3.[知识拓展]1.二次函数y=a(x-h)2,y=a(x-h)2+k的图像和性质综合列表如下:2.二次函数y=a(x-h)2+k的形式叫做二次函数的顶点式,其图像的顶点坐标是(h,k),对称轴是直线x=h.3.把y=ax2的图像向左(或右)平移|h|个单位长度,再向上(或下)平移|k|个单位长度,可以得到函数y=a(x-h)2+k的图像,一般依据“左加右减、上加下减”的原则.检测反馈1.对于二次函数y=(x-2)2+3的图像,下列说法正确的是 ( )
A.开口向下 B.对称轴是x=-1
C.顶点坐标是(2,3) D.与x轴有两个交点解析:二次函数的图像开口向上,所以A错误;对称轴为直线x=2,所以B错误;顶点坐标为(2,3),所以C正确;根据函数图像可得,抛物线与x轴没有交点,所以D错误.故选C.C2.将二次函数y=x2的图像向右平移1个单位长度,再向上平移2个单位长度后,所得图像的函数表达式是 ( )
A.y=(x-1)2+2 B.y=(x+1)2+2 C.y=(x-1)2-2 D.y=(x+1)2-2解析:抛物线y=x2的顶点坐标为(0,0),将该点向右平移1个单位长度,再向上平移2个单位长度得点的坐标为(1,2),所以所得图像的函数表达式为y=(x-1)2+2.故选A.A3.如图所示,在平面直角坐标系中,抛物线所表示的函数表达式为y=-2(x-h)2+k,则下列结论正确的
是 ( )
A.h>0,k>0 B.h<0,k>0
C.h<0,k<0 D.h>0,k<0解析:抛物线y=-2(x-h)2+k的顶点坐标为(h,k),观察图像得顶点在第一象限,所以h>0,k>0.故选A.A4.抛物线y=-3(x-2)2的开口向 ,对称轴是 .?解析:∵a=-3<0,∴抛物线的开口向下.∵抛物线y=a(x-h)2的对称轴是x=h,∴对称轴是直线x=2.x=2下解析:根据平移的规律可得平移后抛物线的解析为y=-3(x+3)2,平移前后的图像形状相同,平移后抛物线的顶点坐标为(-3,0),所以当x=-3时,y有最大值,是0.5.抛物线y=-3x2向左平移3个单位长度后的表达式为 ,它们的形状 ,当x= 时,y有最 值,是 .?y=-3( x+3)2相同-3大0
