【冀教版】2017年春九下数学:30.2《二次函数的图象和性质(3)》课件
文档属性
| 名称 | 【冀教版】2017年春九下数学:30.2《二次函数的图象和性质(3)》课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-07 13:33:30 | ||
图片预览





文档简介
课件12张PPT。九年级数学·下 新课标[冀教]第三十章 二次函数30.2 二次函数的图象和性质(第3课时) 在一场足球比赛中,一名球员从球门正前方10米处起脚射门,当球飞行的水平距离为6米时达到最高点,此时球距地面的高度为3米.
(1)如图所示,建立直角坐标系,当球飞行的路线为抛物线时,求此抛物线的表达式;
(2)已知球门高为2.44米,则此球能否射中球门(不计其他情况).共同探究【思考1】(1)你能说出函数y=(x-1)2-2的图像的开口方向、对称轴、顶点坐标、最值及增减性吗?
(2)函数y=(x-1)2-2的图像与函数y=x2的图像有什么关系?
(3)你能将二次函数y=x2-2x-1化成顶点式吗?
(4)不画二次函数的图像,你能直接说出函数y=x2-2x-1的图像的开口方向、对称轴和顶点坐标吗?【思考2】 (1)对于二次函数y=2x2-4x+6,你能化成顶点式吗?
(2)用同样的方法,将二次函数y=ax2+bx+c化成顶点式.其中, ,做一做【思考1】 你能说出二次函数y=ax2+bx+c(a≠0)的图像的形状、开口方向、对称轴、顶点坐标和最值吗?二次函数y=ax2+bx+c的图像是一条抛物线,它的对称轴是 .
若a>0 ,则抛物线开口向上,顶点坐标是( , ).当x<- 时,y随x的增大而减小;当x>- 时,y随x的增大而增大;当x=- 时,y取得最小值,且y最小= ;若a<0 ,则抛物线开口向下,顶点坐标是( , ).当x<- 时,y随x的增大而增大;当x>- 时,y随x的增大而减小;当x=- 时,y取得最大值,且y最大= .【思考2】
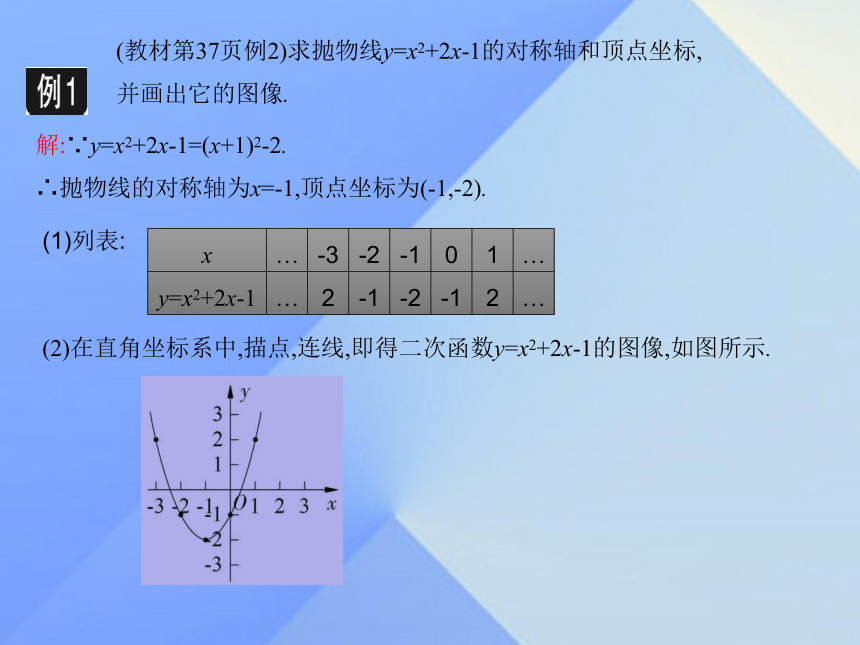
填写下列表格:(教材第37页例2)求抛物线y=x2+2x-1的对称轴和顶点坐标,并画出它的图像.解:∵y=x2+2x-1=(x+1)2-2.
∴抛物线的对称轴为x=-1,顶点坐标为(-1,-2).(1)列表:(2)在直角坐标系中,描点,连线,即得二次函数y=x2+2x-1的图像,如图所示.(教材第37页例3)根据下列条件,确定抛物线的表达式.
(1)抛物线y=-2x2+px+q的顶点坐标为(-3,5).
(2)抛物线y=ax2+bx-6经过点A(-1,3)和B(2,-6).引导:(1)抛物线y=-2x2+px+q配方化成顶点式为 ,根据顶点坐标为(-3,5)可列方程 ,解得p= ,q= ,代入表达式可得 .?
(2)由点A(-1,3)和B(2,-6)的坐标满足抛物线的表达式可得 ,解得a= ,
b= ,代入表达式可得 .?解:(1)∵y=-2x2+px+q= .∴ , =5,
∴p=-12,q=-13.故该抛物线的表达式为y=-2x2-12x-13.(2)点A(-1,3)和B(2,-6)的坐标满足抛物线的表达式,即解得故该抛物线的表达式为y=3x2-6x-6.4.平移法,其步骤如下:
(1)利用配方法把二次函数y=ax2+bx+c化成y=a(x-h)2+k的形式,确定其顶点坐标为(h,k);
(2)画出函数y=ax2的图像;
(3)将函数y=ax2的图像平移,使其顶点平移到(h,k)的位置.[知识拓展] 1.由于抛物线是轴对称图形,且对称轴经过抛物线的顶点,所以抛物线上对称点连线的垂直平分线是对称轴,对称轴与抛物线的交点是顶点.2.在求一般形式的二次函数的图像的对称轴及顶点坐标时,通常有两种方法:一是先将其配方,化y=ax2+bx+c为y=a(x-h)2+k的形式,;二是直接利用公式求顶点坐标.3.若抛物线与x轴有交点,则最好选取交点进行描点,特别是在画抛物线的草图时,应注意以下五点:开口方向、对称轴、顶点、与x轴的交点、与y轴的交点.1.利用配方法将二次函数的一般式化为顶点式:
二次函数y=ax2+bx+c配方,得y=课堂小结2.二次函数y=ax2+bx+c的图像的画法:配方法找到对称轴后对称取点,描点,连线.3.二次函数y=ax2+bx+c的性质:4.待定系数法求函数的表达式.1.将二次函数y=x2-2x+3化为y=a(x-h)2+k的形式,结果为 ( )
A.y=(x+1)2+4 B.y=(x+1)2+2
C.y=(x-1)2+4 D.y=(x-1)2+2解析:y=x2-2x+3=x2-2x+1+2=(x-1)2+2.故选D.D解析:因为y=-x2+4x-4=-(x2-4x+4)=-(x-2)2,所以顶点坐标为(2,0),又a=-1<0,所以当x=2时,y有最大值0.故选B.2.抛物线y=-x2+4x-4 的最值是 ( )
A.当x=-2时,y有最大值0
B.当x=2时,y有最大值0
C.当x=-2时,y有最小值0
D.当x=2时,y有最小值0B3.函数y=-x2-4x-3的图像的顶点坐标是 .?解析:因为y=-x2-4x-3=-(x2+4x+4-4)-3=-(x+2)2+1,所以顶点坐标为(-2,1).故填(-2,1).(-2,1)4.二次函数y=x2+bx+3的图像的对称轴是x=2,则 b= .?解析:由二次函数的图像的对称轴是 =2,解得b=-4.故填-4.-45.已知二次函数y=- x2+x+4.
(1)确定抛物线的开口方向、顶点坐标和对称轴;
(2)当x取何值时,y随x的增大而增大?当x取何值时,y随x的增大而减小?解:∵(1)y=- x2+x+4=- (x-1)2+ ,
∴抛物线的开口向下,顶点坐标为 ,对称轴是x=1.
(2)当x<1时,y随x的增大而增大;当x>1时,y随x的增大而减小.
(1)如图所示,建立直角坐标系,当球飞行的路线为抛物线时,求此抛物线的表达式;
(2)已知球门高为2.44米,则此球能否射中球门(不计其他情况).共同探究【思考1】(1)你能说出函数y=(x-1)2-2的图像的开口方向、对称轴、顶点坐标、最值及增减性吗?
(2)函数y=(x-1)2-2的图像与函数y=x2的图像有什么关系?
(3)你能将二次函数y=x2-2x-1化成顶点式吗?
(4)不画二次函数的图像,你能直接说出函数y=x2-2x-1的图像的开口方向、对称轴和顶点坐标吗?【思考2】 (1)对于二次函数y=2x2-4x+6,你能化成顶点式吗?
(2)用同样的方法,将二次函数y=ax2+bx+c化成顶点式.其中, ,做一做【思考1】 你能说出二次函数y=ax2+bx+c(a≠0)的图像的形状、开口方向、对称轴、顶点坐标和最值吗?二次函数y=ax2+bx+c的图像是一条抛物线,它的对称轴是 .
若a>0 ,则抛物线开口向上,顶点坐标是( , ).当x<- 时,y随x的增大而减小;当x>- 时,y随x的增大而增大;当x=- 时,y取得最小值,且y最小= ;若a<0 ,则抛物线开口向下,顶点坐标是( , ).当x<- 时,y随x的增大而增大;当x>- 时,y随x的增大而减小;当x=- 时,y取得最大值,且y最大= .【思考2】
填写下列表格:(教材第37页例2)求抛物线y=x2+2x-1的对称轴和顶点坐标,并画出它的图像.解:∵y=x2+2x-1=(x+1)2-2.
∴抛物线的对称轴为x=-1,顶点坐标为(-1,-2).(1)列表:(2)在直角坐标系中,描点,连线,即得二次函数y=x2+2x-1的图像,如图所示.(教材第37页例3)根据下列条件,确定抛物线的表达式.
(1)抛物线y=-2x2+px+q的顶点坐标为(-3,5).
(2)抛物线y=ax2+bx-6经过点A(-1,3)和B(2,-6).引导:(1)抛物线y=-2x2+px+q配方化成顶点式为 ,根据顶点坐标为(-3,5)可列方程 ,解得p= ,q= ,代入表达式可得 .?
(2)由点A(-1,3)和B(2,-6)的坐标满足抛物线的表达式可得 ,解得a= ,
b= ,代入表达式可得 .?解:(1)∵y=-2x2+px+q= .∴ , =5,
∴p=-12,q=-13.故该抛物线的表达式为y=-2x2-12x-13.(2)点A(-1,3)和B(2,-6)的坐标满足抛物线的表达式,即解得故该抛物线的表达式为y=3x2-6x-6.4.平移法,其步骤如下:
(1)利用配方法把二次函数y=ax2+bx+c化成y=a(x-h)2+k的形式,确定其顶点坐标为(h,k);
(2)画出函数y=ax2的图像;
(3)将函数y=ax2的图像平移,使其顶点平移到(h,k)的位置.[知识拓展] 1.由于抛物线是轴对称图形,且对称轴经过抛物线的顶点,所以抛物线上对称点连线的垂直平分线是对称轴,对称轴与抛物线的交点是顶点.2.在求一般形式的二次函数的图像的对称轴及顶点坐标时,通常有两种方法:一是先将其配方,化y=ax2+bx+c为y=a(x-h)2+k的形式,;二是直接利用公式求顶点坐标.3.若抛物线与x轴有交点,则最好选取交点进行描点,特别是在画抛物线的草图时,应注意以下五点:开口方向、对称轴、顶点、与x轴的交点、与y轴的交点.1.利用配方法将二次函数的一般式化为顶点式:
二次函数y=ax2+bx+c配方,得y=课堂小结2.二次函数y=ax2+bx+c的图像的画法:配方法找到对称轴后对称取点,描点,连线.3.二次函数y=ax2+bx+c的性质:4.待定系数法求函数的表达式.1.将二次函数y=x2-2x+3化为y=a(x-h)2+k的形式,结果为 ( )
A.y=(x+1)2+4 B.y=(x+1)2+2
C.y=(x-1)2+4 D.y=(x-1)2+2解析:y=x2-2x+3=x2-2x+1+2=(x-1)2+2.故选D.D解析:因为y=-x2+4x-4=-(x2-4x+4)=-(x-2)2,所以顶点坐标为(2,0),又a=-1<0,所以当x=2时,y有最大值0.故选B.2.抛物线y=-x2+4x-4 的最值是 ( )
A.当x=-2时,y有最大值0
B.当x=2时,y有最大值0
C.当x=-2时,y有最小值0
D.当x=2时,y有最小值0B3.函数y=-x2-4x-3的图像的顶点坐标是 .?解析:因为y=-x2-4x-3=-(x2+4x+4-4)-3=-(x+2)2+1,所以顶点坐标为(-2,1).故填(-2,1).(-2,1)4.二次函数y=x2+bx+3的图像的对称轴是x=2,则 b= .?解析:由二次函数的图像的对称轴是 =2,解得b=-4.故填-4.-45.已知二次函数y=- x2+x+4.
(1)确定抛物线的开口方向、顶点坐标和对称轴;
(2)当x取何值时,y随x的增大而增大?当x取何值时,y随x的增大而减小?解:∵(1)y=- x2+x+4=- (x-1)2+ ,
∴抛物线的开口向下,顶点坐标为 ,对称轴是x=1.
(2)当x<1时,y随x的增大而增大;当x>1时,y随x的增大而减小.
