【冀教版】2017年春九下数学:30.3《由不共线三点的坐标确定二次函数》课件
文档属性
| 名称 | 【冀教版】2017年春九下数学:30.3《由不共线三点的坐标确定二次函数》课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-07 00:00:00 | ||
图片预览



文档简介
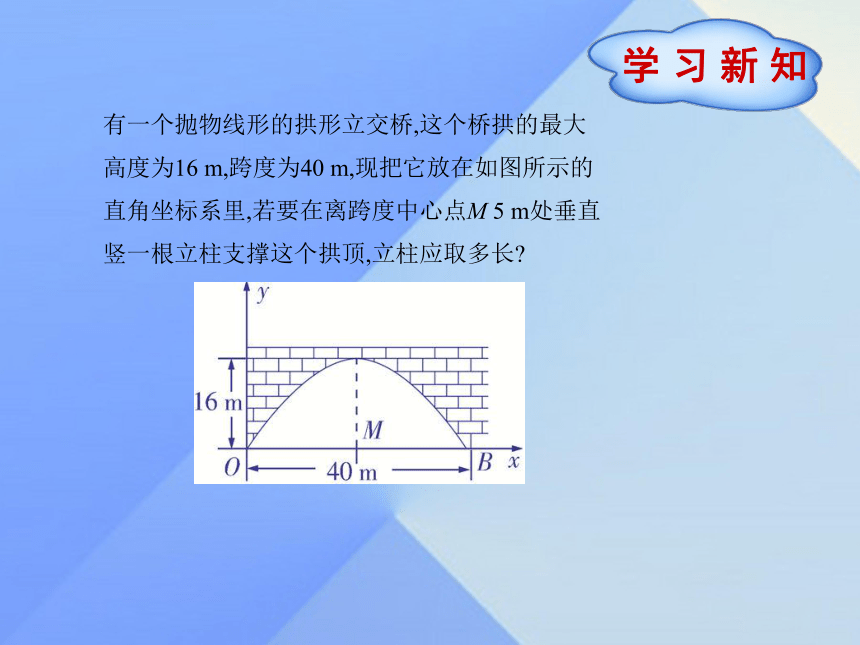
课件9张PPT。九年级数学·下 新课标[冀教]第三十章 二次函数30.3 由不共线三点的坐标确定二次函数有一个抛物线形的拱形立交桥,这个桥拱的最大高度为16 m,跨度为40 m,现把它放在如图所示的直角坐标系里,若要在离跨度中心点M 5 m处垂直竖一根立柱支撑这个拱顶,立柱应取多长?共同探究已知不共线的三点A(1,3),B(2,-2),C(-1,1),怎样确定过这三点的二次函数的表达式呢?共同探究.
1.一次函数y=kx+b中有 个待定系数,需要 个点的坐标代入可以求解.?
2.二次函数y=ax2+bx+c中有 个待定系数,需要 个点的坐标代入可以求解.?
3.已知二次函数的图像经过三点,有三个独立条件,所以可设二次函数表达式为 ;?
4.将三点坐标代入得方程组 ;?
5.解这个方程组得 .?
所以所求的函数表达式为 .?解:设所求的二次函数表达式为y=ax2+bx+c.
将A,B,C三点的坐标分别代入二次函数中,得解得所求二次函数的表达式为y=-2x2+x+4.(教材第39页例)已知三点A(0, 1),B(1, 0),C(2, 3),求由这三点所确定的二次函数表达式.解:设所求二次函数为y=ax2+bx+c.将A,B,C三点的坐标分别代入二次函数表达式中,得 解得所求二次函数的表达式为y=2x2-3x+1.(补充)已知抛物线的顶点坐标为(2,-4),且与y轴交于点(0,3),求这个二次函数表达式.引导:二次函数的顶点式为 ,顶点坐标为 ,?
抛物线顶点为(2,-4)的二次函数表达式可设为 ,?
点(0,3)在抛物线上,所以点的坐标满足函数表达式,所以将点(0,3)代入得 ,
解得 ,所以所求函数表达式为 .?解:设所求二次函数为y=a(x-2)2-4.
由已知得函数图像经过点(0,3),所以4a-4=3.解得a= .
所求二次函数表达式为y= (x-2)2-4,即y= x2-7x+3.1.在直角坐标系中,已知点 ,求由A,B,C三点所确定的二次函数表达式.做一做3.你能解决课前导入中的实际问题吗?2.已知当x=1时,二次函数有最大值5,且图像过点(0,-3),求此函数表达式.解:由题意,知抛物线的顶点坐标为(20,16),
∴可设抛物线的关系式为y=a(x-20)2+16.∵点B(40,0)在抛物线上,
∴0=a(40-20)2+16,
∴a=- . ∴y=- (x-20)2+16.∵竖立柱的点为(15,0)或(25,0),
∴当x=15时,y=- ×(15-20)2+16=15;
当x=25时,y=- ×(25-20)2+16=15.
∴立柱应取15 m.1.(2016·甘肃中考)二次函数y=x2-2x+4化为y=a(x-h)2+k的形式,下列正确的是 ( )
A.y=(x+1)2+2 B.y=(x-1)2+3
C.y=(x-2)2+2 D.y=(x-2)2+4解析:在二次函数的顶点式y=a(x-h)2+k中,h=- =1,k= =3.故选B.B2.(2016·河南中考)已知A(0,3),B(2,3)是抛物线y=-x2+bx+c上两点,该抛物线的顶点坐标是 .?解析:∵A(0,3),B(2,3)是抛物线y=-x2+bx+c上两点,∴代入得 解得b=2,c=3,∴y=-x2+2x+3=-(x-1)2+4,顶点坐标为(1,4).故填(1,4).(1,4)3.已知二次函数y=ax2+bx+c的图像过A(0,-5),B(5,0)两点,它的对称轴为直线x=2,那么这个二次函数的表达式是 .?解析:设二次函数表达式为y=ax2+bx+c,因为过A,B两点,将(0,-5),(5,0)代入,得 又 =2,解得a=1,b=-4,c=-5,所以所求的表达式为y=x2-4x-5.故填y=x2-4x-5.y=x2-4x-5解: 设此二次函数的表达式为y=a(x-1)2+4,
∵其图像经过点(-2,-5),
∴a(-2-1)2+4=-5,
∴a=-1,
∴所求的二次函数的表达式为y=-(x-1)2+4=-x2+2x+3.4.已知二次函数的图像的顶点坐标为(1,4),且其图像经过点(-2,-5),求此二次函数的表达式.
1.一次函数y=kx+b中有 个待定系数,需要 个点的坐标代入可以求解.?
2.二次函数y=ax2+bx+c中有 个待定系数,需要 个点的坐标代入可以求解.?
3.已知二次函数的图像经过三点,有三个独立条件,所以可设二次函数表达式为 ;?
4.将三点坐标代入得方程组 ;?
5.解这个方程组得 .?
所以所求的函数表达式为 .?解:设所求的二次函数表达式为y=ax2+bx+c.
将A,B,C三点的坐标分别代入二次函数中,得解得所求二次函数的表达式为y=-2x2+x+4.(教材第39页例)已知三点A(0, 1),B(1, 0),C(2, 3),求由这三点所确定的二次函数表达式.解:设所求二次函数为y=ax2+bx+c.将A,B,C三点的坐标分别代入二次函数表达式中,得 解得所求二次函数的表达式为y=2x2-3x+1.(补充)已知抛物线的顶点坐标为(2,-4),且与y轴交于点(0,3),求这个二次函数表达式.引导:二次函数的顶点式为 ,顶点坐标为 ,?
抛物线顶点为(2,-4)的二次函数表达式可设为 ,?
点(0,3)在抛物线上,所以点的坐标满足函数表达式,所以将点(0,3)代入得 ,
解得 ,所以所求函数表达式为 .?解:设所求二次函数为y=a(x-2)2-4.
由已知得函数图像经过点(0,3),所以4a-4=3.解得a= .
所求二次函数表达式为y= (x-2)2-4,即y= x2-7x+3.1.在直角坐标系中,已知点 ,求由A,B,C三点所确定的二次函数表达式.做一做3.你能解决课前导入中的实际问题吗?2.已知当x=1时,二次函数有最大值5,且图像过点(0,-3),求此函数表达式.解:由题意,知抛物线的顶点坐标为(20,16),
∴可设抛物线的关系式为y=a(x-20)2+16.∵点B(40,0)在抛物线上,
∴0=a(40-20)2+16,
∴a=- . ∴y=- (x-20)2+16.∵竖立柱的点为(15,0)或(25,0),
∴当x=15时,y=- ×(15-20)2+16=15;
当x=25时,y=- ×(25-20)2+16=15.
∴立柱应取15 m.1.(2016·甘肃中考)二次函数y=x2-2x+4化为y=a(x-h)2+k的形式,下列正确的是 ( )
A.y=(x+1)2+2 B.y=(x-1)2+3
C.y=(x-2)2+2 D.y=(x-2)2+4解析:在二次函数的顶点式y=a(x-h)2+k中,h=- =1,k= =3.故选B.B2.(2016·河南中考)已知A(0,3),B(2,3)是抛物线y=-x2+bx+c上两点,该抛物线的顶点坐标是 .?解析:∵A(0,3),B(2,3)是抛物线y=-x2+bx+c上两点,∴代入得 解得b=2,c=3,∴y=-x2+2x+3=-(x-1)2+4,顶点坐标为(1,4).故填(1,4).(1,4)3.已知二次函数y=ax2+bx+c的图像过A(0,-5),B(5,0)两点,它的对称轴为直线x=2,那么这个二次函数的表达式是 .?解析:设二次函数表达式为y=ax2+bx+c,因为过A,B两点,将(0,-5),(5,0)代入,得 又 =2,解得a=1,b=-4,c=-5,所以所求的表达式为y=x2-4x-5.故填y=x2-4x-5.y=x2-4x-5解: 设此二次函数的表达式为y=a(x-1)2+4,
∵其图像经过点(-2,-5),
∴a(-2-1)2+4=-5,
∴a=-1,
∴所求的二次函数的表达式为y=-(x-1)2+4=-x2+2x+3.4.已知二次函数的图像的顶点坐标为(1,4),且其图像经过点(-2,-5),求此二次函数的表达式.
