【冀教版】2017年春九下数学:30.4《二次函数的应用(1)》课件
文档属性
| 名称 | 【冀教版】2017年春九下数学:30.4《二次函数的应用(1)》课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-07 00:00:00 | ||
图片预览



文档简介
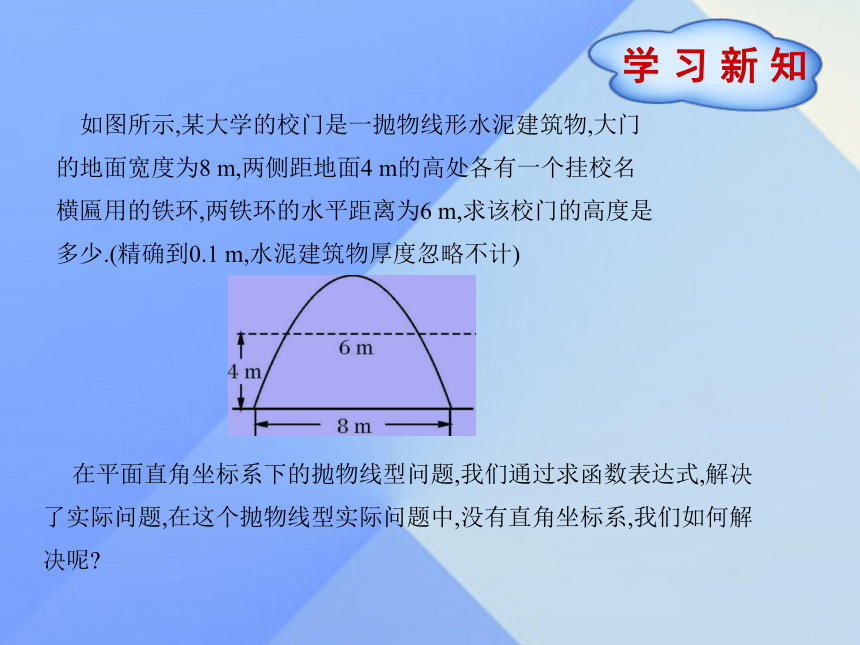
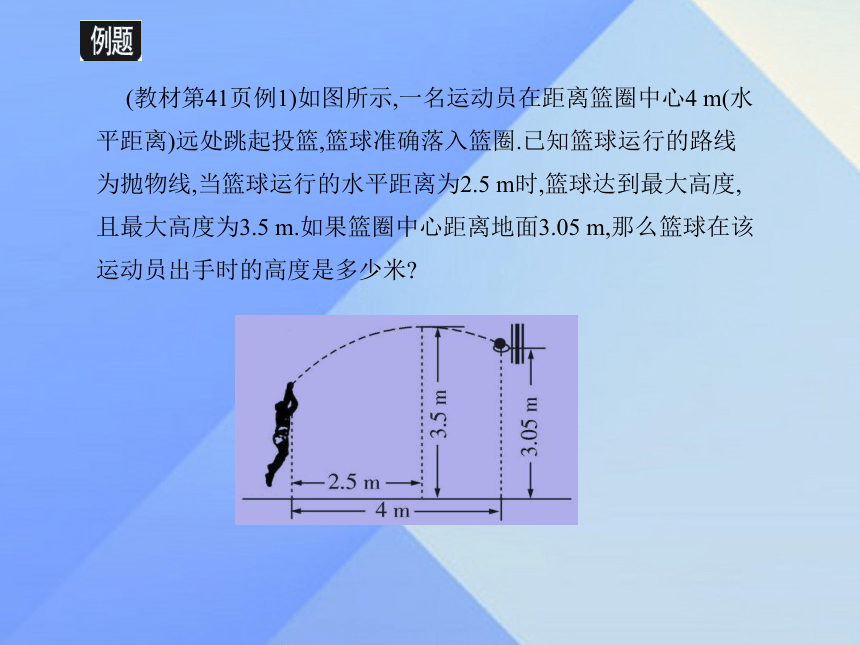
课件10张PPT。九年级数学·下 新课标[冀教]第三十章 二次函数30.4 二次函数的应用(第1课时) 如图所示,某大学的校门是一抛物线形水泥建筑物,大门的地面宽度为8 m,两侧距地面4 m的高处各有一个挂校名横匾用的铁环,两铁环的水平距离为6 m,求该校门的高度是多少.(精确到0.1 m,水泥建筑物厚度忽略不计) 在平面直角坐标系下的抛物线型问题,我们通过求函数表达式,解决了实际问题,在这个抛物线型实际问题中,没有直角坐标系,我们如何解决呢? (教材第41页例1)如图所示,一名运动员在距离篮圈中心4 m(水平距离)远处跳起投篮,篮球准确落入篮圈.已知篮球运行的路线为抛物线,当篮球运行的水平距离为2.5 m时,篮球达到最大高度,且最大高度为3.5 m.如果篮圈中心距离地面3.05 m,那么篮球在该运动员出手时的高度是多少米?思考:
1.如何建立平面直角坐标系?
2.在所建立的平面直角坐标系下如何求二次函数表达式?
3.运动员出手的点在所建的平面直角坐标系下的横坐标是多少?
4.你能求出运动员出手的点的纵坐标吗?解:如图所示,建立直角坐标系,篮圈中心为点A (1.5,3.05),篮球在最大高度时的位置为点B(0,3.5).以点C表示运动员投篮球的出手处.设以y轴(直线x=0)为对称轴的抛物线为y=a(x-0)2+k,即y=ax2+k,而点A,B在这条抛物线上,所以有 解得所以抛物线的表达式为y=-0.2x2+3.5.
当x=-2.5时,y=-0.2×(-2.5)2+3.5=2.25.
答:篮球在该运动员出手时的高度为2.25 m.做一做如图所示,某喷灌器AB的喷头高出地面1.35 m,喷出的水流呈抛物线形从高1 m的小树CD上面的点E处飞过,点C距点A 4.4 m,点E在直线CD上,且距点D 0.35 m,水流最后落在距点A 5.4 m远的点F处.喷出的水流最高处距地面多少米?分析:水流最高处到地面的距离即为抛物线顶点到地面的距离.为求抛物线的表达式,小亮和小惠分别建立了如图(1)(2)所示的直角坐标系,并写出了相关点的坐标.(1)(2)(1)请分别按小亮和小惠建立的直角坐标系求这条抛物线的表达式;
(2)根据以上两种表达式,求出水流最高处到地面的距离.解:如图所示,设抛物线的表达式为y=ax2+k,将点(2.2,1.35),(3.2,0)代入可得:解得所以抛物线的表达式为当x=0时,答:水流最高处到地面的距离为 m.追问: 解决与抛物线有关的实际问题的一般方法是什么?(1)当问题中抛物线在平面直角坐标系中时,合理地设出函数表达式,用待定系数法求出函数表达式,根据二次函数图像和性质解决实际问题;(2)当问题中抛物线不在平面直角坐标系中时,常建立适当的平面直角坐标系,根据题意求出抛物线上点的坐标,用待定系数法求出二次函数表达式,再根据二次函数图像和性质解决问题.练习如图所示,某大学的校门是一抛物线形水泥建筑物,大门的地面宽度为8 m,两侧距地面4 m的高处各有一个挂校名横匾用的铁环,两铁环的水平距离为6 m,求该校门的高度是多少.(精确到0.1 m,水泥建筑物厚度忽略不计)解:以地面为x轴,大门左边与地面的交点为原点建立平面直角坐标系,则抛物线过(0,0),(8,0),(1,4),(7,4)四点,设该抛物线的表达式为y=ax2+bx+c,由题意得到方程组解得∴该抛物线的表达式为y=- x2+ x,顶点坐标为 , ≈9.1.
答:校门的高约为9.1 m.1.汽车刹车距离s(m)与速度v(km/h)之间的函数关系是s= v2,一辆车速为100 km/h的汽车,刹车距离是 ( )
A.1 m B.10 m C. 100 m D.200 m解析:汽车刹车距离s(m)与速度v(km/h)之间的函数关系是s= v2,当v=100时,s=100.故选C.C2.教练对小明推铅球的录像进行技术分析,如图所示,发现铅球行进高度y(m)与水平距离x(m)之间的关系为y= (x-4)2+3,由此可知铅球推出的距离是 m.? 解析:由题意得铅球着地的距离即是二次函数的图像与x轴正半轴的交点的横坐标,所以使 (x-4)2+3=0,解得x=10.故填10. 103.如图所示,有一座抛物线形拱桥,桥下面在正常水位时AB宽20 m,水位上升3 m就达到警戒线CD,这时水面宽度为10 m.
(1)在如图所示的坐标系中求抛物线的表达式;
(2)若洪水到来时,水位以每小时0.2 m的速度上升,从警戒线开始,再持续多少小时才能到拱桥顶?解:(1)设所求抛物线的表达式为y=ax2(a≠0),
由CD=10 m,可设D(5,m),
由AB=20 m,水位上升3 m就达到警戒线CD,则B(10,m-3),
把D,B的坐标分别代入y=ax2得:解得(2)由(1)知m=-1,
∴拱桥顶O到CD的距离为1 m,
∴ =5(小时).
∴再持续5小时到达拱桥顶.
1.如何建立平面直角坐标系?
2.在所建立的平面直角坐标系下如何求二次函数表达式?
3.运动员出手的点在所建的平面直角坐标系下的横坐标是多少?
4.你能求出运动员出手的点的纵坐标吗?解:如图所示,建立直角坐标系,篮圈中心为点A (1.5,3.05),篮球在最大高度时的位置为点B(0,3.5).以点C表示运动员投篮球的出手处.设以y轴(直线x=0)为对称轴的抛物线为y=a(x-0)2+k,即y=ax2+k,而点A,B在这条抛物线上,所以有 解得所以抛物线的表达式为y=-0.2x2+3.5.
当x=-2.5时,y=-0.2×(-2.5)2+3.5=2.25.
答:篮球在该运动员出手时的高度为2.25 m.做一做如图所示,某喷灌器AB的喷头高出地面1.35 m,喷出的水流呈抛物线形从高1 m的小树CD上面的点E处飞过,点C距点A 4.4 m,点E在直线CD上,且距点D 0.35 m,水流最后落在距点A 5.4 m远的点F处.喷出的水流最高处距地面多少米?分析:水流最高处到地面的距离即为抛物线顶点到地面的距离.为求抛物线的表达式,小亮和小惠分别建立了如图(1)(2)所示的直角坐标系,并写出了相关点的坐标.(1)(2)(1)请分别按小亮和小惠建立的直角坐标系求这条抛物线的表达式;
(2)根据以上两种表达式,求出水流最高处到地面的距离.解:如图所示,设抛物线的表达式为y=ax2+k,将点(2.2,1.35),(3.2,0)代入可得:解得所以抛物线的表达式为当x=0时,答:水流最高处到地面的距离为 m.追问: 解决与抛物线有关的实际问题的一般方法是什么?(1)当问题中抛物线在平面直角坐标系中时,合理地设出函数表达式,用待定系数法求出函数表达式,根据二次函数图像和性质解决实际问题;(2)当问题中抛物线不在平面直角坐标系中时,常建立适当的平面直角坐标系,根据题意求出抛物线上点的坐标,用待定系数法求出二次函数表达式,再根据二次函数图像和性质解决问题.练习如图所示,某大学的校门是一抛物线形水泥建筑物,大门的地面宽度为8 m,两侧距地面4 m的高处各有一个挂校名横匾用的铁环,两铁环的水平距离为6 m,求该校门的高度是多少.(精确到0.1 m,水泥建筑物厚度忽略不计)解:以地面为x轴,大门左边与地面的交点为原点建立平面直角坐标系,则抛物线过(0,0),(8,0),(1,4),(7,4)四点,设该抛物线的表达式为y=ax2+bx+c,由题意得到方程组解得∴该抛物线的表达式为y=- x2+ x,顶点坐标为 , ≈9.1.
答:校门的高约为9.1 m.1.汽车刹车距离s(m)与速度v(km/h)之间的函数关系是s= v2,一辆车速为100 km/h的汽车,刹车距离是 ( )
A.1 m B.10 m C. 100 m D.200 m解析:汽车刹车距离s(m)与速度v(km/h)之间的函数关系是s= v2,当v=100时,s=100.故选C.C2.教练对小明推铅球的录像进行技术分析,如图所示,发现铅球行进高度y(m)与水平距离x(m)之间的关系为y= (x-4)2+3,由此可知铅球推出的距离是 m.? 解析:由题意得铅球着地的距离即是二次函数的图像与x轴正半轴的交点的横坐标,所以使 (x-4)2+3=0,解得x=10.故填10. 103.如图所示,有一座抛物线形拱桥,桥下面在正常水位时AB宽20 m,水位上升3 m就达到警戒线CD,这时水面宽度为10 m.
(1)在如图所示的坐标系中求抛物线的表达式;
(2)若洪水到来时,水位以每小时0.2 m的速度上升,从警戒线开始,再持续多少小时才能到拱桥顶?解:(1)设所求抛物线的表达式为y=ax2(a≠0),
由CD=10 m,可设D(5,m),
由AB=20 m,水位上升3 m就达到警戒线CD,则B(10,m-3),
把D,B的坐标分别代入y=ax2得:解得(2)由(1)知m=-1,
∴拱桥顶O到CD的距离为1 m,
∴ =5(小时).
∴再持续5小时到达拱桥顶.
