【冀教版】2017年春九下数学:30.4《二次函数的应用(3)》课件
文档属性
| 名称 | 【冀教版】2017年春九下数学:30.4《二次函数的应用(3)》课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-07 00:00:00 | ||
图片预览



文档简介
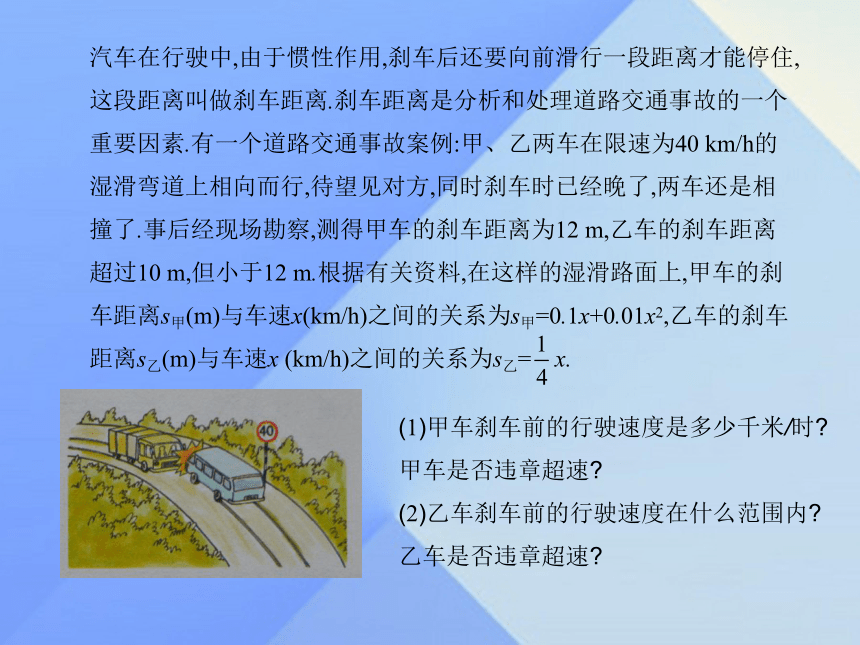
课件8张PPT。九年级数学·下 新课标[冀教]第三十章 二次函数30.4 二次函数的应用(第3课时) 某商品现在的售价为每件60元,每星期可卖出300件.市场调查反映:如调整价格,每涨价1元,每星期要少卖出10件.已知商品的进价是40元,你能写出利润y与售价x之间的函数表达式吗?一星期能获得6125元的利润吗?汽车在行驶中,由于惯性作用,刹车后还要向前滑行一段距离才能停住,这段距离叫做刹车距离.刹车距离是分析和处理道路交通事故的一个重要因素.有一个道路交通事故案例:甲、乙两车在限速为40 km/h的湿滑弯道上相向而行,待望见对方,同时刹车时已经晚了,两车还是相撞了.事后经现场勘察,测得甲车的刹车距离为12 m,乙车的刹车距离超过10 m,但小于12 m.根据有关资料,在这样的湿滑路面上,甲车的刹车距离s甲(m)与车速x(km/h)之间的关系为s甲=0.1x+0.01x2,乙车的刹车距离s乙(m)与车速x (km/h)之间的关系为s乙= x.(1)甲车刹车前的行驶速度是多少千米/时?甲车是否违章超速?
(2)乙车刹车前的行驶速度在什么范围内?乙车是否违章超速?解:(1)将s甲=12代入s甲=0.1x+0.01x2,得
12=0.1x+0.01x2,(1)甲车刹车前的行驶速度是多少千米/时?甲车是否违章超速?化简,得x2+10x-1200=0,
解得x1=30,x2=-40(舍去).
即甲车刹车前的行驶速度为30 km/h,小于40 km/h,不违章超速.(2)∵10∴10< x<12.
∴40∴乙车刹车前的行驶速度在40 km/h~48 km/h,乙车违章超速.(2)乙车刹车前的行驶速度在什么范围内?乙车是否违章超速?追问:
已知二次函数的某个函数值,如何求解对应的自变量的值?已知二次函数y=ax2+bx+c的某一个函数值y=m,就可利用一元二次方程ax2+bx+c=m确定与它对应的x的值. (教材第47页例4) 如图所示,已知边长为1的正方形ABCD,在BC边上有一动点E,连接AE,作EF⊥AE,交CD边于点F.
(1) CF的长可能等于 吗?
(2)点E在什么位置时,CF的长为 ?解:设BE=x,CF=y.
∵∠BAE=∠CEF,
∴Rt△ABE∽Rt△ECF.(1)∵y最大= ,
∴CF的长不可能等于 .(2)设-x2+x= ,即16x2-16x+3=0.
解得x1= ,x2= .
∴当BE的长为 或 时,
均有CF的长为 .1.河北省赵县的赵州桥的桥拱是近似的抛物线形,在如图所示的平面直角坐标系中,其函数的关系式为y=- x2,当水面离桥拱顶的高度DO是4 m时,这时水面宽度AB为 ( )A.-20 m B.10 m
C.20 m D.-10 m解析:根据题意,把y=-4直接代入表达式y=- x2,即可解得x=±10,所以A(-10,-4),B(10,-4),即可得水面宽度AB为20 m.故选C.C2.如图所示的是某地一座抛物线形拱桥,桥拱在竖直平面内,与水平桥面相交于A,B两点,桥拱最高点C到AB的距离为9 m,AB=36 m,D,E为桥拱底部的两点,且DE∥AB,点E到直线AB的距离为7 m,则DE的长为 m. ?解析:如图所示,以点C为原点建立平面直角坐标系,依题意,得B(18,-9),设抛物线的表达式为y=ax2,将B点坐标代入,得a=- .∴抛物线的表达式为y=- x2,依题意得D,E点纵坐标为y=-16,代入y=- x2,得-16=- x2,解得x=±24.∴D点横坐标为-24,E点横坐标为24,∴DE的长为48 m.故填48.483.如图所示,抛物线的表达式为y=-x2+6x,矩形边AB在x轴上,C,D在抛物线上(第一象限).求矩形周长的最大值.解:设OA=m,把x=m代入抛物线y=-x2+6x中,得AD=-m2+6m,
把y=-m2+6m代入抛物线y=-x2+6x中,得-m2+6m=-x2+6x,
解得x1=m,x2=6-m.
∴C的横坐标是6-m,故AB=6-m-m=6-2m,∴矩形的周长是C=2(-m2+6m)+2(6-2m)=-2m2+8m+12.当m=- =2时,C有最大值,为 =20.
∴矩形周长的最大值为20.
(2)乙车刹车前的行驶速度在什么范围内?乙车是否违章超速?解:(1)将s甲=12代入s甲=0.1x+0.01x2,得
12=0.1x+0.01x2,(1)甲车刹车前的行驶速度是多少千米/时?甲车是否违章超速?化简,得x2+10x-1200=0,
解得x1=30,x2=-40(舍去).
即甲车刹车前的行驶速度为30 km/h,小于40 km/h,不违章超速.(2)∵10
∴40
已知二次函数的某个函数值,如何求解对应的自变量的值?已知二次函数y=ax2+bx+c的某一个函数值y=m,就可利用一元二次方程ax2+bx+c=m确定与它对应的x的值. (教材第47页例4) 如图所示,已知边长为1的正方形ABCD,在BC边上有一动点E,连接AE,作EF⊥AE,交CD边于点F.
(1) CF的长可能等于 吗?
(2)点E在什么位置时,CF的长为 ?解:设BE=x,CF=y.
∵∠BAE=∠CEF,
∴Rt△ABE∽Rt△ECF.(1)∵y最大= ,
∴CF的长不可能等于 .(2)设-x2+x= ,即16x2-16x+3=0.
解得x1= ,x2= .
∴当BE的长为 或 时,
均有CF的长为 .1.河北省赵县的赵州桥的桥拱是近似的抛物线形,在如图所示的平面直角坐标系中,其函数的关系式为y=- x2,当水面离桥拱顶的高度DO是4 m时,这时水面宽度AB为 ( )A.-20 m B.10 m
C.20 m D.-10 m解析:根据题意,把y=-4直接代入表达式y=- x2,即可解得x=±10,所以A(-10,-4),B(10,-4),即可得水面宽度AB为20 m.故选C.C2.如图所示的是某地一座抛物线形拱桥,桥拱在竖直平面内,与水平桥面相交于A,B两点,桥拱最高点C到AB的距离为9 m,AB=36 m,D,E为桥拱底部的两点,且DE∥AB,点E到直线AB的距离为7 m,则DE的长为 m. ?解析:如图所示,以点C为原点建立平面直角坐标系,依题意,得B(18,-9),设抛物线的表达式为y=ax2,将B点坐标代入,得a=- .∴抛物线的表达式为y=- x2,依题意得D,E点纵坐标为y=-16,代入y=- x2,得-16=- x2,解得x=±24.∴D点横坐标为-24,E点横坐标为24,∴DE的长为48 m.故填48.483.如图所示,抛物线的表达式为y=-x2+6x,矩形边AB在x轴上,C,D在抛物线上(第一象限).求矩形周长的最大值.解:设OA=m,把x=m代入抛物线y=-x2+6x中,得AD=-m2+6m,
把y=-m2+6m代入抛物线y=-x2+6x中,得-m2+6m=-x2+6x,
解得x1=m,x2=6-m.
∴C的横坐标是6-m,故AB=6-m-m=6-2m,∴矩形的周长是C=2(-m2+6m)+2(6-2m)=-2m2+8m+12.当m=- =2时,C有最大值,为 =20.
∴矩形周长的最大值为20.
